Modelling the Mechanical and Strain Recovery Behaviour of Partially Crystalline PLA
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Small Strain Structural Modelling
3.1.1. Analytical Approach
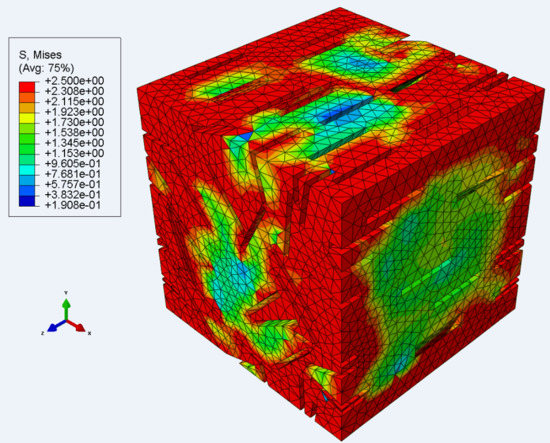
3.1.2. Numerical Approach
3.2. Experimental
3.2.1. Stress–strain Results
3.2.2. Stress Relaxation
3.2.3. Strain Recovery under Load
3.3. Numerical Analysis of Results
3.3.1. Effects of Inclusions
3.3.2. Modelling the Time-Dependent Yield of the Amorphous Phase
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Avérous, L. Biodegradable Multiphase Systems Based on Plasticized Starch: A Review. J. Macromol. Sci. Polym. Rev. 2004, 44, 231–274. [Google Scholar] [CrossRef]
- Castro-Aguirre, E.; Iñiguez-Franco, F.; Samsudin, H.; Fang, X.; Auras, R. Poly(lactic acid)—Mass production, processing, industrial applications, and end of life. Adv. Drug Delivery Rev. 2016, 107, 333–366. [Google Scholar] [CrossRef] [PubMed]
- Athanasiou, K.A.; Niederauer, G.G.; Agrawal, C.M. Sterilization, toxicity, biocompatibility and clinical applications of polylactic acid/polyglycolic acid copolymers. Biomaterials 1996, 17, 93–102. [Google Scholar] [CrossRef]
- Brkaric, M.; Baker, K.C.; Israel, R.; Harding, T.; Montgomery, D.M.; Herkowit, H.N. Early failure of bioabsorbable anterial cerivcal fusion plates. J. Spinal Disord. Tech. 2007, 20, 248–254. [Google Scholar] [CrossRef] [PubMed]
- Smit, T.H.; Engels, T.A.P.; Wuisman, P.I.J.M.; Govaert, L.E. Time-dependent mechanical strength of 70/30 poly(l,dl-lactide): Shedding light on the premature failure of degradable spinal cages. Spine 2008, 33, 14–18. [Google Scholar] [CrossRef]
- Rebelo, R.; Fernandes, M.; Fangueiro, R. Biopolymers in medical implants: A brief review. Procedia Eng. 2017, 200, 236–243. [Google Scholar] [CrossRef]
- Xu, J.; Song, J. Polylactic acid (PLA)-based shape-memory materials for biomedical applications. In Shape Memory Polymers for Biomedical Applications; Woodhead Publishing: Cambridge, UK, 2015; pp. 197–217. [Google Scholar]
- Farah, S.; Anderson, D.G.; Langer, R. Physical and mechanical properties of PLA, and their functions in widespread applications—A comprehensive review. Adv. Drug Delivery Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef]
- Garlotta, D.A. Literature review of Poly(Lactic Acid). J. Polym. Environ. 2001, 9, 63–84. [Google Scholar] [CrossRef]
- Bergström, J.S. Hayman D An Overview of Mechanical Properties and Material Modeling of Polylactide (PLA) for Medical Applications. Ann. Biomed. Eng. 2016, 44, 330–340. [Google Scholar] [CrossRef]
- Al-Itry, R.; Lamnawar, K.; Maazouz, A.; Billon, N.; Combeaud, C. Effect of the simultaneous biaxial stretching on the structural and mechanical properties of PLA, PBAT and their blends at rubbery state. Eur. Polym. J. 2015, 68, 288–301. [Google Scholar] [CrossRef]
- Blair, R.W.; Dunne, N.J.; Lennon, A.B.; Menary, G.H. Processing-property relationships of biaxially stretched poly(l-lactic acid) sheet for application in coronary stents. J. Mech. Behav. Biomed. Mater. 2018, 86, 113–121. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Pan, Y.; Liu, X.; Liu, H.; Li, N.; Liu, C.; Schubert, D.W.; Shen, C. Facile Fabrication of Superhydrophobic and Eco-Friendly Poly(lactic acid) Foam for Oil−Water Separation via Skin Peeling. ACS Appl. Mater. Interfaces 2019, 11, 14362–14367. [Google Scholar] [CrossRef] [PubMed]
- Chacón, J.M.; Caminero, M.A.; García-Plaza, M.; Núnez, P.J. Additive manufacturing of PLA structures using fused deposition modelling: Effect of process parameters on mechanical properties and their optimal selection. Mater. Des. 2017, 124, 143–157. [Google Scholar] [CrossRef]
- Coates, P.D.; Ward, I.M. Drawing of Polymers through a Conical Die. Polymer 1979, 20, 1553–1560. [Google Scholar] [CrossRef]
- Coates, P.D.; Ward, I.M. Die Drawing—Solid-Phase Drawing of Polymers through a Converging Die. Polym. Eng. Sci. 1981, 21, 612–618. [Google Scholar]
- Ward, I.M.; Taraiya, A.K.; Coates, P.D. Solid state extrusion and die drawing. In Solid Phase Processing of Polymers; Hanser: Munich, Germany, 2000; pp. 328–365. [Google Scholar]
- Li, J.; Li, Z.; Ye, L.; Zhao, X.; Coates, P.D.; Caton-Rose, F. Structure evolution and orientation mechanism of long-chain-branched poly(lactic acid) in the process of solid die drawing. Eur. Polym. J. 2017, 90, 54–65. [Google Scholar] [CrossRef]
- Li, J.; Li, Z.; Ye, L.; Zhao, X.; Coates, P.D.; Caton-Rose, F. Structure and biocompatibility improvement mechanism of highly oriented poly(lactic acid) produced by solid die drawing. Eur. Polym. J. 2017, 90, 68–76. [Google Scholar] [CrossRef]
- Vasile, C.; Stoleru, E.; Darie-Niţa, R.N.; Dumitriu, R.P.; Pamfil, D.; Tarţau, R. Biocompatible Materials Based on Plasticized Poly(lactic acid), Chitosan and Rosemary Ethanolic Extract I. Effect of Chitosan on the Properties of Plasticized Poly(lactic acid) Materials. Polymers 2019, 11, 941. [Google Scholar] [CrossRef]
- Li, Q.; Liu, C.; Wena, J.; Wua, Y.; Shana, Y.; Liao, J. The design, mechanism and biomedical application of self-healing hydrogels. Chin. Chem. Lett. 2017, 28, 1857–1874. [Google Scholar] [CrossRef]
- Ye, A.; Wang, S.; Zhao, Q.; Wang, Y.; Liu, C.; Shen, C. Poly(ethylene oxide)-promoted dispersion of graphene nanoplatelets and its effect on the properties of poly(lactic acid)/poly(butylene adipate-co-terephthalate)-based nanocomposites. Mater. Lett. 2019, 253, 34–37. [Google Scholar] [CrossRef]
- Peponi, L.; Navarro-Baena, I.; Kenny, J.M. Shape memory polymers: Properties, synthesis and applications. In Smart Polymers and Their Applications; Aguilar, M.R., Román, J.S., Eds.; Woodhead Publishing in Materials, Elsevier: Cambridge, UK, 2014; pp. 204–236. [Google Scholar]
- Fillon, T.M.; Xu, J.; Prasad, M.L.; Song, J. In Vivo Tissue Responses to Thermal-responsive Shape Memory Polymer Nanocomposites. Biomaterials 2011, 32, 985–991. [Google Scholar] [CrossRef]
- Walzac, J.; Sobota, M.; Chrzanowski, M.; Krucinska, I. Application of the melt-blown technique in the production of shape-memory nonwoven fabrics from a blend of poly(l-lactide) and atactic poly[(R,S)-3-hydroxy butyrate]. Text. Res. J. 2018, 88, 2141–2152. [Google Scholar]
- Zhang, H.; Wang, S.; Zhang, S.; Ma, R.; Wang, Y.; Cao, W.; Liu, C.; Shen, C. Crystallization behavior of poly(lactic acid) with a self-assembly aryl amide nucleating agent probed by real-time infrared spectroscopy and X-ray diffraction. Polym. Test. 2017, 64, 12–19. [Google Scholar] [CrossRef]
- Peltoniemi, H.; Kontio, R.; Lindqvist, C.; Suuronen, R. The use of bioabsorbable osteofixation devices in craniomaxillofacial surgery. Oral Surg. Oral Med. Oral Pathol. 2002, 84, 5–14. [Google Scholar] [CrossRef]
- Halpin, J.C.; Kardos, J.L. Moduli of crystalline polymers employing composite theory. J. Appl. Phys. 1972, 43, 2235–2241. [Google Scholar] [CrossRef]
- Halpin, J.C.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar]
- Kong, Y.; Hay, J.N. The measurement of crystallinity of polymers with DSC. Polymer 2002, 3873–3878. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Tucker, C.L.; Liang, E. Stiffness predictions for unidirectional short-fiber composites: Review and evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Spencer, M.W.; Paul, D.R. Modeling the mechanical and thermal expansion behavior of TPO-based nanocomposites. Polymer 2011, 52, 4910–4919. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids, 2nd ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991; pp. 77–84. [Google Scholar]
- Lee, S.; Kimoto, M.; Tanaka, M.; Tsuji, H.; Nishino, T. Crystal modulus of poly(lactic acid)s, and their stereocomplex. Polymer 2018, 138, 124–131. [Google Scholar] [CrossRef]
- Tábi, T.; Sajó, I.E.; Szabó, F.; Luyt, A.S.; Kovács, J.G. Crystalline structure of annealed polylactic acid and its relation to processing. Express Polym. Lett. 2010, 10, 659–668. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes, the Art of Scientific Computing. Cambridge University Press: London, UK, 1986. [Google Scholar]
- Söntjens, S.H.M.; Engels, T.A.P.; Smit, T.H.; Govaert, L.E. Time-dependent failure of amorphous poly-d,l-lactide: Influence of molecular weight. J. Mech. Behav. Biomed. Mater. 2012, 13, 69–77. [Google Scholar] [CrossRef]
- Zhou, C.; Guo, H.; Li, J.; Huang, S.; Li, H.; Meng, Y.; Yu, D.; de Claville Christiansen, J.; Jiang, S. Temperature dependence of poly(lactic acid) mechanical properties. RSC Adv. 2016, 6, 113762–113772. [Google Scholar] [CrossRef]
- Guedes, R.M.; Singh, A.; Pinto, V. Viscoelastic Modelling of Creep and Stress Relaxation Behaviour in PLA-PCL Fibres. Fibers Polym. 2017, 18, 2443–2453. [Google Scholar] [CrossRef]
- Dusunceli, N.; Drozdov, A.D.; Theilgaard, N. Influence of Temperature on Viscoelastic–Viscoplastic Behavior of Poly(lactic acid) Under Loading–Unloading. Polym. Eng. Sci. 2017, 57, 239–247. [Google Scholar] [CrossRef]
- Sweeney, J.; Bonner, M.; Ward, I.M. Modelling of loading, stress relaxation and stress recovery of a shape memory polymer. J. Mech. Behav. Biomed. Mater. 2014, 37, 12–23. [Google Scholar] [CrossRef]
- Tcharkhtchi, A.; Abdallah-Elhirsti, S.; Ebrahimi, K.; Fitoussi, J.; Shirinbayan, M.; Farzaneh, S. Some New Concepts of Shape Memory Effect of Polymers. Polymers 2014, 6, 1144–1163. [Google Scholar] [CrossRef] [Green Version]
- Ward, I.M.; Sweeney, J. Mechanical Properties of Solid Polymers, 3rd ed.; Wiley: Chichester, UK, 2013. [Google Scholar]
- Halsey, G.; White, H.J.; Eyring, H. Mechanical properties of textiles, I. Text. Res. J. 1945, 15, 295–311. [Google Scholar] [CrossRef]
- Guiu, F.; Pratt, P.L. Stress relaxation and the plastic deformation of solids. Phys. Status Solidi. 1964, 6, 111–120. [Google Scholar] [CrossRef]











| Aspect Ratio d/w | N target Number of Inclusions | Number of Realisations | Mean Modulus (GPa) | |
|---|---|---|---|---|
| 0.086 | 87 | 11 | 0.667 | 0.534 ± 0.017 |
| 0.086 | 87 | 12 | 1.0 | 0.523 ± 0.022 |
| 0.17 | 43 | 21 | 0.667 | 0.512 ± 0.035 |
| 0.34 | 22 | 21 | 0.667 | 0.507 ± 0.029 |
| p | |
|---|---|
| 1.0 | 0.140 |
| 2.5 | 0.134 |
| 5.0 | 0.139 |
| 10.0 | 0.156 |
| Arm | V (MPa)−1 | α (s−1) | G (MPa) |
|---|---|---|---|
| q | 0.45 | 0.004 | 120 |
| r | 2.2 | 1.0 × 10−6 | 0.74 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sweeney, J.; Spencer, P.; Nair, K.; Coates, P. Modelling the Mechanical and Strain Recovery Behaviour of Partially Crystalline PLA. Polymers 2019, 11, 1342. https://doi.org/10.3390/polym11081342
Sweeney J, Spencer P, Nair K, Coates P. Modelling the Mechanical and Strain Recovery Behaviour of Partially Crystalline PLA. Polymers. 2019; 11(8):1342. https://doi.org/10.3390/polym11081342
Chicago/Turabian StyleSweeney, John, Paul Spencer, Karthik Nair, and Phil Coates. 2019. "Modelling the Mechanical and Strain Recovery Behaviour of Partially Crystalline PLA" Polymers 11, no. 8: 1342. https://doi.org/10.3390/polym11081342
APA StyleSweeney, J., Spencer, P., Nair, K., & Coates, P. (2019). Modelling the Mechanical and Strain Recovery Behaviour of Partially Crystalline PLA. Polymers, 11(8), 1342. https://doi.org/10.3390/polym11081342