New Spectrophotometric Method for Quantitative Characterization of Density-Driven Convective Instability
Abstract
:1. Introduction
2. Experimental
2.1. Experimental Setup
2.2. Material and Properties
2.3. Experimental Procedure
3. Theory and Methods
3.1. Dimensionless Parameters
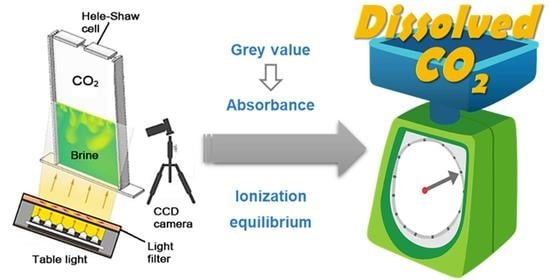
3.2. Spectrophotometric Method
3.3. Numerical Simulation
4. Results and Discussion
4.1. Development Regimes and Morphology of Instabilities
4.2. Effects of Brine Salinity and Temperature
4.3. Determination of the Mass of Dissolved CO2
4.4. Comparison between Experimental and Simulation Results
5. Conclusions
- There are three different regimes of instability development: diffusion dissolution regime, convection diffusion regime, and shutdown regime. The course and development of the convective fingers go through generation, propagation, coalescence, and re-initiation.
- Brine salinity has a negative effect on the CO2 convective dissolution. Thus, with increases in salinity, the convection starting time delay, the length of fingers, and fingers growth rate decrease.
- Although increasing the temperature causes an increase in the diffusion coefficient, the solubility of CO2 in water decreases the density difference. An increase in temperature leads to a reduction in the initial wave number and CO2 affected area, which can adversely affect CO2 dissolution.
- The spectrophotometric method was successfully used to quantitatively measure the dissolved CO2 concentration. The mass of dissolved CO2 due to convective dissolution is much greater than that for diffusion dissolution. The dimensionless flux, where the Sherwood number shows a power-law relationship with the Rayleigh number, indicates that the Sh increases with increasing Ra, and this refers to the lower salinity and temperature increasing the mass transfer flux of CO2 dissolution.
- Salinity and temperature effects on convective instability of numerical simulation are in qualitative agreement with the experimental result. The shape and position of the convective finger in the simulation are influenced by the assumption of boundary conditions. Numerical simulation of CO2 convective dissolution still requires further research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Montzka, S.A.; Dlugokencky, E.J.; Butler, J.H. Non-CO2 greenhouse gases and climate change. Nature 2011, 476, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Miocic, J.M.; Gilfillan, S.M.V.; Frank, N.; Schroeder-Ritzrau, A.; Burnside, N.M.; Haszeldine, R.S. 420,000 year assessment of fault leakage rates shows geological carbon storage is secure. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Bachu, S.; Adams, J. Sequestration of CO2 in geological media in response to climate change: Capacity of deep saline aquifers to sequester CO2 in solution. Energy Convers. Manag. 2003, 44, 3151–3175. [Google Scholar] [CrossRef]
- Hassanzadeh, H.; Pooladi-Darvish, M.; Keith, D.W. Accelerating CO2 dissolution in saline aquifers for geological storage Mechanistic and sensitivity studies. Energy Fuels 2009, 23, 3328–3336. [Google Scholar] [CrossRef]
- Thomas, C.; Lemaigre, L.; Zalts, A.; D’Onofrio, A.; De Wit, A. Experimental study of CO2 convective dissolution: The effect of color indicators. Int. J. Greenh. Gas Control 2015, 42, 525–533. [Google Scholar] [CrossRef]
- Kneafsey, T.J.; Pruess, K. Laboratory Flow Experiments for Visualizing Carbon Dioxide-Induced, Density-Driven Brine Convection. Transp. Porous Media 2009, 82, 123–139. [Google Scholar] [CrossRef] [Green Version]
- Mahmoodpour, S.; Rostami, B.; Soltanian, M.R.; Amooie, M.A.J. Convective dissolution of carbon dioxide in deep saline aquifers: Insights from engineering a high-pressure porous Hele-Shaw cell. arXiv 2018, arXiv:1812.08366. [Google Scholar] [CrossRef] [Green Version]
- Outeda, R.; El Hasi, C.; D’Onofrio, A.; Zalts, A. Experimental study of linear and nonlinear regimes of density-driven instabilities induced by CO2 dissolution in water. Chaos Interdiscip. J. Nonlinear Sci. 2014, 24, 013135. [Google Scholar] [CrossRef] [Green Version]
- Oldenburg, C.M.; Rinaldi, A.P. Buoyancy Effects on Upward Brine Displacement Caused by CO2 Injection. Transp. Porous Media 2010, 87, 525–540. [Google Scholar] [CrossRef] [Green Version]
- Trémosa, J.; Castillo, C.; Vong, C.Q.; Kervévan, C.; Lassin, A.; Audigane, P. Long-term assessment of geochemical reactivity of CO2 storage in highly saline aquifers: Application to Ketzin, In Salah and Snøhvit storage sites. Int. J. Greenh. Gas Control 2014, 20, 2–26. [Google Scholar] [CrossRef] [Green Version]
- Bachu, S. Screening and ranking of sedimentary basins for sequestration of CO2 in geological media in response to climate change. Environ. Geol. 2003, 44, 277–289. [Google Scholar] [CrossRef]
- Bachu, S.; Bennion, B. Effects of in-situ conditions on relative permeability characteristics of CO2-brine systems. Environ. Geol. 2007, 54, 1707–1722. [Google Scholar] [CrossRef]
- Alkan, H.; Cinar, Y.; Ülker, E.B. Impact of Capillary Pressure, Salinity and In Situ Conditions on CO2 Injection into Saline Aquifers. Transp. Porous Media 2010, 84, 799–819. [Google Scholar] [CrossRef]
- Lindeberg, E.; Wessel-Berg, D. Vertical convection in an aquifer column under a gas cap of CO2. Energy Convers. Manag. 1997, 38, S229–S234. [Google Scholar] [CrossRef]
- Raad, S.M.; Hassanzadeh, H. Onset of dissolution-driven instabilities in fluids with nonmonotonic density profile. Phys. Rev. E 2015, 92, 053023. [Google Scholar] [CrossRef]
- Trevelyan, P.M.J.; Almarcha, C.; De Wit, A. Buoyancy-driven instabilities of miscible two-layer stratifications in porous media and Hele-Shaw cells. J. Fluid Mech. 2011, 670, 38–65. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.; Chen, S.; Zhang, D. Convective stability analysis of the long-term storage of carbon dioxide in deep saline aquifers. Adv. Water Resour. 2006, 29, 397–407. [Google Scholar] [CrossRef]
- Nakanishi, Y.; Hyodo, A.; Wang, L.; Suekane, T. Experimental study of 3D Rayleigh–Taylor convection between miscible fluids in a porous medium. Adv. Water Resour. 2016, 97, 224–232. [Google Scholar] [CrossRef]
- Wang, L.; Nakanishi, Y.; Hyodo, A.; Suekane, T. Three-dimensional structure of natural convection in a porous medium: Effect of dispersion on finger structure. Int. J. Greenh. Gas Control 2016, 53, 274–283. [Google Scholar] [CrossRef]
- Arendt, B.; Dittmar, D.; Eggers, R. Interaction of interfacial convection and mass transfer effects in the system CO2–water. Int. J. Heat Mass Transf. 2004, 47, 3649–3657. [Google Scholar] [CrossRef]
- Mojtaba, S.; Behzad, R.; Rasoul, N.M.; Mohammad, R. Experimental study of density-driven convection effects on CO2 dissolution rate in formation water for geological storage. J. Nat. Gas Sci. Eng. 2014, 21, 600–607. [Google Scholar] [CrossRef]
- And, C.Y.; Gu, Y. Accelerated Mass Transfer of CO2 in Reservoir Brine Due to Density-Driven Natural Convection at High Pressures and Elevated Temperatures. Ind. Eng. Chem. Res. 2005, 45, 2430–2436. [Google Scholar]
- Shi, Z.; Wen, B.; Hesse, M.; Tsotsis, T.; Jessen, K.J.A. Measurement and modeling of CO2 mass transfer in brine at reservoir conditions. Adv. Water Resour. 2018, 113, 100–111. [Google Scholar] [CrossRef]
- Amir, T.; Ole, T.; Mansour, S. Experimental and simulation studies of density-driven-convection mixing in a Hele-Shaw geometry with application for CO sequestration in brine aquifers. Investig. Bibliotecol. 2012, 26, 233–247. [Google Scholar]
- Faisal, T.F.; Chevalier, S.; Bernabe, Y.; Juanes, R.; Sassi, M. Quantitative and qualitative study of density driven CO2 mass transfer in a vertical Hele-Shaw cell. Int. J. Heat Mass Transf. 2015, 81, 901–914. [Google Scholar] [CrossRef]
- Liyanage, R.; Crawshaw, J.; Krevor, S.; Pini, R.J.E.P. Multidimensional Imaging of Density Driven Convection in a Porous Medium. Energy Procedia 2017, 114, 4981–4985. [Google Scholar] [CrossRef]
- Teng, Y.; Jiang, L.; Fan, Y.; Liu, Y.; Wang, D.; Abudula, A.; Song, Y. Quantifying the dynamic density driven convection in high permeability packed beds. Magn. Reson. Imaging 2017, 39, 168–174. [Google Scholar] [CrossRef] [PubMed]
- Neufeld, J.A.; Hesse, M.A.; Riaz, A.; Hallworth, M.A.; Tchelepi, H.A.; Huppert, H.E. Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, S.; Abudula, A.; Liu, Y.; Song, Y. The effect of density difference on the development of density-driven convection under large Rayleigh number. Int. J. Heat Mass Transf. 2019, 139, 1087–1095. [Google Scholar] [CrossRef]
- Slim, A.C.; Bandi, M.M.; Miller, J.C.; Mahadevan, L. Dissolution-driven convection in a Hele–Shaw cell. Phys. Fluids 2013, 25, 024101. [Google Scholar] [CrossRef] [Green Version]
- Backhaus, S.; Turitsyn, K.; Ecke, R.E. Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 2011, 106, 104501. [Google Scholar] [CrossRef] [Green Version]
- Jafari Raad, S.M.; Emami-Meybodi, H.; Hassanzadeh, H. On the choice of analogue fluids in CO2 convective dissolution experiments. Water Resour. Res. 2016, 52, 4458–4468. [Google Scholar] [CrossRef]
- Sun, T.; Teja, A.S. Density, viscosity and thermal conductivity of aqueous solutions of propylene glycol, dipropylene glycol, and tripropylene glycol between 290 K and 460 K. J. Chem. 2004, 49, 1311–1317. [Google Scholar] [CrossRef]
- Tsai, P.A.; Riesing, K.; Stone, H.A. Density-driven convection enhanced by an inclined boundary: Implications for geological CO2 storage. Phys. Rev. E 2013, 87, 011003. [Google Scholar] [CrossRef] [Green Version]
- Rasmusson, M.; Fagerlund, F.; Rasmusson, K.; Tsang, Y.; Niemi, A. Refractive-Light-Transmission Technique Applied to Density-Driven Convective Mixing in Porous Media with Implications for Geological CO2 Storage. Water Resour. Res. 2017, 53, 8760–8780. [Google Scholar] [CrossRef]
- Nordbotten, J.M.; Celia, M.A.; Bachu, S. Injection and Storage of CO2 in Deep Saline Aquifers: Analytical Solution for CO2 Plume Evolution During Injection. Transp. Porous Media 2005, 58, 339–360. [Google Scholar] [CrossRef]
- Rasmusson, M.; Fagerlund, F.; Tsang, Y.; Rasmusson, K.; Niemi, A. Prerequisites for density-driven instabilities and convective mixing under broad geological CO2 storage conditions. Adv. Water Resour. 2015, 84, 136–151. [Google Scholar] [CrossRef]
- Watson, M.N.; Zwingmann, N.; Lemon, N.M. The Ladbroke Grove–Katnook carbon dioxide natural laboratory: A recent CO2 accumulation in a lithic sandstone reservoir. Energy 2004, 29, 1457–1466. [Google Scholar] [CrossRef]
- Duan, Z.; Hu, J.; Li, D.; Mao, S. Densities of the CO2–H2O and CO2–H2O–NaCl Systems Up to 647 K and 100 MPa. Energy Fuels 2008, 22, 1666–1674. [Google Scholar] [CrossRef]
- Unver, A.A.; Himmelblau, D.M. Diffusion Coefficients of CO2, C2H4, C3H6 and C4H8 in Water from 6 to 65 °C. J. Chem. Eng. Data 1964, 9, 428–431. [Google Scholar] [CrossRef]
- Ingle, J.D., Jr.; Crouch, S.R. Spectrochemical Analysis; Pearson College Div: New York, NY, USA, 1988. [Google Scholar]
- Rasband, W. ImageJ; US National Institutes of Health: Bethesda, MD, USA, 1997. [Google Scholar]
- Harned, H.S.; Davis, R., Jr. The ionization constant of carbonic acid in water and the solubility of carbon dioxide in water and aqueous salt solutions from 0 to 50. J. Am. Chem. Soc. 1943, 65, 2030–2037. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Luckner, L.; Van Genuchten, M.T.; Nielsen, D.R. A consistent set of parametric models for the two-phase flow of immiscible fluids in the subsurface. Water Resour. Res. 1989, 25, 2187–2193. [Google Scholar] [CrossRef]
- White, M.D.; Bacon, D.H.; McGrail, B.P.; Watson, D.J.; White, S.K.; Zhang, Z. STOMP Subsurface Transport Over Multiple Phases: STOMP-CO2 and STOMP-CO2e Guide: Version 1.0; Pacific Northwest National Lab (PNNL): Richland, WA, USA, 2012. [Google Scholar]
- Emami-Meybodi, H.; Hassanzadeh, H. Two-phase convective mixing under a buoyant plume of CO2 in deep saline aquifers. Adv. Water Resour. 2015, 76, 55–71. [Google Scholar] [CrossRef]
- Sainz-Garcia, A.; Abarca, E.; Nardi, A.; Grandia, F.; Oelkers, E.H. Convective mixing fingers and chemistry interaction in carbon storage. Int. J. Greenh. Gas Control 2017, 58, 52–61. [Google Scholar] [CrossRef] [Green Version]
- Pruess, K.; Spycher, N. ECO2N—A fluid property module for the TOUGH2 code for studies of CO2 storage in saline aquifers. Energy Convers. Manag. 2007, 48, 1761–1767. [Google Scholar] [CrossRef]
- Yan, W.; Huang, S.; Stenby, E.H. Measurement and modeling of CO2 solubility in NaCl brine and CO2–saturated NaCl brine density. Int. J. Greenh. Gas Control 2011, 5, 1460–1477. [Google Scholar] [CrossRef]
- Garcia, J.E. Density of Aqueous Solutions of CO2; Report LBNL-49023; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2001. [Google Scholar]
- Anderson, G.M.; Crerar, D.A. Thermodynamics in Geochemistry: The Equilibrium Model; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Duan, Z.; Sun, R. An improved model calculating CO2 solubility in pure water and aqueous NaCl solutions from 273 to 533 K and from 0 to 2000 bar. Chem. Geol. 2003, 193, 257–271. [Google Scholar] [CrossRef]
- Taheri, A.; Lindeberg, E.; Torsæter, O.; Wessel-Berg, D. Qualitative and quantitative experimental study of convective mixing process during storage of CO2 in homogeneous saline aquifers. Int. J. Greenh. Gas Control 2017, 66, 159–176. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Meulenbroek, B.; Daniel, D.; Riaz, A.; Bruining, J.J.C.G. An empirical theory for gravitationally unstable flow in porous media. Comput. Geosci. 2013, 17, 515–527. [Google Scholar] [CrossRef]
















| No. | Temperature (°C) | Salinity (mg/L) | ∆ρ (kg/m3) | Viscosity (kg/m s) | Diffusion Coefficient (m2/s) | Rayleigh Number |
|---|---|---|---|---|---|---|
| 1 | 25 | 0 | 0.37 | 9.13 × 10−4 | 1.85 × 10−9 | 17,406.23 |
| 2 | 25 | 5000 | 0.36 | 9.27 × 10−4 | 1.85 × 10−9 | 17,143.36 |
| 3 | 25 | 10,000 | 0.35 | 9.42 × 10−4 | 1.85 × 10−9 | 16,401.75 |
| 4 | 25 | 15,000 | 0.34 | 1.03 × 10−3 | 1.85 × 10−9 | 15,362.34 |
| 5 | 35 | 0 | 0.25 | 7.08 × 10−4 | 2.18 × 10−9 | 13,228.03 |
| 6 | 45 | 0 | 0.19 | 5.94 × 10−4 | 3.03 × 10−9 | 8621.23 |
| 25 °C | 35 °C | 45 °C | |
|---|---|---|---|
| AHIn | 0.039 | 0.044 | 0.051 |
| AIn- | 0.987 | 0.993 | 1.014 |
| pKHIn | 4.67 | 4.71 | 4.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, Y.; Wang, P.; Jiang, L.; Liu, Y.; Wei, Y. New Spectrophotometric Method for Quantitative Characterization of Density-Driven Convective Instability. Polymers 2021, 13, 661. https://doi.org/10.3390/polym13040661
Teng Y, Wang P, Jiang L, Liu Y, Wei Y. New Spectrophotometric Method for Quantitative Characterization of Density-Driven Convective Instability. Polymers. 2021; 13(4):661. https://doi.org/10.3390/polym13040661
Chicago/Turabian StyleTeng, Ying, Pengfei Wang, Lanlan Jiang, Yu Liu, and Yang Wei. 2021. "New Spectrophotometric Method for Quantitative Characterization of Density-Driven Convective Instability" Polymers 13, no. 4: 661. https://doi.org/10.3390/polym13040661
APA StyleTeng, Y., Wang, P., Jiang, L., Liu, Y., & Wei, Y. (2021). New Spectrophotometric Method for Quantitative Characterization of Density-Driven Convective Instability. Polymers, 13(4), 661. https://doi.org/10.3390/polym13040661