Molecular Dynamics Simulation of Nanocellulose-Stabilized Pickering Emulsions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Molecular Dynamics Simulation
2.2. MesoDyn Coarse-Grained Calculation
3. Results and Discussion
3.1. Formation of Pickering Emulsion with an Excess Supply of Nanocellulose
3.1.1. Thermodynamic Properties with Increasing Nanocellulose Concentration
3.1.2. Effect of Nanocellulose Concentration on the Bead Order
3.1.3. Density Map with Excess Supply of Nanocellulose
3.2. Formation of Pickering Emulsion with Excess Poly-1-Butene
3.2.1. Thermodynamic Properties with Increasing Poly-1-Butene Concentration
3.2.2. Effect of Poly-1-Butene Concentration on Bead Order
3.2.3. Density Map with Excess Supply of Poly-1-Butene
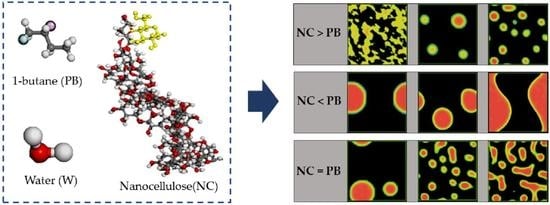
3.3. Effect of Equal Ratio of NC and PB to the System
Effect of Equal Ratio of NC/PB to Free Energy Densities in the System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, M.; Zhang, T.; Zhang, H.; Tao, N.; Wang, X.; Zhong, J. Gelatin molecular structures affect behaviors of fish oil-loaded traditional and Pickering emulsions. Food Chem. 2020, 309, 125642. [Google Scholar] [CrossRef]
- Fujisawa, S.; Togawa, E.; Kuroda, K. Nanocellulose-stabilized Pickering emulsions and their applications. Sci. Technol. Adv. Mater. 2017, 18, 959–971. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.W.; Heo, S.K.; Foo, M.L.; Chew, I.M.L.; Yoo, C.K. An insight into nanocellulose as soft condensed matter: Challenge and future prospective toward environmental sustainability. Sci. Total Environ. 2019, 650, 1309–1326. [Google Scholar] [CrossRef] [PubMed]
- Goodarzi, F.; Zendehboudi, S. A Comprehensive Review on Emulsions and Emulsion Stability in Chemical and Energy Industries. Can. J. Chem. Eng. 2019, 97, 281–309. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.; Liu, X.; Chang, C.; Wang, Y. Recent developments and prospective food-related applications of cellulose nanocrystals: A review. Cellulose 2020, 27, 2991–3011. [Google Scholar] [CrossRef]
- Abushammala, H.; Mao, J. A Review of the Surface Modification of Cellulose and Nanocellulose Using Aliphatic and Aromatic Mono- and Di-Isocyanates. Molecules 2019, 24, 2782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoo, Y.; Youngblood, J.P. Green One-Pot Synthesis of Surface Hydrophobized Cellulose Nanocrystals in Aqueous Medium. ACS Sustain. Chem. Eng. 2016, 4, 3927–3938. [Google Scholar] [CrossRef]
- Yang, X.; Biswas, S.K.; Han, J.; Tanpichai, S.; Li, M.-C.; Chen, C.; Zhu, S.; Das, A.K.; Yano, H. Surface and Interface Engineering for Nanocellulosic Advanced Materials. Adv. Mater. 2020, 2002264, in press. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-Y.; Blaker, J.J.; Murakami, R.; Heng, J.Y.Y.; Bismarck, A. Phase Behavior of Medium and High Internal Phase Water-in-Oil Emulsions Stabilized Solely by Hydrophobized Bacterial Cellulose Nanofibrils. Langmuir 2014, 30, 452–460. [Google Scholar] [CrossRef]
- Clark, G.L.; Parker, E.A. An X-ray Diffraction Study of the Action of Liquid Ammonia on Cellulose and Its Derivatives. J. Phys. Chem. 1937, 41, 777–786. [Google Scholar] [CrossRef]
- Wada, M.; Heux, L.; Sugiyama, J. Polymorphism of Cellulose I Family: Reinvestigation of Cellulose IVI. Biomacromolecules 2004, 5, 1385–1391. [Google Scholar] [CrossRef] [PubMed]
- Medronho, B.; Duarte, H.; Alves, L.; Antunes, F.; Romano, A.; Lindman, B. Probing Cellulose Amphiphilicity. 2015, 30, 58–66. [Google Scholar] [CrossRef] [Green Version]
- French, A.D.; Johnson, G.P. Quantum mechanics studies of cellobiose conformations. Can. J. Chem. 2006, 84, 603–612. [Google Scholar] [CrossRef]
- Mo, Y.; Zhang, H.B.; Xu, J. Molecular dynamic simulation of the mechanical properties of PI/SiO2 nanocomposite based on materials studio. J. Chem. Pharm. Res. 2014, 6, 1534–1539. [Google Scholar]
- Ma, J.; Song, X.; Luo, J.; Zhao, T.; Yu, H.; Peng, B.; Zhao, S. Molecular Dynamics Simulation Insight into Interfacial Stability and Fluidity Properties of Microemulsions. Langmuir 2019, 35, 13636–13645. [Google Scholar] [CrossRef] [PubMed]
- Pirhadi, S.; Amani, A. Molecular dynamics simulation of self-assembly in a nanoemulsion system. Chem. Pap. 2020, 74, 2443–2448. [Google Scholar] [CrossRef]
- Foo, M.L.; Tan, C.R.; Lim, P.D.; Ooi, C.W.; Tan, K.W.; Chew, I.M.L. Surface-modified nanocrystalline cellulose from oil palm empty fruit bunch for effective binding of curcumin. Int. J. Biol. Macromol. 2019, 138, 1064–1071. [Google Scholar] [CrossRef]
- Bahaman, A.H.; Wahab, R.A.; Abdul Hamid, A.A.; Abd Halim, K.B.; Kaya, Y. Molecular docking and molecular dynamics simulations studies on β-glucosidase and xylanase Trichoderma asperellum to predict degradation order of cellulosic components in oil palm leaves for nanocellulose preparation. J. Biomol. Struct. Dyn. 2020, in press. [Google Scholar] [CrossRef]
- Chen, P.; Lo Re, G.; Berglund, L.A.; Wohlert, J. Surface modification effects on nanocellulose-molecular dynamics simulations using umbrella sampling and computational alchemy. J. Mater. Chem. A 2020, 8, 23617–23627. [Google Scholar] [CrossRef]
- Ruiz-Morales, Y.; Mullins, O.C. Coarse-grained molecular simulations to investigate asphaltenes at the oil-water interface. Energy Fuels 2015, 29, 1597–1609. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, X.; Wang, P.; Wang, H.; Wang, Z.; Luo, J.; Li, C.; Hu, S. Emulsified oil phase induced internal instability of ionic and nonionic foams revealed by coarse-grained molecular dynamics simulation. Comput. Mater. Sci. 2019, 169, 109111. [Google Scholar] [CrossRef]
- Paajanen, A.; Vaari, J. High-temperature decomposition of the cellulose molecule: A stochastic molecular dynamics study. Cellulose 2017, 24, 2713–2725. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Tang, C.; Wang, Q.; Li, X.; Hao, J. Selection of Optimal Polymerization Degree and Force Field in the Molecular Dynamics Simulation of Insulating Paper Cellulose. Energies 2017, 10, 1377. [Google Scholar] [CrossRef] [Green Version]
- Heiland, K.; Kaminsky, W. Comparison of zirconocene and hafnocene catalysts for the polymerization of ethylene and 1-butene. Macromol. Chem. Phys. 1992, 193, 601–610. [Google Scholar] [CrossRef]
- Khazraji, A.C.; Robert, S. Interaction Effects between Cellulose and Water in Nanocrystalline and Amorphous Regions: A Novel Approach Using Molecular Modeling. J. Nanomater. 2013, 2013, 409676. [Google Scholar] [CrossRef] [Green Version]
- Ramli, S.; Mohamad, J.S.; Abdul, S.M.A.; Zainuddin, N.; Abdul Rahman, I. Formulation and Physical Characterization of Microemulsions based Carboxymethyl Cellulose as Vitamin C Carrier. Malays. J. Anal. Sci. 2015, 19, 275–283. [Google Scholar]
- Liu, H. Fiber Lubrication: A Molecular Dynamics Simulation Study. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2009. [Google Scholar]
- Wohlert, J.; Berglund, L.A. A Coarse-Grained Model for Molecular Dynamics Simulations of Native Cellulose. J. Chem. Theory Comput. 2011, 7, 753–760. [Google Scholar] [CrossRef]
- Huynh, L.; Grant, J.; Leroux, J.-C.; Delmas, P.; Allen, C. Predicting the Solubility of the Anti-Cancer Agent Docetaxel in Small Molecule Excipients using Computational Methods. Pharm. Res. 2008, 25, 147–157. [Google Scholar] [CrossRef]
- Kaevand, T.; Öpik, A.; Lille, Ü. A Mesoscale Simulation of the Morphology of the PEDT/PSS Complex in the Water Dispersion and Thin Film: The Use of the MesoDyn Simulation Code. In Advances in Computer and Information Sciences and Engineering; Sobh, T., Ed.; Springer: Dordrecht, The Netherlands, 2008; pp. 540–546. [Google Scholar]
- Zhang, B.; Liu, R.; Zhang, J.; Liu, B.; He, J. MesoDyn simulation study of phase behavior for dye–polyether derivatives in aqueous solutions. Comput. Theor. Chem. 2016, 1091, 8–17. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Bao, M.; Chen, Q. Aggregation Behavior of Surfactants with Different Molecular Structures in Aqueous Solution: DPD Simulation Study. J. Dispers. Sci. Technol. 2012, 33, 1437–1443. [Google Scholar] [CrossRef]
- Liu, X.; He, F.; Salas, C.; Pasquinelli, M.A.; Genzer, J.; Rojas, O.J. Experimental and Computational Study of the Effect of Alcohols on the Solution and Adsorption Properties of a Nonionic Symmetric Triblock Copolymer. J. Phys. Chem. B 2012, 116, 1289–1298. [Google Scholar] [CrossRef] [PubMed]
- Slimane, M.; Ghoul, M.; Chebil, L. Mesoscale Modeling Approach to Study the Dispersion and the Solubility of Flavonoids in Organic Solvents. Ind. Eng. Chem. Res. 2018, 57, 12519–12530. [Google Scholar] [CrossRef]
- Maiti, A.; McGrother, S. Bead–bead interaction parameters in dissipative particle dynamics: Relation to bead-size, solubility parameter, and surface tension. J. Chem. Phys. 2004, 120, 1594–1601. [Google Scholar] [CrossRef]
- Alany, R.G.; Wen, J. Microemulsions as Drug Delivery Systems. In Pharmaceutical Manufacturing Handbook; Gad, S.C., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; pp. 769–792. [Google Scholar]
- Mortensen, K.; Pedersen, J.S. Structural study on the micelle formation of poly(ethylene oxide)-poly(propylene oxide)-poly(ethylene oxide) triblock copolymer in aqueous solution. Macromolecules 1993, 26, 805–812. [Google Scholar] [CrossRef]
- Yamane, C.; Aoyagi, T.; Ago, M.; Sato, K.; Okajima, K.; Takahashi, T. Two Different Surface Properties of Regenerated Cellulose due to Structural Anisotropy. Polym. J. 2006, 38, 819–826. [Google Scholar] [CrossRef] [Green Version]
- Dong, S.; Zhang, H.; Cui, X.; Sui, Z.; Xu, J.I.A.; Wang, H. Mesoscopic Simulation on the Phase Structure of Pluronic P105 Aqueous Solution. J. Theor. Comput. Chem. 2010, 9, 767–783. [Google Scholar] [CrossRef]
- Li, Y.; Hou, T.; Guo, S.; Wang, K.; Xu, X. The Mesodyn simulation of pluronic water mixtures using the ‘equivalent chain’ method. Phys. Chem. Chem. Phys. 2000, 2, 2749–2753. [Google Scholar] [CrossRef]
- Ougiya, H.; Watanabe, K.; Morinaga, Y.; Yoshinaga, F. Emulsion-stabilizing Effect of Bacterial Cellulose. Biosci. Biotechnol. Biochem. 1997, 61, 1541–1545. [Google Scholar] [CrossRef] [Green Version]












| Molecule (Bead) | Mp (g/mol) | Mm (g/mol) | Cn | Nmeso | Chain Topology |
|---|---|---|---|---|---|
| Nanocellulose (NC) | 3244.84 | 164.157 | 4.37854927 | 5 | C5 |
| Poly-1-butene | 394.772 | 58.124 | 7.32595465 | 1 | PB1 |
| Water (W) | - | 18.015 | - | 1 | W1 |
| Beads | C | PB | W |
|---|---|---|---|
| C | 0 | - | - |
| PB | 12.2418032 | 0 | - |
| W | 3.8780612 | 13.1866039 | 0 |
| RT = 2477.572 J/mol |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, K.K.; Low, D.Y.S.; Foo, M.L.; Yu, L.J.; Choong, T.S.Y.; Tang, S.Y.; Tan, K.W. Molecular Dynamics Simulation of Nanocellulose-Stabilized Pickering Emulsions. Polymers 2021, 13, 668. https://doi.org/10.3390/polym13040668
Lee KK, Low DYS, Foo ML, Yu LJ, Choong TSY, Tang SY, Tan KW. Molecular Dynamics Simulation of Nanocellulose-Stabilized Pickering Emulsions. Polymers. 2021; 13(4):668. https://doi.org/10.3390/polym13040668
Chicago/Turabian StyleLee, Ka Kit, Darren Yi Sern Low, Mei Ling Foo, Lih Jiun Yu, Thomas Shean Yaw Choong, Siah Ying Tang, and Khang Wei Tan. 2021. "Molecular Dynamics Simulation of Nanocellulose-Stabilized Pickering Emulsions" Polymers 13, no. 4: 668. https://doi.org/10.3390/polym13040668
APA StyleLee, K. K., Low, D. Y. S., Foo, M. L., Yu, L. J., Choong, T. S. Y., Tang, S. Y., & Tan, K. W. (2021). Molecular Dynamics Simulation of Nanocellulose-Stabilized Pickering Emulsions. Polymers, 13(4), 668. https://doi.org/10.3390/polym13040668