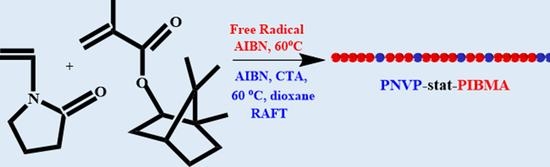
Statistical Copolymers of N-Vinylpyrrolidone and Isobornyl Methacrylate via Free Radical and RAFT Polymerization: Monomer Reactivity Ratios, Thermal Properties, and Kinetics of Thermal Decomposition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Synthesis of PNVP-co-PIBMA Statistical Copolymers via Free Radical and RAFT Polymerization
2.3. Characterization Techniques
3. Results and Discussion
3.1. Statistical Copolymers of NVP and IBMA via Free Radical Polymerization
3.2. Reactivity Ratios
3.3. Statistical Copolymers of NVP and IBMA via RAFT Polymerization
3.4. Thermal Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Odian, G. Principles of Polymerization; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hadjichristidis, N.; Pitsikalis, M.; Pispas, S.; Iatrou, H. Polymers with complex architectures by living anionic polymerization. Chem. Rev. 2001, 101, 3747–3792. [Google Scholar] [CrossRef]
- Hadjichristidis, N.; Pispas, S.; Iatrou, H.; Pitsikalis, M. Linking chemistry and anionic polymerization. Curr. Org. Chem. 2002, 6, 155–176. [Google Scholar] [CrossRef]
- Hadjichristidis, N.; Hirao, A. Anionic Polymerization: Principles, Practice, Strength, Consequences and Applications; Springer: Berlin, Germany, 2015. [Google Scholar]
- Kennedy, J.P. Living cationic polymerization of olefins. How did the discovery come about? J. Polym. Sci. Part A Polym. Chem. 1999, 37, 2285–2293. [Google Scholar] [CrossRef]
- Webster, O.W. The discovery and commercialization of group transfer polymerization. J. Polym. Sci. Part A Polym. Chem. 2000, 38, 2855–2860. [Google Scholar] [CrossRef]
- Leitgeb, A.; Wappel, J.; Slugovc, C. The ROMP toolbox upgraded. Polymer 2010, 51, 2927–2946. [Google Scholar] [CrossRef]
- Matyjaszewski, K.; Davis, T.P. Handbook of Radical Polymerization; Wiley-Interscience: Hoboken, NJ, USA, 2002. [Google Scholar]
- Martin, L.; Gody, G.; Perrier, S. Preparation of complex multiblock copolymers via aqueous RAFT polymerization at room temperature. Polym. Chem. 2015, 6, 4875–4886. [Google Scholar] [CrossRef]
- Boyer, C.; Bulmus, V.; Davis, T.P.; Ladmiral, V.; Liu, J.; Perrier, S. Bioapplications of RAFT Polymerization. Chem. Rev. 2009, 109, 5402–5436. [Google Scholar] [CrossRef]
- Roth, P.J.; Boyer, C.; Lowe, A.B.; Davis, T.P. RAFT Polymerization and Thiol Chemistry: A Complementary Pairing for Implementing Modern Macromolecular Design. Macromol. Rapid Commun. 2011, 32, 1123–1143. [Google Scholar] [CrossRef] [PubMed]
- Perrier, S. 50th Anniversary Perspective: RAFT Polymerization—A User Guide. Macromolecules 2017, 50, 7433–7447. [Google Scholar] [CrossRef]
- Moad, G.; Rizzardo, E.; Thang, S.H. Living Radical Polymerization by the RAFT Process—A Third Update. Aust. J. Chem. 2012, 65, 985–1076. [Google Scholar] [CrossRef]
- Hadjichristidis, N.; Iatrou, H.; Pitsikalis, M.; Pispas, S.; Avgeropoulos, A. Linear and non-linear multiblock terpolymers. Synthesis, self-assembly in selective solvents and in bulk. Progr. Polym. Sci. 2005, 30, 725–782. [Google Scholar] [CrossRef]
- Hadjichristidis, N.; Pitsikalis, M.; Iatrou, H. Synthesis of block copolymers. Adv. Polym. Sci. 2005, 189, 1–124. [Google Scholar]
- Hadjichristidis, N.; Iatrou, H.; Pitsikalis, M.; Mays, J.W. Macromolecular architectures by living and controlled/living polymerizations. Progr. Polym. Sci. 2006, 31, 1068–1132. [Google Scholar] [CrossRef]
- Hadjichristidis, N.; Pitsikalis, M.; Iatrou, H.; Sakellariou, G. Macromolecular Architectures by Living and Controlled/Living Polymerizations in Controlled and Living Polymerizations. From Mechanisms to Applications; Müller, A.H.E., Matyjaszewski, K., Eds.; Wiley VCH: Weinheim, Germany, 2009; Chapter 7; pp. 343–443. [Google Scholar]
- Nielsen, B.V.; Nevell, T.G.; Barbu, E.; Smith, J.R.; Rees, G.D.; Tsibouklis, J. Multifunctional poly(alkyl methacrylate) films for dental care. Biomed. Mater. 2011, 6, 015003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, X.; Li, W.; Zhu, Z.; Han, N.; Zhang, X. Thermo-responsive PVDF/PSMA composite membranes with micro/nanoscale hierarchical structures for oil/water emulsion separation. Colloid Surf. A 2017, 516, 305–316. [Google Scholar] [CrossRef]
- Awasthi, R.; Manchanda, S.; Das, P.; Velu, V.; Malipeddi, H.; Pabreja, K.; Pinto, T.; Gupta, G.; Dua, K. Poly(vinylpyrrolidone). In Engineering of Biomaterials for Drug Delivery Systems; Parambath, A., Ed.; Woodhead Publishing: Cambridge, UK, 2018; Chapter 9; pp. 255–272. [Google Scholar]
- Baraker, B.M.; Lobo, B. Dispersion parameters of cadmium chloride doped PVA-PVP blend films. J. Polym. Res. 2017, 24, 84. [Google Scholar] [CrossRef]
- Karatzas, A.; Bilalis, P.; Iatrou, H.; Pitsikalis, M.; Hadjichristidis, N. Synthesis of well-defined functional macromolecular chimeras based on poly(ethylene oxide) or poly(N-vinyl pyrrolidone). React. Funct. Polym. 2009, 69, 435–440. [Google Scholar] [CrossRef]
- Bilalis, P.; Zorba, G.; Pitsikalis, M.; Hadjichristidis, N. Synthesis of poly(n-hexyl isocyanate-b-N-vinylpyrrolidone) block copolymers by the combination of anionic and nitroxide-mediated radical polymerizations: Micellization properties in aqueous solutions. J. Polym. Sci. Part A Polym. Chem. Ed. 2006, 44, 5719–5728. [Google Scholar] [CrossRef]
- Bilalis, P.; Pitsikalis, M.; Hadjichristidis, N. Controlled nitroxide-mediated and reversible addition-fragmentation chain transfer polymerization of N-vinylpyrrolidone: Synthesis of block copolymers with styrene and 2-vinylpyridine. J. Polym. Sci. Part A Polym. Chem. Ed. 2006, 44, 659–665. [Google Scholar] [CrossRef]
- Ngadaonye, J.I.; Cloonan, M.O.; Geever, L.M.; Higginbotham, C.L. Synthesis and characterisation of thermo-sensitive terpolymer hydrogels for drug delivery applications. J. Polym. Res. 2011, 18, 2307–2324. [Google Scholar] [CrossRef]
- Abd El-Mohdy, H.L.; Ghanem, S. Biodegradability, antimicrobial activity and properties of PVA/PVP hydrogels prepared by γ-irradiation. J. Polym. Res. 2009, 16, 1–10. [Google Scholar] [CrossRef]
- Hadjichristidis, N.; Mays, J.; Ferry, W. Properties and chain flexibility of poly(dl-isobornyl methacrylate). J. Polym. Sci. Part A Polym. Phys. Ed. 1984, 22, 1745–1751. [Google Scholar] [CrossRef]
- Yu, J.M.; Dubois, P.; Jérôme, R. Synthesis and properties of poly[isobornyl methacrylate (IBMA)-b-butadiene (BD)-b-IBMA] copolymers: New thermoplastic elastomers of a large service temperature range. Macromolecules 1996, 29, 7316–7322. [Google Scholar] [CrossRef]
- Métafiot, A.; Gagnon, L.; Pruvost, S.; Hubert, P.; Gérard, J.-F.; Defoort, B.; Marić, M. β-myrcene/isobornyl methacrylate SG1 nitroxide mediated controlled radical polymerization: Synthesis and characterization of gradient, diblock and triblock copolymers. RSC Adv. 2019, 7, 3377–3395. [Google Scholar] [CrossRef] [Green Version]
- Métafiot, A.; Pruvost, S.; Gérard, J.-F.; Defoort, B.; Marić, M. Synthesis of isoprene-based triblock copolymers by nitroxide-mediated polymerization. Eur. Polym. J. 2020, 134, 109798. [Google Scholar] [CrossRef]
- Yu, J.M.; Dubois, P.; Jérôme, R. Poly[poly(isobornyl methacrylate-co-methyl methacrylate) (poly(IBMA-co-MMA))-b-polybutadiene-b-poly(IBMA-co-MMA)] copolymers: Synthesis, morphology, properties. Macromolecules 1997, 30, 6536–6543. [Google Scholar] [CrossRef]
- Hajiali, F.; Métafiot, A.; Benitez-Ek, L.; Alloune, L.; Marić, M. Nitroxide mediated polymerization of sustainably sourced isobornyl methacrylate and tridecyl methacrylate with acrylonitrile co-monomer. J. Polym. Sci. Part A Polym. Chem. 2018, 56, 2422–2436. [Google Scholar] [CrossRef]
- Zaremba, D.; Evert, R.; Neumann, L.; Caspary, R.; Kowalsky, W.; Menzel, H.; Johannes, H.-H. Methacrylate-based copolymers for polymer optical fibers. Polymers 2017, 9, 34. [Google Scholar] [CrossRef] [Green Version]
- Yeh, S.-L.; Zhu, C.-Y.; Kuo, S.-W. Transparent heat-resistant PMMA copolymers for packing light-emitting diode materials. Polymers 2015, 7, 1379–1388. [Google Scholar] [CrossRef] [Green Version]
- Jumeaux, C.; Chapman, R.; Chandrawati, R.; Stevens, M.M. Synthesis and self-assembly of temperature-responsive copolymers based on N-vinylpyrrolidone and triethylene glycol methacrylate. Polym. Chem. 2015, 6, 4116–4122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keddie, D.J.; Guerrero-Sanchez, C.; Moad, G.; Rizzardo, E.; Thang, S.H. Switchable reversible addition-fragmentation chain transfer (RAFT) polymerization in aqueous solution, N,N-dimethylacrylamide. Macromolecules 2011, 44, 6738–6745. [Google Scholar] [CrossRef]
- Moad, G.; Keddie, D.; Guerrero-Sanchez, C.; Rizzardo, E.; Thang, S.H. Advances in switchable RAFT polymerization. Macromol. Symp. 2015, 350, 34–42. [Google Scholar] [CrossRef]
- Stace, S.J.; Moad, G.; Fellows, C.M.; Keddie, D.J. The effect of Z-group modification on the RAFT polymerization of N-vinylpyrrolidone controlled by “switchable” N-pyridyl-functional dithiocarbamates. Polym. Chem. 2015, 6, 7119–7126. [Google Scholar] [CrossRef]
- Hagiopol, C. Copolymerization: Toward a Systematic Approach; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Wan, D.; Satoh, K.; Kamigaito, M.; Okamoto, Y. Xanthate-Mediated Radical Polymerization of N-Vinylpyrrolidone in Fluoroalcohols for Simultaneous Control of Molecular Weight and Tacticity. Macromolecules 2005, 38, 10397–10405. [Google Scholar] [CrossRef]
- Fineman, M.; Ross, S.D. Linear method for determining monomer reactivity ratios in copolymerization. J. Macromol. Sci. Part A Chem. 1950, 5, 259–262. [Google Scholar] [CrossRef]
- Kelen, T.; Tüdos, F. Analysis of the Linear Methods for Determining Copolymerization Reactivity Ratios. I. A New Improved Linear Graphic Method. J. Macromol. Sci. Part A Chem. 1975, 9, 1–27. [Google Scholar] [CrossRef]
- Beginn, U. COPOINT—A simple computer program to determine copolymerization parameters by numerical integration. E-Polymers 2005, 5, 759–773. [Google Scholar] [CrossRef]
- Touchal, S.; Jonquières, A.; Clément, R.; Lochon, P. Copolymerization of 1-vinylpyrrolidone with N-substituted methacrylamides: Monomer reactivity ratios and copolymer sequence distribution. Polymer 2004, 45, 8311–8322. [Google Scholar] [CrossRef]
- Vijay Kumar, S.; Musturappa, T.E.; Prasannakumar, S.; Mahadevan, K.M.; Sherigara, B.S. N-Vinylpyrrolidone and Ethoxyethyl Methacrylate Copolymer: Synthesis, Characterization and Reactivity Ratios. J. Macromol. Sci. A 2007, 44, 1161–1169. [Google Scholar] [CrossRef]
- Vijay Kumar, S.; Prasannakumar, S.; Sherigara, B.S.; Redddy, B.S.R.; Aminabhavi, T.M. N-vinylpyrrolidone and 4-vinyl Benzylchloride Copolymers: Synthesis, Characterization and Reactivity Ratios. J. Macromol. Sci. A 2008, 45, 821–827. [Google Scholar] [CrossRef]
- Tripathi, A.; Srivastava, A.K. Studies on the radical polymerization of N-vinyl 2-pyrrolidone initiated by diphenyl ditelluride. J. Polym. Res. 2008, 15, 187–193. [Google Scholar] [CrossRef]
- Igarashi, S. Representation of composition and blockiness of the copolymer by a triangular coordinate system. J. Polym. Sci. Part B Polym. Lett. 1963, 1, 359–363. [Google Scholar] [CrossRef]
- Elias, H.G. Macromolecules. Synthesis, Materials, and Technology; Springer: New York, NY, USA, 1984; Volume 2. [Google Scholar]
- Devasia, R.; Nair, C.R.; Ninan, K.N. Polyacrylonitrile precursors for carbon fiber with imidocarbox ylic acid units: Copolymerization of acrylonitrile with maleimidobenzoic acid. J. Macromol. Sci. A 2002, 39, 693–708. [Google Scholar] [CrossRef]
- Barson, C.A.; Fenn, D.R. A method for determining reactivity ratios when copolymerizations are influenced by penultimate group effects. Eur. Polym. J. 1987, 23, 833–834. [Google Scholar] [CrossRef]
- Huma, F.; Akhter, Z.; Zafar-Uz-Zaman, M.; Yasin, T. Release of dexamethasone from poly(N-vinyl pyrrolidone-co-n-hexyl methacrylate) copolymers of controlled hydrophilicity. J. Appl. Polym. Sci. 2013, 128, 444–450. [Google Scholar] [CrossRef]
- Mitsoni, E.; Roka, N.; Pitsikalis, M. Statistical copolymerization of N-vinyl-pyrrolidone and alkyl methacrylates via RAFT: Reactivity ratios and thermal properties. J. Polym. Res. 2019, 26, 118. [Google Scholar] [CrossRef]
- Roka, N.; Kokkorogianni, O.; Pitsikalis, M. Statistical copolymers of N-vinylpyrrolidone and 2-(dimethylamino)ethyl methacrylate via RAFT: Monomer reactivity ratios, thermal properties, and kinetics of thermal decomposition. J. Polym. Sci. Part A Polym. Chem. 2017, 55, 3776–3787. [Google Scholar] [CrossRef]
- Roka, N.; Pitsikalis, M. Statistical copolymers of N-vinylpyrrolidone and benzyl methacrylate via RAFT: Monomer reactivity ratios, thermal properties and kinetics of thermal decomposition. J. Macromol. Sci. A 2018, 55, 222–230. [Google Scholar] [CrossRef]
- Gikarakis, T.; Pappas, I.; Arvanitaki, P.; Pantazi, E.; Mitsoni, E.; Roka, N.; Pitsikalis, M. Thermal Stability and Kinetics of Thermal Decomposition of Statistical Copolymers of N-vinyl-pyrrolidone and Alkyl Methacrylates Synthesized via RAFT Polymerization. J. Chem. 2021. accepted for publication. [Google Scholar]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef] [Green Version]
- Flynn, J.H.; Wall, L.A. A quick, direct method for the determination of activation energy from thermogravimetric data. J. Polym. Sci. Polym. Lett. Ed. 1966, 4, 323–328. [Google Scholar] [CrossRef]
- Ozawa, T. Kinetic analysis of derivative curves in thermal analysis. J. Therm. Anal. 1970, 2, 301–324. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction Kinetics in Differential Thermal Analysis. Anal. Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Kissinger, H.E. Variation of peak temperature with heating rate in differential thermal analysis. J. Res. Nat. Bur. Stand. 1956, 57, 217–221. [Google Scholar] [CrossRef]
- Galukhin, A.; Liavitskaya, T.; Vyazovkin, S. Kinetic and mechanistic insights into thermally initiated polymerization of cyanate esters with different bridging groups. Macromol. Chem. Phys. 2019, 220, 1900141. [Google Scholar] [CrossRef]
- Boulkadid, M.K.; Touidjine, S.; Trache, D.; Belkhiri, S. Analytical methods for the assessment of curing kinetics of polyurethane binders for high energy composites. Crit. Rev. Anal. Chem. 2020, 1–10. [Google Scholar] [CrossRef]
- Tarchoun, A.F.; Trache, D.; Klapötke, T.M.; Chelouche, S.; Derradji, M.; Bessa, W.; Mezroua, A. A promising energetic polymer from Posidonia oceanica brown alge: Synthesis, characterization, and kinetic modeling. Macromol. Chem. Phys. 2019, 220, 1900358. [Google Scholar] [CrossRef]
- Liqing, L.; Donghua, C. Application of iso-temperature method of multiple rate to kinetic analysis. Dehydration for calcium oxalate monohydrate J. Therm. Anal. Calorim. 2004, 78, 283–293. [Google Scholar] [CrossRef]
- Lim, A.C.R.; Chin, B.L.F.; Jawad, Z.A.; Hii, K.L. Kinetic analysis of rice husk pyrolysis using Kissinger-Akahira-Sunose (KAS) method. Proc. Engin. 2016, 148, 1247–1251. [Google Scholar] [CrossRef] [Green Version]
- Hayoune, F.; Chelouche, S.; Trache, D.; Zitouni, S.; Grohens, Y. Thermal decomposition kinetics and lifetime prediction of a PP/PLA blend supplemented with iron stearate during artificial aging. Thermochimica Acta 2020, 690, 178700. [Google Scholar] [CrossRef]
- Trache, D.; Abdelaziz, A.; Siouani, B. A simple and linear isoconversional method to determine the pre-exponential factors and the mathematical reaction mechanism functions. J. Therm. Anal. Calorim. 2017, 128, 335–348. [Google Scholar] [CrossRef]
- Doyle, C.D. Kinetic analysis of thermogravimetric data. J. Appl. Polym. Sci. 1961, 5, 285–292. [Google Scholar] [CrossRef]











| Sample | Mw × 10−3 (Daltons) a | Đ a | Conversion % | % mol NVP b | % mol IBMA b |
|---|---|---|---|---|---|
| F20-80 | 628 | 1.98 | 28 | 10 | 90 |
| F40-60 | 537 | 2.18 | 29 | 22 | 78 |
| F50-50 | 785 | 2.09 | 13 | 31 | 69 |
| F60-40 | 587 | 2.25 | 26 | 39 | 61 |
| F80-20 | 961 | 2.10 | 18 | 61 | 39 |
| R20-80 | 330 | 1.65 | 19 | 6 | 94 |
| R40-60 | 160 | 1.66 | 34 | 12 | 88 |
| R50-50 | 250 | 1.68 | 21 | 13 | 87 |
| R60-40 | 160 | 1.70 | 21 | 24 | 76 |
| R80-20 | 130 | 1.72 | 23 | 31 | 69 |
| Sample | M(NVP) | dM(NVP) | M(IBMA) | dM(IBMA) | X | Y | Gm | Hm | Gm/Hm | 1/Hm | η | ξ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F20/80 | 0.2194 | 0.1000 | 0.7806 | 0.9000 | 0.2811 | 0.1111 | −2.2485 | 0.7110 | −3.1626 | 1.4065 | −0.6255 | 0.1978 |
| F40/60 | 0.4175 | 0.2158 | 0.5825 | 0.7842 | 0.7167 | 0.2752 | −1.8878 | 1.8668 | −1.0113 | 0.5357 | −0.3974 | 0.3929 |
| F50/50 | 0.5110 | 0.3118 | 0.4890 | 0.6882 | 1.0450 | 0.4531 | −1.2615 | 2.4103 | −0.5234 | 0.4149 | −0.2383 | 0.4553 |
| F60/40 | 0.6127 | 0.3900 | 0.3873 | 0.6100 | 1.5820 | 0.6393 | −0.8924 | 3.9144 | −0.2280 | 0.2555 | −0.1313 | 0.5758 |
| F80/20 | 0.8089 | 0.6050 | 0.1911 | 0.3950 | 4.2329 | 1.5316 | 1.4693 | 11.6980 | 0.1256 | 0.0855 | 0.1008 | 0.8022 |
| Method | rNVP | rIBMA |
|---|---|---|
| Fineman-Ross | 0.329 | 2.321 |
| Inv. Fineman-Ross | 0.404 | 2.528 |
| Kelen-Tüdos | 0.365 | 2.438 |
| Ext. Kelen-Tüdos | 0.282 | 2.736 |
| COPOINT | 0.292 | 2.673 |
| Sample | M(NVP)-M(NVP) | M(IBMA)-M(IBMA) | M(NVP)-M(IBMA) | μ(NVP) | μ(IBMA) |
|---|---|---|---|---|---|
| F20/80 | 0.0082 | 0.8082 | 0.1837 | 1.08 | 10.51 |
| F40/60 | 0.0398 | 0.6082 | 0.3521 | 1.21 | 4.73 |
| F50/50 | 0.0860 | 0.4624 | 0.4515 | 1.30 | 3.56 |
| F60/40 | 0.1382 | 0.3582 | 0.5036 | 1.46 | 2.69 |
| F80/20 | 0.3520 | 0.1420 | 0.5060 | 2.24 | 1.63 |
| Reactivity Ratio | COPOINT | Barson-Fenn |
|---|---|---|
| r1 | 2.769 < 4.466 < 7.145 | 4.009 |
| r2 | 0.000 < 0.000 < 0.000 | Assumed 0 |
| r′1 | 14.533 < 14.830 < 15.126 | 6.510 |
| r′2 | 0.000 < 0.000 < 0.000 | Assumed 0 |
| Sample | Tg, °C |
|---|---|
| PNVP | 187 |
| PIBMA | 205 |
| R20-80 | 204.4 |
| R40-60 | 194.4 |
| R50-50 | 193.3 |
| R60-40 | 192.1 |
| R80-20 | 189.3 |
| Sample | Ea1 | Ea2 | Ea3 |
|---|---|---|---|
| PIBMA | 257.9 | 173.26 | 140.76 |
| R20-80 | 262.72 | 147.41 | 138.26 |
| R40-60 | 277.77 | 172.27 | 144.33 |
| R50-50 | 191.14 | 129.28 | 120.47 |
| R60-40 | 139.43 | 130.45 | 191.64 |
| R80-20 | 117.89 | 133.52 | 193.54 |
| PVP | 199.03 | - | - |
| Conversion | PIBMA | R20-80 | R40-60 | R50-50 | R60-40 | R80-20 | NVP |
|---|---|---|---|---|---|---|---|
| a = 0.1 | 265.88 | 309.86 | 189.64 | 143.42 | 159.05 | 158.88 | 58.20 |
| a = 0.2 | 249.34 | 190.14 | 191.72 | 142.42 | 145.83 | 147.24 | 173.35 |
| a = 0.3 | 232.13 | 181.58 | 187.15 | 138.43 | 140.76 | 143.67 | 191.80 |
| a = 0.4 | 211.09 | 166.20 | 178.67 | 137.10 | 135.52 | 141.84 | 197.12 |
| a = 0.5 | 179.75 | 162.12 | 176.01 | 133.86 | 130.70 | 138.84 | 199.54 |
| a = 0.6 | 149.74 | 161.54 | 169.36 | 132.44 | 126.71 | 137.18 | 201.61 |
| a = 0.7 | 127.37 | 192.80 | 165.61 | 142.25 | 192.64 | 198.71 | 203.19 |
| a = 0.8 | 117.31 | 179.75 | 218.33 | 210.09 | 236.20 | 227.55 | 204.86 |
| a = 0.9 | 153.23 | 258.23 | - | - | - | - | 203.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kokkorogianni, O.; Kontoes-Georgoudakis, P.; Athanasopoulou, M.; Polizos, N.; Pitsikalis, M. Statistical Copolymers of N-Vinylpyrrolidone and Isobornyl Methacrylate via Free Radical and RAFT Polymerization: Monomer Reactivity Ratios, Thermal Properties, and Kinetics of Thermal Decomposition. Polymers 2021, 13, 778. https://doi.org/10.3390/polym13050778
Kokkorogianni O, Kontoes-Georgoudakis P, Athanasopoulou M, Polizos N, Pitsikalis M. Statistical Copolymers of N-Vinylpyrrolidone and Isobornyl Methacrylate via Free Radical and RAFT Polymerization: Monomer Reactivity Ratios, Thermal Properties, and Kinetics of Thermal Decomposition. Polymers. 2021; 13(5):778. https://doi.org/10.3390/polym13050778
Chicago/Turabian StyleKokkorogianni, Olga, Philippos Kontoes-Georgoudakis, Maria Athanasopoulou, Nikolaos Polizos, and Marinos Pitsikalis. 2021. "Statistical Copolymers of N-Vinylpyrrolidone and Isobornyl Methacrylate via Free Radical and RAFT Polymerization: Monomer Reactivity Ratios, Thermal Properties, and Kinetics of Thermal Decomposition" Polymers 13, no. 5: 778. https://doi.org/10.3390/polym13050778
APA StyleKokkorogianni, O., Kontoes-Georgoudakis, P., Athanasopoulou, M., Polizos, N., & Pitsikalis, M. (2021). Statistical Copolymers of N-Vinylpyrrolidone and Isobornyl Methacrylate via Free Radical and RAFT Polymerization: Monomer Reactivity Ratios, Thermal Properties, and Kinetics of Thermal Decomposition. Polymers, 13(5), 778. https://doi.org/10.3390/polym13050778