Layer Adhesion Test of Additively Manufactured Pins: A Shear Test
Abstract
:1. Introduction
2. Materials and Methods
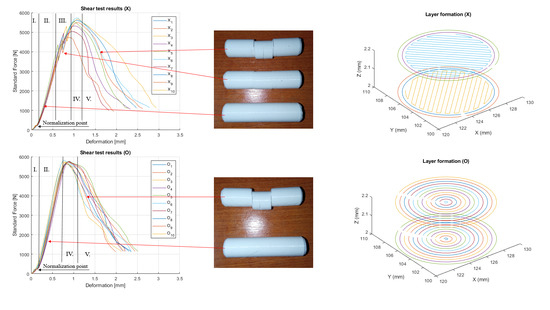
3. Results and Discussion
3.1. Explanation for the Test Results
3.2. Difference between the Layer Filling Methods
4. Effect of the Contour Lines and Stress Distribution
- How do the two contour lines affect the X samples?
- Do the contour lines affect the maximum shear stress?
5. Conclusions
- -
- The failure mechanism for the O specimens is well defined, and it follows a bilinear characteristic. However, the X specimens have a random initial failure mode, where some adhesive bonds break but the cross-section is still capable of holding more applied load.
- -
- The predicted behavior can be ensured by adding more uninterrupted contact regions such as the tested concentric cylindrical infill structure.
- -
- The obtained result is that for O-type layer formation, the shear stress would be around 46.1 MPa, and this value can later be used for failure prediction and numerical simulation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wong, K.V.; Hernandez, A. A Review of Additive Manufacturing. Int. Sch. Res. Netw. 2012, 2012, 208760. [Google Scholar] [CrossRef] [Green Version]
- Haghbin, N.; Bone, D.; Young, K. Controlled extrusion-based 3D printing of micro-channels with the geometric modelling of deposited roads. J. Manuf. Process. 2021, 67, 406–417. [Google Scholar] [CrossRef]
- Xiao, J.; Ji, G.; Zhang, Y.; Ma, G.; Mechtcherine, V.; Pan, J.; Wang, L.; Ding, T.; Duan, Z.; Du, S. Large-scale 3D printing concrete technology: Current status and future opportunities. Cem. Concr. Compos. 2021, 122, 104115. [Google Scholar] [CrossRef]
- Huang, S.H.; Liu, P.; Mokasdar, A.; Hou, L. Additive manufacturing and its societal impact: A literature review. Int. J. Adv. Manuf. Technol. 2013, 67, 1191–1203. [Google Scholar] [CrossRef]
- Yang, S.; Zhao, Y.F. Additive manufacturing-enabled design theory and methodology: A critical review. Int. J. Adv. Manuf. Technol. 2015, 80, 327–342. [Google Scholar] [CrossRef]
- Zhang, J.; Yanagimoto, J. Density-based topology optimization integrated with genetic algorithm for optimizing formability and bending stiffness of 3D printed CFRP core sandwich sheets. Compos. Part B Eng. 2021, 225, 109248. [Google Scholar] [CrossRef]
- Cheng, L.; Liu, J.; Liang, X.; To, A.C. Coupling lattice structure topology optimization with design-dependent feature evolution for additive manufactured heat conduction design. Comput. Methods Appl. Mech. Eng. 2018, 332, 408–439. [Google Scholar] [CrossRef]
- Liu, L.; Yi, B.; Wang, T.; Li, Z.; Zhang, J.; Yoon, G.H. Investigation on numerical analysis and mechanics experiments for topology optimization of functionally graded lattice structure. Addit. Manuf. 2021, 47, 102275. [Google Scholar] [CrossRef]
- Wang, H.; Du, W.; Zhao, Y.; Wang, Y.; Hao, R.; Yang, M. Joints for treelike column structures based on generative design and additive manufacturing. J. Constr. Steel Res. 2021, 184, 106794. [Google Scholar] [CrossRef]
- Allum, J.; Moetazedian, A.; Gleadall, A.; Silberschmidt, V.V. Interlayer bonding has bulk-material strength in extrusion additive manufacturing: New understanding of anisotropy. Addit. Manuf. 2020, 34, 101297. [Google Scholar] [CrossRef]
- Hmeidat, N.S.; Pack, R.C.; Talley, S.J.; Moore, R.B.; Compton, B.G. Mechanical anisotropy in polymer composites produced by material extrusion additive manufacturing. Addit. Manuf. 2020, 34, 101385. [Google Scholar] [CrossRef]
- Zharylkassyn, B.; Perveen, A.; Talamona, D. Effect of process parameters and materials on the dimensional accuracy of FDM parts. Mater. Today Proc. 2021, 44, 1307–1311. [Google Scholar] [CrossRef]
- Mohanty, A.; Nag, K.S.; Bagal, D.K.; Barua, A.; Jeet, S.; Mahapatra, S.S.; Cherkia, H. Parametric optimization of parameters affecting dimension precision of FDM printed part using hybrid Taguchi-MARCOS-nature inspired heuristic optimization technique. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Pennington, R.C.; Hoekstra, N.L.; Newcomer, J.L. Significant factors in the dimensional accuracy of fused deposition modelling. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2005, 219, 89–92. [Google Scholar] [CrossRef]
- Buj-Corral, I.; Bagheri, A.; Sivatte-Adroer, M. Effect of Printing Parameters on Dimensional Error, Surface Roughness and Porosity of FFF Printed Parts with Grid Structure. Polymers 2021, 13, 1213. [Google Scholar] [CrossRef]
- Torres, J.; Cotelo, J.; Karl, J.; Gordon, A.P. Mechanical Property Optimization of FDM PLA in Shear with Multiple Objectives. JOM 2015, 67, 1183–1193. [Google Scholar] [CrossRef]
- Dev, S.; Srivastava, R. Optimization of fused deposition modeling (FDM) process parameters for flexural strength. Mater. Today Proc. 2021, 44, 3012–3016. [Google Scholar] [CrossRef]
- Priyanka, G.; Kumar, K.; Reddy, V.G.P.; Tadepalli, T. Mechanical reliability of extruded PLA filaments. Materialia 2021, 16, 101075. [Google Scholar] [CrossRef]
- Bardiya, S.; Jerald, J.; Satheeshkumar, V. Effect of process parameters on the impact strength of fused filament fabricated (FFF) polylactic acid (PLA) parts. Mater. Today Proc. 2021, 41, 1103–1106. [Google Scholar] [CrossRef]
- Andó, M.; Birosz, M.; Jeganmohan, S. Surface bonding of additive manufactured parts from multi-colored PLA materials. Measurement 2021, 169, 108583. [Google Scholar] [CrossRef]
- MIL-STD-1312-13, Fastener Test Methods: Method 13, Double Shear Test 1984. Available online: http://everyspec.com/MIL-STD/MIL-STD-1300-1399/MIL_STD_1312_13_661/ (accessed on 1 November 2021).
- Osswald, T.A.; Menges, G. Material Science of Polymers for Engineers, 3rd ed.; Carl Hanser Verlag GmbH & Co. KG: München, Germany, 2012; ISBN 978-1-56990-514-2. [Google Scholar]
- Ugural, A.C.; Fenster, S.K. Advanced Mechanics of Materials and Applied Elasticity, 6th ed.; Pearson: Boston, MA, USA, 2020. [Google Scholar]
- Cantrell, J.T.; Rohde, S.; Damiani, D.; Gurnani, R.; DiSandro, L.; Anton, J.; Young, A.; Jerez, A.; Steinbach, D.; Kroese, C.; et al. Experimental characterization of the mechanical properties of 3D-printed ABS and polycarbonate parts. Rapid Prototyp. J. 2017, 23, 811–824. [Google Scholar] [CrossRef]
- Kuncius, T.; Rimašauskas, M.; Rimašauskienė, R. Interlayer Adhesion Analysis of 3D-Printed Continuous Carbon Fibre-Reinforced Composites. Polymers 2021, 13, 1653. [Google Scholar] [CrossRef]











| Material | PLA |
|---|---|
| Filament diameter [mm] | 1.75 |
| Printing temperature [°C] | 190–220 |
| Bed temperature [°C] | 50–60 |
| Density [g/cm3] | 1.24 |
| Color | White |
| Tensile strength [MPa] | ~47 |
| Tensile modulus [MPa] | 2100 |
| Force (N) | Shear Stress (MPa) | ||
|---|---|---|---|
| Mean | Std. Dev. | ||
| O12 | 2862 | 49.9 | 47.6 |
| O9 | 1939 | 39.9 | 43.4 |
| O6 | 1496 | 29.4 | 47.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Birosz, M.T.; Andó, M.; Safranyik, F. Layer Adhesion Test of Additively Manufactured Pins: A Shear Test. Polymers 2022, 14, 55. https://doi.org/10.3390/polym14010055
Birosz MT, Andó M, Safranyik F. Layer Adhesion Test of Additively Manufactured Pins: A Shear Test. Polymers. 2022; 14(1):55. https://doi.org/10.3390/polym14010055
Chicago/Turabian StyleBirosz, Márton Tamás, Mátyás Andó, and Ferenc Safranyik. 2022. "Layer Adhesion Test of Additively Manufactured Pins: A Shear Test" Polymers 14, no. 1: 55. https://doi.org/10.3390/polym14010055
APA StyleBirosz, M. T., Andó, M., & Safranyik, F. (2022). Layer Adhesion Test of Additively Manufactured Pins: A Shear Test. Polymers, 14(1), 55. https://doi.org/10.3390/polym14010055