Sensors and Sensor Fusion Methodologies for Indoor Odometry: A Review
Abstract
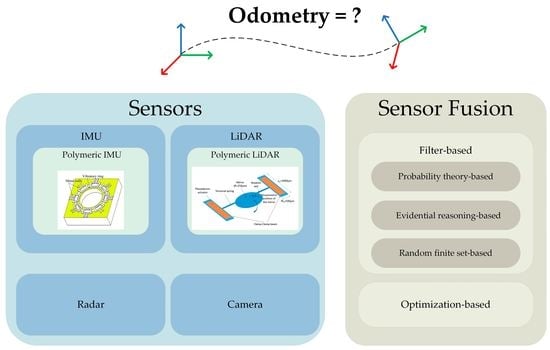
:1. Introduction
2. Sensors and Sensor-Based Odometry Methods
2.1. Wheel Odometer
2.2. Inertial Measurement Units (IMUs)

2.3. LiDAR
| Category | Method | Loop-Closure Detection | Accuracy 1 | Runtime 1 |
|---|---|---|---|---|
| Scan-matching | ICP [70] | No | Medium | High |
| NDT [76] | No | Medium | High | |
| GMM [77] | No | Medium | - | |
| IMLS [82] | No | High | High | |
| MULLS [86] | Yes | High | Medium | |
| Surfel-based [83] | Yes | Medium | Medium | |
| DLO [101] | No | High | Low | |
| ELO [102] | No | High | Low | |
| Feature-based | Feature descriptor [97] | No | Low | High |
| LOAM [98] | No | High | Medium | |
| LeGO-LOAM [99] | No | High | Low | |
| SA-LOAM [103] | Yes | High | Medium |
2.4. Millimeter Wave (MMW) Radar
2.5. Vision
2.6. Discussion
3. Sensor Fusion
3.1. Filter-Based
3.1.1. Probability-Theory-Based
3.1.2. Evidential-Reasoning-Based
3.1.3. Random-Finite-Set-Based
3.2. Optimization-Based
3.3. Discussion
4. Future Prospects
4.1. Embedded Sensors for Soft Robots’ State Estimation and Perception
4.2. Swarm Odometry
4.3. Accelerating Processing Speed at the Hardware Level
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- El-Sheimy, N.; Li, Y. Indoor navigation: State of the art and future trends. Satell. Navig. 2021, 2, 7. [Google Scholar] [CrossRef]
- Everett, H. Sensors for Mobile Robots; AK Peters/CRC Press: New York, NY, USA, 1995. [Google Scholar]
- Civera, J.; Lee, S.H. RGB-D Odometry and SLAM. In RGB-D Image Analysis and Processing; Rosin, P.L., Lai, Y.-K., Shao, L., Liu, Y., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 117–144. [Google Scholar]
- Ashley, P.; Temmen, M.; Diffey, W.; Sanghadasa, M.; Bramson, M.; Lindsay, G.; Guenthner, A. Components for IFOG Based Inertial Measurement Units Using Active and Passive Polymer Materials; SPIE: Sandiego, CA, USA, 2006; Volume 6314. [Google Scholar]
- Hellebrekers, T.; Ozutemiz, K.B.; Yin, J.; Majidi, C. Liquid Metal-Microelectronics Integration for a Sensorized Soft Robot Skin. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 5924–5929. [Google Scholar]
- Bresson, G.; Alsayed, Z.; Yu, L.; Glaser, S. Simultaneous Localization and Mapping: A Survey of Current Trends in Autonomous Driving. IEEE Trans. Intell. Veh. 2017, 2, 194–220. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, S.A.S.; Haghbayan, M.H.; Westerlund, T.; Heikkonen, J.; Tenhunen, H.; PLoSila, J. A Survey on Odometry for Autonomous Navigation Systems. IEEE Access 2019, 7, 97466–97486. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, J.; Liu, J. A survey of simultaneous localization and mapping with an envision in 6g wireless networks. arXiv 2019, arXiv:1909.05214. [Google Scholar]
- Chen, C.; Wang, B.; Lu, C.X.; Trigoni, N.; Markham, A. A survey on deep learning for localization and mapping: Towards the age of spatial machine intelligence. arXiv 2020, arXiv:2006.12567. [Google Scholar]
- Fayyad, J.; Jaradat, M.A.; Gruyer, D.; Najjaran, H. Deep Learning Sensor Fusion for Autonomous Vehicle Perception and Localization: A Review. Sensors 2020, 20, 4220. [Google Scholar] [CrossRef]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef]
- Taheri, H.; Xia, Z.C. SLAM; definition and evolution. Eng. Appl. Artif. Intell. 2021, 97, 104032. [Google Scholar] [CrossRef]
- Servières, M.; Renaudin, V.; Dupuis, A.; Antigny, N. Visual and Visual-Inertial SLAM: State of the Art, Classification, and Experimental Benchmarking. J. Sens. 2021, 2021, 2054828. [Google Scholar] [CrossRef]
- Tzafestas, S.G. 4—Mobile Robot Sensors. In Introduction to Mobile Robot Control; Tzafestas, S.G., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 101–135. [Google Scholar]
- Thomas, S.; Froehly, A.; Bredendiek, C.; Herschel, R.; Pohl, N. High Resolution SAR Imaging Using a 240 GHz FMCW Radar System with Integrated On-Chip Antennas. In Proceedings of the 15th European Conference on Antennas and Propagation (EuCAP), Virtual, 22–26 March 2021; pp. 1–5. [Google Scholar]
- Brossard, M.; Bonnabel, S. Learning Wheel Odometry and IMU Errors for Localization. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 291–297. [Google Scholar]
- Woodman, O.J. An Introduction to Inertial Navigation; University of Cambridge: Cambridge, UK, 2007. [Google Scholar]
- Siciliano, B.; Khatib, O. Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D. Introduction to Autonomous Mobile Robots; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Ahmed, A.; Pandit, S.; Patkar, R.; Dixit, P.; Baghini, M.S.; Khlifi, A.; Tounsi, F.; Mezghani, B. Induced-Stress Analysis of SU-8 Polymer Based Single Mass 3-Axis Piezoresistive MEMS Accelerometer. In Proceedings of the 16th International Multi-Conference on Systems, Signals & Devices (SSD), Istanbul, Turkey, 21–24 March 2019; pp. 131–136. [Google Scholar]
- Wan, F.; Qian, G.; Li, R.; Tang, J.; Zhang, T. High sensitivity optical waveguide accelerometer based on Fano resonance. Appl. Opt. 2016, 55, 6644–6648. [Google Scholar] [CrossRef]
- Yi, J. A Piezo-Sensor-Based “Smart Tire” System for Mobile Robots and Vehicles. IEEE/ASME Trans. Mechatron. 2008, 13, 95–103. [Google Scholar] [CrossRef]
- Passaro, V.M.N.; Cuccovillo, A.; Vaiani, L.; De Carlo, M.; Campanella, C.E. Gyroscope Technology and Applications: A Review in the Industrial Perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El-Sheimy, N.; Youssef, A. Inertial sensors technologies for navigation applications: State of the art and future trends. Satell. Navig. 2020, 1, 2. [Google Scholar] [CrossRef] [Green Version]
- Hakyoung, C.; Ojeda, L.; Borenstein, J. Accurate mobile robot dead-reckoning with a precision-calibrated fiber-optic gyroscope. IEEE Trans. Robot. Autom. 2001, 17, 80–84. [Google Scholar] [CrossRef]
- Qian, G.; Tang, J.; Zhang, X.-Y.; Li, R.-Z.; Lu, Y.; Zhang, T. Low-Loss Polymer-Based Ring Resonator for Resonant Integrated Optical Gyroscopes. J. Nanomater. 2014, 2014, 146510. [Google Scholar] [CrossRef]
- Yeh, C.N.; Tsai, J.J.; Shieh, R.J.; Tseng, F.G.; Li, C.J.; Su, Y.C. A vertically supported ring-type mems gyroscope utilizing electromagnetic actuation and sensing. In Proceedings of the IEEE International Conference on Electron Devices and Solid-State Circuits, Hong Kong, China, 8–10 December 2008; pp. 1–4. [Google Scholar]
- Ward, C.C.; Iagnemma, K. A Dynamic-Model-Based Wheel Slip Detector for Mobile Robots on Outdoor Terrain. IEEE Trans. Robot. 2008, 24, 821–831. [Google Scholar] [CrossRef]
- Yi, J.; Wang, H.; Zhang, J.; Song, D.; Jayasuriya, S.; Liu, J. Kinematic Modeling and Analysis of Skid-Steered Mobile Robots With Applications to Low-Cost Inertial-Measurement-Unit-Based Motion Estimation. IEEE Trans. Robot. 2009, 25, 1087–1097. [Google Scholar] [CrossRef] [Green Version]
- Bancroft, J.B. Multiple IMU integration for vehicular navigation. In Proceedings of the Proceedings of the 22nd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 1828–1840. [Google Scholar]
- Wu, Y.; Niu, X.; Kuang, J. A Comparison of Three Measurement Models for the Wheel-mounted MEMS IMU-based Dead Reckoning System. arXiv 2020, arXiv:2012.10589. [Google Scholar] [CrossRef]
- Lupton, T.; Sukkarieh, S. Visual-Inertial-Aided Navigation for High-Dynamic Motion in Built Environments Without Initial Conditions. IEEE Trans. Robot. 2012, 28, 61–76. [Google Scholar] [CrossRef]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual—Inertial Odometry. IEEE Trans. Robot. 2017, 33, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Brossard, M.; Barrau, A.; Chauchat, P.; Bonnabel, S. Associating Uncertainty to Extended Poses for on Lie Group IMU Preintegration With Rotating Earth. IEEE Trans. Robot. 2021, 3, 998–1015. [Google Scholar] [CrossRef]
- Quick Start for MTi Development Kit. Available online: https://xsenstechnologies.force.com/knowledgebase/s/article/Quick-start-for-MTi-Development-Kit-1605870241724?language=en_US (accessed on 1 March 2022).
- ROS (Robot Operating System) Drivers | MicroStrain. Available online: https://www.microstrain.com/software/ros (accessed on 1 March 2022).
- Mukherjee, A. Visualising 3D Motion of IMU Sensor. Available online: https://create.arduino.cc/projecthub/Aritro/visualising-3d-motion-of-imu-sensor-3933b0?f=1 (accessed on 1 March 2022).
- Borodacz, K.; Szczepański, C.; Popowski, S. Review and selection of commercially available IMU for a short time inertial navigation. Aircr. Eng. Aerosp. Technol. 2022, 94, 45–59. [Google Scholar] [CrossRef]
- Behroozpour, B.; Sandborn, P.A.M.; Wu, M.C.; Boser, B.E. Lidar System Architectures and Circuits. IEEE Commun. Mag. 2017, 55, 135–142. [Google Scholar] [CrossRef]
- Khader, M.; Cherian, S. An Introduction to Automotive LIDAR, Texas Instruments; Technical Report; Taxes Instruments Incorporated: Dallas, TX, USA, 2018. [Google Scholar]
- Li, Y.; Ibanez-Guzman, J. Lidar for Autonomous Driving: The Principles, Challenges, and Trends for Automotive Lidar and Perception Systems. IEEE Signal Process Mag. 2020, 37, 50–61. [Google Scholar] [CrossRef]
- Royo, S.; Ballesta-Garcia, M. An Overview of Lidar Imaging Systems for Autonomous Vehicles. Appl. Sci. 2019, 9, 4093. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Watkins, C.; Xie, H. MEMS Mirrors for LiDAR: A Review. Micromachines 2020, 11, 456. [Google Scholar] [CrossRef]
- Yoo, H.W.; Druml, N.; Brunner, D.; Schwarzl, C.; Thurner, T.; Hennecke, M.; Schitter, G. MEMS-based lidar for autonomous driving. Elektrotechnik Inf. 2018, 135, 408–415. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Zhang, F. Loam livox: A fast, robust, high-precision LiDAR odometry and mapping package for LiDARs of small FoV. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 3126–3131. [Google Scholar]
- Amzajerdian, F.; Pierrottet, D.; Petway, L.B.; Hines, G.D.; Roback, V.E.; Reisse, R.A. Lidar sensors for autonomous landing and hazard avoidance. In Proceedings of the AIAA Space 2013 Conference and Exposition, San Diego, CA, USA, 10–12 September 2013; p. 5312. [Google Scholar]
- Dietrich, A.B.; McMahon, J.W. Robust Orbit Determination with Flash Lidar Around Small Bodies. J. Guid. Control. Dyn. 2018, 41, 2163–2184. [Google Scholar] [CrossRef]
- Poulton, C.V.; Byrd, M.J.; Russo, P.; Timurdogan, E.; Khandaker, M.; Vermeulen, D.; Watts, M.R. Long-Range LiDAR and Free-Space Data Communication With High-Performance Optical Phased Arrays. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–8. [Google Scholar] [CrossRef]
- Kim, S.-M.; Park, T.-H.; Im, C.-S.; Lee, S.-S.; Kim, T.; Oh, M.-C. Temporal response of polymer waveguide beam scanner with thermo-optic phase-modulator array. Opt. Express 2020, 28, 3768–3778. [Google Scholar] [CrossRef]
- Im, C.S.; Kim, S.M.; Lee, K.P.; Ju, S.H.; Hong, J.H.; Yoon, S.W.; Kim, T.; Lee, E.S.; Bhandari, B.; Zhou, C.; et al. Hybrid Integrated Silicon Nitride–Polymer Optical Phased Array For Efficient Light Detection and Ranging. J. Lightw. Technol. 2021, 39, 4402–4409. [Google Scholar] [CrossRef]
- Casset, F.; Poncet, P.; Desloges, B.; Santos, F.D.D.; Danel, J.S.; Fanget, S. Resonant Asymmetric Micro-Mirror Using Electro Active Polymer Actuators. In Proceedings of the IEEE SENSORS, New Delhi, India, 28–31 October 2018; pp. 1–4. [Google Scholar]
- Pavia, J.M.; Wolf, M.; Charbon, E. Measurement and modeling of microlenses fabricated on single-photon avalanche diode arrays for fill factor recovery. Opt. Express 2014, 22, 4202–4213. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Chen, S.; Liu, X.; Xu, H.; Wu, Y.; Li, M.; Chen, Y. Registration of Laser Scanning Point Clouds: A Review. Sensors 2018, 18, 1641. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saiti, E.; Theoharis, T. An application independent review of multimodal 3D registration methods. Comput. Graph. 2020, 91, 153–178. [Google Scholar] [CrossRef]
- Huang, X.; Mei, G.; Zhang, J.; Abbas, R. A comprehensive survey on point cloud registration. arXiv 2021, arXiv:2103.02690. [Google Scholar]
- Zhu, H.; Guo, B.; Zou, K.; Li, Y.; Yuen, K.-V.; Mihaylova, L.; Leung, H. A Review of Point Set Registration: From Pairwise Registration to Groupwise Registration. Sensors 2019, 19, 1191. [Google Scholar] [CrossRef] [Green Version]
- Holz, D.; Ichim, A.E.; Tombari, F.; Rusu, R.B.; Behnke, S. Registration with the Point Cloud Library: A Modular Framework for Aligning in 3-D. IEEE Robot. Autom. Mag. 2015, 22, 110–124. [Google Scholar] [CrossRef]
- Jonnavithula, N.; Lyu, Y.; Zhang, Z. LiDAR Odometry Methodologies for Autonomous Driving: A Survey. arXiv 2021, arXiv:2109.06120. [Google Scholar]
- Elhousni, M.; Huang, X. A Survey on 3D LiDAR Localization for Autonomous Vehicles. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1879–1884. [Google Scholar]
- Bosse, M.; Zlot, R. Keypoint design and evaluation for place recognition in 2D lidar maps. Rob. Auton. Syst. 2009, 57, 1211–1224. [Google Scholar] [CrossRef]
- Wang, D.Z.; Posner, I.; Newman, P. Model-free detection and tracking of dynamic objects with 2D lidar. Int. J. Robot. Res. 2015, 34, 1039–1063. [Google Scholar] [CrossRef]
- Zou, Q.; Sun, Q.; Chen, L.; Nie, B.; Li, Q. A Comparative Analysis of LiDAR SLAM-Based Indoor Navigation for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 1–15. [Google Scholar] [CrossRef]
- François, P.; Francis, C.; Roland, S. A Review of Point Cloud Registration Algorithms for Mobile Robotics. Found. Trends Robot. 2015, 4, 1–104. [Google Scholar]
- Münch, D.; Combès, B.; Prima, S. A Modified ICP Algorithm for Normal-Guided Surface Registration; SPIE: Bellingham, WA, USA, 2010; Volume 7623. [Google Scholar]
- Serafin, J.; Grisetti, G. NICP: Dense normal based point cloud registration. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 742–749. [Google Scholar]
- Godin, G.; Rioux, M.; Baribeau, R. Three-Dimensional Registration Using Range and Intensity Information; SPIE: Boston, MA, USA, 1994; Volume 2350. [Google Scholar]
- Greenspan, M.; Yurick, M. Approximate k-d tree search for efficient ICP. In Proceedings of the Fourth International Conference on 3-D Digital Imaging and Modeling, Banff, AB, Canada, 6–10 October 2003; pp. 442–448. [Google Scholar]
- Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A Globally Optimal Solution to 3D ICP Point-Set Registration. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2241–2254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, S.-Y.; Subbarao, M. An accurate and fast point-to-plane registration technique. Pattern Recognit. Lett. 2003, 24, 2967–2976. [Google Scholar] [CrossRef]
- Segal, A.; Haehnel, D.; Thrun, S. Generalized-icp. In Proceedings of the Robotics: Science and Systems, Seattle, WA, USA, 28 June–1 July 2009; p. 435. [Google Scholar]
- Yokozuka, M.; Koide, K.; Oishi, S.; Banno, A. LiTAMIN2: Ultra Light LiDAR-based SLAM using Geometric Approximation applied with KL-Divergence. arXiv 2021, arXiv:2103.00784. [Google Scholar]
- Lu, D.L. Vision-Enhanced Lidar Odometry and Mapping; Carnegie Mellon University: Pittsburgh, PA, USA, 2016. [Google Scholar]
- Biber, P.; Strasser, W. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the Proceedings IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Las Vegas, NV, USA, 27–31 October 2003; Volume 2743, pp. 2743–2748. [Google Scholar]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Rob. 2007, 24, 803–827. [Google Scholar] [CrossRef] [Green Version]
- Stoyanov, T.; Magnusson, M.; Andreasson, H.; Lilienthal, A.J. Fast and accurate scan registration through minimization of the distance between compact 3D NDT representations. Int. J. Robot. Res. 2012, 31, 1377–1393. [Google Scholar] [CrossRef]
- Magnusson, M.; Vaskevicius, N.; Stoyanov, T.; Pathak, K.; Birk, A. Beyond points: Evaluating recent 3D scan-matching algorithms. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 3631–3637. [Google Scholar]
- Wolcott, R.W.; Eustice, R.M. Robust LIDAR localization using multiresolution Gaussian mixture maps for autonomous driving. Int. J. Robot. Res. 2017, 36, 292–319. [Google Scholar] [CrossRef]
- Eckart, B.; Kim, K.; Kautz, J. Hgmr: Hierarchical gaussian mixtures for adaptive 3d registration. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 705–721. [Google Scholar]
- Myronenko, A.; Song, X. Point Set Registration: Coherent Point Drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [Green Version]
- Ji, K.; Chen, H.; Di, H.; Gong, J.; Xiong, G.; Qi, J.; Yi, T. CPFG-SLAM:a Robust Simultaneous Localization and Mapping based on LIDAR in Off-Road Environment. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; pp. 650–655. [Google Scholar]
- Fontanelli, D.; Ricciato, L.; Soatto, S. A Fast RANSAC-Based Registration Algorithm for Accurate Localization in Unknown Environments using LIDAR Measurements. In Proceedings of the IEEE International Conference on Automation Science and Engineering, Scottsdale, AZ, USA, 22–25 September 2007; pp. 597–602. [Google Scholar]
- Deschaud, J.-E. IMLS-SLAM: Scan-to-model matching based on 3D data. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–16 May 2018; pp. 2480–2485. [Google Scholar]
- Behley, J.; Stachniss, C. Efficient Surfel-Based SLAM using 3D Laser Range Data in Urban Environments. In Proceedings of the Robotics: Science and Systems, Pittsburgh, PA, USA, 26–30 June 2018. [Google Scholar]
- Quenzel, J.; Behnke, S. Real-time multi-adaptive-resolution-surfel 6D LiDAR odometry using continuous-time trajectory optimization. arXiv 2021, arXiv:2105.02010. [Google Scholar]
- Droeschel, D.; Schwarz, M.; Behnke, S. Continuous mapping and localization for autonomous navigation in rough terrain using a 3D laser scanner. Rob. Auton. Syst. 2017, 88, 104–115. [Google Scholar] [CrossRef]
- Pan, Y.; Xiao, P.; He, Y.; Shao, Z.; Li, Z. MULLS: Versatile LiDAR SLAM via Multi-metric Linear Least Square. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hybrid Event, 30 May–5 June 2021; pp. 11633–11640. [Google Scholar]
- Kim, H.; Hilton, A. Evaluation of 3D Feature Descriptors for Multi-modal Data Registration. In Proceedings of the International Conference on 3D Vision—3DV 2013, Seattle, WA, USA, 29 June–1 July 2013; pp. 119–126. [Google Scholar]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. 3D Object Recognition in Cluttered Scenes with Local Surface Features: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2270–2287. [Google Scholar] [CrossRef] [PubMed]
- Alexandre, L.A. 3D descriptors for object and category recognition: A comparative evaluation. In Proceedings of the Workshop on Color-Depth Camera Fusion in Robotics at the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura, Portugal, 7–12 October 2012; p. 7. [Google Scholar]
- He, Y.; Mei, Y. An efficient registration algorithm based on spin image for LiDAR 3D point cloud models. Neurocomputing 2015, 151, 354–363. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Tombari, F.; Salti, S.; Stefano, L.D. Unique shape context for 3d data description. In Proceedings of the ACM Workshop on 3D Object Retrieval, Firenze, Italy, 25 October 2010; pp. 57–62. [Google Scholar]
- Kim, G.; Kim, A. Scan Context: Egocentric Spatial Descriptor for Place Recognition Within 3D Point Cloud Map. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4802–4809. [Google Scholar]
- Tombari, F.; Salti, S.; Di Stefano, L. Unique Signatures of Histograms for Local Surface Description; Springer: Berlin/Heidelberg, Germany, 2010; pp. 356–369. [Google Scholar]
- Guo, J.; Borges, P.V.K.; Park, C.; Gawel, A. Local Descriptor for Robust Place Recognition Using LiDAR Intensity. IEEE Rob. Autom. Lett. 2019, 4, 1470–1477. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Wang, X.; Zhang, H. M2DP: A novel 3D point cloud descriptor and its application in loop closure detection. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 231–237. [Google Scholar]
- Skjellaug, E.; Brekke, E.F.; Stahl, A. Feature-Based Laser Odometry for Autonomous Surface Vehicles utilizing the Point Cloud Library. In Proceedings of the IEEE 23rd International Conference on Information Fusion (FUSION), Virtual, 6–9 July 2020; pp. 1–8. [Google Scholar]
- Zhang, J.; Singh, S. LOAM: Lidar Odometry and Mapping in Real-time. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014. [Google Scholar]
- Shan, T.; Englot, B. LeGO-LOAM: Lightweight and Ground-Optimized Lidar Odometry and Mapping on Variable Terrain. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- RoboStudio. Available online: https://www.slamtec.com/en/RoboStudio (accessed on 1 March 2022).
- Chen, K.; Lopez, B.T.; Agha-mohammadi, A.a.; Mehta, A. Direct LiDAR Odometry: Fast Localization With Dense Point Clouds. IEEE Rob. Autom. Lett. 2022, 7, 2000–2007. [Google Scholar] [CrossRef]
- Zheng, X.; Zhu, J. Efficient LiDAR Odometry for Autonomous Driving. IEEE Rob. Autom. Lett. 2021, 6, 8458–8465. [Google Scholar] [CrossRef]
- Li, L.; Kong, X.; Zhao, X.; Li, W.; Wen, F.; Zhang, H.; Liu, Y. SA-LOAM: Semantic-aided LiDAR SLAM with Loop Closure. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Virtual, 30 May–5 June 2021; pp. 7627–7634. [Google Scholar]
- Lu, W.; Wan, G.; Zhou, Y.; Fu, X.; Yuan, P.; Song, S. DeepVCP: An End-to-End Deep Neural Network for Point Cloud Registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019; pp. 12–21. [Google Scholar]
- Berlo, B.v.; Elkelany, A.; Ozcelebi, T.; Meratnia, N. Millimeter Wave Sensing: A Review of Application Pipelines and Building Blocks. IEEE Sens. J. 2021, 21, 10332–10368. [Google Scholar] [CrossRef]
- Waldschmidt, C.; Hasch, J.; Menzel, W. Automotive Radar—From First Efforts to Future Systems. IEEE J. Microw. 2021, 1, 135–148. [Google Scholar] [CrossRef]
- Jilani, S.F.; Munoz, M.O.; Abbasi, Q.H.; Alomainy, A. Millimeter-Wave Liquid Crystal Polymer Based Conformal Antenna Array for 5G Applications. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 84–88. [Google Scholar] [CrossRef] [Green Version]
- Geiger, M.; Waldschmidt, C. 160-GHz Radar Proximity Sensor With Distributed and Flexible Antennas for Collaborative Robots. IEEE Access 2019, 7, 14977–14984. [Google Scholar] [CrossRef]
- Hamouda, Z.; Wojkiewicz, J.-L.; Pud, A.A.; Kone, L.; Bergheul, S.; Lasri, T. Flexible UWB organic antenna for wearable technologies application. IET Microw. Antennas Propag. 2018, 12, 160–166. [Google Scholar] [CrossRef]
- Händel, C.; Konttaniemi, H.; Autioniemi, M. State-of-the-Art Review on Automotive Radars and Passive Radar Reflectors: Arctic Challenge Research Project; Lapland UAS: Rovaniemi, Finland, 2018. [Google Scholar]
- Patole, S.M.; Torlak, M.; Wang, D.; Ali, M. Automotive radars: A review of signal processing techniques. IEEE Signal Process Mag. 2017, 34, 22–35. [Google Scholar] [CrossRef]
- Ramasubramanian, K.; Ginsburg, B. AWR1243 Sensor: Highly Integrated 76–81-GHz Radar Front-End for Emerging ADAS Applications. Tex. Instrum. White Pap. 2017. Available online: https://www.ti.com/lit/wp/spyy003/spyy003.pdf?ts=1652435333581&ref_url=https%253A%252F%252Fwww.google.com%252F (accessed on 1 March 2022).
- Rao, S. Introduction to mmWave sensing: FMCW radars. In Texas Instruments (TI) mmWave Training Series; Texas Instruments: Dallas, TX, USA, 2017; Volume SPYY003, pp. 1–11. [Google Scholar]
- Hakobyan, G.; Yang, B. High-Performance Automotive Radar: A Review of Signal Processing Algorithms and Modulation Schemes. IEEE Signal Process Mag. 2019, 36, 32–44. [Google Scholar] [CrossRef]
- Meinl, F.; Schubert, E.; Kunert, M.; Blume, H. Real-Time Data Preprocessing for High-Resolution MIMO Radar Sensors. Comput. Sci. 2017, 133, 54916304. [Google Scholar]
- Gao, X.; Roy, S.; Xing, G. MIMO-SAR: A Hierarchical High-Resolution Imaging Algorithm for mmWave FMCW Radar in Autonomous Driving. IEEE Trans. Veh. Technol. 2021, 70, 7322–7334. [Google Scholar] [CrossRef]
- Rouveure, R.; Faure, P.; Monod, M.-O. PELICAN: Panoramic millimeter-wave radar for perception in mobile robotics applications, Part 1: Principles of FMCW radar and of 2D image construction. Rob. Auton. Syst. 2016, 81, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Rouveure, R.; Faure, P.; Monod, M.-O. Description and experimental results of a panoramic K-band radar dedicated to perception in mobile robotics applications. J. Field Rob. 2018, 35, 678–704. [Google Scholar] [CrossRef]
- Dickmann, J.; Klappstein, J.; Hahn, M.; Appenrodt, N.; Bloecher, H.; Werber, K.; Sailer, A. Automotive radar the key technology for autonomous driving: From detection and ranging to environmental understanding. In Proceedings of the IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Zhou, T.; Yang, M.; Jiang, K.; Wong, H.; Yang, D. MMW Radar-Based Technologies in Autonomous Driving: A Review. Sensors 2020, 20, 7283. [Google Scholar] [CrossRef]
- Cen, S. Ego-Motion Estimation and Localization with Millimeter-Wave Scanning Radar; University of Oxford: Oxford, UK, 2019. [Google Scholar]
- Vivet, D.; Gérossier, F.; Checchin, P.; Trassoudaine, L.; Chapuis, R. Mobile Ground-Based Radar Sensor for Localization and Mapping: An Evaluation of two Approaches. Int. J. Adv. Rob. Syst. 2013, 10, 307. [Google Scholar] [CrossRef]
- Checchin, P.; Gérossier, F.; Blanc, C.; Chapuis, R.; Trassoudaine, L. Radar Scan Matching SLAM Using the Fourier-Mellin Transform; Springer: Berlin/Heidelberg, Germany, 2010; pp. 151–161. [Google Scholar]
- Reddy, B.S.; Chatterji, B.N. An FFT-based technique for translation, rotation, and scale-invariant image registration. IEEE Trans. Image Process. 1996, 5, 1266–1271. [Google Scholar] [CrossRef] [Green Version]
- Park, Y.S.; Shin, Y.S.; Kim, A. PhaRaO: Direct Radar Odometry using Phase Correlation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Virtual, 31 May–31 August 2020; pp. 2617–2623. [Google Scholar]
- Kellner, D.; Barjenbruch, M.; Klappstein, J.; Dickmann, J.; Dietmayer, K. Instantaneous ego-motion estimation using multiple Doppler radars. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1592–1597. [Google Scholar]
- Holder, M.; Hellwig, S.; Winner, H. Real-Time Pose Graph SLAM based on Radar. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 1145–1151. [Google Scholar]
- Doer, C.; Trommer, G.F. An EKF Based Approach to Radar Inertial Odometry. In Proceedings of the IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Virtual Conference, 14–16 September 2020; pp. 152–159. [Google Scholar]
- Kramer, A.; Stahoviak, C.; Santamaria-Navarro, A.; Agha-mohammadi, A.a.; Heckman, C. Radar-Inertial Ego-Velocity Estimation for Visually Degraded Environments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Virtual Conference, 31 May–31 August 2020; pp. 5739–5746. [Google Scholar]
- Monaco, C.D.; Brennan, S.N. RADARODO: Ego-Motion Estimation From Doppler and Spatial Data in RADAR Images. IEEE Trans. Intell. Veh. 2020, 5, 475–484. [Google Scholar] [CrossRef]
- Dissanayake, M.W.M.G.; Newman, P.; Clark, S.; Durrant-Whyte, H.F.; Csorba, M. A solution to the simultaneous localization and map building (SLAM) problem. IEEE Trans. Robot. Autom. 2001, 17, 229–241. [Google Scholar] [CrossRef] [Green Version]
- Adams, M.; Adams, M.D.; Mullane, J.; Jose, E. Robotic Navigation and Mapping with Radar; Artech House: Boston, MA, USA, 2012. [Google Scholar]
- Mullane, J.; Jose, E.; Adams, M.D.; Wijesoma, W.S. Including probabilistic target detection attributes into map representations. Rob. Auton. Syst. 2007, 55, 72–85. [Google Scholar] [CrossRef]
- Adams, M.; Vo, B.; Mahler, R.; Mullane, J. SLAM Gets a PHD: New Concepts in Map Estimation. IEEE Robot. Autom. Mag. 2014, 21, 26–37. [Google Scholar] [CrossRef]
- Mullane, J.; Vo, B.; Adams, M.D.; Vo, B. A Random-Finite-Set Approach to Bayesian SLAM. IEEE Trans. Robot. 2011, 27, 268–282. [Google Scholar] [CrossRef]
- Schuster, F.; Keller, C.G.; Rapp, M.; Haueis, M.; Curio, C. Landmark based radar SLAM using graph optimization. In Proceedings of the IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 2559–2564. [Google Scholar]
- Hong, Z.; Petillot, Y.; Wang, S. RadarSLAM: Radar based Large-Scale SLAM in All Weathers. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2021; pp. 5164–5170. [Google Scholar]
- Callmer, J.; Törnqvist, D.; Gustafsson, F.; Svensson, H.; Carlbom, P. Radar SLAM using visual features. EURASIP J. Adv. Signal Process. 2011, 2011, 71. [Google Scholar] [CrossRef] [Green Version]
- Ward, E.; Folkesson, J. Vehicle localization with low cost radar sensors. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 864–870. [Google Scholar]
- Kung, P.-C.; Wang, C.-C.; Lin, W.-C. A Normal Distribution Transform-Based Radar Odometry Designed For Scanning and Automotive Radars. arXiv 2021, arXiv:2103.07908. [Google Scholar]
- Rapp, M.; Barjenbruch, M.; Hahn, M.; Dickmann, J.; Dietmayer, K. Probabilistic ego-motion estimation using multiple automotive radar sensors. Rob. Auton. Syst. 2017, 89, 136–146. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y.; Wang, Y.; Lin, Y.; Shen, W. The Millimeter-Wave Radar SLAM Assisted by the RCS Feature of the Target and IMU. Sensors 2020, 20, 5421. [Google Scholar] [CrossRef]
- Cen, S.H.; Newman, P. Precise Ego-Motion Estimation with Millimeter-Wave Radar Under Diverse and Challenging Conditions. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6045–6052. [Google Scholar]
- Cen, S.H.; Newman, P. Radar-only ego-motion estimation in difficult settings via graph matching. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 298–304. [Google Scholar]
- Vivet, D.; Checchin, P.; Chapuis, R. Localization and Mapping Using Only a Rotating FMCW Radar Sensor. Sensors 2013, 13, 4527–4552. [Google Scholar] [CrossRef]
- Burnett, K.; Schoellig, A.P.; Barfoot, T.D. Do We Need to Compensate for Motion Distortion and Doppler Effects in Spinning Radar Navigation? IEEE Rob. Autom. Lett. 2021, 6, 771–778. [Google Scholar] [CrossRef]
- Retan, K.; Loshaj, F.; Heizmann, M. Radar Odometry on SE(3) With Constant Velocity Motion Prior. IEEE Rob. Autom. Lett. 2021, 6, 6386–6393. [Google Scholar] [CrossRef]
- Zaffar, M.; Ehsan, S.; Stolkin, R.; Maier, K.M. Sensors, SLAM and Long-term Autonomy: A Review. In Proceedings of the NASA/ESA Conference on Adaptive Hardware and Systems (AHS), Edinburgh, UK, 6–9 August 2018; pp. 285–290. [Google Scholar]
- Fossum, E.R. The Invention of CMOS Image Sensors: A Camera in Every Pocket. In Proceedings of the Pan Pacific Microelectronics Symposium (Pan Pacific), Kapaau, Hawaii, 10–13 February 2020; pp. 1–6. [Google Scholar]
- Jansen-van Vuuren, R.D.; Armin, A.; Pandey, A.K.; Burn, P.L.; Meredith, P. Organic Photodiodes: The Future of Full Color Detection and Image Sensing. Adv. Mater. 2016, 28, 4766–4802. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, C.; Niu, L.; Zhang, X.; Zhang, F. Recent Progress on Broadband Organic Photodetectors and their Applications. Laser Photonics Rev. 2020, 14, 2000262. [Google Scholar] [CrossRef]
- Wang, Y.; Kublitski, J.; Xing, S.; Dollinger, F.; Spoltore, D.; Benduhn, J.; Leo, K. Narrowband organic photodetectors—Towards miniaturized, spectroscopic sensing. Mater. Horiz. 2022, 9, 220–251. [Google Scholar] [CrossRef]
- Hata, K.; Savarese, S. CS231A Course Notes 1: Camera Models. 2017. Available online: https://web.stanford.edu/class/cs231a/course_notes/01-camera-models.pdf (accessed on 1 March 2022).
- Peter, S.; Srikumar, R.; Simone, G.; João, B. Camera Models and Fundamental Concepts Used in Geometric Computer Vision. Found. Trends Comput. Graph. Vis. 2011, 6, 1–183. [Google Scholar]
- Corke, P.I.; Khatib, O. Robotics, Vision and Ccontrol: Fundamental Algorithms in MATLAB; Springer: Berlin/Heidelberg, Germany, 2011; Volume 73. [Google Scholar]
- Nister, D.; Naroditsky, O.; Bergen, J. Visual odometry. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; p. I. [Google Scholar]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Aqel, M.O.A.; Marhaban, M.H.; Saripan, M.I.; Ismail, N.B. Review of visual odometry: Types, approaches, challenges, and applications. SpringerPlus 2016, 5, 1897. [Google Scholar] [CrossRef] [Green Version]
- Poddar, S.; Kottath, R.; Karar, V. Motion Estimation Made Easy: Evolution and Trends in Visual Odometry. In Recent Advances in Computer Vision: Theories and Applications, Hassaballah, M., Hosny, K.M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 305–331. [Google Scholar]
- Woo, A.; Fidan, B.; Melek, W.W. Localization for Autonomous Driving. In Handbook of Position Location; Wiley-IEEE Press: Hoboken, NJ, USA, 2018; pp. 1051–1087. [Google Scholar]
- Scaramuzza, D.; Fraundorfer, F. Visual Odometry [Tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Fraundorfer, F.; Scaramuzza, D. Visual Odometry: Part II: Matching, Robustness, Optimization, and Applications. IEEE Robot. Autom. Mag. 2012, 19, 78–90. [Google Scholar] [CrossRef] [Green Version]
- Lim, K.L.; Bräunl, T. A Review of Visual Odometry Methods and Its Applications for Autonomous Driving. arXiv 2020, arXiv:2009.09193. [Google Scholar]
- Li, R.; Wang, S.; Gu, D. Ongoing Evolution of Visual SLAM from Geometry to Deep Learning: Challenges and Opportunities. Cogn. Comput. 2018, 10, 875–889. [Google Scholar] [CrossRef]
- Wang, K.; Ma, S.; Chen, J.; Ren, F.; Lu, J. Approaches Challenges and Applications for Deep Visual Odometry Toward to Complicated and Emerging Areas. IEEE Trans. Cogn. Dev. Syst. 2020, 14, 35–49. [Google Scholar] [CrossRef]
- Alkendi, Y.; Seneviratne, L.; Zweiri, Y. State of the Art in Vision-Based Localization Techniques for Autonomous Navigation Systems. IEEE Access 2021, 9, 76847–76874. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. BRIEF: Binary Robust Independent Elementary Features; Springer: Berlin/Heidelberg, Germany, 2010; pp. 778–792. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vision 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-Up Robust Features (SURF). Comput. Vision Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Hassaballah, M.; Abdelmgeid, A.A.; Alshazly, H.A. Image Features Detection, Description and Matching. In Image Feature Detectors and Descriptors: Foundations and Applications; Awad, A.I., Hassaballah, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 11–45. [Google Scholar]
- Li, Y.; Wang, S.; Tian, Q.; Ding, X. A survey of recent advances in visual feature detection. Neurocomputing 2015, 149, 736–751. [Google Scholar] [CrossRef]
- Pajdla, T. The Art of Solving Minimal Problems. Available online: http://cmp.felk.cvut.cz/minimal-iccv-2015/program.html (accessed on 1 March 2022).
- Hartley, R.I. In defense of the eight-point algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 580–593. [Google Scholar] [CrossRef] [Green Version]
- Hu, G.; Huang, S.; Zhao, L.; Alempijevic, A.; Dissanayake, G. A robust RGB-D SLAM algorithm. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 1714–1719. [Google Scholar]
- Geiger, A.; Ziegler, J.; Stiller, C. StereoScan: Dense 3d reconstruction in real-time. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 963–968. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Philip, J. A Non-Iterative Algorithm for Determining All Essential Matrices Corresponding to Five Point Pairs. Photogramm. Rec. 1996, 15, 589–599. [Google Scholar] [CrossRef]
- Pizarro, O.; Eustice, R.; Singh, H. Relative Pose Estimation for Instrumented, Calibrated Imaging Platforms; DICTA: Calgary, AB, Canada, 2003; pp. 601–612. [Google Scholar]
- Philip, J. Critical Point Configurations of the 5-, 6-, 7-, and 8-Point Algorithms for Relative Orientation; Department of Mathematics, Royal Institute of Technology: Stockholm, Sweden, 1998. [Google Scholar]
- Li, H. A Simple Solution to the Six-Point Two-View Focal-Length Problem; Springer: Berlin/Heidelberg, Germany, 2006; pp. 200–213. [Google Scholar]
- Hartley, R.; Li, H. An Efficient Hidden Variable Approach to Minimal-Case Camera Motion Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2303–2314. [Google Scholar] [CrossRef]
- Nister, D. An efficient solution to the five-point relative pose problem. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 756–770. [Google Scholar] [CrossRef] [PubMed]
- Hongdong, L.; Hartley, R. Five-Point Motion Estimation Made Easy. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Washington, DC, USA, 20–24 August 2006; pp. 630–633. [Google Scholar]
- Stewénius, H.; Engels, C.; Nistér, D. Recent developments on direct relative orientation. ISPRS J. Photogramm. Remote Sens. 2006, 60, 284–294. [Google Scholar] [CrossRef]
- Fathian, K.; Ramirez-Paredes, J.P.; Doucette, E.A.; Curtis, J.W.; Gans, N.R. QuEst: A Quaternion-Based Approach for Camera Motion Estimation From Minimal Feature Points. IEEE Rob. Autom. Lett. 2018, 3, 857–864. [Google Scholar] [CrossRef] [Green Version]
- Kukelova, Z.; Bujnak, M.; Pajdla, T. Polynomial Eigenvalue Solutions to the 5-pt and 6-pt Relative Pose Problems; BMVC: Columbus, OH, USA, 2008. [Google Scholar]
- Rodehorst, V.; Heinrichs, M.; Hellwich, O. Evaluation of relative pose estimation methods for multi-camera setups. Int. Arch. Photogramm. Remote Sens. 2008, XXXVII, 135–140. [Google Scholar]
- Li, B.; Heng, L.; Lee, G.H.; Pollefeys, M. A 4-point algorithm for relative pose estimation of a calibrated camera with a known relative rotation angle. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1595–1601. [Google Scholar]
- Fraundorfer, F.; Tanskanen, P.; Pollefeys, M. A Minimal Case Solution to the Calibrated Relative Pose Problem for the Case of Two Known Orientation Angles; Springer: Berlin/Heidelberg, Germany, 2010; pp. 269–282. [Google Scholar]
- Ding, Y.; Yang, J.; Kong, H. An efficient solution to the relative pose estimation with a common direction. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Virtual Conference, 31 May–31 August 2020; pp. 11053–11059. [Google Scholar]
- Scaramuzza, D. Performance evaluation of 1-point-RANSAC visual odometry. J. Field Rob. 2011, 28, 792–811. [Google Scholar] [CrossRef]
- Saurer, O.; Vasseur, P.; Boutteau, R.; Demonceaux, C.; Pollefeys, M.; Fraundorfer, F. Homography Based Egomotion Estimation with a Common Direction. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 327–341. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choi, S.; Kim, J.-H. Fast and reliable minimal relative pose estimation under planar motion. Image Vision Comput. 2018, 69, 103–112. [Google Scholar] [CrossRef]
- Pan, S.; Wang, X. A Survey on Perspective-n-Point Problem. In Proceedings of the 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 2396–2401. [Google Scholar]
- Haralick, B.M.; Lee, C.-N.; Ottenberg, K.; Nölle, M. Review and analysis of solutions of the three point perspective pose estimation problem. Int. J. Comput. Vision 1994, 13, 331–356. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, Z. Why is the Danger Cylinder Dangerous in the P3P Problem? Acta Autom. Sin. 2006, 32, 504. [Google Scholar]
- Xiao-Shan, G.; Xiao-Rong, H.; Jianliang, T.; Hang-Fei, C. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar] [CrossRef]
- Persson, M.; Nordberg, K. Lambda Twist: An Accurate Fast Robust Perspective Three Point (P3P) Solver; Springer: Cham, Switzerland, 2018; pp. 334–349. [Google Scholar]
- Kneip, L.; Scaramuzza, D.; Siegwart, R. A novel parametrization of the perspective-three-point problem for a direct computation of absolute camera position and orientation. In Proceedings of the CVPR, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2969–2976. [Google Scholar]
- Ke, T.; Roumeliotis, S.I. An Efficient Algebraic Solution to the Perspective-Three-Point Problem. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4618–4626. [Google Scholar]
- Lu, C.; Hager, G.D.; Mjolsness, E. Fast and globally convergent pose estimation from video images. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 610–622. [Google Scholar] [CrossRef] [Green Version]
- Garro, V.; Crosilla, F.; Fusiello, A. Solving the PnP Problem with Anisotropic Orthogonal Procrustes Analysis. In Proceedings of the Second International Conference on 3D Imaging Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012; pp. 262–269. [Google Scholar]
- Terzakis, G.; Lourakis, M. A Consistently Fast and Globally Optimal Solution to the Perspective-n-Point Problem; Springer: Cham, Switzerland, 2020; pp. 478–494. [Google Scholar]
- Lepetit, V.; Moreno-Noguer, F.; Fua, P. EPnP: An Accurate O(n) Solution to the PnP Problem. Int. J. Comput. Vision 2008, 81, 155. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Xu, C.; Xie, M. A Robust O(n) Solution to the Perspective-n-Point Problem. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1444–1450. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xu, G.; Cheng, Y.; Yu, Q. A simple, robust and fast method for the perspective-n-point Problem. Pattern Recognit. Lett. 2018, 108, 31–37. [Google Scholar] [CrossRef]
- Hesch, J.A.; Roumeliotis, S.I. A Direct Least-Squares (DLS) method for PnP. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–3 November 2011; pp. 383–390. [Google Scholar]
- Zheng, Y.; Kuang, Y.; Sugimoto, S.; Åström, K.; Okutomi, M. Revisiting the PnP Problem: A Fast, General and Optimal Solution. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2344–2351. [Google Scholar]
- Whelan, T.; Johannsson, H.; Kaess, M.; Leonard, J.J.; McDonald, J. Robust real-time visual odometry for dense RGB-D mapping. In Proceedings of the IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 5724–5731. [Google Scholar]
- Andreasson, H.; Stoyanov, T. Real time registration of RGB-D data using local visual features and 3D-NDT registration. In Proceedings of the SPME Workshop at Int. Conf. on Robotics and Automation (ICRA), St Paul, MN, USA, 14–19 May 2012. [Google Scholar]
- Zeisl, B.; Köser, K.; Pollefeys, M. Automatic Registration of RGB-D Scans via Salient Directions. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2808–2815. [Google Scholar]
- Fang, Z.; Scherer, S. Experimental study of odometry estimation methods using RGB-D cameras. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 680–687. [Google Scholar]
- 214. Vicente, M.-G.; Marcelo, S.-C.; Victor, V.-M.; Jorge, A.-L.; Jose, G.-R.; Miguel, C.; Sergio, O.-E.; Andres, F.-G. A Survey of 3D Rigid Registration Methods for RGB-D Cameras. In Advancements in Computer Vision and Image Processing; Jose, G.-R., Ed.; IGI Global: Hershey, PA, USA, 2018; pp. 74–98. [Google Scholar]
- Comport, A.I.; Malis, E.; Rives, P. Real-time Quadrifocal Visual Odometry. Int. J. Robot. Res. 2010, 29, 245–266. [Google Scholar] [CrossRef] [Green Version]
- Engel, J.; Stückler, J.; Cremers, D. Large-scale direct SLAM with stereo cameras. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 1935–1942. [Google Scholar]
- Wang, Z.; Li, M.; Zhou, D.; Zheng, Z. Direct Sparse Stereo Visual-Inertial Global Odometry. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hybrid Event, 30 May–5 June 2021; pp. 14403–14409. [Google Scholar]
- Liu, W.; Mohta, K.; Loianno, G.; Daniilidis, K.; Kumar, V. Semi-dense visual-inertial odometry and mapping for computationally constrained platforms. Auton. Robot. 2021, 45, 773–787. [Google Scholar] [CrossRef]
- Whelan, T.; Salas-Moreno, R.F.; Glocker, B.; Davison, A.J.; Leutenegger, S. ElasticFusion: Real-time dense SLAM and light source estimation. Int. J. Robot. Res. 2016, 35, 1697–1716. [Google Scholar] [CrossRef] [Green Version]
- Newcombe, R.A.; Lovegrove, S.J.; Davison, A.J. DTAM: Dense tracking and mapping in real-time. In Proceedings of the International Conference on Computer Vision, Washington, DC, USA, 6–13 November 2011; pp. 2320–2327. [Google Scholar]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM; Springer: Cham, Switzerland, 2014; pp. 834–849. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct Sparse Odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 611–625. [Google Scholar] [CrossRef]
- Zubizarreta, J.; Aguinaga, I.; Montiel, J.M.M. Direct Sparse Mapping. IEEE Trans. Robot. 2020, 36, 1363–1370. [Google Scholar] [CrossRef]
- Jaegle, A.; Phillips, S.; Daniilidis, K. Fast, robust, continuous monocular egomotion computation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 773–780. [Google Scholar]
- Raudies, F.; Neumann, H. A review and evaluation of methods estimating ego-motion. Comput. Vision Image Underst. 2012, 116, 606–633. [Google Scholar] [CrossRef]
- Forster, C.; Zhang, Z.; Gassner, M.; Werlberger, M.; Scaramuzza, D. SVO: Semidirect Visual Odometry for Monocular and Multicamera Systems. IEEE Trans. Robot. 2017, 33, 249–265. [Google Scholar] [CrossRef] [Green Version]
- Krombach, N.; Droeschel, D.; Behnke, S. Combining Feature-Based and Direct Methods for Semi-Dense Real-Time Stereo Visual Odometry; Springer: Cham, Switzerland, 2017; pp. 855–868. [Google Scholar]
- Luo, H.; Pape, C.; Reithmeier, E. Hybrid Monocular SLAM Using Double Window Optimization. IEEE Rob. Autom. Lett. 2021, 6, 4899–4906. [Google Scholar] [CrossRef]
- Lee, S.H.; Civera, J. Loosely-Coupled Semi-Direct Monocular SLAM. IEEE Rob. Autom. Lett. 2019, 4, 399–406. [Google Scholar] [CrossRef] [Green Version]
- Younes, G.; Asmar, D.; Zelek, J. A Unified Formulation for Visual Odometry*. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), The Venetian Macao, Macau, 3–8 November 2019; pp. 6237–6244. [Google Scholar]
- Introduction to Intel® RealSense™ Visual SLAM and the T265 Tracking Camera. Available online: https://dev.intelrealsense.com/docs/intel-realsensetm-visual-slam-and-the-t265-tracking-camera (accessed on 1 March 2022).
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klein, G.; Murray, D. Parallel Tracking and Mapping for Small AR Workspaces. In Proceedings of the 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, Nara, Japan, 13–16 November 2007; pp. 225–234. [Google Scholar]
- Pire, T.; Fischer, T.; Castro, G.; De Cristóforis, P.; Civera, J.; Jacobo Berlles, J. S-PTAM: Stereo Parallel Tracking and Mapping. Rob. Auton. Syst. 2017, 93, 27–42. [Google Scholar] [CrossRef] [Green Version]
- Ng, T.N.; Wong, W.S.; Chabinyc, M.L.; Sambandan, S.; Street, R.A. Flexible image sensor array with bulk heterojunction organic photodiode. Appl. Phys. Lett. 2008, 92, 213303. [Google Scholar] [CrossRef]
- Gallego, G.; Delbrück, T.; Orchard, G.; Bartolozzi, C.; Taba, B.; Censi, A.; Leutenegger, S.; Davison, A.J.; Conradt, J.; Daniilidis, K.; et al. Event-Based Vision: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 154–180. [Google Scholar] [CrossRef]
- Posch, C.; Serrano-Gotarredona, T.; Linares-Barranco, B.; Delbruck, T. Retinomorphic Event-Based Vision Sensors: Bioinspired Cameras With Spiking Output. Proc. IEEE 2014, 102, 1470–1484. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Gallego, G.; Shen, S. Event-Based Stereo Visual Odometry. IEEE Trans. Robot. 2021, 37, 1433–1450. [Google Scholar] [CrossRef]
- Martin, A.; Dodane, D.; Leviandier, L.; Dolfi, D.; Naughton, A.; O’Brien, P.; Spuessens, T.; Baets, R.; Lepage, G.; Verheyen, P.; et al. Photonic Integrated Circuit-Based FMCW Coherent LiDAR. J. Lightw. Technol. 2018, 36, 4640–4645. [Google Scholar] [CrossRef]
- Crouch, S. Advantages of 3D imaging coherent lidar for autonomous driving applications. In Proceedings of the 19th Coherent Laser Radar Conference, Okinawa, Japan, 18–21 June 2018; pp. 18–21. [Google Scholar]
- Zhang, X.; Kwon, K.; Henriksson, J.; Luo, J.; Wu, M.C. A large-scale microelectromechanical-systems-based silicon photonics LiDAR. Nature 2022, 603, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. DeepVO: Towards end-to-end visual odometry with deep Recurrent Convolutional Neural Networks. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 2043–2050. [Google Scholar]
- Yang, N.; Stumberg, L.v.; Wang, R.; Cremers, D. D3VO: Deep Depth, Deep Pose and Deep Uncertainty for Monocular Visual Odometry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1278–1289. [Google Scholar]
- Brossard, M.; Bonnabel, S.; Barrau, A. Denoising IMU Gyroscopes With Deep Learning for Open-Loop Attitude Estimation. IEEE Rob. Autom. Lett. 2020, 5, 4796–4803. [Google Scholar] [CrossRef]
- Burnett, K.; Yoon, D.J.; Schoellig, A.P.; Barfoot, T.D. Radar odometry combining probabilistic estimation and unsupervised feature learning. arXiv 2021, arXiv:2105.14152. [Google Scholar]
- Li, Q.; Chen, S.; Wang, C.; Li, X.; Wen, C.; Cheng, M.; Li, J. LO-Net: Deep Real-Time Lidar Odometry. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8465–8474. [Google Scholar]
- Brossard, M.; Barrau, A.; Bonnabel, S. AI-IMU Dead-Reckoning. IEEE Trans. Intell. Veh. 2020, 5, 585–595. [Google Scholar] [CrossRef]
- Hu, J.-W.; Zheng, B.-Y.; Wang, C.; Zhao, C.-H.; Hou, X.-L.; Pan, Q.; Xu, Z. A survey on multi-sensor fusion based obstacle detection for intelligent ground vehicles in off-road environments. Front. Inf. Technol. Electron. Eng. 2020, 21, 675–692. [Google Scholar] [CrossRef]
- Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Galar, D.; Kumar, U. Chapter 1—Sensors and Data Acquisition. In eMaintenance; Galar, D., Kumar, U., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 1–72. [Google Scholar]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Qu, Y.; Yang, M.; Zhang, J.; Xie, W.; Qiang, B.; Chen, J. An Outline of Multi-Sensor Fusion Methods for Mobile Agents Indoor Navigation. Sensors 2021, 21, 1605. [Google Scholar] [CrossRef]
- Ho, T.S.; Fai, Y.C.; Ming, E.S.L. Simultaneous localization and mapping survey based on filtering techniques. In Proceedings of the 10th Asian Control Conference (ASCC), Sabah, Malaysia, 31 May–3 June 2015; pp. 1–6. [Google Scholar]
- Grisetti, G.; Kümmerle, R.; Stachniss, C.; Burgard, W. A Tutorial on Graph-Based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, B.; Wu, C.; Guo, Y.; Li, L. Factor graph based navigation and positioning for control system design: A review. Chin. J. Aeronaut. 2021, 35, 25–39. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics (Intelligent Robotics and Autonomous Agents); MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Bloesch, M.; Omari, S.; Hutter, M.; Siegwart, R. Robust visual inertial odometry using a direct EKF-based approach. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 298–304. [Google Scholar]
- Xu, W.; Zhang, F. FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter. IEEE Rob. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Huang, G. Visual-Inertial Navigation: A Concise Review. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, Canada, 20–24 May 2019; pp. 9572–9582. [Google Scholar]
- Brossard, M.; Bonnabel, S.; Barrau, A. Unscented Kalman Filter on Lie Groups for Visual Inertial Odometry. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 649–655. [Google Scholar]
- Sun, K.; Mohta, K.; Pfrommer, B.; Watterson, M.; Liu, S.; Mulgaonkar, Y.; Taylor, C.J.; Kumar, V. Robust Stereo Visual Inertial Odometry for Fast Autonomous Flight. IEEE Rob. Autom. Lett. 2018, 3, 965–972. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Mourikis, A.I. High-precision, consistent EKF-based visual-inertial odometry. Int. J. Robot. Res. 2013, 32, 690–711. [Google Scholar] [CrossRef]
- Bloesch, M.; Burri, M.; Omari, S.; Hutter, M.; Siegwart, R. Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback. Int. J. Robot. Res. 2017, 36, 1053–1072. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.; Mann, G.K.I.; Vardy, A.; Gosine, R.G. Developing Computationally Efficient Nonlinear Cubature Kalman Filtering for Visual Inertial Odometry. J. Dyn. Syst. Meas. Contr. 2019, 141, 081012. [Google Scholar] [CrossRef]
- Zhu, J.; Tang, Y.; Shao, X.; Xie, Y. Multisensor Fusion Using Fuzzy Inference System for a Visual-IMU-Wheel Odometry. IEEE Trans. Instrum. Meas. 2021, 70, 3051999. [Google Scholar] [CrossRef]
- Li, L.; Yang, M. Joint Localization Based on Split Covariance Intersection on the Lie Group. IEEE Trans. Robot. 2021, 37, 1508–1524. [Google Scholar] [CrossRef]
- Barrau, A.; Bonnabel, S. Invariant Kalman Filtering. Annu. Rev. Control Rob. Auton. Syst. 2018, 1, 237–257. [Google Scholar] [CrossRef]
- Hartig, F.; Calabrese, J.M.; Reineking, B.; Wiegand, T.; Huth, A. Statistical inference for stochastic simulation models—Theory and application. Ecol. Lett. 2011, 14, 816–827. [Google Scholar] [CrossRef]
- Elfring, J.; Torta, E.; van de Molengraft, R. Particle Filters: A Hands-On Tutorial. Sensors 2021, 21, 438. [Google Scholar] [CrossRef]
- Doucet, A.; Freitas, N.D.; Murphy, K.P.; Russell, S.J. Rao-Blackwellised Particle Filtering for Dynamic Bayesian Networks. In Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence, San Francisco, CA, USA, 30 June–3 July 2000; pp. 176–183. [Google Scholar]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved Techniques for Grid Mapping With Rao-Blackwellized Particle Filters. IEEE Trans. Robot. 2007, 23, 34–46. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.-B.; Wang, P.; Chen, Z.-H. An improved particle filter for mobile robot localization based on particle swarm optimization. Expert Syst. Appl. 2019, 135, 181–193. [Google Scholar] [CrossRef]
- Kim, H.; Liu, B.; Goh, C.Y.; Lee, S.; Myung, H. Robust Vehicle Localization Using Entropy-Weighted Particle Filter-based Data Fusion of Vertical and Road Intensity Information for a Large Scale Urban Area. IEEE Rob. Autom. Lett. 2017, 2, 1518–1524. [Google Scholar] [CrossRef]
- Jo, H.; Cho, H.M.; Jo, S.; Kim, E. Efficient Grid-Based Rao–Blackwellized Particle Filter SLAM With Interparticle Map Sharing. IEEE/ASME Trans. Mechatron. 2018, 23, 714–724. [Google Scholar] [CrossRef]
- Deng, X.; Mousavian, A.; Xiang, Y.; Xia, F.; Bretl, T.; Fox, D. PoseRBPF: A Rao–Blackwellized Particle Filter for 6-D Object Pose Tracking. IEEE Trans. Robot. 2021, 37, 1328–1342. [Google Scholar] [CrossRef]
- Zadeh, L.A. A Simple View of the Dempster-Shafer Theory of Evidence and Its Implication for the Rule of Combination. AI Mag. 1986, 7, 85. [Google Scholar] [CrossRef]
- Aggarwal, P.; Bhatt, D.; Devabhaktuni, V.; Bhattacharya, P. Dempster Shafer neural network algorithm for land vehicle navigation application. Inf. Sci. 2013, 253, 26–33. [Google Scholar] [CrossRef]
- Wang, D.; Xu, X.; Yao, Y.; Zhang, T. Virtual DVL Reconstruction Method for an Integrated Navigation System Based on DS-LSSVM Algorithm. IEEE Trans. Instrum. Meas. 2021, 70, 3063771. [Google Scholar] [CrossRef]
- Steyer, S.; Tanzmeister, G.; Wollherr, D. Grid-Based Environment Estimation Using Evidential Mapping and Particle Tracking. IEEE Trans. Intell. Veh. 2018, 3, 384–396. [Google Scholar] [CrossRef] [Green Version]
- Leung, K.Y.K.; Inostroza, F.; Adams, M. Relating Random Vector and Random Finite Set Estimation in Navigation, Mapping, and Tracking. IEEE Trans. Signal Process. 2017, 65, 4609–4623. [Google Scholar] [CrossRef]
- Mahler, R.P.S. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Zhang, F.; Stähle, H.; Gaschler, A.; Buckl, C.; Knoll, A. Single camera visual odometry based on Random Finite Set Statistics. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 559–566. [Google Scholar]
- Gao, L.; Battistelli, G.; Chisci, L. PHD-SLAM 2.0: Efficient SLAM in the Presence of Missdetections and Clutter. IEEE Trans. Robot. 2021, 37, 1834–1843. [Google Scholar] [CrossRef]
- Nannuru, S.; Blouin, S.; Coates, M.; Rabbat, M. Multisensor CPHD filter. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1834–1854. [Google Scholar] [CrossRef] [Green Version]
- Fröhle, M.; Lindberg, C.; Granström, K.; Wymeersch, H. Multisensor Poisson Multi-Bernoulli Filter for Joint Target–Sensor State Tracking. IEEE Trans. Intell. Veh. 2019, 4, 609–621. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Hou, C.; Yi, D. Multi-Bernoulli smoother for multi-target tracking. Aerosp. Sci. Technol. 2016, 48, 234–245. [Google Scholar] [CrossRef]
- Jurić, A.; Kendeš, F.; Marković, I.; Petrović, I. A Comparison of Graph Optimization Approaches for Pose Estimation in SLAM. In Proceedings of the 44th International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 27 September–1 October 2021; pp. 1113–1118. [Google Scholar]
- Grisetti, G.; Guadagnino, T.; Aloise, I.; Colosi, M.; Della Corte, B.; Schlegel, D. Least Squares Optimization: From Theory to Practice. Robotics 2020, 9, 51. [Google Scholar] [CrossRef]
- Qin, C.; Ye, H.; Pranata, C.E.; Han, J.; Zhang, S.; Liu, M. LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Virtual, 31 May–31 August 2020; pp. 8899–8906. [Google Scholar]
- Zhang, J.; Singh, S. Laser–visual–inertial odometry and mapping with high robustness and low drift. J. Field Rob. 2018, 35, 1242–1264. [Google Scholar] [CrossRef]
- Zuo, X.; Geneva, P.; Lee, W.; Liu, Y.; Huang, G. LIC-Fusion: LiDAR-Inertial-Camera Odometry. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Venetian Macao, Macau, 3–8 November 2019; pp. 5848–5854. [Google Scholar]
- Montemerlo, M.; Thrun, S.; Roller, D.; Wegbreit, B. FastSLAM 2.0: An improved particle filtering algorithm for simultaneous localization and mapping that provably converges. In Proceedings of the 18th international joint conference on Artificial intelligence, Acapulco, Mexico, 9–15 August 2003; pp. 1151–1156. [Google Scholar]
- Leutenegger, S.; Lynen, S.; Bosse, M.; Siegwart, R.; Furgale, P. Keyframe-based visual–inertial odometry using nonlinear optimization. Int. J. Robot. Res. 2015, 34, 314–334. [Google Scholar] [CrossRef] [Green Version]
- Qin, T.; Li, P.; Shen, S. VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef] [Green Version]
- Rosinol, A.; Abate, M.; Chang, Y.; Carlone, L. Kimera: An Open-Source Library for Real-Time Metric-Semantic Localization and Mapping. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Virtual Conference, 31 May–31 August 2020; pp. 1689–1696. [Google Scholar]
- Ye, H.; Chen, Y.; Liu, M. Tightly Coupled 3D Lidar Inertial Odometry and Mapping. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, Canada, 20–24 May 2019; pp. 3144–3150. [Google Scholar]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October–24 January 2020; pp. 5135–5142. [Google Scholar]
- Shan, T.; Englot, B.; Ratti, C.; Rus, D. LVI-SAM: Tightly-coupled Lidar-Visual-Inertial Odometry via Smoothing and Mapping. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hybrid Event, 30 May–5 June 2021; pp. 5692–5698. [Google Scholar]
- Valente, M.; Joly, C.; Fortelle, A.D.L. Deep Sensor Fusion for Real-Time Odometry Estimation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Venetian Macao, Macau, 3–8 November 2019; pp. 6679–6685. [Google Scholar]
- Han, L.; Lin, Y.; Du, G.; Lian, S. DeepVIO: Self-supervised Deep Learning of Monocular Visual Inertial Odometry using 3D Geometric Constraints. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Venetian Macao, Macau, 3–8 November 2019; pp. 6906–6913. [Google Scholar]
- Wang, H.; Totaro, M.; Beccai, L. Toward Perceptive Soft Robots: Progress and Challenges. Adv. Sci. 2018, 5, 1800541. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Hughes, J.; Georgopoulou, A.; Clemens, F.; Iida, F. Using Redundant and Disjoint Time-Variant Soft Robotic Sensors for Accurate Static State Estimation. IEEE Rob. Autom. Lett. 2021, 6, 2099–2105. [Google Scholar] [CrossRef]
- Kim, D.; Park, M.; Park, Y.L. Probabilistic Modeling and Bayesian Filtering for Improved State Estimation for Soft Robots. IEEE Trans. Robot. 2021, 37, 1728–1741. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Shih, B.; Laschi, C.; Tolley, M.T. Soft robot perception using embedded soft sensors and recurrent neural networks. Sci. Rob. 2019, 4, eaav1488. [Google Scholar] [CrossRef] [PubMed]
- Drotman, D.; Jadhav, S.; Karimi, M.; Zonia, P.D.; Tolley, M.T. 3D printed soft actuators for a legged robot capable of navigating unstructured terrain. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5532–5538. [Google Scholar]
- Turan, M.; Almalioglu, Y.; Araujo, H.; Konukoglu, E.; Sitti, M. Deep EndoVO: A recurrent convolutional neural network (RCNN) based visual odometry approach for endoscopic capsule robots. Neurocomputing 2018, 275, 1861–1870. [Google Scholar] [CrossRef]
- Saeedi, S.; Trentini, M.; Seto, M.; Li, H. Multiple-Robot Simultaneous Localization and Mapping: A Review. J. Field Rob. 2016, 33, 3–46. [Google Scholar] [CrossRef]
- Weinstein, A.; Cho, A.; Loianno, G.; Kumar, V. Visual Inertial Odometry Swarm: An Autonomous Swarm of Vision-Based Quadrotors. IEEE Rob. Autom. Lett. 2018, 3, 1801–1807. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, Y.; Zhou, B.; Wang, L.; Yao, X.; Meng, G.; Shen, S. Omni-swarm: A Decentralized Omnidirectional Visual-Inertial-UWB State Estimation System for Aerial Swarm. arXiv 2021, arXiv:2103.04131. [Google Scholar]
- Bose, L.; Chen, J.; Carey, S.J.; Dudek, P.; Mayol-Cuevas, W. Visual Odometry for Pixel Processor Arrays. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4614–4622. [Google Scholar]




| Reference | Remarks |
|---|---|
| Bresson et al. [6] 2017 | SLAM in autonomous driving |
| Mohamed et al. [7] 2019 | Odometry systems |
| Huang et al. [8] 2020 | Representative LiDAR and visual SLAM systems dictionary |
| Chen et al. [9] 2020 Fayyad et al. [10] 2020 | Deep learning for localization and mapping |
| Yeong et al. [11] 2021 | Sensor and sensor calibration methods for robot perception |
| El-Sheimy et al. [1] 2021 | Overview of indoor navigation |
| Taheri et al. [12] 2021 | Chronicles of SLAM from 1986–2019 |
| Servières et al. [13] 2021 | Visual and visual-inertial odometry and SLAM |
| Category | Method | Automotive Radar (A)/Spinning Radar (S) | Radar Signal Representation | Loop-Closure |
|---|---|---|---|---|
| Direct methods | Fourier–Mellin transform [123] | S | Radar image | Yes |
| Doppler-effect-based [126] | A | Point cloud | No | |
| Indirect methods | Descriptor [137] | S | Radar image | Yes |
| ICP [139] | A | Point cloud | No | |
| NDT [140] | Both | Point cloud | No | |
| GMM [141] | A | Point cloud | No | |
| Graph-matching [144] | S | Radar image | No | |
| Distortion resolver [145] | S | Radar image | No | |
| Hybrid methods | RADARODO [130] | A | Radar image | No |
| SE(3) RO [147] | A | Point cloud | No |
| Category | Implementation | Camera Type | Loop-Closure | Remark |
|---|---|---|---|---|
| Feature-based | MonoSLAM [232] | Mono | No | |
| PTAM [233] | Mono | No | 5-point initiation | |
| S-PTAM [234] | Stereo | Yes | ||
| ORB-SLAM3 [157] | Mono/Stereo | Yes | PnP re-localization | |
| Appearance-based | DTAM [220] | Mono | No | Dense |
| LSD-SLAM [221] | Mono | Yes | Semi-dense | |
| DSO [222] | Mono | No | Sparse | |
| Hybrid | SVO [226] | Mono | No |
| Sensor | Material | Major Role(s) | Merit(s) Comparing with Non-Polymeric Counterparts |
|---|---|---|---|
| Accelerometer | SU-8 [20] | Proof mass and flexure | Low Young’s modulus and high sensitivity |
| Not reported [21] | Optical waveguide | High sensitivity | |
| Gyroscope | PDMS [27] | Proof mass | Reduced driving force |
| Not reported [26] | Optical waveguide | Low cost | |
| LiDAR | Acrylate polymer [49] | Phase modulator and waveguide | High thermo-optic coefficients and low thermal conductivity |
| P(VDF-TrFE) [51] | Actuator | Low cost | |
| Radar | LCP [109] | Substrate | Low dielectric loss |
| PANI [108] | Antenna | Flexibility and conformality | |
| HDPE [107] | Waveguide | Flexibility | |
| Camera | MEHPPV:PCBM [235] | Photodetector | Wavelength tunability |
| Sensor | Best Reported Accuracy | Cost | Advantages | Disadvantages | |
|---|---|---|---|---|---|
| Translation Error | Rotation Error (deg/m) | ||||
| IMU | 0.97% 1 | 0.0023 1 | Low–high | Self-contained | Drift |
| LiDAR | 0.55% 2 | 0.0013 2 | Medium–high | High accuracy; dense point cloud | Large volume; sensitive to weather |
| Radar | 1.76% 3 | 0.005 3 | Medium–high | Weatherproof; radial velocity measurement | Sparse point cloud; high noise level |
| Camera | 0.53% 2 | 0.0009 2 | Low–medium | Rich color information; compact | Sensitive to illumination; ambiguity in scale (monocular camera) |
| Method | Implementation and Year | Loosely Coupled/Tightly Coupled | Sensor Suite 1 | Loop-Closure | ||
|---|---|---|---|---|---|---|
| Filter-based | Probability-theory-based | Kalman filter | MSCKF [262], 2013 | T | V-I | No |
| ROVIO [257], 2015 | T | V-I | No | |||
| LINS [289], 2020 | T | L-I | No | |||
| FAST-LIO [258], 2020 | T | L-I | No | |||
| EKF RIO [128], 2020 | T | R-I | No | |||
| LVI-Odometry [290], 2018 | L | V-L-I | No | |||
| LIC fusion [291], 2019 | T | V-L-I | No | |||
| Particle filter | FastSLAM [292], 2002 | L-O | No | |||
| Evidential-reasoning-based | D–S combination | [277], 2013 | L | GPS-I | No | |
| Random-finite set-based | PHD filter | PHD-SLAM 2.0 [283], 2021 | T | L-O | No | |
| Optimization-based | OKVIS [293], 2014 | T | V-I | No | ||
| VINS-MONO [294], 2018 | T | V-I | Yes | |||
| Kimera [295], 2020 | T | V-I | Yes | |||
| LIO-mapping [296], 2019 | T | L-I | No | |||
| LIO-SAM [297], 2020 | T | L-I | Yes | |||
| LVI-SAM [298], 2021 | T | V-L-I | Yes | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Sun, X.; Jia, F.; Rushworth, A.; Dong, X.; Zhang, S.; Fang, Z.; Yang, G.; Liu, B. Sensors and Sensor Fusion Methodologies for Indoor Odometry: A Review. Polymers 2022, 14, 2019. https://doi.org/10.3390/polym14102019
Yang M, Sun X, Jia F, Rushworth A, Dong X, Zhang S, Fang Z, Yang G, Liu B. Sensors and Sensor Fusion Methodologies for Indoor Odometry: A Review. Polymers. 2022; 14(10):2019. https://doi.org/10.3390/polym14102019
Chicago/Turabian StyleYang, Mengshen, Xu Sun, Fuhua Jia, Adam Rushworth, Xin Dong, Sheng Zhang, Zaojun Fang, Guilin Yang, and Bingjian Liu. 2022. "Sensors and Sensor Fusion Methodologies for Indoor Odometry: A Review" Polymers 14, no. 10: 2019. https://doi.org/10.3390/polym14102019
APA StyleYang, M., Sun, X., Jia, F., Rushworth, A., Dong, X., Zhang, S., Fang, Z., Yang, G., & Liu, B. (2022). Sensors and Sensor Fusion Methodologies for Indoor Odometry: A Review. Polymers, 14(10), 2019. https://doi.org/10.3390/polym14102019