Prediction of Thermal Conductivities of Rubbers by MD Simulations—New Insights
Abstract
:1. Introduction
2. Simulation Details
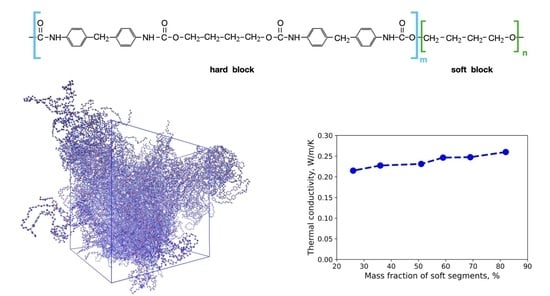
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dong, H.; Fan, Z.; Shi, L.; Harju, A.; Ala-Nissila, T. Equivalence of the equilibrium and the nonequilibrium molecular dynamics methods for thermal conductivity calculations: From bulk to nanowire silicon. Phys. Rev. B 2018, 97, 094305. [Google Scholar] [CrossRef] [Green Version]
- Kubo, R. Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 2002, 65, 144306. [Google Scholar] [CrossRef] [Green Version]
- Sellan, D.P.; Landry, E.S.; Turney, J.E.; McGaughey, A.J.H.; Amon, C.H. Size effects in molecular dynamics thermal conductivity predictions. Phys. Rev. B 2010, 81, 214305. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Kim, K.; Wang, Y.; Liu, J. Strain effects on the anisotropic thermal transport in crystalline polyethylene. Appl. Phys. Lett. 2018, 112, 051907. [Google Scholar] [CrossRef]
- Engelmann, S.; Meyer, J.; Hentschke, R. Computer simulation of thermal conductivity in vulcanized polyisoprene at variable strain and temperature. Phys. Rev. B 2017, 96, 054110. [Google Scholar] [CrossRef]
- Li, S.; Yu, X.; Bao, H.; Yang, N. High Thermal Conductivity of Bulk Epoxy Resin by Bottom-Up Parallel-Linking and Strain: A Molecular Dynamics Study. J. Phys. Chem. C 2018, 122, 13140–13147. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Ma, L.X.; Tang, Y.Z.; Wang, Z.P.; Li, W.; Kukulka, D. Thermal Conductivity of Natural Rubber Using Molecular Dynamics Simulation. J. Nanosci. Nanotechnol. 2015, 15, 3244–3248. [Google Scholar] [CrossRef]
- Huang, H.S.; Ganguli, S.; Roy, A.K. Prediction of the transverse thermal conductivity of pitch-based carbon fibers. J. Compos. Mater. 2014, 48, 1383–1390. [Google Scholar] [CrossRef]
- Vasilev, A.; Lorenz, T.; Kamble, V.G.; Wießner, S.; Breitkopf, C. Thermal Conductivity of Polybutadiene Rubber from Molecular Dynamics Simulations and Measurements by the Heat Flow Meter Method. Materials 2021, 14, 7737. [Google Scholar] [CrossRef]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]
- Eslami, H.; Mohammadzadeh, L.; Mehdipour, N. Anisotropic heat transport in nanoconfined polyamide-6, 6 oligomers: Atomistic reverse nonequilibrium molecular dynamics simulation. J. Chem. Phys. 2012, 136, 104901. [Google Scholar] [CrossRef]
- Zhang, M.; Lussetti, E.; de Souza, L.E.; Müller-Plathe, F. Thermal conductivities of molecular liquids by reverse nonequilibrium molecular dynamics. J. Phys. Chem. B 2005, 109, 15060–15067. [Google Scholar] [CrossRef]
- Müller-Plathe, F.; Bordat, P. Reverse non-equilibrium molecular dynamics. In Novel Methods in Soft Matter Simulations; Springer: Berlin/Heidelberg, Germany, 2004; pp. 310–326. [Google Scholar]
- Yang, H.A.; Cao, B.Y. Effects and correction of angular momentum non-conservation in RNEMD for calculating thermal conductivity. Comput. Mater. Sci. 2020, 183, 109753. [Google Scholar] [CrossRef]
- Ikeshoji, T.; Hafskjold, B. Non-equilibrium molecular dynamics calculation of heat conduction in liquid and through liquid-gas interface. Mol. Phys. 1994, 81, 251–261. [Google Scholar] [CrossRef]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302. [Google Scholar] [CrossRef]
- Algaer, E. Thermal Conductivity of Polymer Materials - Reverse Nonequilibrium Molecular Dynamics Simulations. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2010. [Google Scholar]
- Azizi, K.; Hirvonen, P.; Fan, Z.; Harju, A.; Elder, K.R.; Ala-Nissila, T.; Allaei, S.M.V. Kapitza thermal resistance across individual grain boundaries in graphene. Carbon 2017, 125, 384–390. [Google Scholar] [CrossRef] [Green Version]
- Liang, Z.; Keblinski, P. Finite-size effects on molecular dynamics interfacial thermal-resistance predictions. Phys. Rev. B 2014, 90, 075411. [Google Scholar] [CrossRef]
- Einalipour Eshkalak, K.; Sadeghzadeh, S.; Molaei, F. Interfacial thermal resistance mechanism for the polyaniline (C3N)–graphene heterostructure. J. Phys. Chem. C 2020, 124, 14316–14326. [Google Scholar] [CrossRef]
- Ju, S.H.; Liang, X.G. Investigation on interfacial thermal resistance and phonon scattering at twist boundary of silicon. J. Appl. Phys. 2013, 113, 053513. [Google Scholar] [CrossRef]
- Feng, T.; He, J.; Rai, A.; Hun, D.; Liu, J.; Shrestha, S.S. Size effects in the thermal conductivity of amorphous polymers. Phys. Rev. Appl. 2020, 14, 044023. [Google Scholar] [CrossRef]
- Wang, Y.; Gregory, C.; Minor, M.A. Improving mechanical properties of molded silicone rubber for soft robotics through fabric compositing. Soft Robot. 2018, 5, 272–290. [Google Scholar] [CrossRef] [PubMed]
- Nagaoka, T.; Mao, Z.; Takemura, K.; Yokota, S.; Kim, J.w. ECF (electro-conjugate fluid) finger with bidirectional motion and its application to a flexible hand. Smart Mater. Struct. 2019, 28, 025032. [Google Scholar] [CrossRef]
- Stokes, A.A.; Shepherd, R.F.; Morin, S.A.; Ilievski, F.; Whitesides, G.M. A hybrid combining hard and soft robots. Soft Robot. 2014, 1, 70–74. [Google Scholar] [CrossRef] [Green Version]
- Shapiro, Y.; Wolf, A.; Gabor, K. Bi-bellows: Pneumatic bending actuator. Sens. Actuators A Phys. 2011, 167, 484–494. [Google Scholar] [CrossRef]
- Xu, W.; Wu, Y.; Zhu, Y.; Liang, X.G. Molecular dynamics simulation of thermal conductivity of silicone rubber. Chin. Phys. B 2020, 29, 046601. [Google Scholar] [CrossRef]
- Kanan, A.; Vasilev, A.; Breitkopf, C.; Kaliske, M. Thermo-Electro-Mechanical Simulation of Electro-Active Composites. Materials 2022, 15, 783. [Google Scholar] [CrossRef]
- Katzer, K.; Kanan, A.; Pfeil, S.; Grellmann, H.; Gerlach, G.; Kaliske, M.; Cherif, C.; Zimmermann, M. Thermo-Electro-Mechanical Characterization of PDMS-Based Dielectric Elastomer Actuators. Materials 2021, 15, 221. [Google Scholar] [CrossRef]
- Pfeil, S.; Katzer, K.; Kanan, A.; Mersch, J.; Zimmermann, M.; Kaliske, M.; Gerlach, G. A biomimetic fish fin-like robot based on textile reinforced silicone. Micromachines 2020, 11, 298. [Google Scholar] [CrossRef] [Green Version]
- Talapatra, A.; Datta, D. Molecular dynamics simulation-based study on enhancing thermal properties of graphene-reinforced thermoplastic polyurethane nanocomposite for heat exchanger materials. In Inverse Heat Conduction and Heat Exchangers; IntechOpen: London, UK, 2019. [Google Scholar]
- Talapatra, A.; Datta, D. A molecular dynamics-based investigation on tribological properties of functionalized graphene reinforced thermoplastic polyurethane nanocomposites. Proc. Inst. Mech. Eng. Part J. Eng. Tribol. 2021, 235, 61–78. [Google Scholar] [CrossRef]
- Vasilev, A.; Lorenz, T.; Breitkopf, C. Thermal Conductivity of Polyisoprene and Polybutadiene from Molecular Dynamics Simulations and Transient Measurements. Polymers 2020, 12, 1081. [Google Scholar] [CrossRef]
- Jia, J.; Pu, J.H.; Liu, J.H.; Zhao, X.; Ke, K.; Bao, R.Y.; Liu, Z.Y.; Yang, M.B.; Yang, W. Surface structure engineering for a bionic fiber-based sensor toward linear, tunable, and multifunctional sensing. Mater. Horizons 2020, 7, 2450–2459. [Google Scholar] [CrossRef]
- Żur, A.; Żur, P.; Michalski, P.; Baier, A. Preliminary Study on Mechanical Aspects of 3D-Printed PLA-TPU Composites. Materials 2022, 15, 2364. [Google Scholar] [CrossRef]
- Jewett, A.I.; Zhuang, Z.; Shea, J.E. Moltemplate a coarse-grained model assembly tool. Biophys. J. 2013, 104, 169a. [Google Scholar] [CrossRef] [Green Version]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhou, T.; Li, L.; Zhang, J.; Liu, X.; Ke, X.; Zhang, A. Hydrogen bond breaking of TPU upon heating: Understanding from the viewpoints of molecular movements and enthalpy. RSC Adv. 2015, 5, 31153–31165. [Google Scholar] [CrossRef]
- Compute Heat/Flux Command. Available online: https://docs.lammps.org/compute_heat_flux.html (accessed on 16 May 2022).
- Xiong, X.; Yang, M.; Liu, C.; Li, X.; Tang, D. Thermal conductivity of cross-linked polyethylene from molecular dynamics simulation. J. Appl. Phys. 2017, 122, 035104. [Google Scholar] [CrossRef]
- Kikugawa, G.; Desai, T.G.; Keblinski, P.; Ohara, T. Effect of crosslink formation on heat conduction in amorphous polymers. J. Appl. Phys. 2013, 114, 034302. [Google Scholar] [CrossRef] [Green Version]
- Monk, J.D.; Bucholz, E.W.; Boghozian, T.; Deshpande, S.; Schieber, J.; Bauschlicher Jr, C.W.; Lawson, J.W. Computational and experimental study of phenolic resins: Thermal–mechanical properties and the role of hydrogen bonding. Macromolecules 2015, 48, 7670–7680. [Google Scholar] [CrossRef]
- Monk, J.D.; Haskins, J.B.; Bauschlicher Jr, C.W.; Lawson, J.W. Molecular dynamics simulations of phenolic resin: Construction of atomistic models. Polymer 2015, 62, 39–49. [Google Scholar] [CrossRef]
- Knappe, W.; Yamamoto, O. Effects of crosslinking and chain degradation on the thermal conductivity of polymers. Kolloid-Z. Und Z. FÜR Polym. 1970, 240, 775–783. [Google Scholar] [CrossRef]
- Yamamoto, O. Thermal conductivity of cross-linked polymers. Polym. J. 1971, 2, 509–517. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Feng, S.; Diao, G. Thermal conductivity of silicone rubber filled with ZnO. Polym. Compos. 2007, 28, 125–130. [Google Scholar] [CrossRef]
- Yeh, S.K.; Chen, Y.R.; Kang, T.W.; Tseng, T.J.; Peng, S.P.; Chu, C.C.; Rwei, S.P.; Guo, W.J. Different approaches for creating nanocellular TPU foams by supercritical CO2 foaming. J. Polym. Res. 2018, 25, 30. [Google Scholar] [CrossRef]
- Boubakri, A.; Guermazi, N.; Elleuch, K.; Ayedi, H. Study of UV-aging of thermoplastic polyurethane material. Mater. Sci. Eng. A 2010, 527, 1649–1654. [Google Scholar] [CrossRef]
- Li, X.; Wang, G.; Yang, C.; Zhao, J.; Zhang, A. Mechanical and EMI shielding properties of solid and microcellular TPU/nanographite composite membranes. Polym. Test. 2021, 93, 106891. [Google Scholar] [CrossRef]
- Sánchez-Calderón, I.; Bernardo, V.; Santiago-Calvo, M.; Naji, H.; Saiani, A.; Rodríguez-Pérez, M.Á. Effect of the Molecular Structure of TPU on the Cellular Structure of Nanocellular Polymers Based on PMMA/TPU Blends. Polymers 2021, 13, 3055. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, J.W.; Wei, N.; Zhang, Y.; Rabczuk, T. Thermal conductivity dependence on chain length in amorphous polymers. J. Appl. Phys. 2013, 113, 184304. [Google Scholar] [CrossRef]
- Ivan, K.; Pavol, K.; Jan, V.; Marta, H.; Zora, J. Temperature dependence of thermal properties of thermoplastic polyurethane-based carbon nanocomposites. In Proceedings of the AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; Volume 1768, p. 020019. [Google Scholar]








| Structure 1 | Structure 2 | Structure 3 | Structure 4 | Structure 5 | Structure 6 |
|---|---|---|---|---|---|
| 30 | 33 | 36 | 37 | 38 | 39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasilev, A.; Lorenz, T.; Breitkopf, C. Prediction of Thermal Conductivities of Rubbers by MD Simulations—New Insights. Polymers 2022, 14, 2046. https://doi.org/10.3390/polym14102046
Vasilev A, Lorenz T, Breitkopf C. Prediction of Thermal Conductivities of Rubbers by MD Simulations—New Insights. Polymers. 2022; 14(10):2046. https://doi.org/10.3390/polym14102046
Chicago/Turabian StyleVasilev, Aleksandr, Tommy Lorenz, and Cornelia Breitkopf. 2022. "Prediction of Thermal Conductivities of Rubbers by MD Simulations—New Insights" Polymers 14, no. 10: 2046. https://doi.org/10.3390/polym14102046
APA StyleVasilev, A., Lorenz, T., & Breitkopf, C. (2022). Prediction of Thermal Conductivities of Rubbers by MD Simulations—New Insights. Polymers, 14(10), 2046. https://doi.org/10.3390/polym14102046