Changes in the Local Conformational States Caused by Simple Na+ and K+ Ions in Polyelectrolyte Simulations: Comparison of Seven Force Fields with and without NBFIX and ECC Corrections
Abstract
:1. Introduction
2. Model, Force Fields and Method
2.1. Model
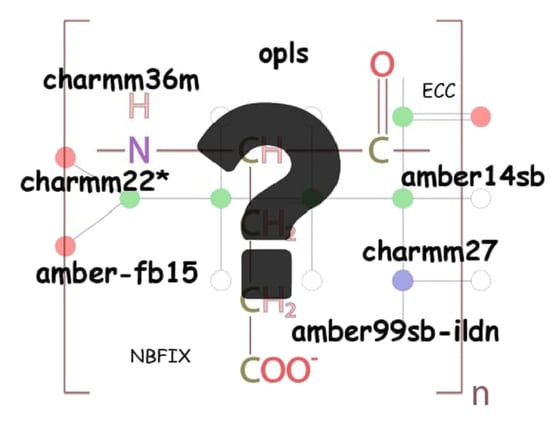
2.2. Force Fields
2.3. ECC and NBFIX Corrections in Protein-Ion Interactions
2.4. Method
3. Results
3.1. Ramachandran Maps and Backbone Conformations
3.2. Fractions of Major Backbone Conformations
3.2.1. Poly (Aspartic Acid)
3.2.2. Poly (Glutamic Acid)
3.3. Lengths of the Conformational Sequences in PASA and PGA
3.4. Correlations of Molecular Sizes (Rg) with Fractions of Stretched Monomer Conformations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cisneros, G.A.; Karttunen, M.; Ren, P.; Sagui, C. Classical electrostatics for biomolecular simulations. Chem. Rev. 2014, 114, 779–814. [Google Scholar] [CrossRef] [Green Version]
- Catte, A.; Girych, M.; Javanainen, M.; Loison, C.; Melcr, J.; Miettinen, M.S.; Monticelli, L.; Määttä, J.; Oganesyan, V.S.; Ollila, O.H.S.; et al. Molecular electrometer and binding of cations to phospholipid bilayers. Phys. Chem. Chem. Phys. 2016, 18, 32560–32569. [Google Scholar] [CrossRef] [Green Version]
- Yoo, J.; Aksimentiev, A. New tricks for old dogs: Improving the accuracy of biomolecular force fields by pair-specific corrections to non-bonded interactions. Phys. Chem. Chem. Phys. 2018, 20, 8432–8449. [Google Scholar] [CrossRef]
- Leontyev, I.V.; Stuchebrukhov, A.A. Electronic continuum model for molecular dynamics simulations of biological molecules. J. Chem. Theory Comput. 2010, 6, 1498–1508. [Google Scholar] [CrossRef]
- Melcr, J.; Martinez-Seara, H.; Nencini, R.; Kolafa, J.; Jungwirth, P.; Ollila, O.H.S. Accurate binding of sodium and calcium to a POPC bilayer by effective inclusion of electronic polarization. J. Phys. Chem. B 2018, 122, 4546–4557. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; MacKerell, A.D. CHARMM additive and polarizable force fields for biophysics and computer-aided drug design. Biochim. Biophys. Acta Gen. Subj. 2015, 1850, 861–871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopes, P.E.M.; Guvench, O.; MacKerell, A.D. Current status of protein force fields for molecular dynamics simulations. In Molecular Modeling of Proteins, 2nd ed.; Kukol, A., Ed.; Humana Press: New York, NY, USA, 2014; pp. 47–71. [Google Scholar] [CrossRef] [Green Version]
- Lemkul, J.A.; Huang, J.; Roux, B.; MacKerell, J.A.D. An empirical polarizable force field based on the classical drude oscillator model: Development history and recent applications. Chem. Rev. 2016, 116, 4983–5013. [Google Scholar] [CrossRef] [PubMed]
- Baker, C.M. Polarizable force fields for molecular dynamics simulations of biomolecules. WIREs Comput. Mol. Sci. 2015, 5, 241–254. [Google Scholar] [CrossRef]
- Jing, Z.; Liu, C.; Cheng, S.Y.; Qi, R.; Walker, B.D.; Piquemal, J.-P.; Ren, P. Polarizable force fields for biomolecular simulations: Recent advances and applications. Annu. Rev. Biophys. 2019, 48, 371–394. [Google Scholar] [CrossRef] [PubMed]
- Bedrov, D.; Piquemal, J.-P.; Borodin, O.; MacKerell, A.D.; Roux, B.; Schröder, C. Molecular dynamics simulations of ionic liquids and electrolytes using polarizable force fields. Chem. Rev. 2019, 119, 7940–7995. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Church, A.T.; Hughes, Z.E.; Walsh, T.R. Improving the description of interactions between Ca2+ and protein carboxylate groups, including γ-carboxyglutamic acid: Revised CHARMM22* parameters. RSC Adv. 2015, 5, 67820–67828. [Google Scholar] [CrossRef] [Green Version]
- Leontyev, I.; Stuchebrukhov, A. Accounting for electronic polarization in non-polarizable force fields. Phys. Chem. Chem. Phys. 2011, 13, 2613–2626. [Google Scholar] [CrossRef] [Green Version]
- Tolmachev, D.A.; Boyko, O.S.; Lukasheva, N.V.; Martinez-Seara, H.; Karttunen, M. Overbinding and qualitative and quantitative changes caused by simple Na+ and K+ Ions in polyelectrolyte simulations: Comparison of force fields with and without NBFIX and ECC corrections. J. Chem. Theory Comput. 2019, 16, 677–687. [Google Scholar] [CrossRef]
- Duboué-Dijon, E.; Javanainen, M.; Delcroix, P.; Jungwirth, P.; Martinez-Seara, H. A practical guide to biologically relevant molecular simulations with charge scaling for electronic polarization. J. Chem. Phys. 2020, 153, 050901. [Google Scholar] [CrossRef]
- Levin, Y. Electrostatic correlations: From plasma to biology. Rep. Prog. Phys. 2002, 65, 1577–1632. [Google Scholar] [CrossRef] [Green Version]
- Park, S.Y.; Bruinsma, R.F.; Gelbart, W.M. Spontaneous overcharging of macro-ion complexes. EPL Europhys. Lett. 1999, 46, 454–460. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marchand, G.; Soetens, J.-C.; Jacquemin, D.; Bopp, P.A. Effect of the cation model on the equilibrium structure of poly-L-glutamate in aqueous sodium chloride solution. J. Chem. Phys. 2015, 143, 224505. [Google Scholar] [CrossRef]
- Vitalini, F.; Noé, F.; Keller, B. Molecular dynamics simulations data of the twenty encoded amino acids in different force fields. Data Brief 2016, 7, 582–590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hollingsworth, S.A.; Karplus, P.A. A fresh look at the Ramachandran plot and the occurrence of standard structures in proteins. Biomol. Concepts 2010, 1, 271–283. [Google Scholar] [CrossRef]
- Jha, A.K.; Colubri, A.; Zaman, M.H.; Koide, S.; Sosnick, T.R.; Freed, K.F. Helix, sheet, and polyproline II frequencies and strong nearest neighbor effects in a restricted coil library. Biochemistry 2005, 44, 9691–9702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hagarman, A.; Measey, T.J.; Mathieu, D.; Schwalbe, H.; Schweitzer-Stenner, R. Intrinsic propensities of amino acid residues in GxG peptides inferred from Amide I′ band profiles and NMR scalar coupling constants. J. Am. Chem. Soc. 2010, 132, 540–551. [Google Scholar] [CrossRef] [PubMed]
- Grdadolnik, J.; Mohacek-Grosev, V.; Baldwin, R.L.; Avbelj, F. Populations of the three major backbone conformations in 19 amino acid dipeptides. Proc. Natl. Acad. Sci. USA 2011, 108, 1794–1798. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saudek, V.; Schmidt, P. Conformational study of poly(α-L-aspartic acid). Biopolymers 1982, 21, 1011–1020. [Google Scholar] [CrossRef]
- Gooding, E.A.; Sharma, S.; Petty, S.A.; Fouts, E.A.; Palmer, C.J.; Nolan, B.E.; Volk, M. pH-dependent helix folding dynamics of poly-glutamic acid. Chem. Phys. 2013, 422, 115–123. [Google Scholar] [CrossRef]
- Bordi, F.; Cametti, C.; Paradossi, G. Conformational transition in aqueous solution of poly(L-glutamic acid): A low-frequency electrical conductivity study. J. Phys. Chem. 1992, 96, 913–918. [Google Scholar] [CrossRef]
- Mikhonin, A.V.; Myshakina, N.S.; Bykov, A.S.V.; Asher, S.A. UV Resonance raman determination of polyproline II, extended 2.51-Helix, and β-Sheet Ψ angle energy landscape in Poly-l-Lysine and Poly-l-Glutamic acid. J. Am. Chem. Soc. 2005, 127, 7712–7720. [Google Scholar] [CrossRef]
- Whynes, R.; Volk, M.; Tavender, S.M.; Towrie, M. UV resonance Raman spectroscopy reveals details of the “random coil” state of polypeptides. Cent. Laser Facil. Annu. Rep. 2008, 169–172. [Google Scholar]
- Xiong, K.; Ma, L.; Asher, S.A. Conformation of poly-l-glutamate is independent of ionic strength. Biophys. Chem. 2012, 162, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Leontyev, I.V.; Stuchebrukhov, A.A. Electronic continuum model for molecular dynamics simulations. J. Chem. Phys. 2009, 130, 085102. [Google Scholar] [CrossRef] [Green Version]
- Terauchi, M.; Tamura, A.; Tonegawa, A.; Yamaguchi, S.; Yoda, T.; Yui, N. Polyelectrolyte complexes between Polycarboxylates and BMP-2 for Enhancing Osteogenic differentiation: Effect of chemical structure of Polycarboxylates. Polymers 2019, 11, 1327. [Google Scholar] [CrossRef] [Green Version]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.-P.; McKiernan, K.A.; Gomes, J.; Beauchamp, K.A.; Head-Gordon, T.; Rice, J.E.; Swope, W.C.; Martínez, T.J.; Pande, V.S. Building a more predictive protein force field: A systematic and reproducible route to AMBER-FB15. J. Phys. Chem. B 2017, 121, 4023–4039. [Google Scholar] [CrossRef]
- Mackerell, A.D., Jr.; Feig, M.; Brooks, C.L. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, G.N.M.; De Groot, B.L.; Grubmüller, H., Jr.; MacKerell, A.D. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piana, S.; Lindorff-Larsen, K.; Shaw, D.E. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 2011, 100, L47–L49. [Google Scholar] [CrossRef] [Green Version]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Wang, L.-P.; Martinez, T.J.; Pande, V.S. Building Force Fields: An Automatic, Systematic, and Reproducible Approach. J. Phys. Chem. Lett. 2014, 5, 1885–1891. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.L.; Dunbrack, R.L., Jr.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Yoo, J.; Aksimentiev, A. Improved parametrization of Li+, Na+, K+, and Mg2+ Ions for all-atom molecular dynamics simulations of nucleic acid systems. J. Phys. Chem. Lett. 2012, 3, 45–50. [Google Scholar] [CrossRef]
- Duboué-Dijon, E.; Delcroix, P.; Martinez-Seara, H.; Hladílková, J.; Coufal, P.; Křížek, T.; Jungwirth, P. Binding of divalent cations to insulin: Capillary electrophoresis and molecular simulations. J. Phys. Chem. B 2018, 122, 5640–5648. [Google Scholar] [CrossRef] [Green Version]
- Melcr, J.; Piquemal, J.-P. Accurate biomolecular simulations account for electronic polarization. Front. Mol. Biosci. 2019, 6, 143. [Google Scholar] [CrossRef] [Green Version]
- Kohagen, M.; Mason, P.; Jungwirth, P. Accounting for electronic polarization effects in Aqueous Sodium chloride via molecular dynamics aided by neutron scattering. J. Phys. Chem. B 2015, 120, 1454–1460. [Google Scholar] [CrossRef]
- Kohagen, M.; Mason, P.; Jungwirth, P. Accurate description of calcium solvation in concentrated aqueous solutions. J. Phys. Chem. B 2014, 118, 7902–7909. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 2002, 100, 191–198. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Jephthah, S.; Pesce, F.; Lindorff-Larsen, K.; Skepö, M. Force field effects in simulations of flexible peptides with varying Polyproline II propensity. J. Chem. Theory Comput. 2021, 17, 6634–6646. [Google Scholar] [CrossRef] [PubMed]
- Enkhbayar, P.; Hikichi, K.; Osaki, M.; Kretsinger, R.H.; Matsushima, N. 310-helices in proteins are parahelices. Proteins Struct. Funct. Bioinform. 2006, 64, 691–699. [Google Scholar] [CrossRef]
- Batys, P.; Morga, M.; Bonarek, P.; Sammalkorpi, M. pH-induced changes in Polypeptide conformation: Force-field comparison with experimental validation. J. Phys. Chem. B 2020, 124, 2961–2972. [Google Scholar] [CrossRef]
- Wang, D.; Marszalek, P.E. Exploiting a mechanical perturbation of a titin domain to identify how force field parameterization affects protein refolding pathways. J. Chem. Theory Comput. 2020, 16, 3240–3252. [Google Scholar] [CrossRef] [PubMed]
- Gopal, S.M.; Wingbermühle, S.; Schnatwinkel, J.; Juber, S.; Herrmann, C.; Schäfer, L.V. Conformational preferences of an intrinsically disordered protein domain: A case study for modern force fields. J. Phys. Chem. B 2021, 125, 24–35. [Google Scholar] [CrossRef] [PubMed]
- Fersht, A. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding, 1st ed.; W. H. Freeman: New York, NY, USA, 1998; Volume 9, ISBN 978-0716732686. [Google Scholar]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Fuxreiter, M. Computational Approaches to Protein Dynamics: From Quantum to Coarse-Grained Methods (Series in Computational Biophysics), 1st ed.; CRC Press: Abingdon, UK, 2014; ISBN 978-1466561571. [Google Scholar]













| Conformation | [23] | [24] | [29] | [57] | |||
|---|---|---|---|---|---|---|---|
| GA | di-ASA | di-GA | PGA | PGA | |||
| N, I | N | I | N | I | I | I | |
| PPII-helix | 0.54 | 0.43 | 0.49 | 0.59 | 0.47 | 0.40 | - |
| β-sheet | 0.26 | 0.55 | 0.46 | 0.36 | 0.48 | - | 0.42 |
| 3.10-helix | - | - | - | - | - | 0.09 | - |
| α-helix | 0.08 | 0.02 | 0.05 | 0.05 | 0.05 | <0.20 | ~0.01 |
| α-helix + β-sheet | - | - | - | - | - | 0.51 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lukasheva, N.; Tolmachev, D.; Martinez-Seara, H.; Karttunen, M. Changes in the Local Conformational States Caused by Simple Na+ and K+ Ions in Polyelectrolyte Simulations: Comparison of Seven Force Fields with and without NBFIX and ECC Corrections. Polymers 2022, 14, 252. https://doi.org/10.3390/polym14020252
Lukasheva N, Tolmachev D, Martinez-Seara H, Karttunen M. Changes in the Local Conformational States Caused by Simple Na+ and K+ Ions in Polyelectrolyte Simulations: Comparison of Seven Force Fields with and without NBFIX and ECC Corrections. Polymers. 2022; 14(2):252. https://doi.org/10.3390/polym14020252
Chicago/Turabian StyleLukasheva, Natalia, Dmitry Tolmachev, Hector Martinez-Seara, and Mikko Karttunen. 2022. "Changes in the Local Conformational States Caused by Simple Na+ and K+ Ions in Polyelectrolyte Simulations: Comparison of Seven Force Fields with and without NBFIX and ECC Corrections" Polymers 14, no. 2: 252. https://doi.org/10.3390/polym14020252
APA StyleLukasheva, N., Tolmachev, D., Martinez-Seara, H., & Karttunen, M. (2022). Changes in the Local Conformational States Caused by Simple Na+ and K+ Ions in Polyelectrolyte Simulations: Comparison of Seven Force Fields with and without NBFIX and ECC Corrections. Polymers, 14(2), 252. https://doi.org/10.3390/polym14020252