The Effectiveness of CFRP- and Auxetic Fabric-Strengthened Brick Masonry under Axial Compression: A Numerical Investigation
Abstract
:1. Introduction
2. Numerical Modelling of URM Axial Compression
2.1. Experimental Programme
2.2. Model Geometry Details
2.3. Material Properties and Constitutive Model
2.4. Zero Thickness Interface: Cohesive Zone Model
2.5. Validation Results
2.5.1. Failure Modes
2.5.2. Monotonic and Cyclic Stress-Strain Relationship
3. Numerical Modelling of Strengthened Brick Wallettes under Axial Compression
3.1. CFRP Fabric: Geometric Detailing
3.2. CFRP Fabric: Material Properties
3.3. CFRP Fabric Brick Wallettes: Interface Modelling
3.4. Validation of the CFRP Fabric-Strengthened Brick Wallettes under Monotonic Compression Loading
3.5. Prediction of Cyclic Behaviour of CFRP Fabric-Strengthened Brickwork Wallettes
4. Alternative Strengthening of Masonry Using Auxetic Fabrics
4.1. Auxetic Fabric-Strengthened Masonry Wallettes under Compression Loading
4.2. Auxetic Fabric-Strengthened Masonry Wallettes under Cyclic Compression
5. Summary and Conclusions
- ▪
- The simplified micro-modelling technique for the masonry wallettes constructed with different brick types was found to be computationally efficient without compromising the accuracy in predicting compression behaviour under the monotonic and cyclic compression loading protocols.
- ▪
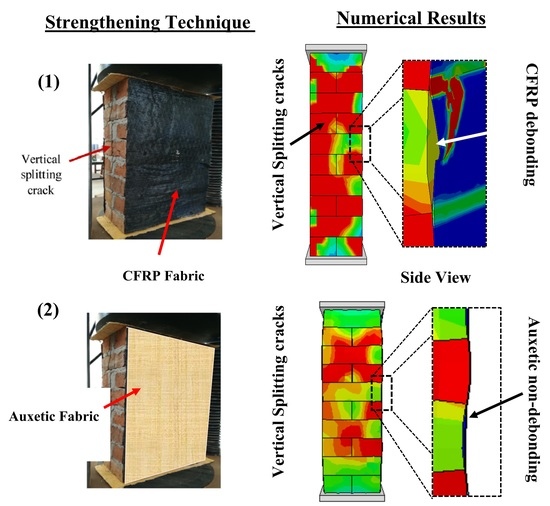
- Due to the de-bonding nature of failure in CFRP-strengthened masonry wallettes, the increases in the compressive resistance and ductility of masonry wallettes were limited. This phenomenon was more pronounced in the cyclic loading conditions, where with progressive damage, premature compression failures were observed due to early de-bonding.
- ▪
- The CFRP strengthening increased the compressive resistance of the masonry wallettes compared to the un-strengthened masonry wallettes by about 10–20%. In contrast, the auxetic fabric application increased the compressive resistance of brickwork by 38–60% under monotonic loading.
- ▪
- In cyclic compression loading, the auxetic fabric application to the surface of the masonry wallettes increased the ultimate strains without compromising the strength, compared to the un-strengthened masonry wallettes, which significantly enhanced the ductility (up to ~50%) of the masonry wallettes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mazumdar, S. Composites Manufacturing: Materials, Product, and Process Engineering; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Olivito, R.; Cevallos, O.; Carrozzini, A. Development of durable cementitious composites using sisal and flax fabrics for reinforcement of masonry structures. Mater. Design 2014, 57, 258–268. [Google Scholar] [CrossRef]
- Pichandi, S.; Rana, S.; Oliveira, D.; Fangueiro, R. Fibrous and composite materials for blast protection of structural elements—A state-of-the-art review. J. Reinf. Plast. Compos. 2013, 32, 1477–1500. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C. Combined effects of sustained bending loading, water immersion and fiber hybrid mode on the mechanical properties of carbon/glass fiber reinforced polymer composite. Compos. Struct. 2022, 281, 115060. [Google Scholar] [CrossRef]
- Li, C.; Xian, G.; Li, H. Influence of immersion in water under hydraulic pressure on the interfacial shear strength of a unidirectional carbon/glass hybrid rod. Polym. Test. 2018, 72, 164–171. [Google Scholar] [CrossRef]
- Li, C.; Xian, G.; Li, H. Water Absorption and Distribution in a Pultruded Unidirectional Carbon/Glass Hybrid Rod under Hydraulic Pressure and Elevated Temperatures. Polymers 2018, 10, 627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, R.; Xian, G.; Li, F.; Li, C.; Hong, B. Hygrothermal resistance of pultruded carbon, glass and carbon/glass hybrid fiber reinforced epoxy composites. Constr. Build. Mater. 2022, 315, 125710. [Google Scholar] [CrossRef]
- Altin, S.; Ani, Ö.; Kara, M.E.; Kaya, M. An experimental study on strengthening of masonry infilled RC frames using diagonal CFRP strips. Compos. B Eng. 2008, 39, 680–693. [Google Scholar] [CrossRef]
- Dizhur, D.; Griffith, M.; Ingham, J. In-plane shear improvement of unreinforced masonry wall panels using NSM CFRP strips. J. Compos. Construct. 2013, 17, 04013010. [Google Scholar] [CrossRef]
- Marcari, G.; Manfredi, G.; Prota, A.; Pecce, M. In-plane shear performance of masonry panels strengthened with FRP. Compos. Part B Eng. 2007, 38, 887–901. [Google Scholar] [CrossRef]
- Konthesingha, K.M.C.; Masia, M.J.; Petersen, R.B.; Mojsilovic, N.; Simundic, G.; Page, A.W. Static cyclic in-plane shear response of damaged masonry walls retrofitted with NSM FRP strips—An experimental evaluation. Eng. Struct. 2013, 50, 126–136. [Google Scholar] [CrossRef]
- Grande, E.; Fagone, M.; Rotunno, T.; Bertolesi, E.; Milani, G. Modelling of the bond behaviour of curved masonry specimens strengthened by CFRP with anchor spikes. Compos. B Eng. 2019, 174, 235–245. [Google Scholar] [CrossRef]
- Corradi, M.; Castori, G.; Sisti, R.; Borri, A.; Pesce, G.L. Repair of Block Masonry Panels with CFRP Sheets. Materials 2019, 12, 2363. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jafari, A.; Oskouei, A.V.; Bazli, M.; Ghahri, R. Effect of the FRP sheet’s arrays and NSM FRP bars on in-plane behavior of URM walls. J. Build. Eng. 2018, 20, 679–695. [Google Scholar] [CrossRef]
- Siddika, A.; al Mamun, M.A.; Alyousef, R.; Amran, Y.M. Strengthening of reinforced concrete beams by using fiber-reinforced polymer composites: A review. J. Build. Eng. 2019, 25, 100798. [Google Scholar] [CrossRef]
- Thamboo, J.A.; Dhanasekar, M. Assessment of the characteristics of lime mortar bonded brickwork wallettes under monotonic and cyclic compression. Constr. Build. Mater. 2020, 261, 120003. [Google Scholar] [CrossRef]
- Thamboo, J.; Navaratnam, S.; Poologanathan, K.; Corradi, M. Characteristics of CFRP strengthened masonry wallettes under concentric and eccentric compression. Case Studies Const. Mater. 2020, 14, e00472. [Google Scholar] [CrossRef]
- Li, C.; Xian, G. Novel wedge-shaped bond anchorage system for pultruded CFRP plates. Mater. Struct. 2018, 51, 162. [Google Scholar] [CrossRef]
- Ghafoori, E.; Motavalli, M.; Nussbaumer, A.; Herwig, A.; Prinz, G.; Fontana, M. Determination of minimum CFRP pre-stress levels for fatigue crack prevention in retrofitted metallic beams. Eng. Struct. 2015, 84, 29–41. [Google Scholar] [CrossRef]
- Mahmood, H.; Ingham, J.M. Diagonal compression testing of FRP-retrofitted unreinforced clay brick masonry wallettes. J. Compos. Constr. 2011, 15, 810–820. [Google Scholar] [CrossRef] [Green Version]
- Bertolesi, E.; Milani, G.; Carozzi, F.G.; Poggi, C. Ancient masonry arches and vaults strengthened with TRM, SRG and FRP composites: Numerical analyses. Compos. Struct. 2018, 187, 385–402. [Google Scholar] [CrossRef]
- Carozzi, F.G.; Poggi, C.; Bertolesi, E.; Milani, G. Ancient masonry arches and vaults strengthened with TRM, SRG and FRP composites: Experimental evaluation. Compos. Struct. 2018, 187, 466–480. [Google Scholar] [CrossRef] [Green Version]
- Papanicolaou, C.G.; Triantafillou, T.C.; Papathanasiou, M.; Karlos, K. Textile reinforced mortar (TRM) versus FRP as strengthening material of URM walls: Out-of-plane cyclic loading. Mater. Struct. 2008, 41, 143–157. [Google Scholar] [CrossRef]
- Bertolesi, E.; Buitrago, M.; Giordano, E.; Calderon, P.A.; Moragues, J.J.; Clementi, F.; Adam, J.M. Effectiveness of textile reinforced mortar (TRM) materials in preventing seismic-induced damage in a U-shaped masonry structure submitted to pseudodynamic excitations. Construct. Build. Mater. 2020, 248, 118532. [Google Scholar] [CrossRef]
- Lignola, G.P.; Caggegi, C.; Ceroni, F.; de Santis, S.; Krajewski, P.; Lourenço, P.B.; Morganti, M.; Papanicolaou, C.C.; Pellegrino, C.; Prota, A.; et al. Performance assessment of basalt FRCM for retrofit applications on masonry. Compos. Part B Eng. 2017, 128, 1–18. [Google Scholar] [CrossRef]
- Ghiassi, B.; Oliveira, D.V.; Marques, V.; Soares, E.; Maljaee, H. Multi-level characterization of steel reinforced mortars for strengthening of masonry structures. Mater. Des. 2016, 110, 903–913. [Google Scholar] [CrossRef]
- Bellini, A.; Shahreza, S.K.; Mazzotti, C. Cyclic bond behavior of FRCM composites applied on masonry substrate. Compos. Part B Eng. 2019, 169, 189–199. [Google Scholar] [CrossRef]
- de Santis, S.; Roscini, F.; de Felice, G. Full-scale tests on masonry vaults strengthened with Steel Reinforced Grout. Composites Part B 2018, 141, 20–36. [Google Scholar] [CrossRef]
- Thamboo, J.; Zahra, T.; Asad, M. Monotonic and cyclic compression characteristics of CFRP confined masonry columns. Compos. Struct. 2021, 272, 114257. [Google Scholar] [CrossRef]
- Kamrava, A.R.; Najafgholipour, M.A.; Fathi, F.; Dehghan, S.M. An experimental study on the in-plane behavior of unreinforced masonry walls with an opening strengthened using steel fiber reinforced concrete overlays. J. Build. Eng. 2021, 36, 102084. [Google Scholar] [CrossRef]
- Triantafillou, T.C. Strengthening of masonry structures using epoxy-bonded FRP laminates. J. Compos. Constr. 1998, 2, 96–104. [Google Scholar] [CrossRef]
- Cheng, L.; McComb, A.M. Unreinforced concrete masonry walls strengthened with CFRP sheets and strips under pendulum impact. J. Compos. Constr. 2010, 14, 775–783. [Google Scholar] [CrossRef]
- Schmidt, M.E.; Cheng, L. Impact response of externally strengthened unreinforced masonry walls using CFRP. J. Compos. Constr. 2009, 13, 252–261. [Google Scholar] [CrossRef]
- Kiruthika, A.V. A review on physico-mechanical properties of bast fibre reinforced polymer composites. J. Build. Eng. 2017, 9, 91–99. [Google Scholar] [CrossRef]
- Kadhim, M.M.A.; Jawdhari, A.R.; Altaee, M.J.; Adheem, A.H. Finite element modelling and parametric analysis of FRP strengthened RC beams under impact load. J. Build. Eng. 2020, 32, 101526. [Google Scholar] [CrossRef]
- Asad, M.; Zahra, T.; Thambiratnam, D.P.; Chan, T.H.T.; Zhuge, Y. Geometrically modified auxetic polyurethane foams and their potential application in impact mitigation of masonry structures. Constr. Build. Mater. 2021, 311, 125170. [Google Scholar] [CrossRef]
- Asad, M.; Dhanasekar, M.; Zahra, T.; Thambiratnam, D. Characterisation of polymer cement mortar composites containing carbon fibre or auxetic fabric overlays and inserts under flexure. Construct. Build. Mater. 2019, 224, 863–879. [Google Scholar] [CrossRef]
- Asad, M.; Dhanasekar, M.; Zahra, T.; Thambiratnam, D. Impact mitigation of masonry walls with carbon fibre and Auxetic fibre composite renders—A numerical study. Structures 2020, 28, 2733–2751. [Google Scholar] [CrossRef]
- Murray, G.J.; Gandhi, F. Auxetic honeycombs with lossy polymeric infills for high damping structural materials. J. Intell. Mater. Syst. Struct. 2013, 24, 1090–1104. [Google Scholar] [CrossRef]
- PKoutsianitis, I.; Tairidis, G.K.; Drosopoulos, G.A.; Stavroulakis, G.E. Conventional and star-shaped auxetic materials for the creation of band gaps. Arch. Appl. Mech. 2019, 89, 2545–2562. [Google Scholar] [CrossRef]
- d’Alessandro, L.; Zega, V.; Ardito, R.; Corigliano, A. 3D auxetic single material periodic structure with ultra-wide tunable bandgap. Sci. Rep. 2018, 8, 2262. [Google Scholar] [CrossRef] [Green Version]
- Naidoo, P.; Drosopoulos, G. Evaluation of the dynamic response of structures using auxetic-type base isolation. Frat. Integrità Strutt. 2020, 51, 52–70. [Google Scholar]
- Lowe, A.; Lakes, R. Negative Poisson’s ratio foam as seat cushion material. Cell Polym. 2000, 19, 157–168. [Google Scholar]
- Rana, S.; Fangueiro, R. Advanced composites in aerospace engineering. In Advanced Composite Materials for Aerospace Engineering; Elsevier: Amsterdam, The Netherlands, 2016; pp. 1–15. [Google Scholar]
- Caddock, B.D.; Evans, K.E. Negative Poisson ratios and strain-dependent mechanical properties in arterial prostheses. Biomaterials 1995, 16, 1109–1115. [Google Scholar] [CrossRef]
- Bhulla, S.K.; Ko, J.; Ahmed, F.; Jun, M.B.G. Design and fabrication of stent with negative Poisson’s ratio. World Academy of Science, Engineering and Technology. Int. J. Mech. Mechatron. Eng. 2014, 8, 448–454. [Google Scholar]
- Ali, M.N.; Busfield, J.J.; Rehman, I.U. Auxetic oesophageal stents: Structure and mechanical properties. J. Mater. Sci. Mater. Med. 2014, 25, 527–553. [Google Scholar] [CrossRef]
- Miller, W.; Ren, Z.; Smith, C.; Evans, K. A negative Poisson’s ratio carbon fibre composite using a negative Poisson’s ratio yarn reinforcement. Compos. Sci. Technol. 2021, 72, 761–766. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L. Auxetic materials. P I Mech. Eng. G-J. Aer. 2007, 221, 565–575. [Google Scholar] [CrossRef]
- Argatov, I.I.; Guinovart-Díaz, R.; Sabina, F.J. On local indentation and impact compliance of isotropic auxetic materials from the continuum mechanics viewpoint. Int. J. Eng. Sci. 2012, 54, 42–57. [Google Scholar] [CrossRef]
- Hamed, A.A.; Asl, R.B.; Rahimzadeh, H. Experimental and numerical study on the structural performance of auxetic-shaped, ring-shaped and unstiffened steel plate shear walls. J. Build. Eng. 2021, 34, 101939. [Google Scholar] [CrossRef]
- Zahra, T.; Dhanasekar, M. Characterisation and strategies for mitigation of the contact surface unevenness in dry-stack masonry. Constr. Build. Mater. 2018, 169, 612–628. [Google Scholar] [CrossRef]
- Zahra, T.; Dhanasekar, M. Characterisation of cementitious polymer mortar—Auxetic foam composites. Constr. Build. Mater. 2017, 147, 143–159. [Google Scholar] [CrossRef] [Green Version]
- Asad, M.; Dhanasekar, M.; Zahra, T.; Thambiratnam, D. Mitigating impact failure of masonry boundary walls using auxetic composites. In Proceedings of the 10th Australasian Masonry Conference, Sydney, NSW, Australia, 11–14 February 2018; pp. 523–534. [Google Scholar]
- Lourenço, B.P.; Rots, J.G. Multisurface interface model for analysis of masonry structures. J. Eng. Mech. 1997, 123, 660–668. [Google Scholar] [CrossRef]
- Milani, G.; Lourenço, P.; Tralli, A. Homogenization approach for the limit analysis of out-of-plane loaded masonry walls. J. Struct. Eng. 2006, 132, 1650–1663. [Google Scholar] [CrossRef]
- Bui, T.-L.; Djamai, Z.I.; Larbi, A.S.; Reboul, N.; Ferrier, E. Numerical study of composite material (FRP/TRC)-reinforced masonry walls under in-plane loading. J. Compos. Mater. 2021, 55, 3425–3441. [Google Scholar] [CrossRef]
- Grande, E.; Milani, G.; Sacco, E. Modelling and analysis of FRP-strengthened masonry panels. Eng. Struct. 2008, 30, 1842–1860. [Google Scholar] [CrossRef]
- Mirkhalaf, M.; Barthelat, F. Nacre-like materials using a simple doctor blading technique: Fabrication, testing and modeling. J. Mech. Behav. Biomed. Mater. 2016, 56, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Abid, N.; Mirkhalaf, M.; Barthelat, F. Discrete-element modeling of nacre-like materials: Effects of random microstructures on strain localization and mechanical performance. J. Mech. Phys. Solids 2018, 112, 385–402. [Google Scholar] [CrossRef]
- Barthelat, F. Designing nacre-like materials for simultaneous stiffness, strength and toughness: Optimum materials, composition, microstructure and size. J. Mech. Phys. Solids 2014, 73, 22–37. [Google Scholar] [CrossRef]
- Barthelat, F.; Tang, H.; Zavattieri, P.; Li, C.-M.; Espinosa, H. On the mechanics of mother-of-pearl: A key feature in the material hierarchical structure. J. Mech. Phys. Solids 2007, 55, 306–337. [Google Scholar] [CrossRef]
- Bahmani, A.; Li, G.; Willett, T.L.; Montesano, J. Three-dimensional micromechanical assessment of bio-inspired composites with non-uniformly dispersed inclusions. Compos. Struct. 2019, 212, 484–499. [Google Scholar] [CrossRef]
- Zahra, T.; Asad, M.; Thamboo, J. Effect of geometry on the compression characteristics of bonded brickwork. Structures 2021, 32, 1408–1419. [Google Scholar] [CrossRef]
- BS EN 1052-1:1999; Methods of Test for Masonry. Determination of Compressive Strength. BSI: London, UK, 1999.
- ABAQUS, Abaqus 6.19 Documentation; SIMULIA: Johnston, RI, USA, 2019.
- Asad, M.; Dhanasekar, M.; Zahra, T.; Thambiratnam, D. Failure analysis of masonry walls subjected to low velocity impacts. Eng. Fail. Anal. 2020, 116, 104706. [Google Scholar] [CrossRef]
- Asad, M.; Zahra, T.; Thambiratnam, D. Failure of Masonry Walls under High Velocity Impact—A Numerical Study. Eng Struc. 2021, 238, 112009. [Google Scholar] [CrossRef]
- Jankowiak, T.; Lodygowski, T. Identification of parameters of concrete damage plasticity constitutive model. Found. Civ. Environ. Eng. 2005, 6, 53–69. [Google Scholar]
- Zahra, T.; Thamboo, J.; Asad, M. Compressive strength and deformation characteristics of concrete block masonry made with different mortars, blocks and mortar beddings types. J. Build. Eng. 2021, 38, 102213. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed mode bending apparatus. Compos. Sci. Technol. 1996, 49, 439–449. [Google Scholar] [CrossRef]
- Costigan, A.; Pavía, S.; Kinnane, O. An experimental evaluation of prediction models for the mechanical behavior of unreinforced, lime-mortar masonry under compression. J. Build. Eng. 2015, 4, 283–294. [Google Scholar] [CrossRef] [Green Version]
- Thamboo, J.; Bandara, J.; Perera, S.; Navaratnam, S.; Poologanathan, K.; Corradi, M. Experimental and analytical study of masonry subjected to uniaxial cyclic compression. Materials 2020, 13, 4505. [Google Scholar] [CrossRef]
- Thamboo, J.A.; Dhanasekar, M. Correlation between the performance of solid masonry prisms and wallettes under compression. J. Build. Eng. 2019, 22, 429–438. [Google Scholar] [CrossRef]
- Noor-E-Khuda, S.; Dhanasekar, M.; Thambiratnam, D. An explicit finite element modelling method for masonry walls under out-of-plane loading. Eng Struct. 2016, 113, 103–120. [Google Scholar] [CrossRef] [Green Version]
- Asad, M. Failure Analysis and Mitigating Strategies for Masonry Walls Subject to Vehicular Impacts. PhD Thesis, Queensland University of Technology, Brisbane, QLD, Australia, 2020. [Google Scholar]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Imran, M.; Mahendran, M.; Keerthan, P. Experimental and numerical investigations of CFRP strengthened short SHS steel columns. Eng. Struct. 2018, 175, 879–894. [Google Scholar] [CrossRef]
- Tafsirojjaman, T.; Fawzia, S.; Thambiratnam, D.P.; Zhao, X.L. Study on the cyclic bending behaviour of CFRP strengthened full-scale CHS members. Structures 2020, 28, 741–756. [Google Scholar] [CrossRef]
- Witzany, J.; Zigler, R.; Kroftová, K. Strengthening of compressed brick masonry walls with carbon composites. Constr. Build. Mater. 2016, 112, 1066–1079. [Google Scholar] [CrossRef]
- Witzany, J.; Cejka, T.; Zigler, R. Strengthening of historical masonry vaults and pillars with carbon fabric. In Smart Monitoring, Assessment and Rehabilitation in Civil Structures; American University in Dubai UAE: Dubai, United Arab Emirates, 2011; p. 122. ISBN 978-3-905594-58-4. [Google Scholar]























| Wallettes | Wallette Dimension (mm) (L × W × H) | Type of Test | Number of Wallettes Tested | Compressive Strength MPa (CoV) |
|---|---|---|---|---|
| B1 Brick | 410 × 200 × 740 | Monotonic Cyclic | 4 3 | 2.28 (9.3) 1.93 (12.7) |
| B2 Brick | 410 × 200 × 740 | Monotonic Cyclic | 4 3 | 6.66 (5.4) 5.46 (6.5) |
| Monotonic Loading | Cyclic Loading | |
|---|---|---|
| Load-Displacement Response | Number of Steps | Number of Cycles |
| Elastic Limit (one-third of peak load) | 4 steps | 2 cycles at each step |
| Hardening Limit (0.8 times the peak load) | 4 Steps | 2 cycles at each step |
| Peak Limit | 3 Steps | 2 cycles at each step |
| Parameter | Magnitude |
|---|---|
| Dilation angle (ψ) | 300 |
| Eccentricity (e) | 0.1 |
| Strength ratio (fb0/fc0) | 1.16 |
| Shape factor (Kc) | 0.66 |
| Viscosity (µ) | 0.001 |
| Parameter | Magnitude |
|---|---|
| Normal stiffness, (N/mm3) | 28 |
| Shear stiffness, (N/mm3) | 32 |
| Friction coefficient | 0.6 |
| Maximum tensile stress, (MPa) | 0.68 |
| Maximum shear stress, and (MPa) | 0.82 |
| Young’s Modulus (x-Axis) E1 (MPa) | Young’s Modulus (y-Axis) E2 (MPa) | Poisson’s Ratio in (xy Plane) | Shear Modulus (xy Plane) G12 (MPa) | Shear Modulus (xz Plane) G13 (MPa) | Shear Modulus (yz Plane) G23 (MPa) | Density (kg/m3) |
|---|---|---|---|---|---|---|
| 88,600 | 22,200 | 0.33 | 7067 | 3000 | 3000 | 1820 |
| Fibre Tensile Strength (MPa) | Tensile Strength (y-Axis) (MPa) | Longitudinal Shear Strength (MPa) | Transverse Shear Strength (MPa) |
|---|---|---|---|
| 903 | 150 | 40 | 10 |
| Fibre Tensile Fracture Energy (mJ/mm2) | Matrix Tensile Energy (mJ/mm2) |
|---|---|
| 91.6 | 0.22 |
| Parameter | Value |
|---|---|
| Elastic modulus of adhesive, Ea | 1.995 GPa |
| Maximum tensile stress, | 49.3 MPa |
| Maximum shear stress, | 44.4 MPa |
| Normal stiffness, | 1.995 × 103 N/m3 |
| Shear stiffness, | 1 × 103 N/m3 |
| Maximum fracture energies in normal, | 3900 N/m |
| Maximum fracture energies in shear, | 110,000 N/m |
| Young’s Modulus (x-Axis)/E1 (MPa) | Young’s Modulus (y-axis) E2 (MPa) | Poisson’s Ratio in (xy Plane) | Shear Modulus (xy Plane) G12 (MPa) | Shear Modulus (xz Plane) G13 (MPa) | Shear Modulus (yz Plane) G23 (MPa) | Density (kg/m3) |
|---|---|---|---|---|---|---|
| 400 | 181.2 | −0.9 | 194.5 | 194.5 | 103.4 | 450 |
| Fibre Tensile Strength (MPa) | Tensile Strength (y-Axis) (MPa) | Longitudinal Shear Strength (MPa) | Transverse Shear Strength (MPa) |
|---|---|---|---|
| 50.0 | 40.4 | 10.1 | 10.1 |
| Fibre Tensile Fracture Energy | Matrix Tensile Energy |
|---|---|
| 130.3 | 130.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Asad, M.; Zahra, T.; Thamboo, J. The Effectiveness of CFRP- and Auxetic Fabric-Strengthened Brick Masonry under Axial Compression: A Numerical Investigation. Polymers 2022, 14, 1800. https://doi.org/10.3390/polym14091800
Asad M, Zahra T, Thamboo J. The Effectiveness of CFRP- and Auxetic Fabric-Strengthened Brick Masonry under Axial Compression: A Numerical Investigation. Polymers. 2022; 14(9):1800. https://doi.org/10.3390/polym14091800
Chicago/Turabian StyleAsad, Mohammad, Tatheer Zahra, and Julian Thamboo. 2022. "The Effectiveness of CFRP- and Auxetic Fabric-Strengthened Brick Masonry under Axial Compression: A Numerical Investigation" Polymers 14, no. 9: 1800. https://doi.org/10.3390/polym14091800
APA StyleAsad, M., Zahra, T., & Thamboo, J. (2022). The Effectiveness of CFRP- and Auxetic Fabric-Strengthened Brick Masonry under Axial Compression: A Numerical Investigation. Polymers, 14(9), 1800. https://doi.org/10.3390/polym14091800