Effect of Cyclic Shear Fatigue under Magnetic Field on Natural Rubber Composite as Anisotropic Magnetorheological Elastomers
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
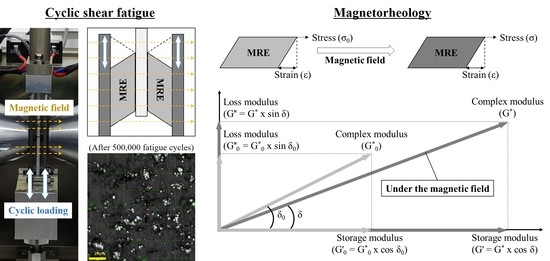
3.1. Cyclic Shear Fatigue Test
3.2. Morphology
3.3. Specific Gravity
3.4. Rheological Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hosseini, S.M.; Shojaeefard, M.H.; Saeidi, G.H. Fatigue life prediction of magneto-rheological elastomers in magnetic field. Mater. Res. Express. 2021, 8, 025304. [Google Scholar] [CrossRef]
- Laraba-Abbes, F.; Ienny, P.; Piques, R. A new ‘Tailor-made’ methodology for the mechanical behaviour analysis of rubber-like materials: II. Application to the hyperelastic behaviour characterization of a carbon-black filled natural rubber vulcanizate. Polymer 2003, 44, 821–840. [Google Scholar]
- Wang, X.L.; Liao, M.Y.; Xu, Y.; Liu, X.A. Fatigue crack propagation characteristics of rubbery materials under variable amplitude loading. Results Phys. 2018, 10, 233–240. [Google Scholar] [CrossRef]
- Tee, Y.L.; Loo, M.S.; Andriyana, A. Recent advances on fatigue of rubber after the literature survey by Mars and Fatemi in 2002 and 2004. Int. J. Fatigue 2018, 110, 115–129. [Google Scholar] [CrossRef]
- Shangguan, W.B.; Wang, X.L.; Deng, J.X.; Rakheja, S.; Pan, X.Y.; Yu, B. Experiment and modeling of uniaxial tension fatigue performances for filled natural rubbers. Mater. Des. 2014, 58, 65–73. [Google Scholar] [CrossRef]
- Gent, A.N.; Lindley, P.B.; Thomas, A.G. Cut growth and fatigue of rubbers. I. The relationship between cut growth and fatigue. J. Appl. Polym. Sci. 1964, 8, 455–466. [Google Scholar]
- Yeoh, O.H. Analysis of deformation and fracture of ‘pure shear’ rubber testpiece. Plast. Rubber. Compos. 2001, 30, 389–397. [Google Scholar] [CrossRef]
- Luo, W.; Huang, Y.; Yin, B.; Jiang, X.; Hu, X. Fatigue life assessment of filled rubber by hysteresis induced self-heating temperature. Polymers 2020, 12, 846. [Google Scholar] [CrossRef] [Green Version]
- Le, S.V.; Marco, Y.; Calloch, S.; Doudard, C.; Charrier, P. Fast evaluation of the fatigue lifetime of rubber-like materials based on a heat build-up protocol and micro-tomography measurements. Int. J. Fatigue 2010, 32, 1582–1590. [Google Scholar]
- Luo, W.; Yin, B.; Hu, X.; Zhou, Z.; Deng, Y.; Song, K. Modeling of the heat build-up of carbon black filled rubber. Polym. Test. 2018, 69, 116–124. [Google Scholar] [CrossRef]
- Zhi, J.; Wang, S.; Zhang, M.; Wang, H.; Lu, H.; Lin, W. Numerical analysis of the dependence of rubber hysteresis loss and heat generation on temperature and frequency. Mech. Time-Depend. Mat. 2019, 23, 427–442. [Google Scholar] [CrossRef]
- Le, S.V.; Marco, Y.; Calloch, S.; Charrier, P.; Taveau, D. Heat build-up of rubber under cyclic loadings: Validation of an efficient demarch to predict the temperature fields. Rubber Chem. Technol. 2013, 86, 38–56. [Google Scholar]
- Katunin, A. Criticality of the self-heating effect in polymers and polymer matrix composites during fatigue, and their application in non-destructive testing. Polymers 2019, 11, 19. [Google Scholar] [CrossRef] [Green Version]
- Schümann, M.; Odenbach, S. In-situ observation of the particle microstructure of magnetorheological elastomers in presence of mechanical strain and magnetic fields. J. Magn. Magn. Mater. 2017, 441, 88–92. [Google Scholar] [CrossRef]
- Perales-Martínez, I.A.; Palacios-Pineda, L.M.; Lozano-Sánchez, L.M.; Martínez-Romero, O.; Puente-Cordova, J.G.; Elías-Zúñiga, A. Enhancement of a magnetorheological PDMS elastomer with carbonyl iron particles. Polym. Test. 2017, 57, 78–86. [Google Scholar] [CrossRef]
- Burgaz, E.; Goksuzoglu, M. Effects of magnetic particles and carbon black on structure and properties of magnetorheological elastomers. Polym. Test. 2020, 81, 106233. [Google Scholar] [CrossRef]
- Cvek, M.; Kracalik, M.; Sedlacik, M.; Mrlik, M.; Sedlarik, V. Reprocessing of injection-molded magnetorheological elastomers based on TPE matrix. Compos. B. Eng. 2019, 172, 253–261. [Google Scholar] [CrossRef]
- Yu, M.; Qi, S.; Fu, J.; Zhu, M.; Chen, D. Understanding the reinforcing behaviors of polyaniline-modified carbonyl iron particles in magnetorheological elastomer based on polyurethane/epoxy resin IPNs matrix. Compos. Sci. Technol. 2017, 139, 36–46. [Google Scholar] [CrossRef]
- Dargahi, A.; Sedaghati, R.; Rakheja, S. On the properties of magnetorheological elastomers in shear mode: Design, fabrication and characterization. Compos. B. Eng. 2019, 159, 269–283. [Google Scholar] [CrossRef]
- Na, B.G.; Chung, K.H. Effect of precured EPDM on the property of magneto-rheological elastomer based on NR/EPDM blend. Elast. Compos. 2018, 53, 67–74. [Google Scholar]
- Kim, T.W.; Choi, Y.J.; Kim, N.Y.; Chung, K.H. A study on the fatigue property of magneto-rheological elastomers. Elast. Compos. 2018, 53, 150–157. [Google Scholar]
- Zhou, Y.; Johnson, M.; Wen, S.; Betts, A.; Jerrams, S. Equi-biaxial fatigue behaviour of magnetorheological elastomers in magnetic fields. J. Intell. Mater. Syst. Struct. 2016, 28, 687–696. [Google Scholar] [CrossRef]
- Lian, C.; Lee, K.H.; Choi, S.B.; Lee, C.H. A study of the magnetic fatigue properties of a magnetorheological elastomer. J. Intell. Mater. Syst. Struct. 2018, 30, 749–754. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, X.; Yang, J.; Xuan, S. Improving the dynamic properties of MRE under cyclic loading by incorporating silicon carbide nanoparticles. Ind. Eng. Chem. Res. 2014, 53, 3065–3072. [Google Scholar] [CrossRef] [Green Version]
- Gorman, D.; Murphy, N.; Ekins, R.; Jerrams, S. The evaluation and implementation of magnetic fields for large strain uniaxial and biaxial cyclic testing of magnetorheological elastomers. Polym. Test. 2016, 51, 74–81. [Google Scholar] [CrossRef] [Green Version]
- Johari, M.A.F.; Mazlan, S.A.; Nasef, M.M.; Ubaidillah, U.; Nordin, N.A.; Aziz, S.A.A.; Johari, N.; Nazmi, N. Microstructural behavior of magnetorheological elastomer undergoing durability evaluation by stress relaxation. Sci. Rep. 2021, 11, 10936. [Google Scholar] [CrossRef]
- Yoon, J.H.; Lee, S.W.; Bae, S.H.; Kim, N.I.; Yun, J.H.; Ryu, S.H. Effect of alignment of magnetic particles on the rheological properties of natural rubber composite. J. Polym. Res. 2021, 28, 367. [Google Scholar] [CrossRef]
- Ubaidillah; Sutrisno, J.; Purwanto, A.; Mazlan, S.A. Recent progress on magnetorheological solids: Materials, fabrication, testing, and applications. Adv. Eng. Mater. 2015, 17, 563–597. [Google Scholar] [CrossRef]
- Bodelot, L.; Voropaieff, J.P.; Pössinger, T. Experimental investigation of the coupled magneto-mechanical response in magnetorheological elastomers. Exp. Mech. 2018, 58, 207–221. [Google Scholar] [CrossRef] [Green Version]
- Syam, T.; Muthalif, A.; Salem, A.; Hejazi, A. 3D numerical modelling and analysis of a magnetorheological elastomer (MRE). J. Vibroengineering 2020, 22, 1251–1265. [Google Scholar]
- Cantournet, S.; Desmorat, R.; Besson, J. Mullins effect and cyclic stress softening of filled elastomers by internal sliding and friction thermodynamics model. Int. J. Solids Struct. 2009, 46, 2255–2264. [Google Scholar] [CrossRef]
- Harwood, J.A.C.; Payne, A.R. Stress softening in natural rubber vulcanizates. Part III. Carbon black-filled vulcanizates. J. Appl. Polym. Sci. 1966, 10, 315–324. [Google Scholar]
- Harwood, J.A.C.; Payne, A.R. Hysteresis and strength of rubbers. J. Appl. Polym. Sci. 1968, 12, 889–901. [Google Scholar] [CrossRef]
- Mullins, L.; Tobin, N.R. Theoretical model for the elastic behavior of filler-reinforced vulcanized rubbers. Rubber Chem. Technol. 1957, 30, 555–571. [Google Scholar] [CrossRef]
- Mullins, L.; Tobin, N.R. Stress softening in rubber vulcanizates. Part I. Use of a strain amplification factor to describe the elastic behavior of filler-reinforced vulcanized rubber. J. Appl. Polym. Sci. 1965, 9, 2993–3009. [Google Scholar] [CrossRef]
- Qi, H.J.; Boyce, M.C. Constitutive model for stretch-induced softening of the stress–stretch behavior of elastomeric materials. J. Mech. Phys. Solids 2004, 52, 2187–2205. [Google Scholar] [CrossRef]
- Saintier, N.; Cailletaud, G.; Piques, R. Cyclic loadings and crystallization of natural rubber: An explanation of fatigue crack propagation reinforcement under a positive loading ratio. Mater. Sci. Eng. A 2011, 528, 1078–1086. [Google Scholar] [CrossRef]
- Yu, M.; Fu, J.; Ju, B.X.; Zheng, X.; Choi, S.B. Influence of x-ray radiation on the properties of magnetorheological elastomers. Smart. Mater. Struct. 2013, 22, 125010. [Google Scholar] [CrossRef]
- Fan, Y.; Gong, X.; Xuan, S.; Qin, L.; Li, X. Effect of cross-link density of the matrix on the damping properties of magnetorheological elastomers. Ind. Eng. Chem. Res. 2013, 52, 771–778. [Google Scholar] [CrossRef]
- Yang, J.; Gong, X.; Deng, H.; Qin, L.; Xuan, S. Investigation on the mechanism of damping behavior of magnetorheological elastomers. Smart. Mater. Struct. 2012, 21, 125015. [Google Scholar] [CrossRef]
- Movahedi-Rad, A.V.; Keller, T.; Vassilopoulos, A.P. Modeling of fatigue behavior based on interaction between time- and cyclic-dependent mechanical properties. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105469. [Google Scholar] [CrossRef]
- Movahedi-Rad, A.; Keller, T.; Vassilopoulos, A. Interrupted tension-tension fatigue behavior of angle-ply GFRP composite laminates. Int. J. Fatigue 2018, 113, 377–388. [Google Scholar] [CrossRef]
- Burhannuddin, N.L.; Nordin, N.A.; Mazlan, S.A.; Aziz, S.A.A.; Kuwano, N.; Jamari, S.K.M.; Ubaidillah. Physicochemical characterization and rheological properties of magnetic elastomers containing different shapes of corroded carbonyl iron particles. Sci. Rep. 2021, 11, 868. [Google Scholar] [CrossRef] [PubMed]
- Esmaeilnezhad, E.; Choi, H.J.; Schaffie, M.; Gholizadeh, M.; Ranjbar, M. Polymer coated magnetite-based magnetorheological fluid and its potential clean procedure applications to oil production. J. Clean. Prod. 2018, 171, 45–56. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Chung, K.; Liu, C.; Choi, S.B.; Choi, H.J. Formation of core–shell structured complex microparticles during fabrication of magnetorheological elastomers and their magnetorheological behavior. Smart Mater. Struct. 2016, 25, 115028. [Google Scholar] [CrossRef]
- Dong, X.; Ma, N.; Qi, M.; Li, J.; Chen, R.; Ou, J. The pressure-dependent MR effect of magnetorheological elastomers. Smart Mater. Struct. 2012, 21, 075014. [Google Scholar] [CrossRef]
- Jiang, W.; Yao, J.; Gong, X.; Chen, L. Enhancement in magnetorheological effect of magnetorheological elastomers by surface modification of iron particles. Chinese J. Chem. Phys. 2008, 21, 87–92. [Google Scholar] [CrossRef]





| Number of Fatigue Cycles | 0 | Zero-Field | Magnetic Field (300 mT) | ||
|---|---|---|---|---|---|
| 300,000 | 500,000 | 300,000 | 500,000 | ||
| Specific gravity (g/cm3) | 2.586 | 2.581 | 2.583 | 2.577 | 2.565 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, J.-H.; Lee, S.-W.; Bae, S.-H.; Kim, N.-I.; Yun, J.-H.; Jung, J.-H.; Kim, Y.-G. Effect of Cyclic Shear Fatigue under Magnetic Field on Natural Rubber Composite as Anisotropic Magnetorheological Elastomers. Polymers 2022, 14, 1927. https://doi.org/10.3390/polym14091927
Yoon J-H, Lee S-W, Bae S-H, Kim N-I, Yun J-H, Jung J-H, Kim Y-G. Effect of Cyclic Shear Fatigue under Magnetic Field on Natural Rubber Composite as Anisotropic Magnetorheological Elastomers. Polymers. 2022; 14(9):1927. https://doi.org/10.3390/polym14091927
Chicago/Turabian StyleYoon, Jeong-Hwan, Seung-Won Lee, Seok-Hu Bae, Nam-Il Kim, Ju-Ho Yun, Jae-Hum Jung, and Young-Gil Kim. 2022. "Effect of Cyclic Shear Fatigue under Magnetic Field on Natural Rubber Composite as Anisotropic Magnetorheological Elastomers" Polymers 14, no. 9: 1927. https://doi.org/10.3390/polym14091927
APA StyleYoon, J.-H., Lee, S.-W., Bae, S.-H., Kim, N.-I., Yun, J.-H., Jung, J.-H., & Kim, Y.-G. (2022). Effect of Cyclic Shear Fatigue under Magnetic Field on Natural Rubber Composite as Anisotropic Magnetorheological Elastomers. Polymers, 14(9), 1927. https://doi.org/10.3390/polym14091927