Balloons and Quadcopters: Intercomparison of Two Low-Cost Wind Profiling Methods
Abstract
:1. Introduction
2. Methods
2.1. Study Area and Research Campaign
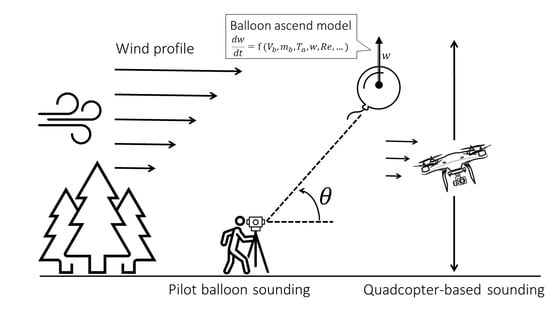
2.2. Balloon Sounding
2.3. Quadcopter-Based Measurements of the Wind Speed and Direction
2.4. Verification of Quadcopter Wind Measurements versus Ground-Based Observations
3. Results
3.1. Calibration of the Drone Wind Measurements versus Ground-Based Observations
3.2. Comparison between Vertical Wind Profiles, Obtained by Two Methods
4. Discussion: What Are the Sources of Discrepancies between Two Methods?
- (1)
- The model, that is used to derive the height of acceding balloon uses a number of parameterizations e.g., drag coefficient dependence on Reynolds number of uncertain accuracy.
- (2)
- As shown in Section 2.2., the other source of errors of the balloon-estimated wind speed and direction is uncertainty of measuring balloons’ angular coordinates by the theodolite, where both errors caused by construction of theodolite and those of the observer come in play; the errors, permitted by construction are 0.2° in vertical and horizontal angles, which translates to 0.1–1 m/s standard error of measured wind speed (Section 2.2 and Section 3.2); this error magnitude, however, does not explain deviations between two methods in a number of cases.
- (3)
- The balloon wind sounding method assumes the absence of vertical air motion, which is actually present leading to errors in computed wind profile [60]; in a case of this study, significant vertical velocities might have been generated in a convective boundary layer (CBL) over polynya; we estimated CBL thickness to be several dozens of meters, while above CBL stratification was stable and significant vertical velocities (i.e., comparable to balloon velocity) in the lower atmosphere were unlikely.
- (4)
- Other uncertainties related with observing balloon in the theodolite can be related with inaccurate theodolite installation and with irregular time intervals between actual angle measurements.
- (5)
- Limitations and uncertainties of the drone’s built-in wind estimation algorithm are not fully understood; however, a correction multiplier may be derived when comparing drone wind measurements to data of sonic anemometers, which noticeably improves the agreement between drones and anemometers, and between drones and balloons.
- (6)
- Airflow in the ABL is non-stationary, which may result in significant differences between the profiles measured with a time lag of few minutes. This may be especially important since the drone-based and balloon-based soundings are difficult to synchronize.
- (7)
- Additional uncertainties may arise from the horizontal displacement of locations of wind measurements by drones and balloons. While the drone measures the wind along a vertical profile over a given site, balloon is blown away for hundreds of meters from the launch point (Figure 10); this is likely to be especially important for the measurements over inhomogeneous landscape with high horizontal variability of wind field.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows, Their Structure and Measurements; Oxford University Press: New York, NY, USA; Oxford, UK, 1994. [Google Scholar]
- Baklanov, A.; Grisogono, B. Atmospheric Boundary Layers: Nature, Theory and Applications to Environmental Modelling and Security; Springer: New York, NY, USA, 2007. [Google Scholar]
- Holtslag, A.A.M.; Svensson, G.; Baas, P.; Basu, S.; Beare, B.; Beljaars, A.C.M.; Bosveld, F.C.; Cuxart, J.; Lindvall, J.; Steeneveld, G.J.; et al. Stable atmospheric boundary layers and diurnal cycles: Challenges for weather and climate models. Bull. Am. Meteorol. Soc. 2013, 94, 1691–1706. [Google Scholar] [CrossRef]
- Barskov, K.V.; Chernyshev, R.V.; Stepanenko, V.M.; Repina, I.A.; Artamonov, A.Y.; Guseva, S.P.; Gavrikov, A.V. Experimental study of heat and momentum exchange between a forest lake and the atmosphere in winter. IOP Conf. Ser. Earth Environ. Sci. 2017, 96, 012003. [Google Scholar] [CrossRef]
- Barskov, K.; Stepanenko, V.; Repina, I.; Artamonov, A.; Gavrikov, A. Two Regimes of Turbulent Fluxes Above a Frozen Small Lake Surrounded by Forest. Bound.-Layer Meteorol. 2019, 173, 311–320. [Google Scholar] [CrossRef]
- Kral, S.; Reuder, J.; Vihma, T.; Suomi, I.; O’Connor, E.; Kouznetsov, R.; Wrenger, B.; Rautenberg, A.; Urbancic, G.; Jonassen, M.; et al. Innovative Strategies for Observations in the Arctic Atmospheric Boundary Layer (ISOBAR)—The Hailuoto 2017 Campaign. Atmosphere 2018, 9, 268. [Google Scholar] [CrossRef] [Green Version]
- Pfotzer, G. History of the use of balloons in scientific experiments. Space Sci. Rev. 1972, 13, 199–242. [Google Scholar] [CrossRef]
- Ingleby, B. An Assessment of Different Radiosonde Types 2015/2016; ECMWF Technical Memoranda; ECMWF: Reading, UK, 2017; p. 69. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Seidel, D.J.; Hunt, D.C. Comparing radiosonde and COSMIC atmospheric profile data to quantify differences among radiosonde types and the effects of imperfect collocation on comparison statistics. J. Geophys. Res. Atmos. 2010, 115, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Durre, I.; Vose, R.S.; Wuertz, D.B. Overview of the integrated global radiosonde archive. J. Clim. 2006, 19, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Peña, A.; Floors, R.; Sathe, A.; Gryning, S.-E.; Wagner, R.; Courtney, M.S.; Larsén, X.G.; Hahmann, A.N.; Hasager, C.B. Ten Years of Boundary-Layer and Wind-Power Meteorology at Høvsøre, Denmark. Bound.-Layer Meteorol. 2016, 158, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Novitskii, M.A.; Mazurin, N.F.; Kulizhnikova, L.K.; Kalinicheva, O.Y.; Tereb, L.A.; Nechaev, D.R.; Sapronov, V.L. Comparison of wind measurements by means of industrially produced sodar and high-altitude meteorological mast in Obninsk. Russ. Meteorol. Hydrol. 2011, 36, 693–699. [Google Scholar] [CrossRef]
- Gilman, G.W.; Coxhead, H.B.; Willis, F.H. Reflection of Sound Signals in the Troposphere. J. Acoust. Soc. Am. 1946, 18, 274–283. [Google Scholar] [CrossRef]
- Kallistratova, M.A. Acoustic and radio-acoustic remote sensing studies in C.I.S. (Former U.S.S.R.)-current status. Int. J. Remote Sens. 1994, 15, 251–266. [Google Scholar] [CrossRef]
- Coulter, R.L.; Kallistratova, M.A. The Role of Acoustic Sounding in a High-Technology Era. Meteorol. Atmos. Phys. 1999, 71, 3–13. [Google Scholar] [CrossRef]
- Kallistratova, M.A.; Petenko, I.V.; Kouznetsov, R.D.; Kulichkov, S.N.; Chkhetiani, O.G.; Chunchusov, I.P.; Lyulyukin, V.S.; Zaitseva, D.V.; Vazaeva, N.V.; Kuznetsov, D.D.; et al. Sodar Sounding of the Atmospheric Boundary Layer: Review of Studies at the Obukhov Institute of Atmospheric Physics, Russian Academy of Sciences. Izvestiya Atmos. Ocean. Phys. 2018, 54, 242–256. [Google Scholar] [CrossRef]
- Emeis, S. Upper limit for wind shear in stably stratified conditions expressed in terms of a bulk Richardson number. Meteorol. Z. 2017, 26, 421–430. [Google Scholar] [CrossRef]
- Banakh, V.; Smalikho, I. Lidar Studies of Wind Turbulence in the Stable Atmospheric Boundary Layer. Remote Sens. 2018, 10, 1219. [Google Scholar] [CrossRef] [Green Version]
- Baker, W.E.; Atlas, R.; Cardinali, C.; Clement, A.; Emmitt, G.D.; Gentry, B.M.; Hardesty, R.M.; Källén, E.; Kavaya, M.J.; Langland, R.; et al. Lidar-Measured Wind Profiles: The Missing Link in the Global Observing System. Bull. Am. Meteorol. Soc. 2014, 95, 543–564. [Google Scholar] [CrossRef]
- Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Weitkamp, C. (Ed.) Springer Science & Business: Berlin/Heidelberg, Germany, 2005; ISBN 0 387 40075 3. [Google Scholar]
- Chanin, M.L.; Garnier, A.; Hauchecorne, A.; Porteneuve, J. A Doppler lidar for measuring winds in the middle atmosphere. Geophys. Res. Lett. 1989, 16, 1273–1276. [Google Scholar] [CrossRef]
- Rees, D.; McDermid, I.S. Doppler lidar atmospheric wind sensor: Reevaluation of a 355-nm incoherent Doppler lidar. Appl. Opt. 1990, 29, 4133. [Google Scholar] [CrossRef] [PubMed]
- Frehlich, R.G.; Kavaya, M.J. Coherent laser radar performance for general atmospheric refractive turbulence. Appl. Opt. 1991, 30, 5325. [Google Scholar] [CrossRef]
- Boquet, M.; Royer, P.; Cariou, J.P.; Machta, M.; Valla, M. Simulation of Doppler lidar measurement range and data availability. J. Atmos. Ocean. Technol. 2016, 33, 977–987. [Google Scholar] [CrossRef]
- Liu, Z.; Barlow, J.F.; Chan, P.W.; Fung, J.C.H.; Li, Y.; Ren, C.; Mak, H.W.L.; Ng, E. A review of progress and applications of pulsed DopplerWind LiDARs. Remote Sens. 2019, 11, 2522. [Google Scholar] [CrossRef] [Green Version]
- Mikkelsen, T. Lidar-based research and innovation at DTU wind energy—A review. J. Phys. Conf. Ser. 2014, 524. [Google Scholar] [CrossRef]
- Hildebrand, J.; Baumgarten, G.; Fiedler, J.; Lübken, F.J. Wind measurements with the ALOMAR RMR-Lidar: Method description and initial results. In Proceedings of the 19th ESA Symposium on European Rocket and Balloon Programmes and Related Research, Bad Reichenhall, Germany, 7–11 June 2009; pp. 7–11. [Google Scholar]
- Woodman, R.F.; Guillen, A. Radar Observations of Winds and Turbulence in the Stratosphere and Mesosphere. J. Atmos. Sci. 1974, 31, 493–505. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Cui, Y.; Zheng, H.; Zhang, T. Wind shear identification with the retrieval wind of doppler wearth radar. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII–3, 2553–2555. [Google Scholar] [CrossRef] [Green Version]
- Muschinski, A.; Lehmann, V.; Justen, L.; Teschke, G. Advanced radar wind profiling. Meteorol. Z. 2005, 14, 609–625. [Google Scholar] [CrossRef]
- Teschke, G.; Lehmann, V. Mean wind vector estimation using the velocity-Azimuth display (VAD) method: An explicit algebraic solution. Atmos. Meas. Tech. 2017, 10, 3265–3271. [Google Scholar] [CrossRef] [Green Version]
- Lyulyukin, V.; Kallistratova, M.; Zaitseva, D.; Kuznetsov, D.; Artamonov, A.; Repina, I.; Petenko, I.; Kouznetsov, R.; Pashkin, A. Sodar observation of the ABL structure and waves over the black sea offshore site. Atmosphere 2019, 10, 811. [Google Scholar] [CrossRef] [Green Version]
- Segales, A.R.; Greene, B.R.; Bell, T.M.; Doyle, W.; Martin, J.J.; Pillar-Little, E.A.; Chilson, P.B. The CopterSonde: An insight into the development of a smart unmanned aircraft system for atmospheric boundary layer research. Atmos. Meas. Tech. 2020, 13, 2833–2848. [Google Scholar] [CrossRef]
- Bell, T.; Greene, B.; Klein, P.; Carney, M.; Chilson, P. Confronting the Boundary Layer Data Gap: Evaluating New and Existing Methodologies of Probing the Lower Atmosphere. Atmos. Meas. Tech. Discuss. 2019, 1–23. [Google Scholar] [CrossRef]
- Roldán, J.J.; Joossen, G.; Sanz, D.; del Cerro, J.; Barrientos, A. Mini-UAV based sensory system for measuring environmental variables in greenhouses. Sensors 2015, 15, 3334–3350. [Google Scholar] [CrossRef] [Green Version]
- Patel, P.N.; Patel, M.A.; Faldu, R.M.; Dave, Y.R. Quadcopter for Agricultural Surveillance. Adv. Electron. Electr. Eng. 2013, 3, 427–432. [Google Scholar]
- Ajayi, O.G.; Salubi, A.A.; Angbas, A.F.; Odigure, M.G. Generation of accurate digital elevation models from UAV acquired low percentage overlapping images. Int. J. Remote Sens. 2017, 38, 3113–3134. [Google Scholar] [CrossRef]
- Voskresensky, I.S.; Suchilin, A.A.; Ushakova, L.A.; Shaforostov, V.M.; Entin, A.L.; Ivanov, M.M. Study of the landslide morphology based on GNSS data and airborne sounding (on the example of a section of the Protva river valley) (in Russian). Eng. Surv. 2018, 12, 50–57. [Google Scholar] [CrossRef]
- Cimoli, E.; Marcer, M.; Vandecrux, B.; Bøggild, C.E.; Williams, G.; Simonsen, S.B. Application of Low-Cost UASs and Digital Photogrammetry for High-Resolution Snow Depth Mapping in the Arctic. Remote Sens. 2017, 9, 1144. [Google Scholar] [CrossRef] [Green Version]
- Nishar, A.; Richards, S.; Breen, D.; Robertson, J.; Breen, B. Thermal infrared imaging of geothermal environments and by an unmanned aerial vehicle (UAV): A case study of the Wairakei-Tauhara geothermal field, Taupo, New Zealand. Renew. Energy 2016, 86, 1256–1264. [Google Scholar] [CrossRef]
- Li, F.; Yang, W.; Liu, X.; Sun, G.; Liu, J. Using high-resolution UAV-borne thermal infrared imagery to detect coal fires in Majiliang mine, Datong coalfield, Northern China. Remote Sens. Lett. 2018, 9, 71–80. [Google Scholar] [CrossRef]
- DeMario, A.; Lopez, P.; Plewka, E.; Wix, R.; Xia, H.; Zamora, E.; Gessler, D.; Yalin, A. Water Plume Temperature Measurements by an Unmanned Aerial System (UAS). Sensors 2017, 17, 306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Konrad, T.G.; Hill, M.L.; Rowland, J.R.; Meyer, J.H. A Small, Radio-Controlled Aircraft as A Platform for Meteorological Sensors. APL Tech. Dig. 1970, 10, 11–19. [Google Scholar]
- Spiess, T.; Bange, J.; Buschmann, M.; Vörsmann, P. First application of the meteorological Mini-UAV “M2AV”. Meteorol. Z. 2007, 16, 159–169. [Google Scholar] [CrossRef]
- Boer, G.; Ivey, M.; Schmid, B.; Lawrence, D.; Dexheimer, D.; Mei, F.; Hubbe, J.; Bendure, A.; Hardesty, J.; Shupe, M.D.; et al. A bird’s-eye view: Development of an operational ARM unmanned aerial capability for atmospheric research in arctic Alaska. Bull. Am. Meteorol. Soc. 2018, 99, 1197–1212. [Google Scholar] [CrossRef]
- Wildmann, N.; Bernard, S.; Bange, J. Measuring the local wind field at an escarpment using small remotely-piloted aircraft. Renew. Energy 2017, 103, 613–619. [Google Scholar] [CrossRef]
- Reuder, J.; Brisset, P.; Jonassen, M.; Müller, M.; Mayer, S. The Small Unmanned Meteorological Observer SUMO: A new tool for atmospheric boundary layer research. Meteorol. Z. 2009, 18, 141–147. [Google Scholar] [CrossRef]
- Varentsov, M.I.; Yu Artamonov, A.; Pashkin, A.D.; Repina, I.A. Experience in the quadcopter-based meteorological observations in the atmospheric boundary layer. IOP Conf. Ser. Earth Environ. Sci. 2019, 231, 012053. [Google Scholar] [CrossRef]
- Jonassen, M.O.; Tisler, P.; Altstädter, B.; Scholtz, A.; Vihma, T.; Lampert, A.; König-Langlo, G.; Lüpkes, C. Application of remotely piloted aircraft systems in observing the atmospheric boundary layer over Antarctic sea ice in winter. Polar Res. 2015, 34, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Lampert, A.; Altstädter, B.; Bärfuss, K.; Bretschneider, L.; Sandgaard, J.; Michaelis, J.; Lobitz, L.; Asmussen, M.; Damm, E.; Käthner, R.; et al. Unmanned Aerial Systems for Investigating the Polar Atmospheric Boundary Layer—Technical Challenges and Examples of Applications. Atmosphere 2020, 11, 416. [Google Scholar] [CrossRef] [Green Version]
- Rautenberg, A.; Schön, M.; zum Berge, K.; Mauz, M.; Manz, P.; Platis, A.; van Kesteren, B.; Suomi, I.; Kral, S.T.; Bange, J. The Multi-Purpose Airborne Sensor Carrier MASC-3 for Wind and Turbulence Measurements in the Atmospheric Boundary Layer. Sensors 2019, 19, 2292. [Google Scholar] [CrossRef] [Green Version]
- Neumann, P.P.; Bartholmai, M. Real-time wind estimation on a micro unmanned aerial vehicle using its inertial measurement unit. Sens. Actuators A Phys. 2015, 235, 300–310. [Google Scholar] [CrossRef]
- Palomaki, R.T.; Rose, N.T.; van den Bossche, M.; Sherman, T.J.; De Wekker, S.F.J. Wind estimation in the lower atmosphere using multirotor aircraft. J. Atmos. Ocean. Technol. 2017, 34, 1183–1191. [Google Scholar] [CrossRef]
- Wilgan, K.; Stauffer, R.; Meindl, M.; Geiger, A. Comparison of tropospheric parameters from Meteodrone measurements with GNSS estimates from ground-based stations. Adv. Space Res. 2020. [Google Scholar] [CrossRef]
- Lee, T.R.; Buban, M.; Dumas, E.; Baker, C.B. Correction: On the use of rotary-wing aircraft to sample near-surface thermodynamic fields: Results from recent field campaigns (Sensors (2019), 19(1), 10). Sensors 2019, 19, 2197. [Google Scholar] [CrossRef] [Green Version]
- Shah, A.; Allen, G.; Pitt, J.R.; Ricketts, H.; Williams, P.I.; Helmore, J.; Finlayson, A.; Robinson, R.; Kabbabe, K.; Hollingsworth, P.; et al. A Near-Field Gaussian Plume Inversion Flux Quantification Method, Applied to Unmanned Aerial Vehicle Sampling. Atmosphere 2019, 10, 396. [Google Scholar] [CrossRef] [Green Version]
- Stepanenko, V.M.; Debolsky, A.; Varentsov, M.I.; Kuznetsov, D.; Zimin, M. Study of Atmospheric Convection Over the Arctic Ice Opening Applying Supercomputer Computations and High Resolution Satellite Data [in Russian]. Earth from Space 2011, 10, 52–55. [Google Scholar]
- Carlson, L.A.; Horn, W.J. New thermal and trajectory model for high-altitude balloons. J. Aircr. 1983, 20, 500–507. [Google Scholar] [CrossRef]
- Wang, J.; Bian, J.; Brown, W.O.; Cole, H.; Grubišić, V.; Young, K. Vertical Air Motion from T-REX Radiosonde and Dropsonde Data. J. Atmos. Ocean. Technol. 2009, 26, 928–942. [Google Scholar] [CrossRef]
- Gallice, A.; Wienhold, F.G.; Hoyle, C.R.; Immler, F.; Peter, T. Modeling the ascent of sounding balloons: Derivation of the vertical air motion. Atmos. Meas. Tech. 2011, 4, 2235–2253. [Google Scholar] [CrossRef] [Green Version]
- Harstad, E. Analysis of Balloon Trajectory Prediction Methods. In Proceedings of the Academic High Altitude Conference 2012, Nashville, TN, USA, 27–29 June 2012; pp. 103–108. [Google Scholar]
- Zhang, J.; Chen, H.; Zhu, Y.; Shi, H.; Zheng, Y.; Xia, X.; Teng, Y.; Wang, F.; Han, X.; Li, J.; et al. A Novel Method for Estimating the Vertical Velocity of Air with a Descending Radiosonde System. Remote Sens. 2019, 11, 1538. [Google Scholar] [CrossRef] [Green Version]
- Jacobi, C.; Scherf, A.; Siemer, A.H.; Roth, R. On the influence of sensor inertia on the estimation of turbulent fluxes from aircraft measurements. Bound.-Layer Meteorol. 1995, 76, 97–108. [Google Scholar] [CrossRef]
- Andreas, E.L.; Claffey, K.J.; Makshtas, A.P. Low-level atmospheric jets and inversions over the western Weddell Sea. Bound.-Layer Meteorol. 2000, 97, 459–486. [Google Scholar] [CrossRef]
- González-Rocha, J.; Woolsey, C.A.; Sultan, C.; De Wekker, S.F.J. Sensing wind from quadrotor motion. J. Guid. Control Dyn. 2019, 42, 836–852. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varentsov, M.; Stepanenko, V.; Repina, I.; Artamonov, A.; Bogomolov, V.; Kuksova, N.; Marchuk, E.; Pashkin, A.; Varentsov, A. Balloons and Quadcopters: Intercomparison of Two Low-Cost Wind Profiling Methods. Atmosphere 2021, 12, 380. https://doi.org/10.3390/atmos12030380
Varentsov M, Stepanenko V, Repina I, Artamonov A, Bogomolov V, Kuksova N, Marchuk E, Pashkin A, Varentsov A. Balloons and Quadcopters: Intercomparison of Two Low-Cost Wind Profiling Methods. Atmosphere. 2021; 12(3):380. https://doi.org/10.3390/atmos12030380
Chicago/Turabian StyleVarentsov, Mikhail, Victor Stepanenko, Irina Repina, Arseniy Artamonov, Vasiliy Bogomolov, Natalia Kuksova, Ekaterina Marchuk, Artem Pashkin, and Alexander Varentsov. 2021. "Balloons and Quadcopters: Intercomparison of Two Low-Cost Wind Profiling Methods" Atmosphere 12, no. 3: 380. https://doi.org/10.3390/atmos12030380
APA StyleVarentsov, M., Stepanenko, V., Repina, I., Artamonov, A., Bogomolov, V., Kuksova, N., Marchuk, E., Pashkin, A., & Varentsov, A. (2021). Balloons and Quadcopters: Intercomparison of Two Low-Cost Wind Profiling Methods. Atmosphere, 12(3), 380. https://doi.org/10.3390/atmos12030380