1. Introduction
With modern day society’s strong reliance on GNSS for both navigation and timing, scintillation caused by ionospheric irregularities can induce loss of lock and increase navigation errors [
1,
2,
3], thereby seriously impacting our technological infrastructure [
4]. While ground-based GNSS receivers are most severely perturbed by equatorial plasma bubbles (EPBs) [
5], sporadic-E (E
) is the leading cause of spaced-based GNSS cycle slips from an E-region ionospheric irregularity [
6]. Sporadic-E manifests as enhanced ion layers caused by metallic ion convergence through neutral wind shears [
7,
8]. The sporadic-E layers are typically referred to as “clouds” because of their non-uniform, patchy nature. The E
impact on radio wave propagation, in terms of over-the-horizon radar and global positioning system (GPS) timing for low Earth orbit (LEO) satellites, relies not only on the presence of sporadic-E but also on the specific characteristics.
Many methods for measuring or characterizing E
have been proposed and implemented in previous studies, including incoherent scatter radars (ISRs) [
9], ionosondes [
10,
11,
12,
13,
14,
15], and global navigation satellite system (GNSS) radio occultation (RO) [
16,
17]. While ISR measurements provide detailed information on the sporadic-E layers, the limited number of global sites and measurement cadence inhibit statistical analyses of E
layers. Ionosondes provide direct measurements of sporadic-E intensity and height, but layer characteristics such as length or vertical thickness are difficult to obtain, given the spatial separation between ground sites and the vertical orientation of the measurements.
GNSS-RO has shown promise for monitoring [
17,
18,
19] and characterizing [
20,
21,
22] sporadic-E layers due to the relatively thin vertical structures that significantly perturb GNSS signals as they propagate horizontally across the ionosphere to a LEO satellite. This geometry allows for characterization of sporadic-E using GNSS-RO, while the relatively long horizontal lengths require exceptionally strong layers to observe in ground-based GNSS sensors [
23]. While the large number of global GNSS-RO measurements with high spatiotemporal resolutions (see [
24] for more detail) provides a unique method for characterizing global E
characteristics and patterns, the amplitude and phase measurements are often difficult to interpret because of the integrated nature of the observations [
25,
26].
To help with the interpretation of GNSS-RO observations of sporadic-E, multiple-phase screen simulations of the signal perturbation have guided the mapping of sporadic-E characteristics to amplitude perturbations [
17,
20,
27]. As shown in the simulations, the magnitude of amplitude fluctuations in terms of a scintillation index such as S
are strong functions of the sporadic-E layer’s vertical thickness, length, intensity (foEs), and orientation. While the vertical thickness can be estimated from GNSS-RO observations [
20], the length and intensity are both unknown from GNSS-RO measurements alone, which makes the intensity estimates uncertain [
25]. However, simulations can help in our understanding of the complex mapping between the layer properties and observed GNSS-RO signals.
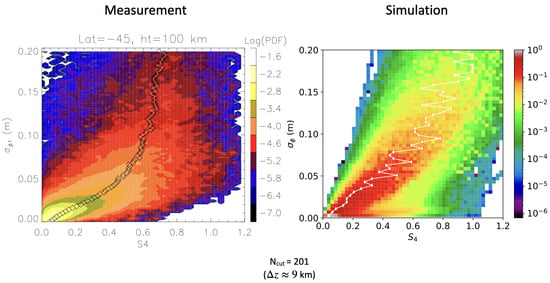
Here, we provide a statistical view of GNSS-RO scintillation observations in terms of the phase standard deviation and amplitude scintillation index S over a month-long period over the mid-latitudes during the local summer at an E-layer altitude of 100 km. Then, to help interpret the results, we simulate GNSS-RO signals after traversing sporadic-E layers in an attempt to reproduce the measured data. Ultimately, we are able to reproduce many of the unique trends from the observations using standard E distributions for length, intensity, and vertical thickness with the assumption that the E layer acts as a Gaussian lens. Finally, inclusion of turbulence to the idealized Gaussian lens helps to improve the agreement between the simulation and measurements.
3. Gaussian Lens Simulations
To model the scintillation observed in the RO data (
Figure 2), the E
characteristics from previous studies were randomly sampled with the assumption that the layer acted as a perturbing Gaussian lens. An analytic solution for the electric field pattern following a Gaussian lens follows
where
E is the complex electric field,
,
is the dimensionless transverse coordinate, and
is the dimensionless coordinate in the propagation direction [
36]. Here,
is the
thickness for the lens and
is the wavenumber. The Gaussian lens in the transverse plane follows
where
is the phase contribution from the lens and
is the peak lens strength [
36]. For our simulations, we used an upper limit of
to calculate the complex electric field at a distance of
km after the lens, which is characteristic of RO geometry and the distance traveled to the LEO satellite after reaching the tangent point. A transverse resolution of
was used for the simulations, where
was the L
wavelength.
While the assumption of a Gaussian lens profile for a sporadic-E layer is certainly an oversimplification, it provides a method to quickly simulate a variety of E
lengths, thicknesses, and strengths to analyze the general trends. The complex, turbulent structures observed by incoherent scatter radars [
37,
38] will provide additional variability and will be explored in
Section 4.
The sporadic-E parameters were derived from previous studies for the length, thickness, tilt, and intensity. The length follows a lognormal distribution with a mode of 170 km and
[
39]. We also reduced the lengths by 65%, following the geometry argument in [
27] for randomly slicing through sporadic-E layers with horizontal lengths of ∼10 times the horizontal thickness.
The vertical thicknesses follow a lognormal distribution with a mode of 1.5 km and
[
20]. This vertical thickness corresponds to the thickness where the signal intensity reaches 95% of the background intensity within the typical u-shape profile observed for E
. As observed in
Figure 3 and
Figure 4, the Gaussian lens is generally thinner than the u-shaped intensity dip, especially for the moderate and stronger lenses. This increase in thickness for the intensity profiles is caused by the negative lens, which diverges the signal away from the lens at large distances. While the relationship between the 95% intensity definition of thickness from [
20] and the Gaussian lens thickness defined for simulations is rather complex and requires more research to fully understand, here, we define the vertical thickness as the altitude range between the points where the phase reaches 20% of the lens peak. This 20% value was selected instead of the full width at 1/e to reduce the lens thicknesses and match the observed S
-
trends in
Figure 2. Additional research is required to properly map the thicknesses derived in [
20] to Gaussian lens thicknesses for simulation or observation. However, this simple mapping provides a starting point for simulation of GNSS-RO statistical observations.
Sporadic-E intensities in the form of foEs were taken from [
22], assuming a Gaussian profile with a mean of ∼3 MHz and a standard deviation of ∼1 MHz (estimated from Figures 8 and 9 in [
22]). The background E-layer density should be taken into account to properly capture the lens strength magnitudes through conversion of the foEs to an fo
Es, as outlined in [
40], where fo
Es refers to the metal plasma critical frequency of the E
layer. However, we did not explicitly convert the foEs to an fo
Es here, as we found that the foEs intensity distribution from [
22] provided a decent match to the observed S
-
scintillation trends. Furthermore, as fo
Es calculations require knowledge of the local E-layer densities at the time and location of measurement, it is difficult to calculate an fo
Es distribution directly from an foEs distribution without additional information. We hope that the statistical approach outlined here helps provide insight into fo
Es distributions by providing a method for adjusting the distribution to improve agreement between simulations and observations.
The E
parameters were converted to effective Gaussian lenses using
where
is the index of refraction at the center of the E
layer,
l is the horizontal length of the layer,
is the GPS L
frequency of 1575.42 MHz, and
k is the L
wavenumber. With
,
, which creates a negative lens. Here, we ignored the background ionosphere to simplify the simulations, and the E
tilts were not included to focus on the moderate-to-strong scintillation trends. As shown in [
20], layer tilts significantly reduced the amplitude scintillation at the LEO measurement plane, which introduced additional data points near the origin of our S
-
histograms. As these points did not significantly contribute to the moderate-to-strong scintillation trends observed in
Figure 2, they were ignored for this analysis.
3.1. Simulation Examples
Examples of the Gaussian lens simulations are displayed in
Figure 3 and
Figure 4 for the phase and intensity of the GPS L
signal, respectively, as measured at the LEO measurement plane after propagating through a sporadic-E layer with a vertical thickness of 1.5 km. Three varying lens strengths are displayed to show the different scintillation responses, using a 2.2 km window (N
= 51) to calculate S
and
. The lens strengths were −1 rad (−3 cm), −5 rad (−15 cm), and −10 rad (−30 cm), showing weak, moderate, and strong lensing, respectively. For perspective, the −5 rad lens strength may correspond to an E
layer with a 3.4 MHz foEs and a length of 65 km. As observed in
Figure 3, the measured signal phase closely tracked the Gaussian lens for the weak and moderate lenses, but significant phase scintillation reduced the measured phase for the strong lens. Interestingly, while the scintillation on the edges of the lens was most severe for the strong lens, the largest
was observed for the moderate lens scenario with a peak of ∼6 cm. This counter-intuitive result was due to the large phase gradient from the lens that was mostly captured by the moderate lens, but it was less severe for the strong lens because of the phase scintillation observed at the edges, which reduced the peak phase measured in the lens. These results indicate that thin, strong lenses can produce relatively low peak
values, but the phase scintillation at the edges of the lenses will be enhanced.
The signal intensities at the LEO measurement plane for the same lenses are displayed in
Figure 4. Here, the characteristic U-shaped profile described in [
20] is present for the moderate and strong lenses, where the low intensity region at the bottom of the U shape was caused by the negative lensing effect of the E
layers. Additionally, the ringing around the u-shape fade is due to diffraction [
20]. However, the weak lens did not produce a strong diffraction pattern, and only the beginning of a U-shaped pattern was present. S
showed elevated peaks of 1.3 for the moderate lens and 1.5 for the strong lens, with a relatively low peak of approximately 0.3 for the weak lens. In the center of the moderate and strong profiles, the S
magnitude was elevated by the decreased intensity mean at the center of the U-shaped profile. For the S
techniques calculated using a longer running average of the background intensity, such as those provided by the COSMIC Data Analysis and Archive Center (CDAAC) [
28], the S
calculated over one-second intervals (50 points for 50 Hz data) would be nearly equal to the standard deviation of the normalized intensity.
Following the results from [
27], the peak S
plateaued for the moderate-to-strong lenses, and the roughly linear peak S
relationship with the lens strength was mostly observed for the weak-to-moderate lenses. Additionally, the vertical lens thickness played a large role in the phase and amplitude scintillation, with thinner lenses generally causing more scintillation in both phase and amplitude. However, as discussed previously,
also depends on the large phase perturbation induced directly by the E
layer and not strictly the scintillation from diffraction. These examples help to interpret the statistical results outlined below.
3.2. Simulated Statistics
In an attempt to reproduce the observations displayed in
Figure 2, the E
length, vertical thickness, and foEs distributions were randomly sampled 10,000 times, and the resulting electric field profiles in the LEO measurement plane (
km) were stored for each of the 10,000 simulations. Histograms of the sampling along with the distributions are displayed in
Figure 5a for the length,
Figure 5b for the vertical thickness, and
Figure 5c for the foEs.
Joint S
-
histograms of the simulated S
and
at the LEO measurement plane are displayed in
Figure 6. Each grid point in the measurement plane was used as a single data point to create the histogram. Extremely low values (below 0.001) were removed for both S
and
to improve readability. The majority of points occurred in the region of S
and
m, corresponding to weak intensity and phase fluctuations, respectively. This region corresponds to the weak lens simulations in
Figure 3 and
Figure 4.
Outside of this weak lens region, there were three regions of interest. The first most noticeable region was caused by significant phase scintillation with elevated S
and low
. When strong phase scintillation occurred, the peak phase perturbation magnitude was reduced, which in turn reduced the
peak, as displayed in
Figure 3. In this region, both phase and amplitude scintillation are important, and techniques such as those outlined in [
17,
19,
22] will work well, while techniques relying on phase perturbation alone will struggle with properly characterizing the layer. With the exception of the 2.2 km window, the simulations showed significant counts in this region while the observations (
Figure 2) did not. This indicates that the simulations were oversampling the strong-thin regions, and a method to reduce this sampling is presented in
Section 5.
The second region of interest was produced by the moderate lenses, resulting in a roughly linear increase in
with respect to S
. For the 2.2 km window, this moderate lens zone was much weaker than the strong scintillation zone, but the strong scintillation linear trend from the origin to S
,
m roughly matched the observations in
Figure 2. The moderate lens region was more obvious for the 5.0 km and 9.0 km windows, with a
slope of 0.05/0.6 m for both windows. These slopes were in line with the observed slopes from the origin to
m, although the observations showed a slightly elevated slope of 0.05/0.5 m for the 9.0 km window.
However, the simulated moderate lens region extended throughout S
, which was not observed in the GNSS-RO measurements. Instead,
Figure 2 shows the S
plateau between 0.6 and 0.8. This difference was likely due to the assumption of a Gaussian lens for the E
layers, which was certainly an oversimplification, as shown by the incoherent scatter radar measurements (e.g., [
37,
38]). The realistic E
layers were patchy and billowy, which was caused by the Kelvin–Helmholtz instability [
41], reducing the ideal strong lensing and also introducing additional perturbations and scintillation caused by the billows. The Gaussian lens’s focusing diffraction pattern is capable of producing very large peak intensity scintillation, while the billowy layers from turbulence are not capable of producing the same focusing. This important point will be explored further in
Section 4.
Finally, the third zone of interest was characterized by elevated
and low S
(
Figure 6a) due to thicker layers with relatively weak lens strengths. These thicker, weaker layers caused phase perturbations without causing significant diffraction in the signal intensity. The GPS-RO techniques relying on phase perturbation (e.g., [
18,
25]) will work well in this region, while the techniques relying on the signal intensity (e.g., [
19,
22]) will have difficulty characterizing these thicker, weaker layers.
While the simulations reported here were strictly for GNSS-RO geometries, it must be noted that many previous studies have compared and validated RO techniques for monitoring sporadic-E with ground-based ionosondes [
19,
21,
25,
26]. The foEs distribution [
22] was derived from RO observations with an empirical fit to ionosonde measurements, and the length distribution was taken from a topside sounder (Explorer 20) [
39]. There is certainly room for improvement in GNSS-RO techniques for monitoring sporadic-E, but the general agreement with ground-based sensors provides confidence in the results obtained only from GNSS-RO observations.
4. Simulations Including Turbulence
Following [
42], the spectral density function
for random variations in the index of refraction
can be described by
where
is the refractive index variance and
is the Shkarofsky [
43] spectral density function:
Here,
corresponds to the inner scale (smallest structure),
corresponds to the outer scale (largest structure),
is the modified Bessel function, and
is the power law index parameter. Additionally, we have
where
is the turbulent strength parameter.
To include a turbulence spectrum into our simulations, we used the following conditions:
rad/m,
rad/m where
is the vertical thickness of the layer,
for the Kolmogorov turbulence, and
. A Kolmogorov power law was selected based on the results in [
44], and the value of
was adjusted to improve the simulations agreement with the observations displayed in
Figure 2 while also producing vertical refractivity profiles with variations similar to those observed for the horizontally integrated E
profiles from the ISR measurements as displayed in [
37]. This turbulence was added to the initial Gaussian lens by generating complex frequency samples of the Shkarofsky spectrum using a normal distribution with a standard deviation of one and a mean of zero for both the real and imaginary components. The Fourier transform of these spectral random realizations provided random fluctuations in space that were added to the original Gaussian lens to provide a turbulent sporadic-E layer:
where
is the two-dimensional index of refraction with the inclusion of turbulence,
is the original refractive index profile, and
is the random index of refraction variation in the vertical (transverse) direction. Here, we used the same vertical
for all
z in the horizontal (propagation) direction to focus on vertical lens irregularities.
Example phase and amplitude profiles for turbulent lenses are displayed in
Figure 7 and
Figure 8. The same lens strengths of −1, −5, and −10 radians used for the Gaussian lenses in
Figure 3 and
Figure 4 are analyzed here. However, the vertical thickness was increased to 2.5 km to clearly see the turbulence. The phase profiles showed similar behavior to the Gaussian lenses, with the exception of reduced phase scintillation for the −10 radian lens due to the thicker vertical thickness that reduced the overall vertical gradient in the index of refraction. A slight asymmetry was observed for the −10 radian lens, with a stronger asymmetry observed for the −5 rad lens. While the phase profiles were similar to the Gaussian lenses, the amplitude profiles were significantly perturbed (
Figure 8). This was most obvious for the −5 and −10 radian lenses, which showed large asymmetries in the idealized U-shaped profiles. This asymmetry was a result of the asymmetric lens caused by the inclusion of turbulence. The asymmetric U-shaped profile presented here is commonly measured in GNSS-RO observations (e.g.,
Figure 1), resulting from the small scale structures observed in E
layers. Additionally, the strong S
caused by lens focusing was reduced in the turbulent lenses because of the lens imperfections. This reduced focusing ultimately resulted in the S
plateau observed in
Figure 1.
It must be noted here that many GNSS-RO observations of sporadic-E show multiple layers [
45]. These multi-layered structures result in either multiple U shapes or a blend caused by the interference of the two diffraction patterns. Examples of these multi-layered profiles can be found in previous studies (e.g.,
Figure 3 of [
20]) and throughout the CDAAC catalog (e.g., atmPhs_C001.2010.029.01.35.G14_2010.2640_nc and atmPhs_C002.2008.001.00. 28.G04_2013.3520_nc). The simplified modeling approach taken here did not account for these multi-layered structures, as we were focused on the scintillation produced by single layers. While the multi-layered events with sufficient altitude spread would not change the scintillation statistics of the individual layers, the interfering diffraction patterns were not accounted for in this study.
After the turbulence was added to the Gaussian lens, an analytic solution to the electric field (i.e., Equation (
3) for the Gaussian lens) no longer existed, and the electric field at the GNSS-RO measurement plane had to be calculated using a numerical technique. Here, we used the multiple-phase screen approach due to the long propagation distance of 3000 km after the perturbing layer. This multiple-phase screen approach is commonly used for RO propagation through sporadic-E layers [
17,
20,
27], and more information on the technique can be found in [
42,
46]. Specifically, we used a transverse (vertical) grid spacing of 76 cm (four L
wavelengths) for a total transverse length of 50 km. In the propagation (horizontal) direction, we took 1000 equal steps through the E
layer followed by ∼20 km steps after the layer for a total propagation distance of 3000 km.
Using the same distributions implemented for
Figure 6 with the addition of turbulence provided the results displayed in
Figure 9. The linear slopes were similar to the slopes observed for the Gaussian lens, but plateauing of S
better matched the observations (
Figure 2). This was due to a reduction in the Gaussian lenses focusing with the lens “imperfections” added by the turbulence. Additionally, the 9.0 km window
slope from the origin was increased to 0.05/0.5 m, which matched the observed slope better than the Gaussian lens simulations. The similarity of these simulations to the observations supports previous sporadic-E measurements that showed the turbulent nature of these layers [
37,
38]. Including a relatively small degree of turbulence in our simulations provided more realistic sporadic-E layers and improved our agreement with the GNSS-RO observations.
While the inclusion of turbulence helped to reduce the high and S region caused by focusing, the strong phase scintillation region with strong S and low remained more enhanced than the observations suggest. Similar to the Gaussian lens results, the 2.2 km window showed reasonable agreement with the observed slopes from the origin, but the 5.0 and 9.0 windows did not show this enhancement. This implies that we were oversampling the strong, thin layers with large vertical gradients in the index of refraction, and some physical limitation on the coupled E characteristics may have existed that was unaccounted for in our uncoupled random sampling.
5. Diffusion-Limited
The region of elevated S
and low
observed in our simulations (
Figure 6 and
Figure 9) was not present in the observations displayed in
Figure 2, indicating that the strong, thin layers were oversampled from the length, strength, and vertical distributions. To limit the number of strong, thin lenses in an attempt to improve agreement with the observations, we removed the randomly sampled layers with
rad/km
. This threshold value was obtained by averaging the ratios obtained for the
values, where various vertical thicknesses in the range of
km began to show significant phase scintillation. Here, we define significant phase scintillation as a peak measured phase difference of greater than 30% from the applied phase, illustrated by the black and red lines in
Figure 3. Physically, this limit on
may be related to a diffusion limited layer as
at the center of the layer, where
is the diffusion coefficient for metal ions,
is the metal ion density, and
x is in the vertical direction. Ion convergence caused by wind shears is counteracted by this vertical diffusion such that the final layer characteristics will be dependent on both processes [
8]. Layers that become too strong and thin will experience elevated diffusion that will ultimately place a limit on the allowed
ratio.
Using this diffusion limit on the randomly sampled distributions resulted in the remaining parameters displayed in
Figure 10. Out of the 10,000 initial samples, 4383 layers with
rad/km
were removed. Compared with
Figure 5, the layers with elevated values for length or foEs (
is proportional to the length-foEs
product) and low
were removed from the distributions.
The simulated S
-
histograms for these diffusion-limited layers are displayed in
Figure 11. Compared with the original distributions used to create
Figure 6, the strong phase scintillation region with elevated S
and low
was greatly reduced. Similarly, the S
-
histograms for the turbulent lenses were also improved by the removal of layers with
rad/km
(
Figure 12). While the strong phase scintillation region was not completely removed in the simulations, inclusion of the diffusion-limited threshold on the
ratio significantly improved agreement with the observations.
The threshold enforced here was selected to show a proof of concept, but placing physical thresholds on the randomly sampled distributions should be enforced to ensure that unrealistic sporadic-E layers are not produced. Determination of these thresholds requires insight into the coupling between each of the parameters, which we treated as independent up to this point. Alternatively, the reduction of longer, thinner, and stronger layers may indicate that the E
distributions used here require adjustment to match the observations. For the length distribution, the authors of [
23] found that strong layers have a median length of 100 km, which is a reduction from the 170 km mode used here from [
39]. Additionally, taking the background E-layer into account through a conversion of foEs to fo
Es as outlined in [
40] would help to reduce the effective lens strengths, since
length-foEs
. Certainly, additional research is warranted to help improve the E
distributions and to determine the coupling characteristics.
6. Conclusions
A statistical view of GNSS-RO phase and amplitude scintillation at an E-region altitude in the mid-latitudes during the local summer indicates that sporadic-E is likely the primary cause of the unique S- trends. The GNSS-RO observations showed a nearly linear trend in joint two-dimensional S- histograms until the S saturated near 0.8. To understand the trends, 10,000 RO simulations through sporadic-E layers were performed using length, intensity, and vertical thickness distributions from previous research with the assumption that the E layer acted as a Gaussian lens. This simplified view of the layers provides insight into different scintillation statistics for weak, moderate, and strong lenses.
Using the Gaussian lens assumption, a roughly linear slope from the origin to m was observed in both the observations and simulations. In the simulations, this trend was produced strictly by E layers, which implies that the observed GNSS-RO scintillation was also likely caused by E. While the Gaussian layer simulations showed agreement with the primary trends, a region of elevated and S was present in the simulations but not the observations. This elevated S- was caused by focusing from these idealized lenses. In reality, the E layers were turbulent and billowy. Therefore, we included Kolmogorov turbulence by adding random realizations of a Shkarofsky spectral density function to perturb the idealized Gaussian lenses. The addition of these random turbulence fluctuations made the E layers more physically realistic, which in turn improved agreement with the observations by removing the large number of points in the elevated and S region. Additionally, a plateau of S was produced by these turbulent layers, which better matched the observed trends.
Simulations using the original distributions without constraints on the coupled layer parameters showed large counts with significant phase scintillation (elevated S and low ) produced by strong, thin lenses. This strong phase scintillation region was not present in the observations, which indicated an oversampling of these strong, thin layers. To reduce this oversampling, a threshold was placed on the ratio which was proportional to the ion diffusion rates. After placing a limit on this ratio, counts in the elevated S and low region were significantly reduced, resulting in better agreement with the observations and implying that there may be a diffusion limit on E layers. The improvement was best illustrated by the 2.2 km window simulations, likely due to the narrow window being more sensitive to small-scale phase fluctuations.
This research provides a new method for interpreting GNSS-RO results in bulk through large numbers of simulations guided by predefined probability distribution functions. For future work, the distributions can be adjusted to find the best fits to the statistical observations and improve our understanding of the sporadic-E layer characteristics. However, it must be noted that certain ambiguities arise with respect to the length × foEs product contributing to the strength of the lens, and the diffraction pattern is also highly dependent on the lens thickness, which requires physically realistic bounds and starting points placed on the distributions using previous E measurements. Improving the turbulence estimates and implementation can also help improve agreement and provide insight into the complex layer structure. Finally, it may be possible to apply this approach to equatorial and polar observations to enhance characterization of the ionospheric disturbances in these regions. While the scale sizes, general characteristics, and challenges of equatorial and polar observations are markedly different than those for mid-latitude E, a statistical scintillation approach taking advantage of RO geometry provides a complementary dataset to the traditional ground-based GNSS measurements.