Concept of Soil Moisture Ratio for Determining the Spatial Distribution of Soil Moisture Using Physiographic Parameters of a Basin and Artificial Neural Networks (ANNs)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
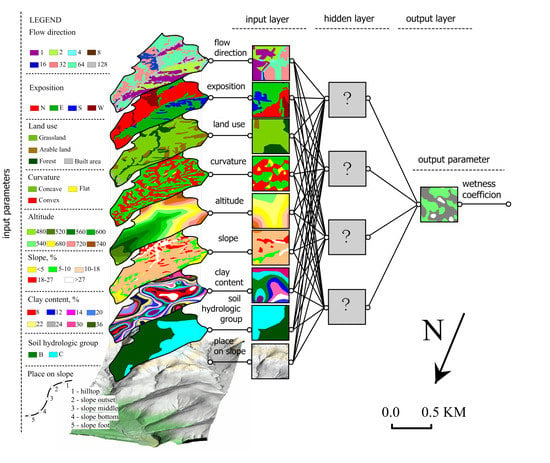
2.2. Experimental Design/Models Applied
2.3. Statistical Analysis and Data Procedure
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Islam, S. Estimation of root zone soil moisture and surface fluxes partitioning using near surface soil moisture measurement. J. Hydrol. 2002, 259, 1–14. [Google Scholar] [CrossRef]
- Romana, N. Soil moisture at local scale: Measurements and simulations. J. Hydrol. 2014, 516, 6–20. [Google Scholar] [CrossRef]
- Castillo, V.M.; Gómez-Plaza, A.; Martinez-Mena, M. The role of antecendent soil water content in the runoff response of a semiarid catchment: A simulation approach. J. Hydrol. 2003, 284, 114–130. [Google Scholar] [CrossRef]
- Western, A.W.; Zhou, S.L.; Grayson, R.B.; McMahon, T.A.; Blöschl, G.; Wilson, D.J. Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes. J. Hydrol. 2004, 286, 113–134. [Google Scholar] [CrossRef]
- Boroń, K.; Klatka, S.; Ryczek, M.; Liszka, P. Kształtowanie się właściwości fizycznych, fizykochemicznych i wodnych rekultywowanego i niezrekultywowanego osadnika byłych Krakowskich Zakładów Sodowych “Solvay”/The formation of the physical, physico-chemical and water properties reclaimed and not reclaimed sediment reservoir of the former Cracow Soda Plant “Solvay”. Acta Sci. Pol. Form. Circumiectus 2016, 15, 35–43. [Google Scholar] [CrossRef]
- Brocca, L.; Morbidelli, R.; Melone, F.; Moramaraco, T. Soil moisture spatial variability in experimental areas of central Italy. J. Hydrol. 2007, 333, 356–373. [Google Scholar] [CrossRef]
- Klatka, S.; Malec, M.; Ryczek, M.; Boroń, K. Wpływ działalności eksploatacyjnej Kopalni Węgla Kamiennego “Ruch Borynia” na gospodarkę wodną wybranych gleb obszaru górniczego/Influence of mine activity of the coal mine “Ruch Borynia” on water management of chosen soils on mining area. Acta Sci. Pol. Form. Circumiectus 2015, 14, 115–125. Available online: http://www.formatiocircumiectus.actapol.net/tom14/zeszyt1/14_1_115.pdf (accessed on 24 February 2021). [CrossRef]
- Klatka, S.; Malec, M.; Ryczek, M.; Kruk, E.; Zając, E. Ocena zdolności retencyjnych wybranych odpadów przemysłowych/Evaluation of retention ability of chosen industrial wastes. Acta Sci. Pol. Form. Circumiectus 2016, 15, 53–60. Available online: http://www.formatiocircumiectus.actapol.net/tom15/zeszyt4/15_4_53.pdf (accessed on 15 January 2021).
- Wei, J.B.; Xiao, D.N.; Zeng, H.; Fu, Y.K. Spatial variability of soil properties in relation to land use and topography in a typical small watershed of the black soil region, northeastern China. Environ. Geol. 2008, 53, 1663–1672. [Google Scholar] [CrossRef]
- Boron, K.; Klatka, S.; Ryczek, M.; Zając, E. Reclamation and cultivation of the Cracow soda plant lagoons, International Conference on Construction for a Sustainable Environment, Vilnius, LITHUANIA, JUL 01–04, 2008. In Construction for a Sustainable Environment, 1st ed.; Sarsby, R., Ed.; Routledge: London, UK, 2010; pp. 245–250. Available online: https://www.routledge.com/Construction-for-a-Sustainable-Environment/Sarsby-Meggyes/p/book/9780415566179 (accessed on 20 July 2021).
- Nikolopulos, E.I.; Anagnostou, E.N.; Borga, M.; Vivoni, E.R.; Papadopoulos, A. Sensitivity of a mountain basin flash flood to initial wetness condition and rainfall variability. J. Hydrol. 2011, 402, 165–178. [Google Scholar] [CrossRef]
- Santra, P.; Sankar, B.; Chakravarty, D. Spatial prediction of soil properties in a watershed scale through maximum likelihood approach. Environ. Earth Sci. 2012, 65, 2051–2061. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Crow, W.T.; Robertson, D.E. The impacts of assimilating satellite soil moisture into a rainfall-runoff model in a semi-arid catchment. J. Hydrol. 2014, 519, 2763–2773. [Google Scholar] [CrossRef]
- Kruk, E.; Klapa, P.; Ryczek, M.; Ostrowski, K. Influence of DEM Elaboration Methods on the USLE Model Topographical Factor Parameter on Steep Slopes. Remote Sens. 2020, 12, 3540. [Google Scholar] [CrossRef]
- Tischler, M.; Garcia, M.; Peters-Lidard, C.; Moran, M.S.; Miller, S.; Kumar, S.; Geiger, J. A GIS framework for surface-layer soil moisture estimation combining satellite radar measurements and land surface modeling with soil physical property estimation. Environ. Model. Softw. 2007, 22, 891–898. [Google Scholar] [CrossRef]
- Vidhya Lakshmi, S.; Jijo, J.; Soundariya, S.; Vishalini, T.; Kasinatha Pandian, P. A comparison of Soil Texture Distribution and Soil Moisture Mapping of Chennai Coast using Landsat ETM+ and IKONOS Data. CONFERENCE ON WATER RESOURCES, COASTAL AND OCEAN ENGINEERING (ICWRCOE 2015). Aquat. Procedia 2015, 4, 1452–1460. [Google Scholar] [CrossRef]
- Gómez-Plaza, A.; Martinez-Mena, M.; Albaladejo, J.; Castillo, V.M. Factors regulating spatial distribution of soil water content in small semiarid catchments. J. Hydrol. 2001, 253, 211–226. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, Y.; Luo, Y. Assessing Hydrological Connectivity Mitigated by Reservoirs, Vegetation Cover, and Climate in Yan River Watershed on the Loess Plateau, China: The Network Approach. Water 2020, 12, 1742. [Google Scholar] [CrossRef]
- Tombul, M. Mapping Field Surface Soil Moisture for Hydrological Modeling. Water Resour. Manag. 2007, 21, 1865–1880. [Google Scholar] [CrossRef]
- Gou, W.; Wang, C.; Ma, T.; Zeng, X.; Yang, H. A distributed Grid-Xinanjiang model with integration of subgrid variability of soil storage capacity. Water Sci. Eng. 2016, 9, 97–105. [Google Scholar]
- Zhang, C.; Liu, S.; Fang, J.; Tan, K. Research on the spatial variability of soil moisture based on GIS. In Computer and Computing Technologies in Agriculture, Volume I, The International Federation for Information Processing, Vol. 258, Proceedings of the First IFIP TC 12 International Conference on Computer and Computing Technologies in Agriculture (CCTA 2007), Wuyishan, China, 18–20 August 2007; Li, D., Ed.; Springer: Boston, MA, USA, 2008; pp. 719–727. [Google Scholar] [CrossRef] [Green Version]
- Merdun, H.; Meral, R.; Riza Demirkiran, A. Effect of the initial soil moisture content on the spatial distribution of the water retention. Eurasian Soil Sci. 2008, 41, 1098–1106. [Google Scholar] [CrossRef]
- Penna, D.; Borga, M.; Norbiato, D.; Dalla Fontana, G. Hillslope scale soil moisture variability in a steep alpine terrain. J. Hydrol. 2009, 364, 311–327. [Google Scholar] [CrossRef]
- Temimi, M.; Leconte, R.; Chaouch, N.; Sukumal, P.; Khanbilvardi, R.; Brissette, F. A combination of remote sensing data and topographic attributes for the spatial and temporal monitoring of soil wetness. J. Hydrol. 2010, 388, 28–40. [Google Scholar] [CrossRef]
- Fan, Y.; Zhang, C.; Fang, J.; Tian, L. Research on Regional Spatial Variability of Soil Moisture Based on GIS. In Computer and Computing Technologies in Agriculture III, IFIP Advances in Information and Communication Technology, Proceedings of the Third IFIP TC 12 International Conference (CCTA 2009), Beijing, China, 14–17 October 2009; Li, D., Zhao, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 317, pp. 466–470. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.H.; Shao, M.A.; Jia, X.X. Spatial pattern of soil moisture and its temporal stability within profiles on a loessial slope in northwestern China. J. Hydrol. 2013, 495, 150–161. [Google Scholar] [CrossRef]
- Halecki, W.; Kruk, E.; Ryczek, M. Loss of topsoil and soil erosion by water in agricultural areas: A multi-criteria approach for various land use scenarios in the Western Carpathians using a SWAT model. Land Use Policy 2018, 73, 363–372. [Google Scholar] [CrossRef]
- Halecki, W.; Kruk, E.; Ryczek, M. Evaluation of Soil Erosion in the Mątny Stream Catchment in the West Carpathians Using the G2 model. Catena 2018, 164, 116–124. [Google Scholar] [CrossRef]
- Soil Survey Staff. Soil Taxonomy; USDA: Washington, DC, USA, 1975; pp. 17–754. [Google Scholar]
- Hillier, A. Manual for Working with ArcGIS10. Unpublished Paper. Available online: http://works.bepress.com/amy_hillier/24/ (accessed on 13 December 2020).
- Wilson, D.J.; Gallant, J.C. Digital terrain analysis. In Terrain Analysis: Principles and Applications; Wilson, D.J., Gallant, J.C., Eds.; John Willey & Sons, Inc.: New York, NY, USA, 2000; pp. 1–27. [Google Scholar]
- USDA—Natural Resources Conservation Service. National Soil Survey Handbook, Title 430-VI; US Department of Agriculture, Natural Resources Conservation Service: Washington, DC, USA, 2002. [Google Scholar]
- Silveira, M.C.F.; Oliveira, E.M.M.; Carvajal, E.; Bon, E.P.S. Nitrogen regulation of Saccharomyces cerevisiae invertase. Role of the URE2 gene. Appl. Biochem. Biotechnol. 2000, 84–86, 247–254. [Google Scholar] [CrossRef]
- United States Department of Agriculture. Soil Conservation Service 1993. In National Engineering Handbook; Section 4, Hydrolohy; Washington, DC, USA. Available online: https://directives.sc.egov.usda.gov/OpenNonWebContent.aspx?content=43924.wba (accessed on 20 July 2021).
- Svetlitchnyi, A.A.; Plotnitskiy, S.V.; Stepovaya, O.Y. Spatial distribution of soil moisture content within catchments and its modelling on the basis of topographic data. J. Hydrol. 2003, 277, 50–60. [Google Scholar] [CrossRef]
- Kruk, E.; Ryczek, M.; Malec, M.; Klatka, S. Kształtowanie się współczynnika wilgotności gleby w zlewni potoku Mątny w Gorcach/Shaping of the wetness coefficient in the Mątny stream basin in the Gorce mountains. Inżynieria Ekologiczna 2016, 50, 99–105. [Google Scholar] [CrossRef] [Green Version]
- Dawson, J.F.; Richter, A.W. Probing three-way interactions in moderated multiple regression: Development and application of a slope difference test. J. Appl. Psychol. 2006, 91, 917–926. [Google Scholar] [CrossRef]
- Rajurkar, M.P.; Kothyari, U.C.; Chaube, U.C. Artificial neural networks for daily rainfall-runoff modelling. Hydrol. Sci. J. 2002, 47, 865–877. [Google Scholar] [CrossRef]
- Caamaño, D.; Googwin, P.; Manic, M. Derivation of a bedload sediment transport formula using artificial neural networks. In Proceedings of the 7th International Conference on Hydroinformatics HIC, Nice, France, 4–8 September 2006; pp. 1–8. [Google Scholar]
- Kentel, E. Estimation of river flow by artificial neural networks and identification of input vectors susceptible to producing unreliable flow estimates. J. Hydrol. 2009, 375, 481–488. [Google Scholar] [CrossRef]
- Lepš, J.; Smilauer, P. Multivariate Analysis of Ecological Data Using CANOCO; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Rahnama, M.B.; Barani, G.A. Application of rainfall-runoff models to Zard River catchments. Am. J. Environ. Sci. 2005, 1, 86–89. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Risse, L.M.; Nearing, M.A. Evaluation of WEPP and its comparison with USLE and RUSLE. Trans. ASAE 2000, 43, 1129–1135. [Google Scholar] [CrossRef]
- Gebregiorgis, M.F.; Savage, M.J. Field, laboratory and estimated soil-water content limits. Water SA 2006, 32, 155–162. [Google Scholar] [CrossRef] [Green Version]







| Parameter | Explanation | |
|---|---|---|
| DEM | Geodesic and Cartographic Documentation Centre | Scale 1:5000, resolution 5 m |
| Altitude | meters mean sea level | m.a.s.l. |
| Slope | Differences of heights between the points Δh divided by length of projection of direction between the points, l; [%] 1 | Intervals, %:0–5; 5–10; 10–18; 18–27; >27 |
| Flow direction | Determined based on height difference between the given cell determined each of the eight adjacent cells, based on one-direction points model D8 2 [31], where: Z is the number of adjacent cells, h is the resolution of the GRID model, hØ(i) is the distance between the middle points of cell, 1 for the ones situated in the cardinal directions (N,E,S,W), root square for the two remaining ones. |  Convention of the DEM numbering (a) in standard cell system, (b) in determination of flow directions, (c) coding of flow directions by the D8 algorithm [31] |
| Exposition | Location on the slope with respect to the direction of sunlight rays, determined using a 4-grade scale, as one of the geographical directions. | East–E, west–W, north–N, south–S |
| Shape of the slope | Concave, flat, convex | |
| Situation on a slope | Determined using a five-grade scale: hilltop, slope outset, slope middle, slope bottom, slope foot |  |
| Digital soil map | Institute of Soil Science and Plant Cultivation State Research Institute | Scale 1:25,000 |
| Hydrological soil group | Determined based on U.S. Department of Agriculture–Natural Resources Conservation Service [32] method | Groups:A, B, C, D |
| Use | Orthophoto map; site inspection | Scale 1:1000Data: 25.07.2014 |
| Clay fraction | Determined using the Casagrande’a method. Soil samples were collected from a top layer of the soil (0 to 10 cm) in 43 selected study plots. |  |
| AMC Classes | Vegetative Dormant Season | Vegetative Growing Season |
|---|---|---|
| I | Less than 12.7 | Less than 35.5 |
| II | 12.7 to 28.0 | 35.5 to 53.3 |
| III | More than 28 | More than 53.3 |
| Measure | Equation |
|---|---|
| Mean error of prediction | MEP 1 |
| Root mean square error | RMSE 2 |
| Mean percentage error | MPE 3 |
| Model efficiency | ME 4 |
| Quality | learning | 0.757 |
| testing | 0.752 | |
| validation | 0.807 | |
| Error | learning | 0.006 |
| testing | 0.009 | |
| validation | 0.004 | |
| Perceptron activation functions | hidden | |
| output |
| No. | Parameter | Relative Sensitivity | Absolute Influence [%] |
|---|---|---|---|
| 1 | Place on slope | 11.3 | 40 |
| 2 | Exposition | 3.5 | 12 |
| 3 | Use | 3.0 | 11 |
| 4 | Shape of the slope | 2.9 | 10 |
| 5 | Altitude | 2.9 | 10 |
| 6 | Flow direction | 1.6 | 5.0 |
| 7 | Slope | 1.3 | 5.0 |
| 8 | Clay fraction | 1.0 | 4 |
| 9 | Hydrological group | 1,0 | 4 |
| Model Efficiency Measures. | ||||
|---|---|---|---|---|
| MEP | RMSE | MPE [%] | ME [-] | R2 [-] |
| 0.004 | 0.104 | −0.6 | 0.580 | 0.581 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kruk, E.; Fudała, W. Concept of Soil Moisture Ratio for Determining the Spatial Distribution of Soil Moisture Using Physiographic Parameters of a Basin and Artificial Neural Networks (ANNs). Land 2021, 10, 766. https://doi.org/10.3390/land10070766
Kruk E, Fudała W. Concept of Soil Moisture Ratio for Determining the Spatial Distribution of Soil Moisture Using Physiographic Parameters of a Basin and Artificial Neural Networks (ANNs). Land. 2021; 10(7):766. https://doi.org/10.3390/land10070766
Chicago/Turabian StyleKruk, Edyta, and Wioletta Fudała. 2021. "Concept of Soil Moisture Ratio for Determining the Spatial Distribution of Soil Moisture Using Physiographic Parameters of a Basin and Artificial Neural Networks (ANNs)" Land 10, no. 7: 766. https://doi.org/10.3390/land10070766
APA StyleKruk, E., & Fudała, W. (2021). Concept of Soil Moisture Ratio for Determining the Spatial Distribution of Soil Moisture Using Physiographic Parameters of a Basin and Artificial Neural Networks (ANNs). Land, 10(7), 766. https://doi.org/10.3390/land10070766