Spontaneous and Controlled Macroscopic Chiral Symmetry Breaking by Means of Crystallization
Abstract
:1. Context, Introduction
1.1. Chiral Discrimination between Pairs of Enantiomers in the Solid State
1.2. Equilibrium in Solution
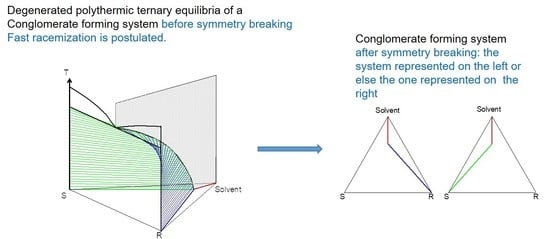
2. Macroscopic Spontaneous Chiral Symmetry Breaking Induced by Crystallization
Deracemization Induced by a Flux of Energy Crossing the Suspension (DIFECS)
- (i)
- A large solubility difference between the racemic composition (poorly soluble) and the pure enantiomer (much more soluble) is necessary. The alpha molar ratio, α = s(±)/s(+) = s(±)/s(−), is thus very small (this constitutes another contrast with preferential crystallization for which α is usually comprised between: √(2) and 2). Various analyses of racemic solutions in different solvents led to the surmised existence of solvated homochiral assemblies.
- (ii)
- For a globally racemic composition, the crystal structure permits a certain degree of disorder between homochiral chains and/or planes, even if single crystals obtained from poorly supersaturated racemic solution (e.g., point Ω1.2 in Figure 8 representing a supersaturation C/CSAT = 1.2) could have their structures resolved by X-ray diffraction in centrosymmetric space groups such as P-1 (the most frequent for PE) or P21/c. However, crystals obtained under high supersaturation (i.e., from a clear solution represented by point Ω8 in Figure 8) clearly reveal, by Second Harmonic Generation (SHG), homochiral domains. If this effect cannot be detected, PE experiments fail [48].
- (iii)
- The first generation of compounds showing PE effect have all exhibited solid–solid transitions between various disordered phases. For the second generation of compounds showing PE effect in some cases, no such solid–solid transition could be detected. A solid–solid transition during PE does not appear anymore as a mandatory condition for its success.
- (iv)
- From the first solid crystallized, which can have a high degree of stacking faults, a selective dissolution of domains containing the same enantiomer as that in excess in the solution occurs. A unique, detailed study [49] has shown that this dissolution is actually concomitant to the re-incorporation of the opposition enantiomer. It is thus the exchange of opposite enantiomers that is likely to be a concerted process. This results in a clear enrichment of the mother liquor and, simultaneously, a slight enrichment of the solid phase in the opposite enantiomer At the end of PE, the solid phase appears to be composed of Heterogeneous Nearly-Racemic Crystals (HNRC). This is different from a genuine solid solution (i.e., mixed crystals) where a random distribution of the two enantiomeric molecules is observed over the crystallographic sites. In HNRC, there are some homochiral domains of sub-micron to micron sizes.
- (v)
- The HNRC could remain kinetically stable for months without a return to stable equilibrium if the system remains unstirred in a quiescent state.
3. Control of Macroscopic Chiral Symmetry Breaking by Means of Crystallization
4. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
List of Symbols and Abbreviations
| CSD: | Crystal Size Distribution |
| DIFECS: | Deracemization Induced by a Flux of Energy Crossing the Suspension |
| e.e.: | Enantiomeric excess = (R − S)/(R + S) |
| GRD: | Growth Rate Dispersion |
| HNRC: | Heterogeneous Nearly-Racemic Crystals |
| NPLIN: | Non-Photochemical Laser Induced Nucleation |
| PC: | Preferential Crystallization |
| PE: | Preferential Enrichment |
| SOAT: | Second Order Asymmetric Transformation |
| TCID: | Temperature Cycle-Induced Deracemization |
| US: | Ultrasound |
References
- Coquerel, G. Review on the Heterogeneous Equilibria between Condensed Phases in Binary Systems of Enantiomers. Enantiomer 2000, 5, 481–498. [Google Scholar] [PubMed]
- Clevers, S.; Coquerel, G. Kryptoracemic Compound Hunting and Frequency in the Cambridge Structural Database. CrystEngComm 2020. [Google Scholar] [CrossRef]
- Fábián, L.; Brock, C.P. A List of Organic Kryptoracemates. Acta Crystallogr. B 2010, 66, 94–103. [Google Scholar] [CrossRef] [PubMed]
- Tiekink, E.R.T. Kryptoracemates. In Advances in Organic Crystal Chemistry, Comprehensive Reviews 2020; Springer: Cham, Switzerland, 2020; Chapter 19; pp. 381–404. [Google Scholar]
- Rekis, T. Crystallization of Chiral Molecular Compounds: What Can Be Learned from the Cambridge Structural Database? Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2020, 76, 307–315. [Google Scholar] [CrossRef]
- Bishop, R.; Scudder, M.L. Multiple Molecules in the Asymmetric Unit (Z′ > 1) and the Formation of False Conglomerate Crystal Structures. Cryst. Growth Des. 2009, 9, 2890–2894. [Google Scholar] [CrossRef]
- Dryzun, C.; Avnir, D. On the Abundance of Chiral Crystals. Chem. Commun. 2012, 48, 5874–5876. [Google Scholar] [CrossRef]
- Gubaidullin, A.T.; Samigullina, A.I.; Bredikhina, Z.A.; Bredikhin, A.A. Crystal Structure of Chiral Ortho-Alkyl Phenyl Ethers of Glycerol: True Racemic Compound, Normal, False and Anomalous Conglomerates within the Single Five-Membered Family. CrystEngComm 2014, 16, 6716–6729. [Google Scholar] [CrossRef]
- Druot, S.; Petit, N.; Petit, S.; Coquerel, G.; Chanh, N. Experimental Data and Modelling of the Interactions in Solid State and in Solution between (R) and (S) N -Acetyl-α- Methylbenzylamine. Influence on Resolution by Preferential Crystallization. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. Mol. Cryst. Liq. Cryst. 1996, 275, 271–291. [Google Scholar] [CrossRef]
- Harfouche, L.C.; Brandel, C.; Cartigny, Y.; Ter Horst, J.H.; Coquerel, G.; Petit, S. Enabling Direct Preferential Crystallization in a Stable Racemic Compound System. Mol. Pharm. 2019. [Google Scholar] [CrossRef]
- Belletti, G.; Tortora, C.; Mellema, I.D.; Tinnemans, P.; Meekes, H.; Rutjes, F.P.J.T.; Tsogoeva, S.B.; Vlieg, E. Photoracemization-Based Viedma Ripening of a BINOL Derivative. Chem. Eur. J. 2020, 26, 839–844. [Google Scholar] [CrossRef]
- Wacharine-Antar, S.; Levilain, G.; Dupray, V.; Coquerel, G. Resolution of (±)-Imeglimin-2,4-Dichlorophenylacetate Methanol Solvate by Preferential Crystallization. Org. Process Res. Dev. 2010, 14, 1358–1363. [Google Scholar] [CrossRef]
- Coquerel, G. Solubility of Chiral Species as Function of the Enantiomeric Excess. J. Pharm. Pharmacol. 2015, 67, 869–878. [Google Scholar] [CrossRef] [PubMed]
- Galland, A.; Dupray, V.; Berton, B.; Morin-Grognet, S.; Sanselme, M.; Atmani, H.; Coquerel, G. Spotting Conglomerates by Second Harmonic Generation. Cryst. Growth Des. 2009, 9, 2713–2718. [Google Scholar] [CrossRef]
- Simon, F.; Clevers, S.; Dupray, V.; Coquerel, G. Relevance of the Second Harmonic Generation to Characterize Crystalline Samples. Chem. Eng. Technol. 2015, 38, 971–983. [Google Scholar] [CrossRef]
- Gendron, F.-X.; Mahieux, J.; Sanselme, M.; Coquerel, G. Resolution of Baclofenium Hydrogenomaleate by Using Preferential Crystallization. A First Case of Complete Solid Solution at High Temperature and a Large Miscibility Gap in the Solid State. Cryst. Growth Des. 2019, 19, 4793–4801. [Google Scholar] [CrossRef]
- Coquerel, G.; Tamura, R. “Enantiomeric disorder” pharmaceutically oriented. In Disordered Pharmaceutical Materials; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; pp. 135–160. [Google Scholar] [CrossRef]
- Mbodji, A.; Gbabode, G.; Sanselme, M.; Cartigny, Y.; Couvrat, N.; Leeman, M.; Dupray, V.; Kellogg, R.M.; Coquerel, G. Evidence of Conglomerate with Partial Solid Solutions in Ethylammonium Chlocyphos. Cryst. Growth Des. 2020, 20, 2562–2569. [Google Scholar] [CrossRef]
- Zlokazov, M.V.; Pivnitsky, K.K. Lamellar Conglomerates. Mendeleev Commun. 2020, 30, 1–6. [Google Scholar] [CrossRef]
- Coquerel, G. Chiral discrimination in the solid state: Applications to resolution and deracemization. In Advances in Organic Crystal Chemistry: Comprehensive Reviews 2015; Tamura, R., Miyata, M., Eds.; Springer: Tokyo, Japan, 2015; pp. 393–420. [Google Scholar] [CrossRef]
- Oketani, R.; Marin, F.; Tinnemans, P.; Hoquante, M.; Laurent, A.; Brandel, C.; Cardinael, P.; Meekes, H.; Vlieg, E.; Geerts, Y.; et al. Deracemization in a Complex Quaternary System with a Second-Order Asymmetric Transformation by Using Phase Diagram Studies. Chem. Eur. J. 2019, 25, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Viedma, C. Chiral Symmetry Breaking during Crystallization: Complete Chiral Purity Induced by Nonlinear Autocatalysis and Recycling. Phys. Rev. Lett. 2005, 94, 065504. [Google Scholar] [CrossRef] [Green Version]
- Intaraboonrod, K.; Lerdwiriyanupap, T.; Hoquante, M.; Coquerel, G.; Flood, A.E. Temperature Cycle Induced Deracemization. Mendeleev Commun. 2020, 30, 395–405. [Google Scholar] [CrossRef]
- Rougeot, C.; Guillen, F.; Plaquevent, J.-C.; Coquerel, G. Ultrasound-Enhanced Deracemization: Toward the Existence of Agonist Effects in the Interpretation of Spontaneous Symmetry Breaking. Cryst. Growth Des. 2015, 15, 2151–2155. [Google Scholar] [CrossRef]
- Iggland, M.; Fernández-Ronco, M.P.; Senn, R.; Kluge, J.; Mazzotti, M. Complete Solid State Deracemization by High Pressure Homogenization. Chem. Eng. Sci. 2014, 111, 106–111. [Google Scholar] [CrossRef]
- Cameli, F.; Xiouras, C.; Stefanidis, G.D. Intensified Deracemization via Rapid Microwave-Assisted Temperature Cycling. CrystEngComm 2018, 20, 2897–2901. [Google Scholar] [CrossRef] [Green Version]
- Steendam, R.R.E.; Dickhout, J.; van Enckevort, W.J.P.; Meekes, H.; Raap, J.; Rutjes, F.P.J.T.; Vlieg, E. Linear Deracemization Kinetics during Viedma Ripening: Autocatalysis Overruled by Chiral Additives. Cryst. Growth Des. 2015, 15, 1975–1982. [Google Scholar] [CrossRef]
- Sakamoto, M. Asymmetric synthesis involving dynamic enantioselective crystallization. In Advances in Organic Crystal Chemistry: Comprehensive Reviews 2020; Sakamoto, M., Uekusa, H., Eds.; Springer: Singapore, 2020; pp. 433–456. [Google Scholar] [CrossRef]
- Steendam, R.R.E.; Brouwer, M.C.T.; Huijs, E.M.E.; Kulka, M.W.; Meekes, H.; van Enckevort, W.J.P.; Raap, J.; Rutjes, F.P.J.T.; Vlieg, E. Enantiopure Isoindolinones through Viedma Ripening. Chem. Eur. J. 2014, 20, 13527–13530. [Google Scholar] [CrossRef]
- Viedma, C.; Cintas, P. Homochirality beyond Grinding: Deracemizing Chiral Crystals by Temperature Gradient under Boiling. Chem. Commun. 2011, 47, 12786–12788. [Google Scholar] [CrossRef] [Green Version]
- Suwannasang, K.; Flood, A.E.; Rougeot, C.; Coquerel, G. Using Programmed Heating–Cooling Cycles with Racemization in Solution for Complete Symmetry Breaking of a Conglomerate Forming System. Cryst. Growth Des. 2013, 13, 3498–3504. [Google Scholar] [CrossRef]
- Suwannasang, K.; Flood, A.E.; Coquerel, G. A Novel Design Approach to Scale Up the Temperature Cycle Enhanced Deracemization Process: Coupled Mixed-Suspension Vessels. Cryst. Growth Des. 2016, 16, 6461–6467. [Google Scholar] [CrossRef]
- Suwannasang, K.; Flood, A.E.; Rougeot, C.; Coquerel, G. Use of Programmed Damped Temperature Cycles for the Deracemization of a Racemic Suspension of a Conglomerate Forming System. Org. Process Res. Dev. 2017, 21, 623–630. [Google Scholar] [CrossRef]
- Schindler, M.; Brandel, C.; Kim, W.-S.; Coquerel, G. Temperature Cycling Induced Deracemization of NaClO3 under the Influence of Na2S2O6. Cryst. Growth Des. 2020, 20, 414–421. [Google Scholar] [CrossRef]
- Maggioni, G.M.; Fernández-Ronco, M.P.; Meijden, M.W.v.d.; Kellogg, R.M.; Mazzotti, M. Solid State Deracemisation of Two Imine-Derivatives of Phenylglycine Derivatives via High-Pressure Homogenisation and Temperature Cycles. CrystEngComm 2018, 20, 3828–3838. [Google Scholar] [CrossRef]
- Xiouras, C.; Fytopoulos, A.A.; Ter Horst, J.H.; Boudouvis, A.G.; Van Gerven, T.; Stefanidis, G.D. Particle Breakage Kinetics and Mechanisms in Attrition-Enhanced Deracemization. Cryst. Growth Des. 2018, 18, 3051–3061. [Google Scholar] [CrossRef] [Green Version]
- Uchin, R.; Suwannasang, K.; Flood, A.E. Model of Temperature Cycle-Induced Deracemization via Differences in Crystal Growth Rate Dispersion. Chem. Eng. Technol. 2017, 40, 1252–1260. [Google Scholar] [CrossRef]
- Bodák, B.; Maggioni, G.M.; Mazzotti, M. Population-Based Mathematical Model of Solid-State Deracemization via Temperature Cycles. Cryst. Growth Des. 2018, 18, 7122–7131. [Google Scholar] [CrossRef]
- Uwaha, M. A Model for Complete Chiral Crystallization. J. Phys. Soc. Jpn. 2004, 73, 2601–2603. [Google Scholar] [CrossRef]
- Katsuno, H.; Uwaha, M. Monte Carlo Simulation of a Cluster Model for the Chirality Conversion of Crystals with Grinding. J. Cryst. Growth 2009, 311, 4265–4269. [Google Scholar] [CrossRef]
- Katsuno, H.; Uwaha, M. Mechanism of Chirality Conversion by Periodic Change of Temperature: Role of Chiral Clusters. Phys. Rev. E 2016, 93, 013002. [Google Scholar] [CrossRef] [Green Version]
- Kondepudi, D.K.; Bullock, K.L.; Digits, J.A.; Hall, J.K.; Miller, J.M. Kinetics of Chiral Symmetry Breaking in Crystallization. J. Am. Chem. Soc. 1993, 115, 10211–10216. [Google Scholar] [CrossRef]
- Ni, X.; Shepherd, R.; Whitehead, J.; Liu, T. Chiral Symmetry Breaking Due to Impeller Size in Cooling Crystallization of Sodium Chlorate. CrystEngComm 2018, 20, 6894–6899. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Kaufman, R.J.; Singh, N. Chiral Symmetry Breaking in Sodium Chlorate Crystallizaton. Science 1990, 250, 975–976. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Laudadio, J.; Asakura, K. Chiral Symmetry Breaking in Stirred Crystallization of 1,1′-Binaphthyl Melt. J. Am. Chem. Soc. 1999, 121, 1448–1451. [Google Scholar] [CrossRef]
- Tamura, R.; Takahashi, H.; Coquerel, G. Twenty-Five years’ history, mechanism, and generality of preferential enrichment as a complexity phenomenon. In Advances in Organic Crystal Chemistry, Comprehensive Reviews 2020; Springer: Cham, Switzerland, 2020; Chapter 20; pp. 405–432. [Google Scholar]
- Coquerel, G. Preferential Crystallization. Top. Curr. Chem. 2007, 269, 1–51. [Google Scholar] [CrossRef] [PubMed]
- De Saint Jores, C.; Brandel, C.; Gharbi, N.; Sanselme, M.; Cardinael, P.; Coquerel, G. Limitations of Preferential Enrichment: A Case Study on Tryptophan Ethyl Ester Hydrochloride. Chem. Eng. Technol. 2019, 42, 1500–1504. [Google Scholar] [CrossRef]
- De Saint Jores, C. Towards a Deeper Understanding of Preferential Enrichment. A Case Study: DL Arginine Fumarate in Ethanol-Water 50-50 Mixture. Ph.D. Thesis, University of Rouen, Mont-Saint-Aignan, France, 2019. [Google Scholar]
- Gonnade, R.G.; Iwama, S.; Mori, Y.; Takahashi, H.; Tsue, H.; Tamura, R. Observation of Efficient Preferential Enrichment Phenomenon for a Cocrystal of (Dl)-Phenylalanine and Fumaric Acid under Nonequilibrium Crystallization Conditions. Cryst. Growth Des. 2011, 11, 607–615. [Google Scholar] [CrossRef]
- Gervais, C.; Beilles, S.; Cardinaël, P.; Petit, S.; Coquerel, G. Oscillating Crystallization in Solution between (+)- and (−)-5-Ethyl-5-Methylhydantoin under the Influence of Stirring. J. Phys. Chem. B 2002, 106, 646–652. [Google Scholar] [CrossRef]
- Mbodji, A.; Gbabode, G.; Sanselme, M.; Couvrat, N.; Leeman, M.; Dupray, V.; Kellogg, R.M.; Coquerel, G. Family of Conglomerate-Forming Systems Composed of Chlocyphos and Alkyl-Amine. Assessment of Their Resolution Performances by Using Various Modes of Preferential Crystallization. Cryst. Growth Des. 2019, 19, 5173–5183. [Google Scholar] [CrossRef]
- Potter, G.A.; Garcia, C.; McCague, R.; Adger, B.; Collet, A. Oscillating Crystallization of (+) and (–) Enantiomers during Resolution by Entrainment of 2-Azabicyclo[2.2.1]Hept-5-En-3-One. Angew. Chem. Int. Ed. Engl. 1996, 35, 1666–1668. [Google Scholar] [CrossRef]
- Kern, R. Fundamentals of epitaxy. In Crystal Growth in Science and Technology; Arend, H., Hulliger, J., Eds.; NATO ASI Series; Springer US: Boston, MA, USA, 1989; pp. 143–165. [Google Scholar] [CrossRef]
- Noorduin, W.L.; Izumi, T.; Millemaggi, A.; Leeman, M.; Meekes, H.; Van Enckevort, W.J.P.; Kellogg, R.M.; Kaptein, B.; Vlieg, E.; Blackmond, D.G. Emergence of a Single Solid Chiral State from a Nearly Racemic Amino Acid Derivative. J. Am. Chem. Soc. 2008, 130, 1158–1159. [Google Scholar] [CrossRef] [Green Version]
- Steendam, R.R.E.; Harmsen, B.; Meekes, H.; van Enckevort, W.J.P.; Kaptein, B.; Kellogg, R.M.; Raap, J.; Rutjes, F.P.J.T.; Vlieg, E. Controlling the Effect of Chiral Impurities on Viedma Ripening. Cryst. Growth Des. 2013, 13, 4776–4780. [Google Scholar] [CrossRef]
- Schindler, M. Deracemization of Sodium Chlorate with or without the Influence of Sodium Dithionate. Ph.D. Thesis, University of Rouen, Mont-Saint-Aignan, France, 2020. [Google Scholar]
- Belletti, G.; Meekes, H.; Rutjes, F.P.J.T.; Vlieg, E. Role of Additives during Deracemization Using Temperature Cycling. Cryst. Growth Des. 2018, 18, 6617–6620. [Google Scholar] [CrossRef]
- Hawbaker, N.A.; Blackmond, D.G. Energy Threshold for Chiral Symmetry Breaking in Molecular Self-Replication. Nat. Chem. 2019, 11, 957–962. [Google Scholar] [CrossRef]
- Hein, J.E.; Huynh Cao, B.; Viedma, C.; Kellogg, R.M.; Blackmond, D.G. Pasteur’s Tweezers Revisited: On the Mechanism of Attrition-Enhanced Deracemization and Resolution of Chiral Conglomerate Solids. J. Am. Chem. Soc. 2012, 134, 12629–12636. [Google Scholar] [CrossRef]
- Sheldon, R.A. Chirotechnology: Industrial Synthesis of Optically Active Compounds; Marcel Dekker—CRC Press: New York, NY, USA, 1993. [Google Scholar]
- Oketani, R.; Hoquante, M.; Brandel, C.; Cardinael, P.; Coquerel, G. Resolution of an Atropisomeric Naphthamide by Second-Order Asymmetric Transformation: A Highly Productive Technique. Org. Process Res. Dev. 2019, 23, 1197–1203. [Google Scholar] [CrossRef]
- Boyle, W.J.; Sifniades, S.; Van Peppen, J.F. Asymmetric Transformation of.Alpha.-Amino-.Epsilon.-Caprolactam, a Lysine Precursor. J. Org. Chem. 1979, 44, 4841–4847. [Google Scholar] [CrossRef]
- Black, S.N.; Williams, L.J.; Davey, R.J.; Moffatt, F.; Jones, R.V.H.; McEwan, D.M.; Sadler, D.E. The Preparation of Enantiomers of Paclobutrazol: A Crystal Chemistry Approach. Tetrahedron 1989, 45, 2677–2682. [Google Scholar] [CrossRef]
- Kaptein, B.; Noorduin, W.L.; Meekes, H.; van Enckevort, W.J.P.; Kellogg, R.M.; Vlieg, E. Attrition-Enhanced Deracemization of an Amino Acid Derivative That Forms an Epitaxial Racemic Conglomerate. Angew. Chem. Int. Ed. 2008, 47, 7226–7229. [Google Scholar] [CrossRef]
- Addadi, L.; Van Mil, J.; Lahav, M. Useful Impurities for Optical Resolutions. 2. Generality and Mechanism of the Rule of Reversal. J. Am. Chem. Soc. 1981, 103, 1249–1251. [Google Scholar] [CrossRef]
- Niinomi, H.; Sugiyama, T.; Tagawa, M.; Murayama, K.; Harada, S.; Ujihara, T. Enantioselective Amplification on Circularly Polarized Laser-Induced Chiral Nucleation from a NaClO3 Solution Containing Ag Nanoparticles. CrystEngComm 2016, 18, 7441–7448. [Google Scholar] [CrossRef]













Towards greater departure from equilibrium | Preferential Enrichment | Heterogenous Nearly-Racemic Crystals (HNRC) with possibility of alternating homochiral domains. Largest domains corresponding to the minor enantiomer | 0: Stagnant conditions to stay away from stable equilibrium |  |
 | Kondepudi’s Experiment | Conglomerate forming system Fast racemization in solution or non-chiral entity in solution | Moderate, collision but avoid too strong shearing effects |  |
 | Deracemization Induced by a Flux of Energy Crossing the Suspension (DIFECS): -Ultrasounds -Microwaves -TCID -Viedma Ripening (close to 0) | Conglomerate forming system Fast racemization in solution or non-chiral entity in solution A lamellar conglomerate does not hinder deracemization | From soft to medium for TCID Strong with shearing effect for attrition enhanced i.e., Viedma Ripening |  Towards greater intensity of the mechanical stress |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coquerel, G.; Hoquante, M. Spontaneous and Controlled Macroscopic Chiral Symmetry Breaking by Means of Crystallization. Symmetry 2020, 12, 1796. https://doi.org/10.3390/sym12111796
Coquerel G, Hoquante M. Spontaneous and Controlled Macroscopic Chiral Symmetry Breaking by Means of Crystallization. Symmetry. 2020; 12(11):1796. https://doi.org/10.3390/sym12111796
Chicago/Turabian StyleCoquerel, Gérard, and Marine Hoquante. 2020. "Spontaneous and Controlled Macroscopic Chiral Symmetry Breaking by Means of Crystallization" Symmetry 12, no. 11: 1796. https://doi.org/10.3390/sym12111796
APA StyleCoquerel, G., & Hoquante, M. (2020). Spontaneous and Controlled Macroscopic Chiral Symmetry Breaking by Means of Crystallization. Symmetry, 12(11), 1796. https://doi.org/10.3390/sym12111796