Study on the Temperature Rise Characteristics of Successive Clutch Shifting Considering the Disengaged Friction Pair Gaps
Abstract
:1. Introduction
2. Numerical Model
2.1. Dynamic Model
2.2. Lubrication Model
2.3. Contact Model
2.4. Sliding Model
2.5. Spline Resistance Model
2.6. Piston Impact Model
2.7. Heat Conduction Model
3. Simulation and Verification
3.1. Simulation Method
3.2. Test Conditions
3.3. Model Verification
4. Results and Discussion
4.1. Shifting Interval
4.2. Lubrication Oil Temperature
5. Conclusions
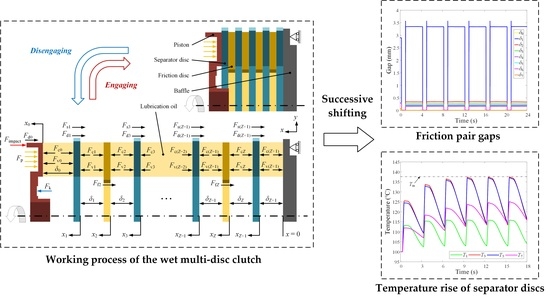
- Because of the attenuation effect of the spline friction force on the applied pressure, the generated friction heat and disengaged friction pair gaps both decayed from the first to the last friction pair in sequence. Thus, both the temperature rise and temperature drop of the second separator disc near the piston were the largest.
- In the successive shifting condition, the convection heat transfer was enhanced with the expansion of the temperature difference between the separator disc and the lubrication oil. When the decreasing temperature rise equaled the increasing temperature drop, the maximum clutch temperature no longer increased.
- Because more heat was dissipated in the disengagement status with the increase of the shifting interval, the accumulated temperature rise decreased exponentially until zero. Moreover, with the increasing lubrication oil temperature, the efficiency of convection heat transfer declined; the temperature rise in a single engaging process increased, but the accumulated temperature rise was not enlarged due to the broadening second and third friction pair gaps.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ared | non-groove area ratio | Toil | temperature of lubrication oil (°C) |
| c | specific heat capacity (J/(kg·°C)) | T∞ | ambient temperature (°C) |
| cs | damping coefficient (N·s/m) | vi | linear velocity of inner annulus (m/s) |
| dm | thickness of friction material (m) | vo | linear velocity of outer annulus (m/s) |
| Di | inner diameter (m) | average velocity of lubrication oil (m/s) | |
| Do | outer diameter (m) | V | linear velocity difference (m/s) |
| e | recovery coefficient | x | displacement (m) |
| effective Young’s modulus (Pa) | ẋ | velocity (m/s) | |
| Fc | contact force (N) | ẍ | acceleration (m/s2) |
| Fd | damping force (N) | Z | number of friction pairs |
| Ff, Fs | spline friction force (N) | αf | pressure angle of inner spline (°) |
| Fimpact | impact force (N) | αs | pressure angle of outer spline (°) |
| Fk | return spring force (N) | β | asperity radius (m) |
| Fp | control oil pressure force (N) | ε | spatial step (m) |
| Fv | hydrodynamic force (N) | δ | gap of friction pair (m) |
| h | nominal oil film thickness (m) | ωf1 | angular velocity of separator disc (rad/s) |
| average oil film thickness (m) | ωf2 | angular velocity of friction disc (rad/s) | |
| Hfd | thickness of friction disc (m) | Δω | angular speed difference (rad/s) |
| Hsd | thickness of separator disc (m) | η | dynamic viscosity (Pa·s) |
| If2 | inertia of drive end (kg·m2) | κ | plastic deformation coefficient |
| K0 | stiffness of impact (N/m) | λ | thermal conductivity (W/(m·°C)) |
| contact coefficient | μspline | spline friction coefficient | |
| m0 | weight of piston (kg) | ξ | local relative indentation (m) |
| m1 | weight of separator disc (kg) | ρ | density (kg/m3) |
| m2 | weight of friction disc (kg) | σ | standard deviation of roughness (m) |
| MR | resistance torque (N·m) | τ | time step (s) |
| MP | motor torque (N·m) | ϕr | pressure flow factor |
| n | impact coefficient | ϕf, ϕfs | shear stress factors |
| N | asperity density (/m2) | Ψ | permeability (m2) |
| P | applied pressure (Pa) | Subscripts | |
| Ri | inner radius of friction pair (m) | ||
| Ro | outer radius of friction pair (m) | fc | Cu-based friction material |
| Rf | pitch radius of inner spline (m) | st | steel material |
| Rs | pitch radius of outer spline (m) | l | lubrication oil |
References
- Bao, H.; Huang, W.; Lu, F. Investigation of engagement characteristics of a multi-disc wet friction clutch. Tribol. Int. 2021, 159, 106940. [Google Scholar] [CrossRef]
- Meng, F.; Xi, J. Numerical and experimental investigation of temperature distribution for dry-clutches. Machines 2021, 9, 185. [Google Scholar] [CrossRef]
- Yu, L.; Ma, B.; Chen, M.; Li, H.; Liu, J.; Zheng, L. Numerical and experimental studies on the characteristics of friction torque based on wet paper-based clutches. Tribol. Int. 2019, 131, 541–553. [Google Scholar] [CrossRef]
- Yu, L.; Ma, B.; Chen, M.; Xue, J.; Zhao, P. Variation mechanism of the friction torque in a Cu-based wet clutch affected by operating parameters. Tribol. Int. 2020, 147, 106169. [Google Scholar] [CrossRef]
- Li, W.; Huang, J.; Fei, J.; Cao, L.; Yao, C.; Wang, W. Simulation of the engagement of carbon fabric wet clutch: Analytical and experimental comparison. Tribol. Int. 2015, 90, 502–508. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Liu, Y.; Zhang, W. Modeling and experimental research on engaging characteristics of wet clutch. Ind. Lubr. Tribol. 2019, 71, 94–101. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, K.; Wu, X. Structural design and friction performance test of a new conical groove friction disks in wet clutch. Appl. Sci. 2021, 11, 7231. [Google Scholar] [CrossRef]
- Yu, L.; Ma, B.; Chen, M.; Li, H.Y.; Liu, J. Experimental study on the friction stability of paper-based clutches concerning groove patterns. Ind. Lubr. Tribol. 2020, 72, 541–548. [Google Scholar] [CrossRef]
- Li, W.; Huang, J.; Fei, J.; Cao, L.; Yao, C. Simulation and application of temperature field of carbon fabric wet clutch during engagement based on finite element analysis. Int. Commun. Heat Mass Transf. 2016, 71, 180–187. [Google Scholar]
- Ma, B.; Yu, L.; Chen, M.; Li, H.Y.; Zheng, L.J. Numerical and experimental studies on the thermal characteristics of the clutch hydraulic system with provision for oil flow. Ind. Lubr. Tribol. 2019, 71, 733–740. [Google Scholar] [CrossRef]
- Wu, J.; Ma, B.; Li, H.; Wang, L. The temperature field of friction disc in wet clutch involving the unconventional heat dissipation on the contact surface. Tribol. Trans. 2021, 64, 1–9. [Google Scholar] [CrossRef]
- Yang, L.; Ma, B.; Ahmadian, M.; Li, H.; Vick, B. Pressure distribution of a multidisc clutch suffering frictionally induced thermal load. Tribol. Trans. 2016, 59, 983–992. [Google Scholar] [CrossRef]
- Yu, L.; Ma, B.; Li, H.; Liu, J.; Li, M. Numerical and experimental studies of a wet multidisc clutch on temperature and stress fields excited by the concentrated load. Tribol. Trans. 2019, 62, 8–21. [Google Scholar] [CrossRef]
- Li, L.; Li, H.; Wang, L. Numerical analysis of dynamic characteristics of wet friction temperature fields. Adv. Mech. Eng. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Meng, Q.; Tian, Z.; Zhao, C. Non-uniform contact characteristics of the friction disc during the initial period of a braking process. J. Mech. Sci. Technol. 2018, 32, 1261–1268. [Google Scholar] [CrossRef]
- Bao, H.; Kong, W.; Hou, X.; Zhu, R. Analysis on temperature field of friction pair of aviation friction clutch based on different groove shapes of friction disk. J. Mech. Sci. Technol. 2021, 35, 3735–3742. [Google Scholar] [CrossRef]
- Grzes, P. Maximum temperature of the disc during repeated braking applications. Adv. Mech. Eng. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Bao, J.; Yin, Y.; Lu, L.; Liu, T. Tribological characterization on friction brake in continuous braking. Ind. Lubr. Tribol. 2018, 70, 172–181. [Google Scholar] [CrossRef]
- Yanar, H.; Purcek, G.; Demirtas, M.; Ayar, H.H. Effect of hexagonal boron nitride (h-BN) addition on friction behavior of low-steel composite brake pad material for railway applications. Tribol. Int. 2022, 165, 107274. [Google Scholar] [CrossRef]
- Pisaturo, M.; Senatore, A. Simulation of engagement control in automotive dry-clutch and temperature field analysis through finite element model. Appl. Therm. Eng. 2016, 93, 958–966. [Google Scholar] [CrossRef]
- Zhao, E.H.; Ma, B.; Li, H.Y. Numerical and experimental studies on tribological behaviors of Cu-based friction pairs from hydrodynamic to boundary lubrication. Tribol. Trans. 2018, 61, 347–356. [Google Scholar] [CrossRef]
- Yu, L.; Ma, B.; Chen, M.; Li, H.; Zhang, H.; Liu, J. Thermodynamic differences of different friction pairs in a multidisc clutch caused by spline friction: Numerical simulation and experimental verification. Tribol. Trans. 2019, 62, 724–736. [Google Scholar] [CrossRef]
- Zheng, L.; Ma, B.; Chen, M.; Yu, L.; Wang, Q. Influence of the lubrication oil temperature on the disengaging dynamic characteristics of a Cu-based wet multi-disc clutch. Appl. Sci. 2021, 11, 11299. [Google Scholar] [CrossRef]
- Lankarani, H.M.; Nikravesh, P.E. A contact force model with hysteresis damping for impact analysis of multibody systems. J. Mech. Des. 1990, 112, 369–376. [Google Scholar] [CrossRef]










| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Ared | 0.65 | m0/(kg) | 1 | β/(m) | 8 × 10−4 |
| cs/(N·s/m) | 0.0466 | m1/(kg) | 0.25 | σ/(m) | 8.4 × 10−6 |
| cst/(J/(kg·°C)) | 487 | m2/(kg) | 0.32 | Ψ/(m2) | 2 × 10−12 |
| cfc/(J/(kg·°C)) | 536 | MR/(N·m) | 5 × 10−4 | μspline | 0.1 |
| cl/(J/(kg·°C)) | 2231 | N/(m−2) | 7 × 107 | λst/(W/(m·°C)) | 45.9 |
| dm/(m) | 5 × 10−4 | Ri/(m) | 0.06 | λfc/(W/(m·°C)) | 9.3 |
| /(Pa) | 4.84 × 109 | Ro/(m) | 0.073 | λl/(W/(m·°C)) | 0.3 |
| Hfd/(m) | 2.5 × 10−3 | Toil/(°C) | 100 | ρst/(kg/m3) | 7800 |
| Hsd/(m) | 2 × 10−3 | η/(Pa·s) | 0.0121 | ρfc/(kg/m3) | 5500 |
| If2/(kg·m2) | 0.248 | ε/(m) | 5 × 10−4 | ρl/(kg/m3) | 875 |
| Toil/(°C) | 60 | 80 | 100 | 120 | 140 |
|---|---|---|---|---|---|
| δ0/(mm) | 0.0024 | 0.0025 | 0.0026 | 0.0027 | 0.0028 |
| δ1/(mm) | 3.3873 | 3.3664 | 3.3474 | 3.3004 | 3.2221 |
| δ2/(mm) | 0.3252 | 0.3331 | 0.3392 | 0.3570 | 0.3845 |
| δ3/(mm) | 0.2488 | 0.2543 | 0.2585 | 0.2695 | 0.2884 |
| δ4/(mm) | 0.1996 | 0.2030 | 0.2064 | 0.2139 | 0.2271 |
| δ5/(mm) | 0.1774 | 0.1799 | 0.1827 | 0.1888 | 0.1993 |
| δ6/(mm) | 0.1571 | 0.1585 | 0.1606 | 0.1652 | 0.1730 |
| δ7/(mm) | 0.0024 | 0.0025 | 0.0026 | 0.0027 | 0.0028 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Ma, B.; Chen, M.; Yu, L.; Wang, Q.; Xue, J. Study on the Temperature Rise Characteristics of Successive Clutch Shifting Considering the Disengaged Friction Pair Gaps. Machines 2022, 10, 576. https://doi.org/10.3390/machines10070576
Zheng L, Ma B, Chen M, Yu L, Wang Q, Xue J. Study on the Temperature Rise Characteristics of Successive Clutch Shifting Considering the Disengaged Friction Pair Gaps. Machines. 2022; 10(7):576. https://doi.org/10.3390/machines10070576
Chicago/Turabian StyleZheng, Liangjie, Biao Ma, Man Chen, Liang Yu, Qian Wang, and Jiaqi Xue. 2022. "Study on the Temperature Rise Characteristics of Successive Clutch Shifting Considering the Disengaged Friction Pair Gaps" Machines 10, no. 7: 576. https://doi.org/10.3390/machines10070576
APA StyleZheng, L., Ma, B., Chen, M., Yu, L., Wang, Q., & Xue, J. (2022). Study on the Temperature Rise Characteristics of Successive Clutch Shifting Considering the Disengaged Friction Pair Gaps. Machines, 10(7), 576. https://doi.org/10.3390/machines10070576