Proton Bridging in Catalysis by and Inhibition of Serine Proteases of the Blood Cascade System
Abstract
:1. Introduction
2. Kinetic Probes of Catalysis by Serine Proteases
2.1. The Double Displacement Mechanism of Serine Protease Catalysis of Peptide/Protein Hydrolysis
2.2. The Catalytic Site of Serine Proteases
2.3. Solvent Isotope Effects and Proton Inventories

3. Structural Probes of Reaction Intermediates
3.1. High Resolution, Low-Field Nuclear Magnetic Resonance (1H NMR) Signals at Catalytic Bridges and in Binding Interactions
3.2. Computational Studies: Molecular Dynamics
4. Basic Characteristics of the Enzymes of Bold Clotting Supporting the Catalytic Function
4.1. The Catalytic Mechanism of α-Thrombin and the Role of Water Networks
4.2. Thrombin Inhibition by the Hirudin Family
5. The Occurrence of Short Hydrogen Bonds (SHBs) in Catalysis by and Inhibition of Blood-Clotting Enzymes
5.1. Probing the Dependence of Proton Sharing at the Transition States on Subsite Binding of Substrates
5.2. Proton Inventories for the Hydrolysis of Natural Substrates Catalyzed by Thrombin and FXa
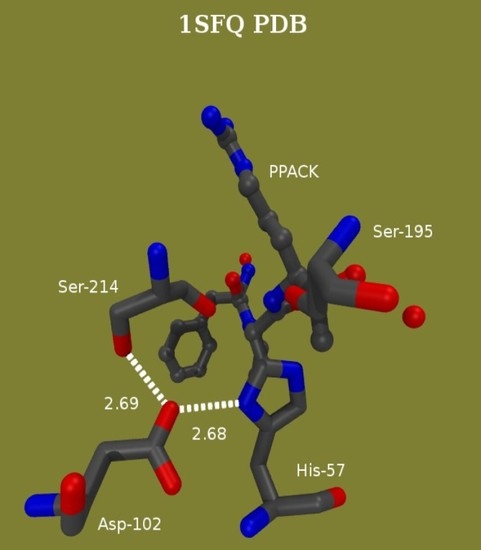
5.3. Probing the Proton Bridges in Covalent and Non-Covalent Adducts of Thrombin
5.3.1. Kinetic Characterization of Thrombin Inhibition with Covalent Modifiers
E + I
 EI
EI  EI*
EI*  EI**
EI**
5.3.2. SHB in Covalent Adducts Detected by Low-Field 1H NMR
5.3.3. A 1 ns Molecular Dynamics (MD) Simulation and Preliminary Quantum Mechanical/Molecular Mechanical (QM/MM) Calculation
5.3.4. SHBs in Non-Covalent Adducts of Thrombin
5.3.5. Sequence Specificity of the 1H NMR Resonances in Thrombin-Hirudin Complexes
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
Appendix A. Experimental Methods Employed in the Investigations of Short Proton Bridges in the Blood-Clotting Enzymes
Appendix A.1. Materials Used
Appendix A.2. Solvent Isotope Effect and Proton Inventory Measurements and Techniques
Appendix A.3. Experiments for Fibrinogen Activation
Appendix A.4. Experiments for Protein C (PC) Activation
Appendix A.5. Experiments for the Inactivation of Thrombin by Active-Site Inhibitors
E + I
 EI
EI  EI*
EI*
Appendix A.6. Prothrombin Activation Catalyzed by Human FXa
Appendix A.7. Low-Field 1H NMR Protocol
References
- Schowen, R.L. Catalytic Power and Transition-State Stabilization. In Transition States of Biochemical Proceses; Gandour, R.D., Schowen, R.L., Eds.; Plenum: New York, NY, USA, 1978; pp. 77–114. [Google Scholar]
- Schowen, R.L. Structural and Energetic Aspects of Protolytic Catalysis by Enzymes: Charge-Relay Catalysis in the Function of Serine Proteases. In Mechanistic Principles of Enzyme Activity; Liebman, J.F., Greenberg, A., Eds.; VCH Publishers: New York, NY, USA, 1988; Volume 9, pp. 119–168. [Google Scholar]
- Fersht, A. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding; W.H. Freeman and Company: New York, NY, USA, 1999. [Google Scholar]
- Schowen, K.B.; Schowen, R.L. Solvent isotope effects on enzyme systems. Methods Enzymol. 1982, 87, 551–606. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, F.J.; Schowen, R.L. Mechanistic Deductions from Solvent Isotope Effects. In Isotopes in Organic Chemistry; Buncel, E., Lee, C.C., Eds.; Elsevier: Amsterdam, The Netherlands, 1987; Volume 7, pp. 1–60. [Google Scholar]
- Bachovchin, W.W. Confirmation of the assignment of the low-field proton resonance of serine proteases by using specifically nitrogen-15 labeled enzyme. Proc. Natl. Acad. Sci. USA 1985, 82, 7948–7951. [Google Scholar] [CrossRef] [Green Version]
- Frey, P.; Whitt, S.; Tobin, J. A low-barrier hydrogen bond in the catalytic triad of serine proteases. Science 1994, 264, 1927–1930. [Google Scholar] [CrossRef] [PubMed]
- Cleland, W.; Kreevoy, M. Low-barrier hydrogen bonds and enzymic catalysis. Science 1994, 264, 1887–1890. [Google Scholar] [CrossRef]
- Perrin, C.L.; Nielson, J.B. “Strong” hydrogen bonds in chemistry and biology. Annu. Rev. Phys. Chem. 1997, 48, 511–544. [Google Scholar] [CrossRef]
- Cassidy, C.S.; Lin, J.; Frey, P.A. A New Concept for the Mechanism of Action of Chymotrypsin: The Role of the Low-Barrier Hydrogen Bond. Biochemistry 1997, 36, 4576–4584. [Google Scholar] [CrossRef]
- Ash, E.L.; Sudmeier, J.L.; De Fabo, E.C.; Bachovchin, W.W. A low-barrier hydrogen bond in the catalytic triad of serine proteases? Theory versus experiment. Science 1997, 278, 1128–1132. [Google Scholar] [CrossRef] [PubMed]
- Markley, J.L.; Westler, W.M. Protonation-state dependence of hydrogen bond strengths and exchange rates in a serine protease catalytic triad: Bovine chymotrypsinogen A. Biochemistry 1996, 35, 11092–11097. [Google Scholar] [CrossRef]
- Bachovchin, W.W. Review: Contributions of NMR spectroscopy to the study of hydrogen bonds in serine protease active sites. Magn. Reson. Chem. 2001, 39, S199–S213. [Google Scholar] [CrossRef]
- Mildvan, A.; Massiah, M.; Harris, T.; Marks, G.; Harrison, D.; Viragh, C.; Reddy, P.; Kovach, I. Short, strong hydrogen bonds on enzymes: NMR and mechanistic studies. J. Mol. Struct. 2002, 615, 163–175. [Google Scholar] [CrossRef]
- Kohen, A. Current Issues in Enzymatic Hydrogen Transfer from Carbon: Tunneling and Coupled Motion from Kinetic Isotope Effect Studies. In Hydrogen-Transfer Reactions; Hynes, J.T., Klinman, J.P., Limbach, H.-H., Schowen, R.L., Eds.; WILEY-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2007; Volume 4, pp. 1311–1340. [Google Scholar]
- Garcia-Viloca, M.; Gonzalez-Lafont, A.; Lluch, J.M. On pKa Matching as a Requirement to Form a Low-Barrier Hydrogen Bond. A Theoretical Study in Gas Phase. J. Phys. Chem. 1997, 101, 3880–3886. [Google Scholar] [CrossRef]
- Polgar, L. Mechanisms in Protease Action; CRC Press Inc.: Boca Raton, FL, USA, 1990. [Google Scholar]
- Hedstrom, L. Serine protease mechanism and specificity. Chem. Rev. 2002, 102, 4501–4524. [Google Scholar] [CrossRef]
- Schowen, K.; Limbach, H.-H.; Denisov, G.; Schowen, R. Hydrogen bonds and proton transfer in general-catalytic transition-state stabilization in enzyme catalysis. Biochim. Biophys. Acta (BBA) Bioenergy 2000, 1458, 43–62. [Google Scholar] [CrossRef] [Green Version]
- Enyedy, E.J.; Kovach, I.M. Proton inventory studies of α-thrombin-catalyzed reactions of substrates with selected P and P’ sites. J. Am. Chem. Soc. 2004, 126, 6017–6024. [Google Scholar] [CrossRef]
- Zhang, D.; Kovach, I.M. Full and partial deuterium solvent isotope effect studies of α-thrombin-catalyzed reactions of natural substrates. J. Am. Chem. Soc. 2005, 127, 3760–3766. [Google Scholar] [CrossRef]
- Zhang, D.; Kovach, I.M. Deuterium solvent isotope effect and proton-inventory studies of factor Xa-catalyzed reactions. Biochemistry 2006, 45, 14175–14182. [Google Scholar] [CrossRef] [Green Version]
- Kovach, I.M.; Kelley, P.; Eddy, C.; Jordan, F.; Baykal, A. Proton bridging in the interactions of thrombin with small inhibitors. Biochemistry 2009, 48, 7296–7304. [Google Scholar] [CrossRef]
- Viragh, C.; Harris, T.K.; Reddy, P.M.; Massiah, M.A.; Mildvan, A.S.; Kovach, I.M. NMR evidence for a short, strong hydrogen bond at the active site of a cholinesterase. Biochemistry 2000, 39, 16200–16205. [Google Scholar] [CrossRef] [PubMed]
- Massiah, M.A.; Viragh, C.; Reddy, P.M.; Kovach, I.M.; Johnson, J.; Rosenberry, T.L.; Mildvan, A.S. Short, strong hydrogen bonds at the active site of human acetylcholinesterase: Proton NMR studies. Biochemistry 2001, 40, 5682–5690. [Google Scholar] [CrossRef]
- Kovach, I.M.; Kakalis, L.; Jordan, F.; Zhang, D. Proton bridging in the interactions of thrombin with hirudin and its mimics. Biochemistry 2013, 52, 2472–2481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Enyedy, E.J.; Kovach, I.M. Modulation of the activity of human α-thrombin with phosphonate ester inhibitors. Bioorg. Med. Chem. 1997, 5, 1531–1541. [Google Scholar] [CrossRef]
- Zhao, Q.; Kovach, I.M.; Bencsura, A.; Papathanassiu, A. Enantioselective and reversible inhibition of trypsin and α chymotrypsin by phosphonate esters. Biochemistry 1994, 33, 8128–8138. [Google Scholar] [CrossRef]
- Das, J.; Kimball, S.D. Thrombin active site inhibitors. Bioorg. Med. Chem. 1995, 3, 999–1007. [Google Scholar] [CrossRef]
- Schulman, S.; Furie, B. The molecular basis of blood coagulation. Cell 2014, 53, 505–518. [Google Scholar] [CrossRef]
- Davie, E.W.; Fujikawa, K.; Kisiel, W. The coagulation cascade: Initiation, maintenance, and regulation. Biochemistry 1991, 30, 10363–10370. [Google Scholar] [CrossRef]
- Berliner, L.J. Thrombin: Structure and Function; Plenum Press: New York, NY, USA, 1992. [Google Scholar]
- Mann, K.G.; Lorand, L. Introduction: Blood coagulation. Methods Enzymol. 1993, 222, 1–10. [Google Scholar] [CrossRef]
- Patthy, L. Modular design of proteases of coagulation, fibrinolysis, and complement activation: Implications for protein engineering and structure-function studies. Methods Enzymol. 1993, 222, 10–21. [Google Scholar] [CrossRef]
- Hopfner, K.P.; Ayala, Y.; Szewczuk, Z.; Konishi, Y.; Di Cera, E. Chemical compensation in macromolecular bridge-binding to thrombin. Biochemistry 1993, 32, 2947–2953. [Google Scholar] [CrossRef]
- Picozzi, M.; Landolfi, R.; Cristofaro, R. Effects of protons on the thrombin-fibrinogen interaction. Eur. J. Biochem. 1994, 219, 1013–1021. [Google Scholar] [CrossRef] [PubMed]
- Stone, S.R.; Hofsteenge, J. Kinetics of the inhibition of thrombin by hirudin. Biochemistry 1986, 25, 4622–4628. [Google Scholar] [CrossRef] [PubMed]
- Stone, S.R.; Braun, P.J.; Hofsteenge, J. Identification of regions of alpha-thrombin involved in its interaction with hirudin. Biochemistry 1987, 26, 4617–4624. [Google Scholar] [CrossRef]
- Braun, P.J.; Dennis, S.; Hofsteenge, J.; Stone, S.R. Use of site-directed mutagenesis to investigate the basis for the specificity of hirudin. Biochemistry 1988, 27, 6517–6522. [Google Scholar] [CrossRef]
- Stone, S.R.; Dennis, S.; Hofsteenge, J. Quantitative evaluation of the contribution of ionic interactions to the formation of the thrombin-hirudin complex. Biochemistry 1989, 28, 6857–6863. [Google Scholar] [CrossRef]
- Dennis, S.; Wallace, A.; Hofsteenge, J.; Stone, S.R. Use of fragments of hirudin to investigate thrombin-hirudin interaction. Eur. J. Biochem. 1990, 188, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Betz, A.; Hofsteenge, J.; Stone, S.R. Ionic interactions in the formation of the thrombin-hirudin complex. Biochem. J. 1991, 275, 801–803. [Google Scholar] [CrossRef] [Green Version]
- Stone, S.R.; Hofsteenge, J. Basis for the reduced affinity of bT- and gT-thrombin for hirudin. Biochemistry 1991, 30, 3950–3955. [Google Scholar] [CrossRef]
- Karshikov, A.; Bode, W.; Tulinsky, A.; Stone, S.R. Electrostatic interactions in the association of proteins: An analysis of the thrombin-hirudin complex. Protein Sci. 1992, 1, 727–735. [Google Scholar] [CrossRef] [Green Version]
- Myles, T.; Le Bonniec, B.F.; Betz, A.; Stone, S.R. Electronic steering and ionic tethering in the formation of thrombin-hirudin complexes: The role of the thrombin anion-binding Exosite-I. Biochemistry 2001, 40, 4972–4979. [Google Scholar] [CrossRef]
- Stone, S.R.; Betz, A.; Parry, M.A.; Jackman, M.P.; Hofsteenge, J. Molecular basis for the inhibition of thrombin by hirudin. Adv. Exp. Med. Biol. 1993, 340, 35–49. [Google Scholar] [PubMed]
- Huntington, J.A. Natural inhibitors of thrombin. Thromb. Haemost. 2014, 111, 583–589. [Google Scholar] [CrossRef] [Green Version]
- Lombardi, A.; Nastri, F.; Morte, R.D.; Rossi, A.; De Rosa, A.; Staiano, N.; Pedone, C.; Pavone, V. Rational design of true hirudin mimetics: Synthesis and characterization of multisite-directed α-thrombin inhibitors1. J. Med. Chem. 1996, 39, 2008–2017. [Google Scholar] [CrossRef]
- Lombardi, A.; De Simone, G.; Galdiero, S.; Staiano, N.; Nastri, F.; Pavone, V. From natural to synthetic multisite thrombin inhibitors. Biopolymers 1999, 51, 19–39. [Google Scholar] [CrossRef]
- Vijayalakshmi, J.; Padmanabhan, K.P.; Tulinsky, A.; Mann, K.G. The isomorphous structures of prethrombin2, hirugen-, and PPACK-thrombin: Changes accompanying activation and exosite binding to thrombin. Protein Sci. 1994, 3, 2254–2271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Yan, X.; Mo, W.; Song, H.; Dai, L. Spectral assignments and reference data: H NMR assignment and secondary structure of recombinant RGD-hirudin. Magn. Reson. Chem. 2005, 43, 956–961. [Google Scholar] [CrossRef]
- Friedrich, R.; Steinmetzer, T.; Huber, R.; Sturzebecher, J.; Bode, W. The methyl group of Nα(Me)Arg-containing peptides disturbs the active-site geometry of thrombin impairing efficient cleavage. J. Mol. Biol. 2002, 316, 869–874. [Google Scholar] [CrossRef] [PubMed]
- De Simone, G.; Lombardi, A.; Galdiero, S.; Nastri, F.; Morte, R.D.; Staiano, N.; Pedone, C.; Bolognesi, M.; Pavone, V. Hirunorms are true hirudin mimetics. The crystal strcture of human a-thrombin-hirunorm V complex. Protein Sci. 1998, 7, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Lombardi, A.; De Simone, G.; Nastri, F.; Galdiero, S.; Pedone, C.; Pavone, V.; Della Morte, R.; Staiano, N.; Bolognesi, M. The crystal structure of α-thrombin-hirunorm IV complex reveals a novel specificity site recognition mode. Protein Sci. 2008, 8, 91–95. [Google Scholar] [CrossRef]
- Liu, C.C.; Brustad, E.; Liu, W.; Schultz, P.G. Crystal structure of a biosynthetic Sulfo-hirudin complexed to thrombin. J. Am. Chem. Soc. 2007, 129, 10648–10649. [Google Scholar] [CrossRef] [Green Version]
- Hirohara, H.; Bender, M.L.; Stark, R.S. Acylation of -chymotrypsin by oxygen and sulfur esters of specific substrates: Kinetic evidence for a tetrahedral intermediate. Proc. Natl. Acad. Sci. USA 1974, 71, 1643–1647. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miller, C.G.; Bender, M.L. Direct observation of an acyl-enzyme intermediate in the alpha-chymotrypsin-catalyzed hydrolysis of a specific substrate at neutral pH. J. Am. Chem. Soc. 1968, 90, 6850–6852. [Google Scholar] [CrossRef]
- Michaelis, L.; Menten, M.L. Die kinetik der invertinwirkung. Biochem. Z. 1913, 49, 333–369. [Google Scholar]
- Quinn, D.M.; Sutton, L.D. Theoretical Basis and Mechanistic Utility of Solvent Isotope Effects. In Enzyme Mechanism from Isotope Effects; Cook, P.F., Ed.; CRC Press: Boston, MA, USA, 1991; pp. 73–126. [Google Scholar]
- Elrod, J.P.; Hogg, J.L.; Quinn, D.M.; Venkatasubban, K.S.; Schowen, R.L. Protonic reorganization and substrate structure in catalysis by serine proteases. J. Am. Chem. Soc. 1980, 102, 3917–3922. [Google Scholar] [CrossRef]
- Stein, R.L.; Elrod, J.P.; Schowen, R.L. Correlative variations in enzyme-derived and substrate-derived structures of catalytic transition states. Implications for the catalytic strategy of acyl-transfer enzymes. J. Am. Chem. Soc. 1983, 105, 2446–2452. [Google Scholar] [CrossRef]
- Stein, R.L. Catalysis by human leukocyte elastase: Substrate structural dependence of rate-limiting protolytic catalysis and operation of the charge relay system. J. Am. Chem. Soc. 1983, 105, 5111–5116. [Google Scholar] [CrossRef]
- Stein, R.L.; Strimpler, A.M.; Hori, H.; Powers, J.C. Catalysis by human leukocyte elastase: Mechanistic insights into specificity requirements. Biochemistry 1987, 26, 1301–1305. [Google Scholar] [CrossRef]
- Stein, R.L.; Trainor, D.A. Mechanism of inactivation of human leukocyte elastase by a chlorromethyl ketone: Kinetic and solvent isotope effect studies. Biochemistry 1986, 25, 5414–5419. [Google Scholar] [CrossRef]
- Venkatasubban, K.S.; Schowen, R.L. The proton inventory technique. CRC Crit. Rev. Biochem. 1985, 17, 1–44. [Google Scholar]
- Scholten, J.D.; Hogg, J.L.; Raushel, F.M. Methyl chymotrypsin catalyzed hydrolysis of specific substrate esters indicate multiple proton catalysis is possible with a modified charge relay triad. J. Am. Chem. Soc. 1988, 110, 8246–8247. [Google Scholar] [CrossRef]
- Chang, T.K.; Chiang, Y.; Guo, H.-X.; Kresge, A.J.; Mathew, L.; Powell, M.F.; Wells, J.A. Solvent isotope effects in H2O-D2O mixtures (proton inventories) on serine-protease-catalyzed hydrolysis reactions. Influence of oxyanion hole interactions and medium effects. J. Am. Chem. Soc. 1996, 118, 8802–8807. [Google Scholar] [CrossRef]
- Tobin, J.B.; Whitt, S.A.; Cassidy, C.S.; Frey, P.A. Low-barrier hydrogen bonding in molecular complexes analogous to histidine and aspartate in the catalytic triad of serine proteases. Biochemistry 1995, 34, 6919–6924. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Cassidy, C.S.; Frey, P.A. Correlations of the basicity of His 57 with transition state analogue binding, substrate reactivity, and the strength of the low-barrier hydrogen bond in chymotrypsin. Biochemistry 1998, 37, 11940–11948. [Google Scholar] [CrossRef]
- Lin, J.; Westler, W.M.; Cleland, W.W.; Markley, J.L.; Frey, P.A. Fractionation factors and activation energies for exchange of the low barrier hydrogen bonding proton in peptidyl trifluoromethyl ketone complexes of chymotrypsin. Proc. Natl. Acad. Sci. USA 1998, 95, 14664–14668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, J.; Frey, P.A. Strong hydrogen bonds in aqueous and aqueous—Acetone solutions of dicarboxylic acids: Activation energies for exchange and deuterium fractionation factors. J. Am. Chem. Soc. 2000, 122, 11258–11259. [Google Scholar] [CrossRef]
- Halkides, C.J.; Wu, Y.Q.; Murray, C.J. A low-barrier hydrogen bond in subtilisin: 1H and15N NMR studies with peptidyl trifluoromethyl ketones. Biochemistry 1996, 35, 15941–15948. [Google Scholar] [CrossRef] [PubMed]
- Kahyaoglu, A.; Haghjoo, K.; Guo, F.; Jordan, F.; Kettner, C.; Felföldi, F.; Polgár, L. Low barrier hydrogen bond is absent in the catalytic triads in the ground state but is present in a transition-state complex in the prolyl oligopeptidase family of serine proteases. J. Biol. Chem. 1997, 272, 25547–25554. [Google Scholar] [CrossRef] [Green Version]
- Bao, D.; Huskey, P.W.; Kettner, C.A.; Jordan, F. Hydrogen bonding to active-site histidine in peptidyl Botonic acid inhibitor complexes of chymotrypsin and subtilisin: Proton magnetic resonance assignments and H/D fractionation. J. Am. Chem. Soc. 1999, 121, 4684–4689. [Google Scholar] [CrossRef]
- Schellenberger, V.; Turck, C.W.; Hedstrom, L.; Rutter, W.J. Mapping the S’ subsites of serine proteases using acyl transfer to mixtures of peptide nucleophiles. Biochemistry 1993, 32, 4349–4353. [Google Scholar] [CrossRef]
- Schellenberger, V.; Turck, C.W.; Rutter, W.J. Role of the S’ subsites in serine protease catalysis. Active-site mapping of rat Chymotrypsin, rat trypsin, alpha-lytic protease, and cercarial protease from Schistosoma mansoni. Biochemistry 1994, 33, 4251–4257. [Google Scholar] [CrossRef]
- Le Bonniec, B.F.; Myles, T.; Johnson, T.; Knight, C.G.; Tapparelli, C.; Stone, S.R. Characterization of the P2’ and P3’ specificities of thrombin using fluorescence-quenched substrates and mapping of the subsites by mutagenesis. Biochemistry 1996, 35, 7114–7122. [Google Scholar] [CrossRef]
- Dai, Y.; Hedstrom, L.; Abeles, R.H. Inactivation of cysteine proteases by (acyloxy)methyl ketones using S’-P’ interactions. Biochemistry 2000, 39, 6498–6502. [Google Scholar] [CrossRef] [PubMed]
- Mildvan, A.S.; Harris, T.K.; Abeygunawardana, C. Nuclear magnetic resonance methods for the detection and study of low-barrier hydrogen bonds on enzymes. Methods Enzymol. 1999, 308, 219–245. [Google Scholar]
- Harris, T.K.; Mildvan, A.S. High-precision measurement of hydrogen bond lengths in proteins by nuclear magnetic resonance methods. Protein Struct. Funct. Genet. 1999, 35, 275–282. [Google Scholar] [CrossRef]
- Harris, T.; Zhao, Q.; Mildvan, A. NMR studies of strong hydrogen bonds in enzymes and in a model compound. J. Mol. Struct. 2000, 552, 97–109. [Google Scholar] [CrossRef]
- Schenier, S.; Karr, T. The nonexistence of specially stabilized hydrogen bonds in enzymes. J. Am. Chem. Soc. 1995, 117, 6970–6975. [Google Scholar] [CrossRef]
- Perrin, C.L. Are short, low-barrier hydrogen bonds unusually strong? Acc. Chem. Res. 2010, 43, 1550–1557. [Google Scholar] [CrossRef]
- Warshel, A.; Papzyan, A.; Kollman, P.A. On low-barrier hydrogen bonds and enzyme catalysts. Science 1995, 269, 104. [Google Scholar] [CrossRef] [Green Version]
- Hibbert, F.; Emsley, J. Hydrogen bonding and chemical reactivity. Adv. Phys. Org. Chem. 1990, 26, 255–379. [Google Scholar] [CrossRef]
- De Filippis, V.; Colombo, G.; Russo, I.; Spadari, B.; Fontana, A. Probing the hirudin-thrombin interaction by incorporation of nonbonded amino acids and molecular dynamics simulation. Biochemistry 2002, 41, 13556–13569. [Google Scholar] [CrossRef]
- Pineda, A.O.; Carrell, C.J.; Bush, L.A.; Prasad, S.; Caccia, S.; Chen, Z.-W.; Mathews, F.S.; Di Cera, E. Molecular dissection of Na+ binding to thrombin. J. Biol. Chem. 2004, 279, 31842–31853. [Google Scholar] [CrossRef] [Green Version]
- Di Cera, E. Thrombin. Mol. Asp. Med. 2008, 29, 203–254. [Google Scholar] [CrossRef] [PubMed]
- Huntington, J.A. How Na+ activates thrombin—A review of the functional and structural data. Biol. Chem. 2008, 389, 1025–1035. [Google Scholar] [CrossRef]
- Fuglestad, B.; Gasper, G.M.; Tonelli, M.; McCammon, J.A.; Phineus, R.; Markwick, L.; Komives, E.A. The dynamic structure of thrombin in solution. Biophys. J. 2012, 103, 79–88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, J.; Salisbury, R.F., Jr. Molecular dynamics simulations of aptamer-binding reveal generalized allostery in thrombin. Parasitol. Res. Thromb. Haemost. 2014, 111, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Phineus, R.L.; Markwick, L.; Riley, B.; Peacock, L.; Komives, E.A. Accurate prediction of amide exchange in the fast limit reveals thrombin allostery. Biophys. J. 2019, 116, 49–56. [Google Scholar]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Enyedy, I.; Bencsura, A.; Kovach, I.M. Interactions in tetravalent and pentavalent phosphonate esters at the active site of serine enzymes. Phosphorus Sulfur Silicon 1996, 109–110, 249–252. [Google Scholar]
- Bencsura, A.; Enyedy, I.; Kovach, I.M. Probing the active site of acetylcholinesterase by molecular dynamics of its phosphonate ester adducts. J. Am. Chem. Soc. 1996, 118, 8531–8541. [Google Scholar] [CrossRef]
- Bencsura, A.; Enyedy, I.; Kovach, I.M. Origins and diversity of the aging reaction in phosphonate adducts of serine hydrolase enzymes: What characteristics of the active site do they probe? Biochemistry 1995, 34, 8989–8999. [Google Scholar] [CrossRef] [PubMed]
- DiBella, E.E.; Scheraga, H.A. The role of the insertion loop around tryptophan 148 in the activity of thrombin. Biochemistry 1996, 35, 4427–4433. [Google Scholar] [CrossRef]
- Le Bonniec, B.F.; Esmon, C.T. Glu-192—Gln substitution in thrombin mimics the catalytic switch induced by thrombomodulin. Proc. Natl. Acad. Sci. USA 1991, 88, 7371–7375. [Google Scholar] [CrossRef] [Green Version]
- Le Bonniec, B.F.; Guinto, E.R.; Stone, S.R. Identification of thrombin residues that modulate its interactions with antithrombin III and 1 antitrypsin. Biochemistry 1995, 34, 12241–12248. [Google Scholar] [CrossRef]
- Bode, W.; Turk, D.; Karshikov, A. The refined 1.9-Å X-ray crystal structure of d-Phe-Pro-Arg chloromethylketone-inhibited human α -thrombin: Structure analysis, overall structure, electrostatic properties, detailed active-site geometry, and structure-function relationships. Protein Sci. 1992, 1, 426–471. [Google Scholar] [CrossRef]
- Bode, W.; Mayr, I.; Baumann, U.; Huber, R.; Stone, S.R.; Hofsteenge, J. The refined 1.9 Å crystal structure of human α thrombin: Interaction with D Phe Pro Arg Chloromethylketone and significance of the Tyr Pro Pro Trp insertion segment. EMBO J. 1989, 8, 3467–3475. [Google Scholar] [CrossRef] [PubMed]
- Bode, W. Structure and interaction modes of thrombin. Blood Cells Mol. Dis. 2006, 36, 122–130. [Google Scholar] [CrossRef] [PubMed]
- Jankun, E.S.; Carperos, V.; Ravichandran, K.G.; Tulinsky, A.; Westbrook, M.; Maraganore, J.M. Structure of the Hirugen and Hirulog 1 complexes of α Thrombin. J. Mol. Biol. 1991, 221, 1379–1393. [Google Scholar] [CrossRef]
- Boskovic, D.S.; Bajzar, L.S.; Nesheim, M.E. Channeling during prothrombin activation. J. Biol. Chem. 2001, 276, 28686–28693. [Google Scholar] [CrossRef] [Green Version]
- Padmanabhan, K.; Padmanabhan, K.P.; Tulinsky, A.; Park, C.H.; Bode, W.; Huber, R.; Blankenship, D.T.; Cardin, A.D.; Kisiel, W. Structure of human Des(1 45) factor Xa at 2.2 Å resolution. J. Mol. Biol. 1993, 232, 947–966. [Google Scholar] [CrossRef] [PubMed]
- Guinto, E.; Ye, J.; Le Bonniec, B.; Esmon, C. Glu192–>Gln substitution in thrombin yields an enzyme that is effectively inhibited by bovine pancreatic trypsin inhibitor and tissue factor pathway inhibitor. J. Biol. Chem. 1994, 269, 18395–18400. [Google Scholar] [CrossRef]
- Rezaie, A.R.; Esmon, C.T. Contribution of residue 192 in factor Xa to enzyme specificity and function. J. Biol. Chem. 1995, 270, 16176–16181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rezaie, A.; Neuenschwander, P.; Morrissey, J.; Esmon, C. Analysis of the functions of the first epidermal growth factor-like domain of factor X. J. Biol. Chem. 1993, 268, 8176–8180. [Google Scholar] [CrossRef]
- Di Cera, E.; Dang, Q.D.; Ayala, Y.; Vindigni, A. Linkage at steady state: Allosteric transitions of thrombin. Methods Enzymol. 1995, 259, 127–144. [Google Scholar] [CrossRef] [PubMed]
- Di Cera, E.; Hopfner, K.; Dang, Q. Theory of allosteric effects in serine proteases. Biophys. J. 1996, 70, 174–181. [Google Scholar] [CrossRef] [Green Version]
- Dang, O.D.; Vindigni, A.; Di Cera, E. An allosteric switch controls the procoagulant and anticoagulant activities of thrombin. Proc. Natl. Acad. Sci. USA 1995, 92, 5977–5981. [Google Scholar] [CrossRef] [Green Version]
- Ayala, Y.; Di Cera, E. Molecular recognition by thrombin. Role of the slows—Fast transition, site-specific ion binding energetics and thermodynamic mapping of structural components. J. Mol. Biol. 1994, 235, 733–746. [Google Scholar] [CrossRef]
- Wells, C.M.; Di Cera, E. Thrombin is a Na+ activated enzyme. Biochemistry 1992, 31, 11721–11730. [Google Scholar] [CrossRef] [PubMed]
- Vindigni, A.; Di Cera, E. Release of fibrinopeptides by the slow and fast forms of thrombin. Biochemistry 1996, 35, 4417–4426. [Google Scholar] [CrossRef]
- Di Cera, E.; De Cristofaro, R.; Albright, D.J.; Fenton, J.W. Linkage between proton binding and amidase activity in human alpha-thrombin: Effect of ions and temperature. Biochemistry 1991, 30, 7913–7924. [Google Scholar] [CrossRef]
- Mathur, A.; Schlapkohl, W.A.; Di Cera, E. Thrombin-fibrinogen interaction: pH dependence and effects of the slow fwdarw fast transition. Biochemistry 1993, 32, 7568–7573. [Google Scholar] [CrossRef] [PubMed]
- Lottenberg, R.; Christensen, U.; Jackson, C.M.; Coleman, P.L. Assay of coagulation proteases using peptide chromogenic and fluorogenic substrates. Methods Enzymol. 1981, 28, 341–361. [Google Scholar] [CrossRef]
- Lottenberg, S.R.; Hall, J.A.; Blinder, M.; Binder, E.P.; Jackson, C.M. The action of thrombin on peptide p nitroanilide substrates. Substrate selectivity and examination of hydrolysis under different reaction conditions. Biochim. Biophys. Acta 1983, 742, 539–557. [Google Scholar]
- Kerr, M.A.; Grahn, D.T.; Walsh, K.A.; Neurath, H. Activation of bovine factor X (Stuart factor)—Analogy with pancreatic zymogen-enzyme systems. Biochemistry 1978, 17, 2645–2648. [Google Scholar] [CrossRef]
- Stone, S.R.; Betz, A.; Hofsteenge, J. Mechanistic studies on thrombin catalysis. Biochemistry 1991, 30, 9841–9848. [Google Scholar] [CrossRef] [PubMed]
- Bah, A.; Garvey, L.C.; Ge, J.; Di Cera, E. Rapid kinetics of Na+ binding to thrombin. J. Biol. Chem. 2006, 281, 40049–40056. [Google Scholar] [CrossRef] [Green Version]
- Gianni, S.; Ivarsson, Y.; Bah, A.; Bush-Pelc, L.A.; Di Cera, E. Mechanism of Na+ binding to thrombin resolved by ultra-rapid kinetics. Biophys. Chem. 2007, 131, 111–114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prasad, S.; Wright, K.J.; Roy, D.B.; Bush, L.A.; Cantwell, A.M.; Di Cera, E. Redesigning the monovalent cation specificity of an enzyme. Proc. Natl. Acad. Sci. USA 2003, 100, 13785–13790. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huntington, J.A.; Esmon, C.T. The molecular basis of thrombin allostery revealed by a 1.8 A structure of the “slow” form. Structure 2003, 11, 469–479. [Google Scholar] [CrossRef]
- Huntington, J.A. Thrombin plasticity. Biochim. Biophys. Acta 2012, 1824, 246–252. [Google Scholar] [CrossRef]
- Müller, C.; Haase, M.; Lemke, S.; Hildebrandt, J.-P. Hirudins and hirudin-like factors in Hirudinidae: Implications for function and phylogenetic relationships. Parasitol. Res. 2016, 116, 313–325. [Google Scholar] [CrossRef]
- Sohn, J.H.; Kang, H.A.; Rao, K.J.; Kim, C.H.; Choi, E.S.; Chung, B.H.; Rhee, S.K. Current status of the anticoagulant hirudin: Its biotechnological production and clinical practice. Appl. Microbiol. Biotechnol. 2001, 57, 606–613. [Google Scholar] [CrossRef]
- Rydel, T.; Ravichandran, K.; Tulinsky, A.; Bode, W.; Huber, R.; Roitsch, C.; Fenton, J. The structure of a complex of recombinant hirudin and human alpha-thrombin. Science 1990, 249, 277–280. [Google Scholar] [CrossRef]
- Rydel, T.J.; Tulinsky, A.; Bode, W.; Huber, R. Refined structure of the Hirudin-thrombin complex. J. Mol. Biol. 1991, 221, 583–601. [Google Scholar] [CrossRef]
- Priestle, J.P.; Rahuel, J.; Rink, H.; Tones, M.; Grütter, M.G. Changes in interactions in complexes of hirudin derivatives and human α-thrombin due to different crystal forms. Protein Sci. 1993, 2, 1630–1642. [Google Scholar] [CrossRef] [PubMed]
- Grütter, M.G.; Priestle, J.P.; Rahuel, J.; Grossenbacher, H.; Bode, W.; Hofsteenge, J.; Stone, S.R. Crystal structure of the thrombin-hirudin complex: A novel mode of serine protease inhibition. EMBO J. 1990, 9, 2361–2365. [Google Scholar] [CrossRef]
- Jackman, M.; Parry, M.; Hofsteenge, J.; Stone, S. Intrinsic fluorescence changes and rapid kinetics of the reaction of thrombin with hirudin. J. Biol. Chem. 1992, 267, 15375–15383. [Google Scholar] [CrossRef]
- Egner, U.; Hoyer, G.-A.; Schleuning, W.-D. Rational design of hirulog-type inhibitors of thrombin. J. Comput. Mol. Des. 1994, 8, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Kovach, I.M.; McKay, L. Reversible modulation of serine protease activity by phosphonate esters. Bioorg. Med. Chem. Lett. 1992, 2, 1735. [Google Scholar] [CrossRef]
- Zhang, D.; Kovach, I.M.; Sheehy, J.P. Locating the rate-determining step for three-step hydrolase-catalyzed reactions with DYNAFIT. Biochim. Biophys. Acta Proteins Proteomics 2008, 1784, 827–833. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akhmetshin, R.R. Mechanistic Investigations of Catalysis by Some Hemostatic and Thrombolytic Enzymes. Ph.D. Thesis, The Catholic University of America, Washington, DC, USA, 1998. [Google Scholar]
- Wu, J.R.; Zhou, C.; Majumder, R.; Powers, D.D.; Weinreb, G.; Lentz, B.R. Role of procoagulant lipids in human prothrombin activation. 1. Prothrombin activation by factor X(a) in the absence of factor V(a) and in the absence and presence of membranes. Biochemistry 2002, 41, 935–949. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, M.; Majumder, R.; Weinreb, G.; Wang, J.; Lentz, B.R. Role of procoagulant lipids in human prothrombin activation. 2. Soluble phosphatidylserine upregulates and directs factor X(a) to appropriate peptide bonds in prothrombin. Biochemistry 2002, 41, 950–957. [Google Scholar] [CrossRef] [PubMed]
- Philipp, M.; Bender, M.L. Alpha-chymotrypsin: Is binding the rate-determining step in acylation? Nat. New Biol. 1973, 214, 44–50. [Google Scholar] [CrossRef] [PubMed]
- Bender, M.L.; Wedler, F.C. Phosphate and carbonate ester “aging” reactions with alpha-chymotrypsin. Kinetics and mecha-nism. J. Am. Chem. Soc. 1972, 94, 2101–2109. [Google Scholar] [CrossRef] [PubMed]
- Kovach, I.M. Structure and dynamics of serine hydrolase-organophosphate adducts. J. Enzym. Inhib. 1988, 2, 199–208. [Google Scholar] [CrossRef]
- Kovach, I.M.; McKay, L.; Vander Velde, D. Diastereomeric phosphonate ester adducts of chymotrypsin: 31P-NMR measureents. Chirality 1993, 5, 143–149. [Google Scholar] [CrossRef] [PubMed]
- Bencsura, A.; Enyedy, I.; Viragh, C.; Akhmetshin, R.; Kovach, I.M. Phosphonate Ester Active Site Probes of Acetylcholin-Esterase, Trypsin, and Chymotrypsin. In Enzymes of the Cholinesterase Family; Quinn, D.M., Balasubramanian, A.S., Doctor, B.P., Taylor, P., Eds.; Plenum Press: New York, NY, USA, 1995; pp. 155–162. [Google Scholar]
- Kovach, I.M.; Enyedy, E.J. Active-site-dependent elimination of 4-nitrophenol from 4-nitrophenyl alkylphosphonyl serine protease adducts. J. Am. Chem. Soc. 1998, 120, 258–263. [Google Scholar] [CrossRef]
- Kovach, I.M. Ligand and active-site dependent P-O versus C-O bond cleavage in organophosphorus adducts of serine hydrolases. Phosphorus Sulfur Silicon 1996, 144–146, 537–540. [Google Scholar] [CrossRef]
- Kovach, I.M. Stereochemistry and secondary reactions in the irreversible inhibition of serine hydrolases by organophos-phorus compounds. J. Phys. Org. Chem. 2004, 17, 602–614. [Google Scholar] [CrossRef]
- Bencsura, A.; Kovach, I.M. QM/MM study of short hydrogen bonds in covalently modified α-thrombin. Unpublished work.
- Bachovchin, W.W. 15N NMR spectroscopy of hydrogen-bonding interactions in the active site of serine proteases: Evidence for a moving histidine mechanism. Biochemistry 1986, 25, 7751–7759. [Google Scholar] [CrossRef] [PubMed]
- Vishveshwara, S.; Madhusudhan, M.S.; Maziel, J.V., Jr. Short-strong hydrogen bonds and a low barrier transition state for the proton transfer reaction in RNase A catalysis: A quantum chemical study. Biophys. Chem. 2001, 89, 105–117. [Google Scholar] [CrossRef]
- Kovach, I.M.; Shehey, J.P.; Dole-Nolan, K. Kinetic isotope effects in the inhibition of thrombin with hirudin and its mimics. Unpublished work.
- Song, X.; Mo, W.; Liu, X.; Zhu, L.; Yan, X.; Song, H.; Dai, L. The NMR solution structure of recombinant RGD-hirudin. Biochem. Biophys. Res. Commun. 2007, 360, 103–108. [Google Scholar] [CrossRef] [PubMed]
- Haruyama, H.; Wüthrich, K. Confirmation of recombinant desulfatohirudin in aqueous solution determined by nuclear magnetic resonance. Biochemistry 1989, 28, 4301–4312. [Google Scholar] [CrossRef]
- Folkers, P.J.M.; Clore, G.M.; Driscoll, P.C.; Dodt, J.; Köhler, S.; Gronenborn, A.M. Solution structure of recombinant hirudin and Lys-47-Glu mutant: A nuclear magnetic resonance and hybrid distance geometry-dynamical simulated annealing study. Biochemistry 1989, 28, 2601–2617. [Google Scholar] [CrossRef] [PubMed]
- Rehse, P.H.; Steinmetzer, T.; Li, Y.; Konishi, Y.; Cygler, M. Crystal structure of a peptidyl pyridinium methyl ketone inhibitor with thrombin. Biochemistry 1995, 34, 11537–11544. [Google Scholar] [CrossRef] [PubMed]
- Brandstetter, H.; Turk, D.; Hoeffken, H.W.; Grosse, D.; Stürzebecher, J.; Martin, P.D.; Edwards, B.F.P.; Bode, W. Refined 2.3 Å X-ray crystal structure of bovine thrombin complexes formed with the benzamidine and arginine-based thrombin inhibitors NAPAP, 4-TAPAP and MQPA. J. Mol. Biol. 1992, 226, 1085–1099. [Google Scholar] [CrossRef]
- Bode, W.; Turk, D.; Stürzebecher, J. Geometry of binding of the benzamide- and arginine-based inhibitors Nα-(2-naphthyl-sulphonyl-glycyl)-DL-p-amidinophenylalanyl-piperidine (NAPAP) and (2R,4R)-4-methyl-1-[Nα-(3-methyl-1,2,3,4-tetrahydro-8-quinolinesulphonyl)-L-arginyl]-2-piperidine carboxylic acid (MQPA) to human α-thrombin. X-ray crystallographic determination of the NAPAP-trypsin complex and modeling of NAPAP-thrombin and MQPA-thrombin. Eur. J. Biochem. 1996, 193, 175–182. [Google Scholar]
- Neidhart, D.; Wei, Y.; Cassidy, C.; Lin, J.; Cleland, W.W.; Frey, P.A. Correlation of low-barrier hydrogen bonding and oxyanion binding in transition state analogue complexes of chymotrypsin. Biochemistry 2001, 40, 2439–2447. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Mulichak, A.; Lewis, S.; Shafer, J. Crystal structure of human α-thrombin complexed with hirugen and p-Amidinophenylpyruvate at 1.6 Å resolution. Arch. Biochem. Biophys. 1995, 322, 198–203. [Google Scholar] [CrossRef]
- Shan, S.O.; Loh, S.; Herschlag, D. The energetics of hydrogen bonds in model systems: Implications for enzymatic catalysis. Science 1996, 272, 97–101. [Google Scholar] [CrossRef] [Green Version]
- Shan, S.O.; Hercshlag, D. The change in hydrogen bond strength accompanying charge rearrangement: Implications for enzymatic catalysis. Proc. Natl. Acad. Sci. USA 1996, 93, 14474–14479. [Google Scholar] [CrossRef] [Green Version]
- Fuhrmann, C.N.; Daugherty, M.D.; Agard, D.A. Subangstrom crystallography reveals that short ionic hydrogen bonds, and not a His-Asp low-barrier hydrogen bond, stabilize the transition state in serine protease catalysis. J. Am. Chem. Soc. 2006, 128, 9086–9102. [Google Scholar] [CrossRef]
- Langkilde, A.; Kristensen, S.; Leggio, L.L.; Mølgaard, A.; Jensen, J.H.; Houk, A.R.; Poulsen, J.C.N.; Kauppinen, S.K.; Larsen, S. Short strong hydrogen bonds in proteins: A case study of rhamnogalacturonan acetylesterase. Acta Crystallogr. D-Biol. Crystallogr. 2008, 64, 851–863. [Google Scholar] [CrossRef] [Green Version]
- Rajagopal, S.; Vishveshwara, S. Short hydrogen bonds in proteins. FEBS J. 2005, 272, 1819–1832. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Wang, L. Unraveling the structural and chemical features of biological short hydrogen bonds. Chem. Sci. 2019, 10, 7734–7745. [Google Scholar] [CrossRef] [PubMed]














| Information Obtained | Equation |
|---|---|
| TS1 | kn = kH (1 − n + n ɸ1) |
| TS1, solv. | kn = kH (1 − n + n ɸ1) Sn |
| 2TS1 | kn = kH (1 − n + n ɸ1)2 |
| 2TS1, solv. | kn = kH (1 − n + n ɸ1)2 Sn |
| TS1, TS2 | kn = kH (1 − n + n ɸ1)(1 − n + n ɸ2) |
| ɸ1 | ɸ2 | ɸs | χ2 | |
|---|---|---|---|---|
| kn/kH | ||||
| TS1 | 0.32 ± 0.01 | ---- | ---- | 4.997 |
| TS1, solv. | 0.44 ± 0.05 | ---- | 0.70 ± 0.10 | 2.526 |
| 2TS1 | 0.57 ± 0.01 | 0.57 ± 0.01 | (1.00) | 2.278 |
| 2TS1, solv. | 0.56 ± 0.04 | 0.56 ± 0.04 | 1.04 ±0.15 | 2.514 |
| TS1, TS2 | 0.49 ± 0.15 | 0.66 ± 0.20 | (1.00) | 2.515 |
| (kcat/Km)n/(kcat/Km)H | ||||
| TS1 | 0.73 ± 0.03 | ---- | ---- | 1.335 |
| TS1, solv. | 0.42 ± 0.03 | ---- | 1.65 ± 0.10 | 0.274 |
| 2TS1 | 0.86 ± 0.02 | 0.86 ± 0.02 | (1.00) | 1.514 |
| 2TS1, solv. | 0.55 ± 0.02 | 0.55 ± 0.02 | 2.4 ±0.2 | 0.236 |
| TS1, TS2 | 0.47 ± 0.02 | 1.50 ± 0.06 | (1.00) | 0.222 |
| Residues 1 | DODkcat(SD) | ɸTS; ɸs | DOD(kcat/Km)(SD) | ɸTS; ɸs |
|---|---|---|---|---|
| Thrombin. [20] | ||||
| PR | 3.27(0.13) | 0.38; 0.80 | 2.09(0.04) | 0.38; 1.22 |
| VPR | 3.05(0.05) | 0.44; 0.70 | 1.40(0.05) | 0.42; 1.65 |
| Or | 0.57x 3 | 0.55x2; 2.4 | ||
| SPR-SFQ | 2.24(0.08) | 0.44 | 0.94(0.03) | 0.44; 2.4 2 |
| FPR-SFR | 2.25(0.24) | 0.36x2; 3.1 | 0.81(0.08) | -; 1.2 2 |
| FVR | 2.86(0.06) | 0.63x2 3 | 1.8(0.1) | 0.63x2; 1.2 |
| FPiR | 2.86(0.07) | 0.40x2; 2.0 | 1.0(0.2) | |
| APC [134] | ||||
| IPR | 2.35(0.04) | 0.60x2 3 | 1.80(0.01) | |
| EPR | 2.42(0.01) | 0.60x2 3 | 1.90(0.02) | |
| Plasmin [134] | ||||
| EFK | 3.48(0.02) | 0.60x2 3; 0.7 | 1.83(0.01) | 0.5; 2.1 |
| VFK | 2.32(0.02) | 0.3; 1.3 | 1.56(0.01) | 0.3; 2.5 |
| VLK | 2.76(0.02) | 0.2; 1.4 | 2.52(0.01) | |
| Factor Xa [22] | ||||
| RGR | 3.90(0.05) | 0.60x2 3; 0.72 | 1.88(0.03) | 0.72x2 3 |
| IPR | 2.39(0.53) | 0.66x2 3 | 1.79(0.19) | - |
| Inhibitor | pKa 1 | pKa 2 | ki/Ki, M−1 s−1 max | ki, s−1 pH 7.00 | Ki, M pH 7.00 | ΔH‡ kcal/mol | ΔS‡ cal/mol, K |
|---|---|---|---|---|---|---|---|
| PPACK | 7.3 ± 0.2 | 8.8 ± 0.3 | (2.2 ± 0.3) × 107 | 0.24 ± 0.12 | (2.4 ± 1.3) × 10−8 | 10.6 ± 0.7 | 9 ± 2 |
| Paraoxon | 7.8 ± 0.2 | 9.3 ± 0.3 | 0.47 ± 0.05 | >10−5 | |||
| NPMP | 8.0 ± 0.1 | 8.6 ± 0.2 | 6.2 ± 0.1 | >10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovach, I.M. Proton Bridging in Catalysis by and Inhibition of Serine Proteases of the Blood Cascade System. Life 2021, 11, 396. https://doi.org/10.3390/life11050396
Kovach IM. Proton Bridging in Catalysis by and Inhibition of Serine Proteases of the Blood Cascade System. Life. 2021; 11(5):396. https://doi.org/10.3390/life11050396
Chicago/Turabian StyleKovach, Ildiko M. 2021. "Proton Bridging in Catalysis by and Inhibition of Serine Proteases of the Blood Cascade System" Life 11, no. 5: 396. https://doi.org/10.3390/life11050396
APA StyleKovach, I. M. (2021). Proton Bridging in Catalysis by and Inhibition of Serine Proteases of the Blood Cascade System. Life, 11(5), 396. https://doi.org/10.3390/life11050396