An Experimental and Numerical Simulation Study of Single Particle Impact during Detonation Spraying
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Details
2.2. Analysis of the Experimental Samples
2.3. Details of SPH Simulation
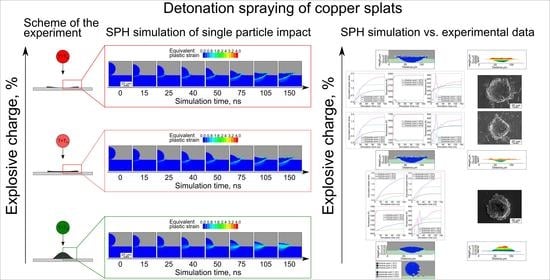
3. Results and Discussion
3.1. OM and SEM Results
3.2. Numerical Simulation Results
3.2.1. The Collision below the Melting Point
3.2.2. The Collision at Equal or above the Melting Point
3.3. Comparison of SPH-Simulation Results and Experimental Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tejero-Martin, D.; Rezvani Rad, M.; McDonald, A.; Hussain, T. Beyond Traditional Coatings: A Review on Thermal-Sprayed Functional and Smart Coatings. J. Therm. Spray Technol. 2019, 28, 598–644. [Google Scholar] [CrossRef] [Green Version]
- Ulianitsky, V.Y.; Batraev, I.S.; Shtertser, A.A.; Dudina, D.V.; Bulina, N.V.; Smurov, I. Detonation Spraying Behaviour of Refractory Metals: Case Studies for Mo and Ta-Based Powders. Adv. Powder Technol. 2018, 29, 1859–1864. [Google Scholar] [CrossRef]
- Chmielewski, T. Metallization of Aln Ceramic with Ti Using Detonation Spraying Process–Thermodynamic Approach. J. Manuf. Technol. 2018, 43, 11–19. [Google Scholar]
- Panin, S.; Vlasov, I.; Dudina, D.; Ulyanitsky, V.; Stankevich, R.; Batraev, I.; Maruschak, P.; Landová, M. Deposition of Titanium Based Coatings by Reactive Detonation Spraying. Koroze Ochr. Materiálu 2018, 62, 6–13. [Google Scholar] [CrossRef] [Green Version]
- Senderowski, C.; Chodala, M.; Bojar, Z. Corrosion Behavior of Detonation Gun Sprayed Fe-Al Type Intermetallic Coating. Materials 2015, 8, 1108–1123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dudina, D.V.; Korchagin, M.A.; Zlobin, S.B.; Ulianitsky, V.Y.; Lomovsky, O.I.; Bulina, N.V.; Bataev, I.A.; Bataev, V.A. Compositional Variations in the Coatings Formed by Detonation Spraying of Ti3Al at Different O2/C2H2 Ratios. Intermetallics 2012, 29, 140–146. [Google Scholar] [CrossRef]
- Kuchumova, I.; Batraev, I.; Cherkasova, N.; Ukhina, A.; Shtertser, A.; Jorge, A.M. The Influence of Salt Fog Exposure on Corrosion Resistance of Detonation Coatings Fe66Cr10Nb5B19. Met. Work. Mater. Sci. 2020, 22, 95–105. [Google Scholar] [CrossRef]
- Oliker, V.E.; Abdurashitova, S.A.; Martsenyuk, I.S.; Grechishkin, E.F.; Bondarenko, A.A. Microstructure and Properties of Detonation-Sprayed Thermal Barrier ZrO2 Coatings. Powder Metall. Met. Ceram. 2013, 52, 83–89. [Google Scholar] [CrossRef]
- Babu, P.S.; Sen, D.; Jyothirmayi, A.; Krishna, L.R.; Rao, D.S. Influence of Microstructure on the Wear and Corrosion Behavior of Detonation Sprayed Cr2O3-Al2O3 and Plasma Sprayed Cr2O3 Coatings. Ceram. Int. 2018, 44, 2351–2357. [Google Scholar] [CrossRef]
- Ulianitsky, V.; Shtertser, A.; Batraev, I. Electrical Insulation Properties of Aluminum Oxide Detonation Coatings. Met. Work. Mater. Sci. 2018, 20, 83–95. [Google Scholar] [CrossRef]
- Kantay, N.; Rakhadilov, B.; Kurbanbekov, S.; Yeskermessov, D.; Yerbolatova, G.; Apsezhanova, A. Influence of Detonation-Spraying Parameters on the Phase Composition and Tribological Properties of Al2O3 Coatings. Coatings 2021, 11, 793. [Google Scholar] [CrossRef]
- Du, H.; Hua, W.; Liu, J.; Gong, J.; Sun, C.; Wen, L. Influence of Process Variables on the Qualities of Detonation Gun Sprayed WC–Co Coatings. Mater. Sci. Eng. A 2005, 408, 202–210. [Google Scholar] [CrossRef]
- Babu, P.S.; Rao, P.C.; Jyothirmayi, A.; Phani, P.S.; Krishna, L.R.; Rao, D.S. Evaluation of Microstructure, Property and Performance of Detonation Sprayed WC-(W, Cr)2C-Ni Coatings. Surf. Coat. Technol. 2018, 335, 345–354. [Google Scholar] [CrossRef]
- Du, H.; Sun, C.; Hua, W.G.; Zhang, Y.S.; Han, Z.; Wang, T.G.; Gong, J.; Lee, S.W. Fabrication and Evaluation of D-Gun Sprayed WC–Co Coating with Self-Lubricating Property. Tribol. Lett. 2006, 23, 261–266. [Google Scholar] [CrossRef]
- Smurov, I.; Ulianitsky, V. Computer Controlled Detonation Spraying: A Spraying Process Upgraded to Advanced Applications. Surf. Eff. Contact Mech. 2011, 10, 265–276. [Google Scholar]
- Ulianitsky, V.Y.; Nenashev, M.V.; Kalashnikov, V.V.; Ibatullin, I.D.; Ganigin, S.Y.; Yakunin, K.P.; Rogozhin, P.V.; Shtertser, A.A. Opyt Issledovanija i Primenenija Tehnologii Nanesenija Detonacionnyh Pokrytij. Izvestija Samarskogo Nauchnogo Centra Rossijskoj Akademii Nauk 2010, 12, 569–575. [Google Scholar]
- Yildirim, B.; Muftu, S.; Gouldstone, A. Modeling of High Velocity Impact of Spherical Particles. Wear 2011, 270, 703–713. [Google Scholar] [CrossRef]
- Li, W.-Y.; Zhang, C.; Li, C.-J.; Liao, H. Modeling Aspects of High Velocity Impact of Particles in Cold Spraying by Explicit Finite Element Analysis. J. Therm. Spray Technol. 2009, 18, 921–933. [Google Scholar] [CrossRef]
- Li, W.-Y.; Liao, H.; Li, C.-J.; Li, G.; Coddet, C.; Wang, X. On High Velocity Impact of Micro-Sized Metallic Particles in Cold Spraying. Appl. Surf. Sci. 2006, 253, 2852–2862. [Google Scholar] [CrossRef]
- Manap, A.; Okabe, T.; Ogawa, K. Computer Simulation of Cold Sprayed Deposition Using Smoothed Particle Hydrodynamics. Procedia Eng. 2011, 10, 1145–1150. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Nélias, D.; Berre, W.-L.; Ogawa, K.; Ichikawa, Y. Simulation of the Cold Spray Particle Deposition Process. J. Tribol. 2015, 137, 041101. [Google Scholar] [CrossRef] [Green Version]
- Suresh, S.; Lee, S.-W.; Aindow, M.; Brody, H.D.; Champagne, V.K.; Dongare, A.M. Mesoscale Modeling of Jet Initiation Behavior and Microstructural Evolution during Cold Spray Single Particle Impact. Acta Mater. 2020, 182, 197–206. [Google Scholar] [CrossRef]
- Yin, S.; Wang, X.; Suo, X.; Liao, H.; Guo, Z.; Li, W.; Coddet, C. Deposition Behavior of Thermally Softened Copper Particles in Cold Spraying. Acta Mater. 2013, 61, 5105–5118. [Google Scholar] [CrossRef]
- Nikolaev, Y.A.; Vasil’ev, A.A.; Ul’yanitskii, B.Y. Gas Detonation and Its Application in Engineering and Technologies. Combust. Explos. Shock Waves 2003, 39, 382–410. [Google Scholar] [CrossRef]
- Batraev, I.S.; Ulianitsky, V.Y.; Dudina, D.V. Detonation Spraying of Copper: Theoretical Analysis and Experimental Studies. Mater. Today Proc. 2017, 4, 11346–11350. [Google Scholar] [CrossRef]
- Ulianitsky, V.Y.; Dudina, D.V.; Shtertser, A.A.; Smurov, I. Computer-Controlled Detonation Spraying: Flexible Control of the Coating Chemistry and Microstructure. Metals 2019, 9, 1244. [Google Scholar] [CrossRef] [Green Version]
- Gavrilenko, T.P.; Nikolaev, Y.A. Calculation of Detonation Gas Spraying. Combust. Explos. Shock Waves 2007, 43, 724–731. [Google Scholar] [CrossRef]
- Émurlaeva, Y.Y.; Bataev, I.A.; Zhou, Q.; Lazurenko, D.V.; Ivanov, I.V.; Riabinkina, P.A.; Tanaka, S.; Chen, P. Welding Window: Comparison of Deribas’ and Wittman’s Approaches and SPH Simulation Results. Metals 2019, 9, 1323. [Google Scholar] [CrossRef] [Green Version]
- Bataev, I. Structure of Explosively Welded Materials: Experimental Study and Numerical Simulation. Met. Work. Mater. Sci. 2017, 77, 55–67. [Google Scholar] [CrossRef]
- Nassiri, A.; Abke, T.; Daehn, G. Investigation of Melting Phenomena in Solid-State Welding Processes. Scr. Mater. 2019, 168, 61–66. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Inao, D.; Tanaka, S.; Hokamoto, K. Study of Explosive Welding of A6061/SUS821L1 Using Interlayers with Different Thicknesses and the Air Shockwave between Plates. Int. J. Adv. Manuf. Technol. 2021, 116, 3779–3794. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Yu, H.; Zhao, F.; Wu, Z. Numerical Simulation of Ti/Al Bimetal Composite Fabricated by Explosive Welding. Metals 2017, 7, 407. [Google Scholar] [CrossRef] [Green Version]
- Geng, H.; Mao, J.; Zhang, X.; Li, G.; Cui, J. Formation Mechanism of Transition Zone and Amorphous Structure in Magnetic Pulse Welded Al-Fe Joint. Mater. Lett. 2019, 245, 151–154. [Google Scholar] [CrossRef]
- Zhang, S.; Lueg-Althoff, J.; Hahn, M.; Tekkaya, A.E.; Kinsey, B. Effect of Process Parameters on Wavy Interfacial Morphology During Magnetic Pulse Welding. J. Manuf. Sci. Eng. 2021, 143, 011010. [Google Scholar] [CrossRef]
- Lueg-Althoff, J.; Bellmann, J.; Gies, S.; Schulze, S.; Tekkaya, A.E.; Beyer, E. Influence of the Flyer Kinetics on Magnetic Pulse Welding of Tubes. J. Mater. Process. Technol. 2018, 262, 189–203. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Feng, D.L.; Liu, M.B. Investigation of Explosive Welding through Whole Process Modeling Using a Density Adaptive SPH Method. J. Manuf. Process. 2018, 35, 169–189. [Google Scholar] [CrossRef]
- Alhussan, K.A.; Babenko, V.A.; Kozlov, I.M.; Smetannikov, A.S. Development of Modified SPH Approach for Modeling of High-Velocity Impact. Int. J. Heat Mass Transf. 2012, 55, 6340–6348. [Google Scholar] [CrossRef]
- Hassani-Gangaraj, M.; Veysset, D.; Champagne, V.K.; Nelson, K.A.; Schuh, C.A. Adiabatic Shear Instability Is Not Necessary for Adhesion in Cold Spray. Acta Mater. 2018, 158, 430–439. [Google Scholar] [CrossRef]
- Batraev, I.S.; Prohorov, E.S.; Ulianitsky, V.Y. Razgon I Nagrev Poroshkovyh Chastic Produktami Gazovoj Detonacii V Kanalah S Konicheskim Perehodom. Combust. Explos. Shock Waves 2014, 50, 315–322. (In Russian) [Google Scholar] [CrossRef]
- Ulianitsky, V.; Batraev, I.; Dudina, D.; Smurov, I. Enhancing the Properties of WC/Co Detonation Coatings Using Two-Component Fuels. Surf. Coat. Technol. 2017, 318, 244–249. [Google Scholar] [CrossRef]
- Ulianitsky, V.Y.; Batraev, I.S.; Shtertser, A.A. Detonacionnye pokrytija iz oksidov. Uprochnjajushhie Tehnologii I Pokrytija 2015, 9, 37–44. (In Russian) [Google Scholar]
- King, P.C.; Bae, G.; Zahiri, S.H.; Jahedi, M.; Lee, C. An Experimental and Finite Element Study of Cold Spray Copper Impact onto Two Aluminum Substrates. J. Therm. Spray Technol. 2010, 19, 620–634. [Google Scholar] [CrossRef]
- Assadi, H.; Gärtner, F.; Stoltenhoff, T.; Kreye, H. Bonding Mechanism in Cold Gas Spraying. Acta Mater. 2003, 51, 4379–4394. [Google Scholar] [CrossRef]











| Volume of the Barrel Filling with Explosive Mixture *, % | T, K | V, m/s |
|---|---|---|
| 65 | 1839 | 402 |
| 60 | 1558 | 405 |
| 50 | 1356 | 389 |
| 40 | 1231 | 338 |
| 35 | 1042 | 311 |
| Parameter | Value | Units |
|---|---|---|
| Density | 8900 | kg/m3 |
| Shear modulus | 44.7 | GPa |
| Thermal conductivity | 386.5 | W/m∙K |
| Specific heat | 383 | J/kg∙K |
| Sound speed | 3940 | m/s |
| Parameter S | 1.489 | - |
| Grüneisen parameter, Г0 | 2.02 | - |
| Yield stress, A | 90 | MPa |
| Hardening constant, B | 292 | MPa |
| Hardening exponent associated with quasi-static test, n | 0.31 | - |
| Strain rate constant, C | 0.025 | - |
| Thermal softening exponent, m | 1.09 | - |
| Melting temperature | 1356 | K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riabinkina, P.A.; Bataev, I.A.; Batraev, I.S.; Ruktuev, A.A.; Ulianitsky, V.Y.; Tanaka, S.; Emurlaeva, Y.Y.; Ogneva, T.S.; Bataev, V.A. An Experimental and Numerical Simulation Study of Single Particle Impact during Detonation Spraying. Metals 2022, 12, 1013. https://doi.org/10.3390/met12061013
Riabinkina PA, Bataev IA, Batraev IS, Ruktuev AA, Ulianitsky VY, Tanaka S, Emurlaeva YY, Ogneva TS, Bataev VA. An Experimental and Numerical Simulation Study of Single Particle Impact during Detonation Spraying. Metals. 2022; 12(6):1013. https://doi.org/10.3390/met12061013
Chicago/Turabian StyleRiabinkina, Polina A., Ivan A. Bataev, Igor S. Batraev, Alexey A. Ruktuev, Vladimir Yu. Ulianitsky, Shigeru Tanaka, Yulia Yu. Emurlaeva, Tatiana S. Ogneva, and Vladimir A. Bataev. 2022. "An Experimental and Numerical Simulation Study of Single Particle Impact during Detonation Spraying" Metals 12, no. 6: 1013. https://doi.org/10.3390/met12061013
APA StyleRiabinkina, P. A., Bataev, I. A., Batraev, I. S., Ruktuev, A. A., Ulianitsky, V. Y., Tanaka, S., Emurlaeva, Y. Y., Ogneva, T. S., & Bataev, V. A. (2022). An Experimental and Numerical Simulation Study of Single Particle Impact during Detonation Spraying. Metals, 12(6), 1013. https://doi.org/10.3390/met12061013