Microstructure, Texture Evolution and Mechanical Properties of VT3-1 Titanium Alloy Processed by Multi-Pass Drawing and Subsequent Isothermal Annealing
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
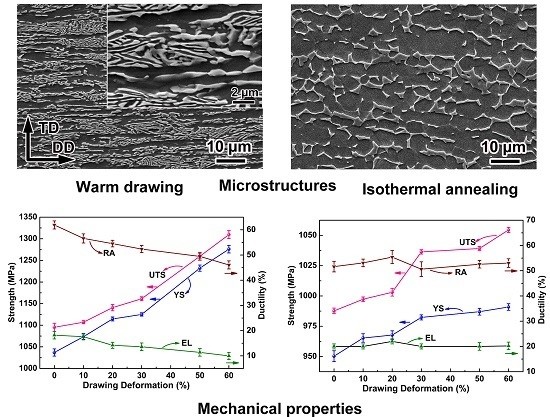
3.1. Microstructure Characteristics
3.2. X-ray Diffraction (XRD) and Texture Analysis
3.3. Mechanical Properties
4. Conclusions
- (1)
- For drawn samples, α grains are gradually elongated along the drawing direction with increasing deformation, and a fiber-like microstructure is formed after 60% warm-drawing deformation. After isothermal annealing, the microstructure is more homogeneous with increasing deformation, although the volume fraction of the α phase is similar.
- (2)
- The fiber texture with orientations around the position of {φ1 = 10°, φ = 65°, φ2 = 0°}, i.e., close to (22)[100], gradually becomes the major and stable type of texture during warm drawing. For IA samples, the textures during recrystallization show significant increases in texture intensity and in volume fraction compared to their deformed states due to a preferential grain growth along the orientation of original deformation textures. However, for the 60% + IA samples, the major orientation has been shifted into a new one with c-axis titled ~20° compared with {φ1 = 10°, φ = 65°, φ2 = 0°}. The texture indices for deformed and annealed states are sensitive within the 30% drawing deformation.
- (3)
- The samples processed by multi-pass warm drawing exhibit high strength and low ductility owing to significant grain refinement and work hardening. For IA samples, a high and stable ductility is obtained. Moreover, a negative slope of yield strength versus d−1/2 is observed as a result of texture softening in as-received + IA samples but texture hardening in drawn + IA samples. The relationship between texture and yield strength indicates that texture developed during drawing is beneficial to improving strength of IA states.
Author Contributions
Conflicts of Interest
References
- Lütjering, G.; Williams, J.C. Titanium, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 203–250. [Google Scholar]
- Liu, Y.J.; Li, X.P.; Zhang, L.C.; Sercombe, T.B. Processing and properties of topologically optimised biomedical Ti–24Nb–4Zr–8Sn scaffolds manufactured by selective laser melting. Mater. Sci. Eng. A 2015, 642, 268–278. [Google Scholar] [CrossRef]
- Cui, C.; Hu, B.M.; Zhao, L.; Liu, S. Titanium alloy production technology, market prospects and industry development. Mater. Des. 2011, 32, 1684–1691. [Google Scholar] [CrossRef]
- Ehtemam-Haghighi, S.; Liu, Y.J.; Cao, G.; Zhang, L.C. Influence of Nb on the β → α martensitic phase transformation and properties of the newly designed Ti–Fe–Nb alloys. Mater. Sci. Eng. C 2015, 60, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Xiong, A.; Huang, W.; Wang, H.; Su, S.; Shen, L. Microstructural evolution and modelling of the hot compression of a TC6 titanium alloy. Mater. Charact. 2002, 49, 203–209. [Google Scholar] [CrossRef]
- Ghasemi, E.; Zarei-Hanzaki, A.; Moemeni, S.; Ghambari, M.; Rezaee, M. An investigation into the warm deformation behavior of Ti–6Al–1.5Cr–2.5Mo–0.5Fe–0.3Si alloy. Mater. Sci. Eng. A 2016, 654, 264–270. [Google Scholar] [CrossRef]
- Kim, W.J.; Hong, S.I.; Kim, Y.S.; Min, S.H.; Jeong, H.T.; Lee, J.D. Texture development and its effect on mechanical properties of an AZ61 Mg alloy fabricated by equal channel angular pressing. Acta Mater. 2003, 51, 3293–3307. [Google Scholar] [CrossRef]
- Zhang, L.C.; Attar, H. Selective Laser Melting of Titanium Alloys and Titanium Matrix Composites for Biomedical Applications: A Review. Adv. Eng. Mater. 2016, 18, 463–475. [Google Scholar] [CrossRef]
- Zhao, A.M.; Yang, H.; Fan, X.G.; Gao, P.F.; Zuo, R.; Meng, M. The flow behavior and microstructure evolution during (α + β) deformation of β wrought TA15 titanium alloy. Mater. Des. 2016, 109, 112–122. [Google Scholar] [CrossRef]
- Bieler, T.R.; Semiatin, S.L. The origins of heterogeneous deformation during primary hot working of Ti–6Al–4V. Int. J. Plast. 2002, 18, 1165–1189. [Google Scholar] [CrossRef]
- Bridier, F.; Villechaise, P.; Mendez, J. Analysis of the different slip systems activated by tension in a α/β titanium alloy in relation with local crystallographic orientation. Acta Mater. 2005, 53, 555–567. [Google Scholar] [CrossRef]
- Ehtemam-Haghighi, S.; Liu, Y.J.; Cao, G.; Zhang, L.C. Phase transition, microstructural evolution and mechanical properties of Ti–Nb–Fe alloys induced by Fe addition. Mater. Des. 2016, 97, 279–286. [Google Scholar] [CrossRef]
- Fizanne-Michel, C.; Cornen, M.; Castany, P.; Péron, I.; Gloriant, T. Determination of hardness and elastic modulus inverse pole figures of a polycrystalline commercially pure titanium by coupling nanoindentation and EBSD techniques. Mater. Sci. Eng. A 2014, 613, 159–162. [Google Scholar] [CrossRef]
- Wang, Y.N.; Huang, J.C. Texture analysis in hexagonal materials. Mater. Chem. Phys. 2003, 81, 11–26. [Google Scholar] [CrossRef]
- Germain, L.; Gey, N.; Humbert, M.; Bocher, P.; Jahazi, M. Analysis of sharp microtexture heterogeneities in a bimodal IMI 834 billet. Acta Mater. 2005, 53, 3535–3543. [Google Scholar] [CrossRef]
- Gey, N.; Bocher, P.; Uta, E.; Germain, L.; Humbert, M. Texture and microtexture variations in a near-α titanium forged disk of bimodal microstructure. Acta Mater. 2012, 60, 2647–2655. [Google Scholar] [CrossRef]
- Wagner, F.; Bozzolo, N.; Landuyt, O.V.; Grosdidier, T. Evolution of recrystallisation texture and microstructure in low alloyed titanium sheets. Acta Mater. 2002, 50, 1245–1259. [Google Scholar] [CrossRef]
- Bozzolo, N.; Dewobroto, N.; Grosdidier, T.; Wagner, F. Texture evolution during grain growth in recrystallized commercially pure titanium. Mater. Sci. Eng. A 2005, 397, 346–355. [Google Scholar] [CrossRef]
- Warwick, J.L.W.; Jones, N.G.; Bantounas, I.; Preuss, M.; Dye, D. In situ observation of texture and microstructure evolution during rolling and globularization of Ti–6Al–4V. Acta Mater. 2013, 61, 1603–1615. [Google Scholar] [CrossRef]
- Hayama, A.O.F.; Lopes, J.F.S.C.; Silva, M.J.G.D.; Abreu, H.F.G.; Caram, R. Crystallographic texture evolution in Ti–35Nb alloy deformed by cold rolling. Mater. Des. 2014, 60, 653–660. [Google Scholar] [CrossRef]
- Cojocaru, V.D.; Raducanu, D.; Gloriant, T.; Gordin, D.M.; Cinca, I. Effects of cold-rolling deformation on texture evolution and mechanical properties of Ti–29Nb–9Ta–10Zr alloy. Mater. Sci. Eng. A 2013, 586, 1–10. [Google Scholar] [CrossRef]
- Prakash, D.G.L.; Honniball, P.; Rugg, D.; Withers, P.J.; Fonseca, J.Q.D.; Preuss, M. The effect of β phase on microstructure and texture evolution during thermomechanical processing of α + β Ti alloy. Acta Mater. 2013, 61, 3200–3213. [Google Scholar] [CrossRef]
- Du, Z.; Xiao, S.; Liu, J.; Lv, S.; Xu, L.; Kong, F.; Chen, Y. Hot deformation behavior of Ti–3.5Al–5Mo–6V–3Cr–2Sn–0.5Fe alloy in α + β field. Metals 2015, 5, 216–227. [Google Scholar] [CrossRef]
- Lium, Y.J.; Lim, S.J.; Wangm, H.L.; Houm, W.T.; Haom, Y.L.; Yangm, R.; Sercombem, T.B.; Zhang, L.C. Microstructure, defects and mechanical behavior of beta-type titanium porous structures manufactured by electron beam melting and selective laser melting. Acta Mater. 2016, 113, 56–67. [Google Scholar]
- Zaefferer, S. A study of active deformation systems in titanium alloys: Dependence on alloy composition and correlation with deformation texture. Mater. Sci. Eng. A 2003, 344, 20–30. [Google Scholar] [CrossRef]
- Zhao, T.Z.; Zhang, G.L.; Song, H.W.; Cheng, M.; Zhang, S.H. Crystallographic texture difference between center and sub-surface of thin cold-drawn pearlitic steel wires. J. Mater. Eng. Perform. 2014, 23, 3279–3284. [Google Scholar] [CrossRef]
- Lee, J.W.; Baek, H.M.; Sun, K.H.; Son, I.H.; Bae, C.M.; Im, Y.T. The effect of the multi-pass non-circular drawing sequence on mechanical properties and microstructure evolution of low-carbon steel. Mater. Des. 2014, 55, 898–904. [Google Scholar] [CrossRef]
- Dai, N.; Zhang, L.C.; Zhang, J.; Chen, Q.; Wu, M. Corrosion behaviour of selective laser melted Ti–6Al–4V alloy in NaCl solution. Corros. Sci. 2016, 102, 484–489. [Google Scholar] [CrossRef]
- Zhang, L.C.; Das, J.; Lu, H.B.; Duhamel, C.; Calin, M.; Eckert, J. High strength Ti–Fe–Sn ultrafine composites with large plasticity. Scr. Mater. 2007, 57, 101–104. [Google Scholar] [CrossRef]
- Dahms, M.; Bunge, H.J. The iterative series-expansion method for quantitative texture analysis. I. General outline. J. Appl. Crystallogr. 1989, 22, 439–447. [Google Scholar] [CrossRef]
- Robertson, S.W.; Gong, X.Y.; Ritchie, R.O. Effect of product form and heat treatment on the crystallographic texture of austenitic Nitinol. J. Mater. Sci. 2006, 41, 621–630. [Google Scholar] [CrossRef]
- Schillinger, W.; Bartels, A.; Gerling, R.; Schimansky, F.P.; Clemens, H. Texture evolution of the γ- and the α/α2-phase during hot rolling of γ-TiAl based alloys. Intermetallics 2006, 14, 336–347. [Google Scholar] [CrossRef]
- Ghamarian, I.; Hayes, B.; Samimi, P.; Welk, B.A.; Fraser, H.L.; Collins, P.C. Developing a phenomenological equation to predict yield strength from composition and microstructure in β processed Ti–6Al–4V. Mater. Sci. Eng. A 2016, 660, 172–180. [Google Scholar] [CrossRef]
- Leyens, C.; Peters, M. Titanium and Titanium Alloys: Fundamentals and Applications, 1st ed.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2003; pp. 112–114. [Google Scholar]
- Kumar, S.S.S.; Priyasudha, K.; Rao, M.S.; Raghu, T. Deformation homogeneity, mechanical behaviour and strain hardening characteristics of titanium severe plastically deformed by cyclic channel die compression method. Mater. Des. 2016, 101, 117–129. [Google Scholar] [CrossRef]
- Nan, X.L.; Wang, H.Y.; Zhang, L.; Li, J.B.; Jiang, Q.C. Calculation of Schmid factors in magnesium: Analysis of deformation behaviors. Scr. Mater. 2012, 67, 443–446. [Google Scholar] [CrossRef]
- Li, H.; Mason, D.E.; Bieler, T.R.; Boehlert, C.J.; Crimp, M.A. Methodology for estimating the critical resolved shear stress ratios of α-phase Ti using EBSD-based trace analysis. Acta Mater. 2013, 61, 7555–7567. [Google Scholar] [CrossRef]
- Liu, Y.J.; Wang, H.L.; Li, S.J.; Wang, S.G.; Wang, W.J.; Hou, W.T.; Hao, Y.L.; Yang, R.; Zhang, L.C. Compressive and fatigue behavior of beta-type titanium porous structures fabricated by electron beam melting. Acta Mater. 2017, 126, 58–66. [Google Scholar] [CrossRef]
- Liu, Y.J.; Li, S.J.; Hou, W.T.; Wang, S.G.; Hao, Y.L.; Yang, R.; Sercombe, T.B.; Zhang, L.C. Electron beam melted beta-type Ti–24Nb–4Zr–8Sn porous structures with high strength-to-modulus ratio. J. Mater. Sci. Technol. 2016, 32, 505–508. [Google Scholar] [CrossRef]
- Fundenberger, J.J.; Philippe, M.J.; Wagner, F.; Esling, C. Modelling and prediction of mechanical properties for materials with hexagonal symmetry (zinc, titanium and zirconium alloys). Acta Mater. 1997, 45, 4041–4055. [Google Scholar] [CrossRef]









| Sample State | Diameter, mm | Area Reduction, % | Accumulated Strain |
|---|---|---|---|
| As received | 25.40 | 0 | 0 |
| 30% warm-drawn | 20.90 | 32.3 | 0.39 |
| 60% warm-drawn | 16.18 | 59.4 | 0.90 |
| Sample State | Euler Angles, ° | Orientation Density | Texture Component, ~(hkil)[uvtw] | Volume Fraction, % | Texture Index | ||
|---|---|---|---|---|---|---|---|
| φ1 | φ | φ2 | |||||
| As-received | 0 | 70 | 30 | 6.22 | (011)[20] | 2.67 | 2.51 |
| 15 | 60 | 0 | 5.16 | (22)[100] | 2.87 | ||
| 0 | 0 | 0 | 4.36 | (0001)[100] | 3.90 | ||
| 30% warm-drawn | 15 | 65 | 0 | 7.60 | (22)[100] | 4.46 | 4.25 |
| 0 | 25 | 10 | 4.69 | (39)[100] | 3.89 | ||
| 60% warm-drawn | 10 | 65 | 0 | 8.62 | (22)[100] | 5.29 | 4.53 |
| 0 | 35 | 0 | 5.53 | (25)[100] | 5.16 | ||
| As-received + IA | 15 | 60 | 0 | 7.23 | (22)[100] | 2.94 | 3.77 |
| 0 | 65 | 30 | 6.58 | (011)[20] | 3.17 | ||
| 0 | 15 | 0 | 5.36 | (0001)[100] | 3.76 | ||
| 30% + IA | 10 | 65 | 0 | 10.75 | (22)[100] | 6.12 | 8.09 |
| 0 | 70 | 30 | 6.04 | (011)[20] | 4.91 | ||
| 60% + IA | 15 | 45 | 0 | 10.83 | (23)[100] | 8.39 | 10.95 |
| 0 | 10 | 0 | 7.77 | (0001)[100] | 7.16 | ||
| 0 | 60 | 30 | 6.92 | (011)[20] | 4.64 | ||
| Texture Component, ~(hkil)[uvtw] | Schmid Factor | |||
|---|---|---|---|---|
| Basal <a>, {0001}<110> | Prismatic <a>, {100}<110> | Pyramidal <a>, {101}<110> | Pyramidal <c + a>, {101}<113> | |
| (011)[20] | 0; 0; 0 | 0.43 *; 0.43; 0 | 0; 0; 0.38; 0.38; 0.38; 0.38 | 0.2; 0.4; 0.2; 0.4; 0.4; 0.2; 0; 0; 0; 0; 0; 0 |
| (22)[100] | 0.13; 0.12; 0.14 | 0.45; 0.07; 0.38 | 0.30; 0.37; 0.01; 0.14; 0.44; 0.36 | 0.05; 0.19; 0.07; 0.25; 0.32; 0.28; 0.48 *; 0.45; 0.08; 0.14; 0.03; 0.17 |
| (0001)[100] | 0; 0; 0 | 0.43; 0; 0.43 * | 0.38; 0.38; 0; 0; 0.38; 0.38 | 0; 0.2; 0; 0.2; 0.4; 0.4; 0.4; 0.4; 0; 0.2; 0; 0.2 |
| (39)[100] | 0; 0; 0 | 0.49 *; 0.17; 0.32 | 0.28; 0.28; 0.15; 0.15; 0.43; 0.43 | 0.05; 0.28; 0.05; 0.28; 0.43; 0.35; 0.43; 0.35; 0.03; 0.12; 0.03; 0.12 |
| (25)[100] | 0; 0; 0 | 0.43 *; 0; 0.43 | 0.38; 0.38; 0; 0; 0.38; 0.38 | 0; 0.2; 0; 0.2; 0.4; 0.4; 0.4; 0.4; 0; 0.2; 0; 0.2 |
| (23)[100] | 0.14; 0.03; 0.17 | 0.47; 0.18; 0.3 | 0.24; 0.29; 0.07; 0.24; 0.47; 0.36 | 0.04; 0.22; 0.12; 0.31; 0.32; 0.22; 0.49 *; 0.42; 0.09; 0.09; 0.01; 0.11 |
| Sample State | Calculated Yield Stress, MPa |
|---|---|
| As-received | 884.6 |
| 30% warm-drawn | 901.2 |
| 60% warm-drawn | 907.7 |
| As-received + IA | 875.5 |
| 30% + IA | 910.6 |
| 60% + IA | 913.4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, X.; Dong, L.; Zhang, Z.; Liu, Y.; Hao, Y.; Yang, R.; Zhang, L.-C. Microstructure, Texture Evolution and Mechanical Properties of VT3-1 Titanium Alloy Processed by Multi-Pass Drawing and Subsequent Isothermal Annealing. Metals 2017, 7, 131. https://doi.org/10.3390/met7040131
Lei X, Dong L, Zhang Z, Liu Y, Hao Y, Yang R, Zhang L-C. Microstructure, Texture Evolution and Mechanical Properties of VT3-1 Titanium Alloy Processed by Multi-Pass Drawing and Subsequent Isothermal Annealing. Metals. 2017; 7(4):131. https://doi.org/10.3390/met7040131
Chicago/Turabian StyleLei, Xiaofei, Limin Dong, Zhiqiang Zhang, Yujing Liu, Yulin Hao, Rui Yang, and Lai-Chang Zhang. 2017. "Microstructure, Texture Evolution and Mechanical Properties of VT3-1 Titanium Alloy Processed by Multi-Pass Drawing and Subsequent Isothermal Annealing" Metals 7, no. 4: 131. https://doi.org/10.3390/met7040131
APA StyleLei, X., Dong, L., Zhang, Z., Liu, Y., Hao, Y., Yang, R., & Zhang, L. -C. (2017). Microstructure, Texture Evolution and Mechanical Properties of VT3-1 Titanium Alloy Processed by Multi-Pass Drawing and Subsequent Isothermal Annealing. Metals, 7(4), 131. https://doi.org/10.3390/met7040131