Three-Dimensional Numerical Modeling of Macrosegregation in Continuously Cast Billets
Abstract
:1. Introduction
2. Model Formulation
2.1. Assumptions
- (a)
- An incompressible Newtonian fluid was assumed and the effects of turbulence were approximated with the low Reynolds number turbulence model.
- (b)
- Homogeneous and isotropic properties were assumed for steel in the simulation.
- (c)
- Local thermodynamic equilibrium was assumed at the solid–liquid interface.
- (d)
- The densities of liquid and solid were assumed to be constant and equal. Thus, the macrosegregation induced by shrinkage was not considered.
- (e)
- The effect of strand deformation (bulging [19]) and pore formation on the solute distribution was neglected.
- (f)
- Only the influence of billet curvature on macrosegregation was considered, and the force resulting from bending was ignored. The solid velocity in the whole computational domain was assumed to be equal to the casting speed.
- (g)
- The effects of remelting and sedimentation of grains on the segregation calculation were neglected.
2.2. Conservation Equations
2.2.1. Continuity Equation
2.2.2. Momentum Equation
2.2.3. Turbulence Model
2.2.4. Energy Equation
2.2.5. Species Equation
3. Computational Procedure
3.1. Reconstruction of Gravitational Acceleration
3.2. Numerical Scheme
3.3. Boundary Conditions
3.3.1. Meniscus
3.3.2. Inlet and Outlet
3.3.3. Moving Wall
4. Results and Discussion
4.1. Fluid Flow and Solidification
4.2. Solute Distribution and Validation
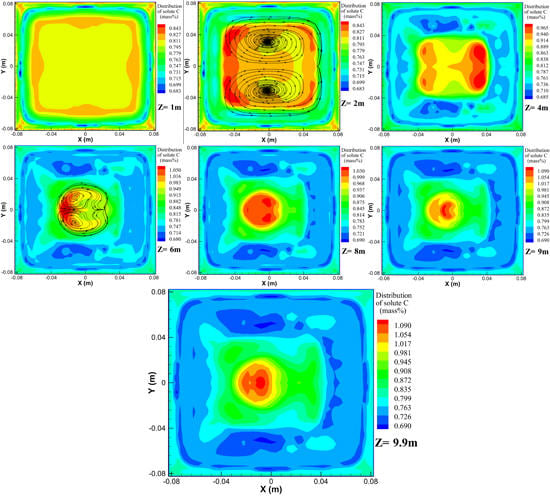
4.3. Evolution of Macrosegregation
4.4. Comparison between Different Elements
5. Conclusions
- (1)
- Flow patterns showed a significant melt recirculation around the impinging jet at the upper region of the mold. Two other relatively weak melt recirculation zones appeared in response to the backflow of molten steel. There was larger velocity at the corner than the edge near the solidification shell.
- (2)
- The solidification model applied in this work was validated according to surface temperature measurements. The relatively high cooling intensity created a thicker solidified shell at the diagonal section compared to the longitudinal section. Melt recirculation and washing effects further created uneven distribution of the solidified shell at the longitudinal section. The simulation results indicated thermosolutal convection at the secondary cooling zone, which resulted in asymmetrical distribution of the velocity and liquid fraction.
- (3)
- As convection, diffusion, and solidification progressed, there was measurable inhomogeneity in the solute distribution in the mold mainly occurring as solute enrichment at the upper region and negative segregation in the solidified shell. The distribution of different solute elements was predicted to be qualitatively similar.
- (4)
- The results also suggest that the final macrosegregation patterns in the billet formed in the mushy zone with relatively low central liquid fraction, but not at the end of solidification. The segregation profiles of solute C, arising with a positively segregated peak at the centerline and a negatively segregated minima at the sides, were predicted to be similar at the longitudinal and diagonal sections. There was close agreement between the measured and calculated segregation degrees, which supports the validity of the proposed 3D macrosegregation model.
- (5)
- The predicted ring-shaped negative segregation zone that formed in the mold still existed at the end of solidification due to the limited solute diffusion coefficient in solid. The solute redistribution occurring at the solidification front created solute-enriched liquid near the solidified shell, which contributed to the evolution of macrosegregation alongside thermosolutal convection.
- (6)
- The equilibrium partition coefficient was the main contributor to the distinctions in the magnitude of macrosegregation. Comparison between solutes P and S indicated that diffusion coefficients also have a certain influence on macrosegregation.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moon, C.H.; Oh, K.S.; Lee, J.D.; Lee, S.J.; Lee, Y. Effect of the roll surface profile on centerline segregation in soft reduction process. ISIJ Int. 2012, 52, 1266–1272. [Google Scholar] [CrossRef]
- Sang, B.; Kang, X.; Li, D. A novel technique for reducing macrosegregation in heavy steel ingots. J. Mater. Process. Technol. 2010, 210, 703–711. [Google Scholar] [CrossRef]
- Flemings, M.C.; Nereo, G.E. Macrosegregation. PT. 1. AIME Met. Soc. Trans. 1967, 239, 1449–1461. [Google Scholar]
- Mehrabian, R.; Keane, M.; Flemings, M.C. Interdendritic fluid flow and macrosegregation; influence of gravity. Metall. Mater. Trans. 1970, 1, 1209–1220. [Google Scholar] [CrossRef]
- Fujii, T.; Poirier, D.R.; Flemings, M.C. Macrosegregation in a multicomponent low alloy steel. Metall. Mater. Trans. B 1979, 10, 331–339. [Google Scholar] [CrossRef]
- Bennon, W.D.; Incropera, F.P. A continuum model for momentum, heat and species transport in binary solid-liquid phase change systems—I. Model formulation. Int. J. Heat Mass Transf. 1987, 30, 2161–2170. [Google Scholar] [CrossRef]
- Poole, G.M.; Heyen, M.; Nastac, L.; El-Kaddah, N. Numerical modeling of macrosegregation in binary alloys solidifying in the presence of electromagnetic stirring. Metall. Mater. Trans. B 2014, 45, 1834–1841. [Google Scholar] [CrossRef]
- Ni, J.; Beckermann, C. A volume-averaged two-phase model for transport phenomena during solidification. Metall. Trans. B 1991, 22, 349–361. [Google Scholar] [CrossRef]
- Zhao, X.K.; Zhang, J.M.; Lei, S.W.; Wang, Y.N. The position study of heavy reduction process for improving centerline segregation or porosity with extra-thickness slabs. Steel Res. Int. 2014, 85, 645–658. [Google Scholar] [CrossRef]
- Li, W.S.; Shen, H.F.; Zhang, X.; Liu, B.C. Modeling of species transport and macrosegregation in heavy steel ingots. Metall. Mater. Trans. B 2014, 45, 464–471. [Google Scholar] [CrossRef]
- Koshikawa, T.; Bellet, M.; Gandin, C.A.; Yamamura, H.; Bobadilla, M. Experimental study and two-phase numerical modeling of macrosegregation induced by solid deformation during punch pressing of solidifying steel ingots. Acta Mater. 2017, 124, 513–527. [Google Scholar] [CrossRef]
- Wu, M.H.; Ludwig, A. A three-phase model for mixed columnar-equiaxed solidification. Metall. Mater. Trans. A 2006, 37, 1613–1631. [Google Scholar] [CrossRef]
- Ge, H.H.; Li, J.; Han, X.J.; Xia, M.X.; Li, J.G. Dendritic model for macrosegregation prediction of large scale castings. J. Mater. Process. Technol. 2016, 227, 308–317. [Google Scholar] [CrossRef]
- Vušanović, I.; Vertnik, R.; Šarler, B. A simple slice model for prediction of macrosegregation in continuously cast billets. IOP Conf. Ser. Mater. Sci. Eng. 2012, 27, 1–6. [Google Scholar] [CrossRef]
- Sun, H.B.; Zhang, J.Q. Study on the macrosegregation behavior for the bloom continuous casting: Model development and validation. Metall. Mater. Trans. B 2014, 45, 1133–1149. [Google Scholar] [CrossRef]
- Yang, H.L.; Zhang, X.Z.; Deng, K.W.; Li, W.C.; Gan, Y.; Zhao, L.G. Mathematical simulation on coupled flow, heat, and solute transport in slab continuous casting process. Metall. Mater. Trans. B 1998, 29, 1345–1356. [Google Scholar] [CrossRef]
- Fang, Q.; Ni, H.W.; Wang, B.; Zhang, H.; Ye, F. Effects of EMS induced flow on solidification and solute transport in bloom mold. Metals 2017, 7, 72. [Google Scholar] [CrossRef]
- Voller, V.R.; Beckermann, C. A unified model of microsegregation and coarsening. Metall. Mater. Trans. A 1999, 30, 2183–2189. [Google Scholar] [CrossRef]
- Domitner, J.; Wu, M.H.; Kharicha, A.; Ludwig, A.; Kaufmann, B.; Reiter, J. Modeling the effects of strand surface bulging and mechanical soft reduction on the macrosegregation formation in steel continuous casting. Metall. Mater. Trans. A 2014, 45, 1415–1434. [Google Scholar] [CrossRef]
- Won, Y.M.; Thomas, B.G. Simple model of microsegregation during solidification of steels. Metall. Mater. Trans. A 2001, 32, 1755–1767. [Google Scholar] [CrossRef]
- Prescott, P.J.; Incropera, F.P. The effect of turbulence on solidification of a binary metal alloy with electromagnetic stirring. J. Heat Transf. 1995, 117, 716–724. [Google Scholar] [CrossRef]
- Mathur, A.; He, S. Performance and implementation of the Launder–Sharma low-Reynolds number turbulence model. Comput. Fluids 2013, 79, 134–139. [Google Scholar] [CrossRef]
- Schneider, M.C.; Beckermann, C. A numerical study of the combined effects of microsegregation, mushy zone permeability and flow, caused by volume contraction and thermosolutal convection, on macrosegregation and eutectic formation in binary alloy solidification. Int. J. Heat Mass Transf. 1995, 38, 3455–3473. [Google Scholar] [CrossRef]
- Dong, Q.P.; Zhang, J.M.; Qian, L.; Yin, Y.B. Numerical modeling of macrosegregation in round billet with different microsegregation models. ISIJ Int. 2017, 57, 814–823. [Google Scholar] [CrossRef]
- Kang, K.G.; Ryou, H.S. Computation of solidification and melting using the PISO algorithm. Numer. Heat Transf. Part B Fund. 2010, 46, 179–194. [Google Scholar] [CrossRef]
- Du, P.F. Numerical Modeling of Porosity and Macrosegregation in Continuous Casting of Steel. Ph.D. Thesis, University of Iowa, Iowa City, IA, USA, 2013. [Google Scholar]
- Lai, K.Y.M.; Salcudean, M.; Tanaka, S.; Guthrie, R.I.L. Mathematical modeling of flows in large tundish systems in steelmaking. Metall. Mater. Trans. B 1986, 17, 449–459. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Singh, R.K.; Patwari, K.; Majumdar, S.; Ray, A.K.; Singh, A.K.P.; Neogi, N. Design and implementation of an automated secondary cooling system for the continuous casting of billets. ISA Trans. 2010, 49, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.F.; Chen, Y.; Li, D.Z.; Liu, H.W.; Fu, P.X. Comparison of channel segregation formation in model alloys and steels via numerical simulations. Metall. Mater. Trans. A 2016, 47, 2927–2939. [Google Scholar] [CrossRef]
- Ludwig, A.; Wu, M.H.; Kharicha, A. On macrosegregation. Metall. Mater. Trans. A 2015, 46, 4854–4867. [Google Scholar] [CrossRef]
- Clyne, T.W.; Kurz, W. Solute redistribution during solidification with rapid solid state diffusion. Metall. Mater. Trans. A 1981, 12, 965–971. [Google Scholar] [CrossRef]















| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 0.09 | 1.92 | ||
| 1.0 | 1.0 | ||
| 1.3 | |||
| 1.44 | |||
| 0.9 | 1.0 |
| Element | (wt %) | (-) | (1/wt %) | (m2/s) | (m2/s) |
|---|---|---|---|---|---|
| C | 0.81 | 0.34 | 0.0110 | ||
| Si | 0.19 | 0.52 | 0.0119 | ||
| Mn | 0.8 | 0.78 | 0.0019 | ||
| P | 0.015 | 0.13 | 0.0115 | ||
| S | 0.008 | 0.035 | 0.0123 |
| Parameters | Values |
|---|---|
| Casting speed, m/min | 1.65 |
| Pouring temperature, K | 1758 |
| Mold length, m | 0.8 |
| Length of secondary cooling zone, m | 6.65 |
| Length of air cooling zone, m | 2.55 |
| SEN depth from meniscus, m | 0.1 |
| SEN inner diameter, m | 0.035 |
| SEN outer diameter, m | 0.075 |
| Density, kg/m3 | 7340 |
| Solid specific heat, J/(kg·K) | 650 |
| Liquid thermal conductivity, W/(m·K) | 33.5 |
| Solid thermal conductivity, W/(m·K) | 24.7 |
| Thermal expansion coefficient, K−1 | 2.0 × 10−4 |
| Liquid viscosity, Pa·s | 0.00461 |
| Latent heat, J/kg | 231,637 |
| Fusion temperature of pure iron, K | 1808 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Q.; Zhang, J.; Yin, Y.; Wang, B. Three-Dimensional Numerical Modeling of Macrosegregation in Continuously Cast Billets. Metals 2017, 7, 209. https://doi.org/10.3390/met7060209
Dong Q, Zhang J, Yin Y, Wang B. Three-Dimensional Numerical Modeling of Macrosegregation in Continuously Cast Billets. Metals. 2017; 7(6):209. https://doi.org/10.3390/met7060209
Chicago/Turabian StyleDong, Qipeng, Jiongming Zhang, Yanbin Yin, and Bo Wang. 2017. "Three-Dimensional Numerical Modeling of Macrosegregation in Continuously Cast Billets" Metals 7, no. 6: 209. https://doi.org/10.3390/met7060209
APA StyleDong, Q., Zhang, J., Yin, Y., & Wang, B. (2017). Three-Dimensional Numerical Modeling of Macrosegregation in Continuously Cast Billets. Metals, 7(6), 209. https://doi.org/10.3390/met7060209