On the Mn–C Short-Range Ordering in a High-Strength High-Ductility Steel: Small Angle Neutron Scattering and Ab Initio Investigation
Abstract
:1. Introduction
2. Material and Methods
2.1. Material
2.2. Small Angle Neutron Scattering (SANS)
2.2.1. SANS Technique
2.2.2. SANS Experiments
2.3. Structural Models and Ab Initio Computational Details
3. Results
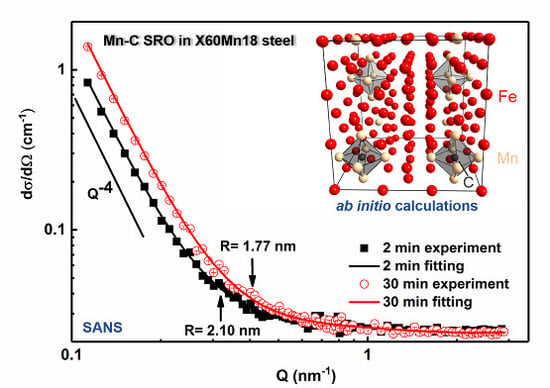
3.1. Small Angle Neutron Scattering (SANS)
3.2. Ab Initio Calculations
3.3. Microstructure and Mechanical Properties
4. Discussion
5. Conclusions
- (1)
- With an increase in annealing time from 2 min to 30 min, the size of the Mn–C SRO decreases, whereas their number density increases. The material exhibits a more evenly dispersed distribution of smaller clusters at longer annealing time during recrystallization.
- (2)
- The ab initio calculations qualitatively demonstrate that an increase in Mn neighbors of C in the 1st coordination sphere, resulting in a Mn6C octahedron, is energetically favorable, confirming prior studies on the Mn–C interaction. However, in non-idealized, “realistic” models, these effects are far less pronounced and energetic scattering is higher.
- (3)
- The repulsive C–C interaction is an equally important effect, which can counteract the Mn–C attraction, resulting in the formation of Mn6C units that are distributed evenly rather than being closely grouped, and they keep minimum distances from each other. This confirms and expands upon the results of prior studies, which were restricted to idealized model systems and did not investigate the competition between the two effects.
- (4)
- The ab initio calculations well describe the energetically favored condition of Mn–C clustering and provide a theoretical explanation on an atomistic scale of the clustering formation and evolution in the X60Mn18 steel.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- De Cooman, B.C.; Estrin, Y.; Kim, S.K. Twinning-induced plasticity (TWIP) steels. Acta Mater. 2018, 142, 283–362. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C.P.; Cugy, P.; Barbier, D. High manganese austenitic twinning induced plasticity steels: A review of the microstructure properties relationships. Curr. Opin. Solid State Mater. Sci. 2011, 15, 141–168. [Google Scholar] [CrossRef]
- Yang, H.K.; Zhang, Z.J.; Dong, F.Y.; Duan, Q.Q.; Zhang, Z.F. Strain rate effects on tensile deformation behaviors for Fe–22Mn–0.6C–(1.5Al) twinning-induced plasticity steel. Mater. Sci. Eng. A 2014, 607, 551–558. [Google Scholar] [CrossRef]
- Chen, L.; Kim, H.-S.; Kim, S.-K.; De Cooman, B.C. Localized deformation due to Portevin-LeChatelier effect in 18Mn–0.6C TWIP austenitic Steel. ISIJ Int. 2007, 47, 1804–1812. [Google Scholar] [CrossRef]
- Güvenç, O.; Roters, F.; Hickel, T.; Bambach, M. ICME for crashworthiness of TWIP Steels: From ab initio to the crash performance. JOM 2015, 67, 120–128. [Google Scholar] [CrossRef]
- Bouaziz, O.; Zurob, H.; Huang, M. Driving force and logic of development of advanced high strength steels for automotive applications. Steel Res. Int. 2013, 84, 937–947. [Google Scholar] [CrossRef]
- Bleck, W.; Guo, X.; Ma, Y. The TRIP effect and its application in cold formable sheet steels. Steel Res. Int. 2017, 88, 1700218. [Google Scholar] [CrossRef]
- Kim, J.-K.; De Cooman, B.C. Stacking fault energy and deformation mechanisms in Fe–xMn–0.6C–yAl TWIP steel. Mater. Sci. Eng. A 2016, 676, 216–231. [Google Scholar] [CrossRef]
- Kang, M.; Shin, E.; Woo, W.; Lee, Y.-K. Small-angle neutron scattering analysis of Mn–C clusters in high-manganese 18Mn–0.6C steel. Mater. Charact. 2014, 96, 40–45. [Google Scholar] [CrossRef]
- Kim, J.; Estrin, Y.; De Cooman, B.C. Application of a dislocation density-based constitutive model to Al-alloyed TWIP steel. Metall. Mater. Trans. A 2013, 44, 4168–4182. [Google Scholar] [CrossRef]
- Jin, J.-E.; Lee, Y.-K. Effects of Al on microstructure and tensile properties of C-bearing high Mn TWIP steel. Acta Mater. 2012, 60, 1680–1688. [Google Scholar] [CrossRef]
- Jung, I.-C.; De Cooman, B.C. Temperature dependence of the flow stress of Fe–18Mn–0.6C–xAl twinning-induced plasticity steel. Acta Mater. 2013, 61, 6724–6735. [Google Scholar] [CrossRef]
- Lee, S.-J.; Kim, J.; Kane, S.N.; De Cooman, B.C. On the origin of dynamic strain aging in twinning-induced plasticity steels. Acta Mater. 2011, 59, 6809–6819. [Google Scholar] [CrossRef]
- Scott, C.; Allain, S.; Faral, M.; Guelton, N. The development of a new Fe–Mn–C austenitic steel for automotive applications. Metall. Res. Technol. 2006, 103, 293–302. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Raabe, D. Grain size effect on strain hardening in twinning-induced plasticity steels. Scr. Mater. 2012, 66, 992–996. [Google Scholar] [CrossRef]
- Kim, J.-K.; Chen, L.; Kim, H.-S.; Kim, S.-K.; Estrin, Y.; De Cooman, B.C. On the tensile behavior of high-manganese twinning-induced plasticity steel. Metall. Mater. Trans. A 2009, 40, 3147–3158. [Google Scholar] [CrossRef]
- Dastur, Y.N.; Leslie, W.C. Mechanism of work hardening in Hadfield manganese steel. Metall. Trans. A 1981, 12, 749–759. [Google Scholar] [CrossRef]
- Marceau, R.K.W.; Choi, P.; Raabe, D. Understanding the detection of carbon in austenitic high-Mn steel using atom probe tomography. Ultramicroscopy 2013, 132, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Hellman, O.C.; du Rivage, J.B.; Seidman, D.N. Efficient sampling for three-dimensional atom probe microscopy data. Ultramicroscopy 2003, 95, 199–205. [Google Scholar] [CrossRef]
- Svergun, D.I.; Koch, M.H.J. Small-angle scattering studies of biological macromolecules in solution. Rep. Prog. Phys. 2003, 66, 1735–1782. [Google Scholar] [CrossRef]
- Radulescu, A.; Mathers, R.T.; Coates, G.W.; Richter, D.; Fetters, L.J. A SANS study of the self-assembly in solution of syndiotactic polypropylene homopolymers, syndiotactic polypropylene-block-poly(ethylene-co-propylene) diblock copolymers, and an alternating atactic-isotactic multisegment polypropylene. Macromolecules 2004, 37, 6962–6971. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Fratini, E.; Baglioni, P.; Chen, W.-R.; Chen, S.-H. Effective long-range attraction between protein molecules in solutions studied by small angle neutron scattering. Phys. Rev. Lett. 2005, 95, 118102. [Google Scholar] [CrossRef] [PubMed]
- Bambach, M.D.; Bleck, W.; Kramer, H.S.; Klein, M.; Eifler, D.; Beck, T.; Surm, H.; Zoch, H.-W.; Hoffmann, F.; Radulescu, A. Tailoring the hardening behavior of 18CrNiMo7-6 via Cu alloying. Steel Res. Int. 2016, 87, 550–561. [Google Scholar] [CrossRef]
- Song, W.; Radulescu, A.; Liu, L.; Bleck, W. Study on a high entropy alloy by high energy synchrotron X-Ray diffraction and small angle neutron scattering. Steel Res. Int. 2017, 88, 1700079. [Google Scholar] [CrossRef]
- Radlinski, A.; Mastalerz, M.; Hinde, A.; Hainbuchner, M.; Rauch, H.; Baron, M.; Lin, J.; Fan, L.; Thiyagarajan, P. Application of SAXS and SANS in evaluation of porosity, pore size distribution and surface area of coal. Int. J. Coal Geol. 2004, 59, 245–271. [Google Scholar] [CrossRef]
- Feigin, L.A.; Svergun, D.I.; Taylor, G.W. Structure Analysis by Small-Angle X-Ray and Neutron Scattering; Plenum Press: New York, NY, USA, 1987; pp. 83–87. ISBN 9781475766264. [Google Scholar]
- Radulescu, A.; Szekely, N.K.; Appavou, M.-S. KWS-2: Small angle scattering diffractometer. J. Large-Scale Res. Facil. 2015, 1, 29. [Google Scholar] [CrossRef]
- Pedersen, J.S. Determination of size distribution from small-angle scattering data for systems with effective hard-sphere interactions. J. Appl. Crystallogr. 1994, 27, 595–608. [Google Scholar] [CrossRef]
- Von Appen, J.; Dronskowski, R. Carbon-induced ordering in manganese-rich austenite—A density-functional total-energy and chemical-bonding study. Steel Res. Int. 2011, 82, 101–107. [Google Scholar] [CrossRef]
- Timmerscheidt, T.A.; Dronskowski, R. An ab initio study of carbon-induced ordering in austenitic Fe–Mn–Al–C alloys. Steel Res. Int. 2017, 88, 1600292. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H. Carbon–carbon interactions in iron. J. Mater. Sci. 2004, 39, 3949–3955. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616–3621. [Google Scholar] [CrossRef]
- Zunger, A.; Wie, S.-H.; Ferreira, L.G.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef] [PubMed]
- Van de Walle, A.; Asta, M.; Ceder, G. The alloy theoretic automated toolkit: A user guide. Calphad 2002, 26, 539–553. [Google Scholar] [CrossRef]
- Van de Walle, A.; Tiwary, P.; De Jong, M.; Olmsted, D.L.; Asta, M.; Dick, A.; Shin, D.; Wang, Y.; Chen, L.-Q.; Liu, Z.-K. Efficient stochastic generation of special quasirandom structures. Calphad 2013, 42, 13–18. [Google Scholar] [CrossRef]
- Hafner, J. Ab-initio simulations of materials using VASP: Density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044–2078. [Google Scholar] [CrossRef] [PubMed]
- Gyorffy, B.L.; Pindor, A.J.; Staunton, J.; Stocks, G.M.; Winter, H. A first-principles theory of ferromagnetic phase transitions in metals. J. Phys. F Met. Phys. 1985, 15, 1337–1386. [Google Scholar] [CrossRef]
- Gonser, U.; Meechan, C.J.; Muir, A.H.; Wiedersich, H. Determination of Néel temperatures in fcc iron. J. Appl. Phys. 1963, 34, 2373–2378. [Google Scholar] [CrossRef]
- Rankin, D.W. CRC handbook of chemistry and physics, 89th edition, edited by David R. Lide. Crystallogr. Rev. 2009, 15, 223–224. [Google Scholar] [CrossRef]
- Dey, P.; Nazarov, R.; Dutta, B.; Yao, M.J.; Herbig, M.; Friák, M.; Hickel, T.; Raabe, D.; Neugebauer, J. Ab initio explanation of disorder and off-stoichiometry in Fe–Mn–Al–C κ carbides. Phys. Rev. B 2017, 95, 104108. [Google Scholar] [CrossRef]
- Breßler, I.; Kohlbrecher, J.; Thünemann, A.F. SASfit: A tool for small-angle scattering data analysis using a library of analytical expressions. J. Appl. Crystallogr. 2015, 48, 1587–1598. [Google Scholar] [CrossRef] [PubMed]
- Eck, B. wxDragon Version 2.1.0; RWTH Aachen: Aachen, Germany, 2016. [Google Scholar]
- Owen, W.S.; Grujicic, M. Strain aging of austenitic hadfield manganese steel. Acta Mater. 1999, 47, 111–126. [Google Scholar] [CrossRef]
- Saeed-Akbari, A.; Mosecker, L.; Schwedt, A.; Bleck, W. Characterization and prediction of flow behavior in high-manganese twinning induced plasticity steels: Part I. Mechanism Maps and Work-Hardening Behavior. Metall. Mater. Trans. A 2012, 43, 1688–1704. [Google Scholar] [CrossRef]
- Koyama, M.; Sawaguchi, T.; Lee, T.; Lee, C.S.; Tsuzaki, K. Work hardening associated with ε-martensitic transformation, deformation twinning and dynamic strain aging in Fe–17Mn–0.6C and Fe–17Mn–0.8C TWIP steels. Mater. Sci. Eng. A 2011, 528, 7310–7316. [Google Scholar] [CrossRef]
- Koyama, M.; Sawaguchi, T.; Tsuzaki, K. Influence of dislocation separation on dynamic strain aging in a Fe–Mn–C austenitic steel. Mater. Trans. 2012, 53, 546–552. [Google Scholar] [CrossRef]
- Renard, K.; Ryelandt, S.; Jacques, P.J. Characterisation of the Portevin-Le Châtelier effect affecting an austenitic TWIP steel based on digital image correlation. Mater. Sci. Eng. A 2010, 527, 2969–2977. [Google Scholar] [CrossRef]
- Koyama, M.; Sawaguchi, T.; Tsuzaki, K. TWIP effect and plastic instability condition in an Fe–Mn–C austenitic steel. ISIJ Int. 2013, 53, 323–329. [Google Scholar] [CrossRef]
- Shen, Y.F.; Jia, N.; Misra, R.; Zuo, L. Softening behavior by excessive twinning and adiabatic heating at high strain rate in a Fe–20Mn–0.6C TWIP steel. Acta Mater. 2016, 103, 229–242. [Google Scholar] [CrossRef]
- Lai, H.J.; Wan, C.M. The study of work hardening in Fe–Mn–Al–C alloys. J. Mater. Sci. 1989, 24, 2449–2453. [Google Scholar] [CrossRef]
- Wang, X.; Zurob, H.S.; Embury, J.D.; Ren, X.; Yakubtsov, I. Microstructural features controlling the deformation and recrystallization behaviour Fe–30% Mn and Fe–30% Mn–0.5% C. Mater. Sci. Eng. A 2010, 527, 3785–3791. [Google Scholar] [CrossRef]
- Song, W.; Ingendahl, T.; Bleck, W. Control of strain hardening behavior in high-Mn austenitic steels. Acta Metall. Sin. (Engl. Lett.) 2014, 27, 546–556. [Google Scholar] [CrossRef]
- Song, W. Mn-C short-range ordering and local deformation in a high-manganese steels. Mater. Sci. Eng. A 2018. in submission. [Google Scholar]
- Daamen, M.; Nessen, W.; Pinard, P.T.; Richter, S.; Schwedt, A.; Hirt, G. Deformation behavior of high-manganese TWIP steels produced by twin-roll strip casting. Procedia Eng. 2014, 81, 1535–1540. [Google Scholar] [CrossRef]
- Ma, Y.; Song, W.; Bleck, W. Investigation of the microstructure evolution in a Fe–17Mn–1.5Al–0.3C Steel via in situ synchrotron X-ray diffraction during a tensile test. Materials 2017, 10. [Google Scholar] [CrossRef]
- Shun, T.; Wan, C.M.; Byrne, J.G. A study of work hardening in austenitic Fe–Mn–C and Fe–Mn–Al–C alloys. Acta Metall. Mater. 1992, 40, 3407–3412. [Google Scholar] [CrossRef]
- Zuidema, B.K.; Subramanyam, D.K.; Leslie, W.C. The effect of aluminum on the work hardening and wear resistance of hadfield manganese steel. Metall. Trans. A 1987, 18, 1629–1639. [Google Scholar] [CrossRef]









| Element | C | Si | Mn | P | S | Cr | Ni | Al | Fe |
|---|---|---|---|---|---|---|---|---|---|
| wt % | 0.594 | 0.05 | 18.40 | 0.007 | 0.009 | 0.02 | 0.04 | 0.005 | Rest |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, W.; Bogdanovski, D.; Yildiz, A.B.; Houston, J.E.; Dronskowski, R.; Bleck, W. On the Mn–C Short-Range Ordering in a High-Strength High-Ductility Steel: Small Angle Neutron Scattering and Ab Initio Investigation. Metals 2018, 8, 44. https://doi.org/10.3390/met8010044
Song W, Bogdanovski D, Yildiz AB, Houston JE, Dronskowski R, Bleck W. On the Mn–C Short-Range Ordering in a High-Strength High-Ductility Steel: Small Angle Neutron Scattering and Ab Initio Investigation. Metals. 2018; 8(1):44. https://doi.org/10.3390/met8010044
Chicago/Turabian StyleSong, Wenwen, Dimitri Bogdanovski, Ahmet Bahadir Yildiz, Judith E. Houston, Richard Dronskowski, and Wolfgang Bleck. 2018. "On the Mn–C Short-Range Ordering in a High-Strength High-Ductility Steel: Small Angle Neutron Scattering and Ab Initio Investigation" Metals 8, no. 1: 44. https://doi.org/10.3390/met8010044
APA StyleSong, W., Bogdanovski, D., Yildiz, A. B., Houston, J. E., Dronskowski, R., & Bleck, W. (2018). On the Mn–C Short-Range Ordering in a High-Strength High-Ductility Steel: Small Angle Neutron Scattering and Ab Initio Investigation. Metals, 8(1), 44. https://doi.org/10.3390/met8010044