Effects of Openings and Axial Load Ratio on the Lateral Capacity of Steel-Fiber-Reinforced Concrete Shear Walls
Abstract
:1. Introduction
2. Finite Element Models Used in the Parametric Study
2.1. Tests Conducted by Huang [16]
2.2. SFRC Constitutive Law
2.2.1. Uniaxial Compression Stress-Strain Relationship
2.2.2. Uniaxial Tension Stress-Strain Relationship
2.3. Reinforcing Bars Constitutive Law
2.4. Finite Element Type and Mesh
2.5. Boundary Conditions and Load Application
3. Validation of the Finite Element Models and Numerical Analysis
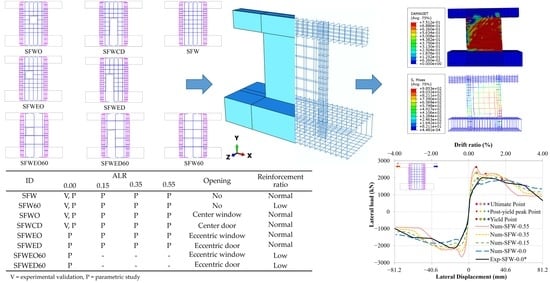
3.1. Specimens for the Parametric Study
Axial Load Ratio (ALR)
3.2. Classification of Failure Modes
- (1)
- Flexural failure modes can be divided into four damage levels:
- Undamaged (F0);
- With sub-horizontal flexural cracks (F1);
- With sub-horizontal flexural cracks and corner concrete crushing (F2);
- With sub-horizontal flexural cracks and base concrete crushing (F3).
- (2)
- Shear failure modes can be divided into four damage levels:
- Undamaged (S0);
- With diffused diagonal shear cracks (S1);
- With wide diagonal shear cracks (S2);
- With significant diagonal compression crushing (S3).
3.2.1. Specimen SFW (No Opening, Normal Reinforcement Ratio)
3.2.2. Specimen SFW60 (No Opening, Low Reinforcement Ratio)
3.2.3. Specimen SFWO (Center Window Opening, Normal Reinforcement Ratio)
3.2.4. Specimen SFWCD (Center Door Opening, Normal Reinforcement Ratio)
3.2.5. Specimen SFWEO (Eccentric Window Opening, Normal Reinforcement Ratio) and SFWEO60 (Eccentric Window Opening, Low Reinforcement Ratio)
3.2.6. Specimen SFWED (Eccentric Door Opening, Normal Reinforcement Ratio) and SFWED60 (Eccentric Door Opening, Low Reinforcement Ratio)
3.3. Estimate of Ductility
4. Conclusions
- A classification of the shear wall failure modes is proposed, where it is observed that, as ALR increases, the flexural-induced damage decreases, while the shear-induced damage increases, thus reducing both ductility and deformation capacity, as shown in the last section.
- As ALR increases, both lateral load capacity and stiffness increase and show a positive correlation with ALR while in the final post-peak stage, the relationship between lateral load capacity and ALRs is reversed, showing a negative correlation.
- Even in the presence of window or door openings, and with ALR up to 0.55, the specimens still show relatively good lateral load and deformation capacity, thanks to the improvement introduced by the SFRC.
- In general, window openings tend to reduce the lateral deformation capacity, while door openings tend to reduce the lateral load capacity. Therefore, if the lateral deformation capacity is of concern, window openings can be preferably obtained from door openings with a flexible infill at the bottom.
- In the case of eccentric openings, as the reinforcement ratio decreases, the difference in the lateral load capacity in opposite directions increases. This phenomenon is more significant with door than with window openings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, H.; Zhang, Y.; Lu, X.; Duan, Y.; Zhang, H. Influence of Axial Load Ratio on the Seismic Behavior of Steel Fiber–Reinforced Concrete Composite Shear Walls. J. Struct. Eng. 2020, 146, 04019171. [Google Scholar] [CrossRef]
- Alarcon, C.; Hube, M.; de la Llera, J. Effect of axial loads in the seismic behavior of reinforced concrete walls with unconfined wall boundaries. Eng. Struct. 2014, 73, 13–23. [Google Scholar] [CrossRef]
- Su, R.; Wong, S. Seismic behaviour of slender reinforced concrete shear walls under high axial load ratio. Eng. Struct. 2007, 29, 1957–1965. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Cao, W. Hysteretic behavior of high-strength concrete shear walls with high-strength steel bars: Experimental study and modelling. Eng. Struct. 2020, 214, 110600. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, Y.; Zhang, H.; Zhang, H.; Xiao, R. Experimental study on seismic performance of steel fiber reinforced high strength concrete composite shear walls with different steel fiber volume fractions. Eng. Struct. 2018, 171, 247–259. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Kheyroddin, A.; Mastali, M. An experimental investigation into the impacts of eccentric openings on the in-plane behavior of squat RC shear walls. Eng. Struct. 2019, 197, 109410. [Google Scholar] [CrossRef]
- Fattuhi, N.I. Strength of Sfrc Corbels Subjected to Vertical Load. J. Struct. Eng. Asce 1990, 116, 701–718. [Google Scholar] [CrossRef]
- Thomas, J.; Ramaswamy, A. Mechanical Properties of Steel Fiber-Reinforced Concrete. J. Mater. Civ. Eng. 2007, 19, 385–392. [Google Scholar] [CrossRef]
- Jayanth, K.; Prakash, M.N.S.; Suresh, G.S.; Naveen, B.O. Studies on the behaviour of steel fibre-reinforced concrete under monotonic and repeated cyclic stress in compression. Arch. Civ. Mech. Eng. 2022, 22, 50. [Google Scholar] [CrossRef]
- Shi, X.; Park, P.; Rew, Y.; Huang, K.; Sim, C. Constitutive behaviors of steel fiber reinforced concrete under uniaxial compression and tension. Constr. Build. Mater. 2020, 233, 117316. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Yi, W. Experimental Investigation on Stress Redistribution and Load-Transfer Paths of Shear Walls with Openings. J. Struct. Eng. 2018, 144, 04018149. [Google Scholar] [CrossRef]
- Popescu, C.; Sas, G.; Sabău, C.; Blanksvärd, T. Effect of Cut-Out Openings on the Axial Strength of Concrete Walls. J. Struct. Eng. 2016, 142, 04016100. [Google Scholar] [CrossRef]
- Massone, L.M.; Muñoz, G.; Rojas, F. Experimental and numerical cyclic response of RC walls with openings. Eng. Struct. 2019, 178, 318–330. [Google Scholar] [CrossRef]
- Wang, J.; Sakashita, M.; Kono, S.; Tanaka, H. Shear behaviour of reinforced concrete structural walls with eccentric openings under cyclic loading: Experimental study. Struct. Des. Tall Spec. Build. 2012, 21, 669–681. [Google Scholar] [CrossRef]
- Dashti, F.; Dhakal, R.P.; Pampanin, S. Validation of a Numerical Model for Prediction of Out-of-Plane Instability in Ductile Structural Walls under Concentric In-Plane Cyclic Loading. J. Struct. Eng. 2018, 144, 04018039. [Google Scholar] [CrossRef]
- Huang, C.-Y. The Study on Strength Prediction Model and Behavior of High Strength Steel Fiber Reinforced Concrete Walls with Opening. Master’s Thesis, Department of Civil Engineering College of Engineering, National Taiwan University, Taipei, Taiwan, 2022. Available online: https://drive.google.com/file/d/1wpbOPdxmzh0RWemd0QkI21TI6X7JLayG/view?usp=sharing (accessed on 10 August 2022).
- Ma, J.; Ning, C.-L.; Li, B. Peak Shear Strength of Flanged Reinforced Concrete Squat Walls. J. Struct. Eng. 2020, 146, 04020037. [Google Scholar] [CrossRef]
- Wei, F.; Chen, H.; Xie, Y. Experimental study on seismic behavior of reinforced concrete shear walls with low shear span ratio. J. Build. Eng. 2022, 45, 103602. [Google Scholar] [CrossRef]
- Fatemi, H.; Paultre, P.; Lamarche, C.-P. Evaluation of Inelastic Higher-Mode Effects on the Seismic Behavior of RC Structural Walls. J. Struct. Eng. 2020, 146, 04020016. [Google Scholar] [CrossRef] [Green Version]
- Alwashali, H.; Maeda, M.; Ogata, Y.; Aizawa, N.; Tsurugai, K. Residual seismic performance of damaged reinforced concrete walls. Eng. Struct. 2021, 243, 112673. [Google Scholar] [CrossRef]
- Rong, X.-L.; Zheng, S.-S.; Zhang, Y.-X.; Zhang, X.-Y.; Dong, L.-G. Experimental study on the seismic behavior of RC shear walls after freeze-thaw damage. Eng. Struct. 2020, 206, 110101. [Google Scholar] [CrossRef]
- Erbaş, Y.; Anıl, Ö.; Özdemir, A.; Kopraman, Y. Prediction of capacity of reinforced concrete shear wall with multiple openings by using nonlinear finite element analysis. Struct. Concr. 2022; Early view. [Google Scholar] [CrossRef]
- Kim, S.-H.; Lee, E.-K.; Kang, S.-M.; Park, H.-G.; Park, J.-H. Effect of boundary confinement on ductility of RC walls. Eng. Struct. 2021, 230, 111695. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, G.; Shu, Q.; Zhu, M.; Lu, L. Investigation on seismic behavior of RC shear walls with multiple post-construction openings based on experiment and simulation. J. Build. Eng. 2022, 46, 103707. [Google Scholar] [CrossRef]
- Yang, C.; Chou, Y.-C.; Hung, C.-C. Seismic behavior of full-scale wall piers with high-strength steel reinforcement. Eng. Struct. 2022, 256, 114068. [Google Scholar] [CrossRef]
- Barbachyn, S.M.; Devine, R.D.; Thrall, A.P.; Kurama, Y.C. Behavior of Nuclear RC Shear Walls Designed for Similar Lateral Strengths Using Normal-Strength versus High-Strength Materials. J. Struct. Eng. 2020, 146, 04020252. [Google Scholar] [CrossRef]
- Hung, C.-C.; Hsieh, P.-L. Comparative study on shear failure behavior of squat high-strength steel reinforced concrete shear walls with various high-strength concrete materials. Structures 2020, 23, 56–68. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Li, X.; Cao, W. Seismic behavior of steel fiber-reinforced high-strength concrete mid-rise shear walls with high-strength steel rebar. J. Build. Eng. 2021, 42, 102462. [Google Scholar] [CrossRef]
- Zhao, J.; Dun, H. A restoring force model for steel fiber reinforced concrete shear walls. Eng. Struct. 2014, 75, 469–476. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; Cao, W.; Zhu, Y. Seismic behavior of steel fiber reinforced high strength concrete shear walls with different embedded steel configurations. J. Build. Eng. 2022, 53, 104551. [Google Scholar] [CrossRef]
- Sakr, M.A.; El-Khoriby, S.R.; Khalifa, T.M.; Nagib, M.T. Modeling of RC shear walls strengthened with ultra-high performance fiber reinforced concrete (UHPFRC) jackets. Eng. Struct. 2019, 200, 109696. [Google Scholar] [CrossRef]
- Nagib, M.T.; Sakr, M.A.; El-Khoriby, S.R.; Khalifa, T.M. Cyclic behaviour of squat reinforced concrete shear walls strengthened with ultra-high performance fiber reinforced concrete. Eng. Struct. 2021, 246, 112999. [Google Scholar] [CrossRef]
- Hung, C.-C.; Li, H.; Chen, H.-C. High-strength steel reinforced squat UHPFRC shear walls: Cyclic behavior and design implications. Eng. Struct. 2017, 141, 59–74. [Google Scholar] [CrossRef]
- Kassem, W.; Elsheikh, A. Estimation of Shear Strength of Structural Shear Walls. J. Struct. Eng. 2010, 136, 1215–1224. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, Y.; Duan, Y.; Du, G. The V-MVLE model for cyclic failure behavior simulation of planar RC members. Thin-Walled Struct. 2022, 181, 110159. [Google Scholar] [CrossRef]
- Abdullah, S.A.; Wallace, J.W. Drift Capacity at Axial Failure of RC Structural Walls and Wall Piers. J. Struct. Eng. 2021, 147, 04021062. [Google Scholar] [CrossRef]
- Li, B.; Chi, Y.; Xu, L.; Li, C.; Shi, Y. Cyclic tensile behavior of SFRC: Experimental research and analytical model. Constr. Build. Mater. 2018, 190, 1236–1250. [Google Scholar] [CrossRef]
- Lee, S.C.; Oh, J.H.; Cho, J.Y. Compressive Behavior of Fiber-Reinforced Concrete with End-Hooked Steel Fibers. Materials 2015, 8, 1442–1458. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Fan, F.; Lai, J.; Xie, Y. Steel fiber reinforced concrete: A review of its material properties and usage in tunnel lining. Structures 2021, 34, 1080–1098. [Google Scholar] [CrossRef]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G.; Elenas, A. Effect of Steel Fibers on the Hysteretic Performance of Concrete Beams with Steel Reinforcement-Tests and Analysis. Materials 2020, 13, 2923. [Google Scholar] [CrossRef]
- Ravichandran, D.; Prem, P.R.; Kaliyavaradhan, S.K.; Ambily, P. Influence of fibers on fresh and hardened properties of Ultra High Performance Concrete (UHPC)—A review. J. Build. Eng. 2022, 57, 104922. [Google Scholar] [CrossRef]
- Li, B.; Prem, P.R.; Kaliyavaradhan, S.K.; Ambily, P. Experimental investigation on the stress-strain behavior of steel fiber reinforced concrete subjected to uniaxial cyclic compression. Constr. Build. Mater. 2017, 140, 109–118. [Google Scholar] [CrossRef]
- Deng, F.; Chi, Y.; Xu, L.; Huang, L.; Hu, X. Constitutive behavior of hybrid fiber reinforced concrete subject to uniaxial cyclic tension: Experimental study and analytical modeling. Constr. Build. Mater. 2021, 295, 123650. [Google Scholar] [CrossRef]
- dos Santos, L.R.; de Sousa Cardoso, H.; Caldas, R.B.; Grilo, L.F. Finite element model for bolted shear connectors in concrete-filled steel tubular columns. Eng. Struct. 2020, 203, 109863. [Google Scholar] [CrossRef]
- Li, W.; Han, L.-H. Seismic performance of CFST column to steel beam joints with RC slab: Analysis. J. Constr. Steel Res. 2011, 67, 127–139. [Google Scholar] [CrossRef]
- Fang, C.; Ali, M.S.M.; Sheikh, A.H.; Singh, M. Numerical and Finite-Element Analysis of Short Ultrahigh-Performance Fiber-Reinforced Concrete Columns. J. Struct. Eng. 2019, 145, 04019111. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Tan, J.; Vandevyvere, B. Nonlinear finite-element analysis for hysteretic behavior of ECC-encased CFST columns. Structures 2020, 25, 670–682. [Google Scholar] [CrossRef]
- Bonilla, J.; Bezerra, L.M.; Mirambell, E. Resistance of stud shear connectors in composite beams using profiled steel sheeting. Eng. Struct. 2019, 187, 478–489. [Google Scholar] [CrossRef]
- Abouali, S.; Shahverdi, M.; Ghassemieh, M.; Motavalli, M. Nonlinear simulation of reinforced concrete beams retrofitted by near-surface mounted iron-based shape memory alloys. Eng. Struct. 2019, 187, 133–148. [Google Scholar] [CrossRef]
- Raza, A.; Khan, Q.u.Z.; Ahmad, A. Investigation of HFRC columns reinforced with GFRP bars and spirals under concentric and eccentric loadings. Eng. Struct. 2021, 227, 111461. [Google Scholar] [CrossRef]
- Paulay, T.; Priestly, M.J.N. Seismic Design of Reinforced Concrete and Masonry Buildings, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Zhang, H.Y.; Cheng, X.; Li, Y.; Du, X. Prediction of failure modes, strength, and deformation capacity of RC shear walls through machine learning. J. Build. Eng. 2022, 50, 104145. [Google Scholar] [CrossRef]

























| Ref | Concrete Type | Exp | Num | Equ | ALR Computed According to | Openings | |||
|---|---|---|---|---|---|---|---|---|---|
| Equation (20) | Equation (21) | No | Win | Door | |||||
| [17] | RC | √ | √ | √ | |||||
| [18] | RC | √ | √ | −0.1, 0.3, 0.5 | - | √ | |||
| [19] | RC | √ | √ | 0.03 | 0.06 | √ | |||
| [20] | RC | √ | √ | 0.013, 0.016, 0.013 | 0.039, 0.049, 0.029 | √ | |||
| [21] | RC | √ | √ | 0.1, 0.2, 0.3 | - | √ | |||
| [22] | RC | √ | √ | 0.0 | √ | √ | √ | ||
| [23] | RC | √ | 0.15 | - | √ | ||||
| [6] | RC | √ | 0.0 | √ | √ | ||||
| [24] | RC | √ | √ | 0.1 | - | √ | √ | ||
| [25] | RC | √ | 0.08, 0.13 | - | √ | ||||
| [26] | RC | √ | 0.0 | √ | |||||
| [11] | RC | √ | √ | 0.090, 0.092 | - | √ | √ | ||
| [13] | RC | √ | √ | 0.07 | - | √ | |||
| [12] | RC | √ | - | √ | √ | ||||
| [2] | RC | √ | 0.15, 0.25, 0.35 | - | √ | ||||
| [4] | RC, SFRC | √ | √ | - | 0.4, 0.6 | √ | |||
| [27] | RC, SFRC | √ | √ | 0.0 | √ | ||||
| [28] | RC, SFRC | √ | √ | - | 0.3 | √ | |||
| [29] | SFRC | √ | √ | 0.1 | - | √ | |||
| [16] | SFRC | √ | √ | 0.0 | √ | √ | √ | ||
| [30] | SFRHSC | √ | √ | - | 0.2, 0.6, 0.8 | √ | |||
| [31] | UHPFRC | √ | 0.0 | √ | |||||
| [32] | UHPFRC | √ | √ | 0.1 | - | √ | |||
| [33] | UHPFRC | √ | √ | 0.0 | √ | ||||
| [34] | RC | √ | √ | √ | |||||
| [35] | RC | √ | √ | √ | |||||
| [36] | RC | √ | √ | √ | |||||
| Cylindrical compressive strength, | 65.7 MPa |
| Volume fraction of the fiber, | 1.5% |
| Length of the fiber, | 30 mm |
| Diameter of the fiber, | 0.38 mm |
| Tensile strength of the fiber | 2300 MPa |
| ID | Diameter (mm) | Area (mm2) | Yield Strength (MPa) | Yield Strain | Elastic Modulus (GPa) | Ultimate Tensile Strength (Mpa) | Ultimate Tensile Strain |
|---|---|---|---|---|---|---|---|
| 4 | 12.7 | 126.7 | 858 | 0.0039 | 220 | 1034 | 0.04 |
| 5 | 15.9 | 198.5 | 826 | 0.0038 | 217 | 1016 | 0.04 |
| 6 | 19.1 | 286.5 | 471 | 0.0024 | 196 | 696 | 0.04 |
| Dilation angle, | 30 |
| Eccentricity, | 0.1 |
| Stress ratio, | 1.16 |
| Shape of the yielding surface, | 0.6667 |
| Viscosity coefficient, μ | 0.001 |
| Concrete Grid (mm) | Computational Time (min) |
|---|---|
| 40 | 104 |
| 50 | 85 |
| 70 | 67 |
| ID | Concrete FE Type | Reinforcing Bars FE Type | Concrete Grid (mm) | Steel Bars Grid (mm) |
|---|---|---|---|---|
| Top Beam | C3D8R | T3D2 | 200 | 100 |
| Wall | C3D8R | T3D2 | 50 | 50 |
| Base beam | C3D8R | T3D2 | 200 | 100 |
| Disp (mm) | Drift (%) (=Disp/2030 mm) |
|---|---|
| 2.54 | 0.125 |
| 5.08 | 0.25 |
| 7.61 | 0.375 |
| 10.15 | 0.5 |
| 15.23 | 0.75 |
| 20.30 | 1 |
| 30.45 | 1.5 |
| 40.60 | 2 |
| 60.90 | 3 |
| 81.20 | 4 |
| ID | ALR | Opening | Reinforcement Ratio | |||
|---|---|---|---|---|---|---|
| 0.00 | 0.15 | 0.35 | 0.55 | |||
| SFW | V, P | P | P | P | No | Normal |
| SFW60 | V, P | P | P | P | No | Low |
| SFWO | V, P | P | P | P | Center window | Normal |
| SFWCD | V, P | P | P | P | Center door | Normal |
| SFWEO | P | P | P | P | Eccentric window | Normal |
| SFWED | P | P | P | P | Eccentric door | Normal |
| SFWEO60 | P | - | - | - | Eccentric window | Low |
| SFWED60 | P | - | - | - | Eccentric door | Low |
| ALR | (MPa) | (mm2) | (kN) |
|---|---|---|---|
| 0.0 | 65.7 | 120,000 | 0 |
| 0.15 | 65.7 | 120,000 | 1183 |
| 0.35 | 65.7 | 120,000 | 2759 |
| 0.55 | 65.7 | 120,000 | 4336 |
| Flexure-Induced Damage Levels | |||||
|---|---|---|---|---|---|
| F0 | F1 | F2 | F3 | ||
| Shear-Induced Damage Levels | S0 |  |  |  |  |
| S1 |  |  |  |  | |
| S2 |  |  |  | None | |
| S3 |  |  |  | None | |
| Strain Distribution | |||
|---|---|---|---|
| ALR = 0.0 |  |  |  |
| ALR = 0.55 |  |  |  |
| Strain Distribution | |||
|---|---|---|---|
| ALR = 0.0 |  |  |  |
| ALR = 0.55 |  |  |  |
| Strain Distribution | |||
|---|---|---|---|
| ALR = 0.0 |  |  |  |
| ALR = 0.55 |  |  |  |
| Strain Distribution | |||
|---|---|---|---|
| ALR = 0.0 |  |  |  |
| ALR = 0.55 |  |  |  |
| Strain Distribution | |||
|---|---|---|---|
| ALR = 0.0 Force (+) |  |  |  |
| ALR = 0.55 Force (+) |  |  |  |
| ALR = 0.0 Force (−) |  |  |  |
| ALR = 0.55 Force (−) |  |  |  |
| Strain Distribution | |||
|---|---|---|---|
| ALR = 0.0 Force (+) |  |  |  |
| ALR = 0.55 Force (+) |  |  |  |
| ALR = 0.0 Force (−) |  |  |  |
| ALR = 0.55 Force (−) |  |  |  |
| ID | Force Direction | ALR | Yield Point | Post-Yield Peak Point | Ultimate Point | Ductility Index | |||
|---|---|---|---|---|---|---|---|---|---|
| Drift Ratio at Yield (%) | Yield Force (MN) | Drift Ratio at Post-Yield Peak (%) | Post-Yield Peak Force (MN) | Drift Ratio at Ultimate (%) | 85% of Post-Yield Peak Force (MN) | ||||
| SFW | (+), (−) | 0 | 0.50 | 1.70 | 1.90 | 1.80 | 3.10 | 1.53 | 6.2 |
| 0.15 | 0.48 | 2.00 | 1.55 | 2.05 | 2.40 | 1.74 | 5.0 | ||
| 0.35 | 0.42 | 2.30 | 1.00 | 2.20 | 2.05 | 1.87 | 4.9 | ||
| 0.55 | 0.39 | 2.70 | 0.90 | 2.30 | 1.70 | 1.96 | 4.4 | ||
| SFW60 | (+), (−) | 0 | 0.53 | 1.70 | 1.70 | 1.60 | 3.70 | 1.36 | 7.0 |
| 0.15 | 0.48 | 2.00 | 1.40 | 1.70 | 2.40 | 1.45 | 5.0 | ||
| 0.35 | 0.43 | 2.30 | 1.00 | 1.90 | 2.00 | 1.62 | 4.7 | ||
| 0.55 | 0.40 | 2.70 | 0.80 | 2.00 | 1.60 | 1.70 | 4.0 | ||
| SFWO | (+), (−) | 0 | 0.40 | 1.20 | 1.40 | 1.50 | 4.00 | 1.28 | 10.0 |
| 0.15 | 0.35 | 1.40 | 1.10 | 1.60 | 1.90 | 1.36 | 5.4 | ||
| 0.35 | 0.30 | 1.60 | 0.80 | 1.70 | 1.45 | 1.45 | 4.8 | ||
| 0.55 | 0.30 | 1.80 | 0.60 | 1.80 | 1.40 | 1.53 | 4.7 | ||
| SFWEO | (+) | 0 | 0.30 | 1.00 | 0.80 | 1.35 | 3.40 | 1.15 | 11.3 |
| 0.15 | 0.23 | 1.25 | 0.75 | 1.50 | 2.50 | 1.28 | 10.9 | ||
| 0.35 | 0.25 | 1.55 | 0.73 | 1.70 | 1.50 | 1.45 | 6.0 | ||
| 0.55 | 0.30 | 1.80 | 0.70 | 1.80 | 1.50 | 1.53 | 5.0 | ||
| (−) | 0 | −0.40 | −1.20 | −0.90 | −1.40 | −3.20 | −1.19 | 8.0 | |
| 0.15 | −0.35 | −1.40 | −0.80 | −1.60 | −1.90 | −1.36 | 5.4 | ||
| 0.35 | −0.33 | −1.70 | −0.75 | −1.70 | −1.45 | −1.45 | 4.4 | ||
| 0.55 | −0.35 | −1.95 | −0.70 | −1.80 | −1.15 | −1.53 | 3.3 | ||
| SFWCD | (+), (−) | 0 | 0.35 | 0.90 | 1.30 | 1.20 | 3.00 | 1.02 | 8.6 |
| 0.15 | 0.30 | 1.20 | 0.90 | 1.35 | 2.20 | 1.15 | 7.3 | ||
| 0.35 | 0.30 | 1.45 | 0.80 | 1.55 | 1.60 | 1.32 | 5.3 | ||
| 0.55 | 0.35 | 1.70 | 0.60 | 1.70 | 1.55 | 1.45 | 4.4 | ||
| SFWED | (+) | 0 | 0.45 | 0.90 | 2.00 | 1.30 | 4.00 | 1.11 | 8.9 |
| 0.15 | 0.40 | 1.20 | 1.70 | 1.40 | 3.80 | 1.19 | 9.5 | ||
| 0.35 | 0.38 | 1.40 | 1.00 | 1.50 | 2.60 | 1.28 | 6.8 | ||
| 0.55 | 0.35 | 1.60 | 0.70 | 1.60 | 2.30 | 1.36 | 6.6 | ||
| (−) | 0 | −0.60 | −1.20 | −1.20 | −1.25 | −2.80 | −1.06 | 4.7 | |
| 0.15 | −0.40 | −1.44 | −0.80 | −1.44 | −1.80 | −1.22 | 4.5 | ||
| 0.35 | −0.35 | −1.60 | −0.80 | −1.60 | −1.55 | −1.36 | 4.4 | ||
| 0.55 | −0.35 | −1.80 | −0.95 | −1.70 | −1.35 | −1.45 | 3.9 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Zhang, H.; Monti, G.; Castoro, C. Effects of Openings and Axial Load Ratio on the Lateral Capacity of Steel-Fiber-Reinforced Concrete Shear Walls. Buildings 2022, 12, 2032. https://doi.org/10.3390/buildings12112032
Lin Z, Zhang H, Monti G, Castoro C. Effects of Openings and Axial Load Ratio on the Lateral Capacity of Steel-Fiber-Reinforced Concrete Shear Walls. Buildings. 2022; 12(11):2032. https://doi.org/10.3390/buildings12112032
Chicago/Turabian StyleLin, Zhou, Hongmei Zhang, Giorgio Monti, and Chiara Castoro. 2022. "Effects of Openings and Axial Load Ratio on the Lateral Capacity of Steel-Fiber-Reinforced Concrete Shear Walls" Buildings 12, no. 11: 2032. https://doi.org/10.3390/buildings12112032
APA StyleLin, Z., Zhang, H., Monti, G., & Castoro, C. (2022). Effects of Openings and Axial Load Ratio on the Lateral Capacity of Steel-Fiber-Reinforced Concrete Shear Walls. Buildings, 12(11), 2032. https://doi.org/10.3390/buildings12112032