Structural Landmark Salience Computation in Compact Urban Districts with 3D Node-Landmark Grid Analysis Model: A Case Study on Two Sample Districts in Changsha, China
Abstract
:1. Introduction
2. Literature Review
2.1. Grid Analysis Model Based on the Principle of Space Syntax
- Investigating as to how the logical space expresses the real space of the city;
- Establishing links between spatial nodes.
2.2. The Representation of 3D Isovist
3. Materials and Methods
3.1. 3D Isovist-Based Landmark Visibility Measurement Method
- No obstacle line-of-sight: the initially set viewing range is maintained, representing the visibility of the sky;
- Ground line-of-sight: line-of-sight projected onto the ground;
- Obstructive line-of-sight: line-of-sight is obstructed by geometry. At the same time, the reference number and length of the line-of-sight, as well as the reference number of the geometry onto which the line-of-sight is projected, are recorded in the 3D isovist dataset.
3.2. Simulation Model of a Standard Urban Neighborhood
- Natural landscape resources: mountains, forests, rivers, lakes, etc., within the city;
- Neighborhood blocks: urban residential area units made up of residential building groups;
- Public buildings: civic buildings of various functional types, including office buildings, shopping malls, hotels, conference centers, etc.
- Urban public facilities: streets, sidewalks, street trees, parks, squares, parking lots, etc.
3.3. Determination of Path Decision Nodes in 3D Grid
- The trees on either side of the trail were spaced 8 m apart and had a net height of more than 2.8 m below the branches of the canopy;
- The pavement trees were spaced 6 m apart, with a net height of more than 1.8 m below the crown branches;
- The line-of-sight triangle was set at the intersection.
- The height of the walking viewpoint was 1.6 m from the ground, the distance between the viewpoints was 30 m, and the playing speed of the dynamic snapshot corresponded to the walking speed of the person, which was 5 km/h;
- The riding viewpoint was 1.75 m from the ground height, the viewpoint spacing was 30 m, and the playback speed of the dynamic snapshot corresponded to the riding speed, 10 km/h;
- The driving viewpoint height from the ground was 1.35m, the viewpoint spacing was 50 m, and the playback speed of the dynamic snapshot corresponded to the speed of the motor vehicle, 20 km/h.
- Street intersections and street turns within the analysis area are decision nodes of the 3D grid;
- For arc roads, consecutive decision nodes should be set and the maximum spacing requirement should be satisfied;
- For roads with significant slopes, the decision node should be set at the top of the slope;
- When two roads intersect, path continuity can only be formed by secondary roads.
3.4. Expression Functions for Landmark Visibility in 3D Grid
4. Salience Computation of Structural Landmarks in Urban Neighborhood
4.1. Computation of Structural Landmark Salience
4.2. Computation Procedure of Structual Landmark Salience for Two Typical Samples of Districts in Changsha
- TP-District, an area typically formed by a combination of high- and low-rise architectural groups;
- XD-District, a typical area pattern formed mainly by high-rise building groups; the height of the proposed A2-Beichen Landmark was 268 m (Figure 11a), with Ha2 = 268 m as the default in the later text;
- For the XD-District, the height of the proposed A2-Beichen Landmark was set at 400 m (Figure 11b), with Ha2 = 400 m as the default in the latter part of the text.
5. Results
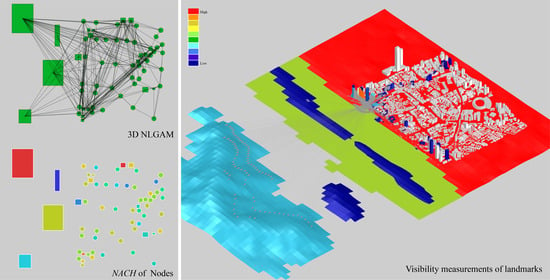
5.1. Spatial Movement Properties of 3D NL GAM
5.2. Structural Salience of Landmarks
6. Discussion
6.1. Correlation between Structural Landmark Salience and Urban Intellibility
6.2. The Significance of Computing the Structural Salience of Landmarks for Urban Design
6.3. Further Research Objectives
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saaty, T.; De Paola, P. Rethinking Design and Urban Planning for the Cities of the Future. Buildings 2017, 7, 76. [Google Scholar] [CrossRef]
- Secretariat, H.I. New Urban Agenda; United Nations: New York, NY, USA, 2017. [Google Scholar]
- Showkatbakhsh, M.; Makki, M. Multi-Objective Optimisation of Urban Form: A Framework for Selecting the Optimal Solution. Buildings 2022, 12, 1473. [Google Scholar] [CrossRef]
- Programme, U.P.F.G.; Office, U.H.F.U. SDG Project Assessment Tool Vol1: General Framework; United Nations Human Settlements Programme: Nairobi, Kenya, 2020; p. 13. Available online: https://unhabitat.org/sites/default/files/2020/07/sdg_tool_general_framework_jan_2020.pdf (accessed on 2 November 2022).
- Carmona, M.; Tiesdell, S.; Heath, T.; Oc, T. Public Places—Urban Spaces: The Dimensions of Urban Design, 2nd ed.; Architectural Press of Elsevier: Burlington, MA, USA, 2010. [Google Scholar]
- Rapoport, A. Toward a Redefinition of Density. Environ. Behav. 1975, 7, 133–158. [Google Scholar] [CrossRef]
- Fisher-Gewirtzman, D.; Wagner, I.A. Spatial Openness as a Practical Metric for Evaluating Built-up Environments. Environ. Plan. B Plan. Des. 2003, 30, 37–49. [Google Scholar] [CrossRef]
- Fisher-Gewirtzman, D. The association between perceived density in minimum apartments and spatial openness index three-dimensional visual analysis. Environ. Plan. B Urban Anal. City Sci. 2017, 44, 764–795. [Google Scholar] [CrossRef]
- Dalton, R.C.; Bafna, S. The syntactical image of the city: A reciprocal definition of spatial elements and spatial syntaxes. In Proceedings of the 4th International Space Syntax Symposium, London, UK, 17–19 June 2003. [Google Scholar]
- Stamps, A.E. Mystery, complexity, legibility and coherence: A meta-analysis. J. Environ. Psychol. 2004, 24, 1–16. [Google Scholar] [CrossRef]
- Lynch, K. The Image of the City; The MIT Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Claramunt, C.; Winter, S. Structural Salience of Elements of the City. Environ. Plan. B Plan. Des. 2007, 34, 1030–1050. [Google Scholar] [CrossRef]
- Sorrows, M.E.; Hirtle, S.C. The Nature of Landmarks for Real and Electronic Spaces; Springer: Berlin/Heidelberg, Germany, 1999; pp. 37–50. [Google Scholar]
- Caduff, D.; Timpf, S. On the assessment of landmark salience for human navigation. Cogn. Process. 2008, 9, 249–267. [Google Scholar] [CrossRef] [PubMed]
- Steck, S.D.; Mallot, H.A. The Role of Global and Local Landmarks in Virtual Environment Navigation. Presence Teleoperators Virtual Environ. 2000, 9, 69–83. [Google Scholar] [CrossRef]
- Röser, F.; Hamburger, K.; Krumnack, A.; Knauff, M. The structural salience of landmarks: Results from an on-line study and a virtual environment experiment. J. Spat. Sci. 2012, 57, 37–50. [Google Scholar] [CrossRef]
- Caduff, D.; Timpf, S. The Landmark Spider: Representing Landmark Knowledge for Wayfinding Tasks, 2005 AAAI Spring Symposium; Stanford: San Jose, CA, USA, 2005. [Google Scholar]
- Nuhn, E.; König, F.; Timpf, S. “Landmark Route”: A Comparison to the Shortest Route. AGILE GIScience Ser. 2022, 3, 12. [Google Scholar] [CrossRef]
- Filomena, G.; Verstegen, J.A. Modelling the effect of landmarks on pedestrian dynamics in urban environments. Comput. Environ. Urban Syst. 2021, 86, 101573. [Google Scholar] [CrossRef]
- Yesiltepe, D.; Dalton, R.; Ozbil, A.; Dalton, N.; Noble, S.; Hornberger, M.; Coutrot, A.; Spiers, H. Usage of landmarks in virtual environments for wayfinding: Research on the influence of global landmarks. In Proceedings of the 12th Space Syntax Symposium, Beijing, China, 8–13 July 2019. [Google Scholar]
- Ruddle, R.A.; Volkova, E.; Mohler, B.; Bülthoff, H.H. The effect of landmark and body-based sensory information on route knowledge. Mem. Cogn. 2011, 39, 686–699. [Google Scholar] [CrossRef]
- Kuipers, B. Modeling Spatial Knowledge. Cogn. Sci. 1978, 2, 129–153. [Google Scholar] [CrossRef]
- Yesiltepe, D.; Conroy Dalton, R.; Ozbil Torun, A. Landmarks in wayfinding: A review of the existing literature. Cogn. Process. 2021, 22, 369–410. [Google Scholar] [CrossRef]
- Richter, K.; Winter, S. Landmarks: GIScience for Intelligent Services; Springer International Publishing: Cham, Switzerland; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2014. [Google Scholar]
- Fischer, L.F.; Mojica Soto-Albors, R.; Buck, F.; Harnett, M.T. Representation of visual landmarks in retrosplenial cortex. Elife 2020, 9, e51458. [Google Scholar] [CrossRef] [PubMed]
- Klippel, A.; Winter, S. Structural Salience of Landmarks for Route Directions; Springer: Berlin/Heidelberg, Germany, 2005; pp. 347–362. [Google Scholar]
- Winter, S. Route adaptive selection of salient features. In Spatial Information Theory, Lecture Notes in Computer Science; Kuhn, W., Worboys, M., Timpf, S., Eds.; Springer: New York, NY, USA, 2003; pp. 349–361. [Google Scholar]
- Appleyard, D. Why Buildings Are Known: A Predictive Tool for Architects and Planners. Environ. Behav. 1969, 1, 131–156. [Google Scholar] [CrossRef]
- Hillier, B. Space is the Machine, Electronic ed.; Space Syntax: London, UK, 2007. [Google Scholar]
- Ostwald, M.J. The Mathematics of Spatial Configuration: Revisiting, Revising and Critiquing Justified Plan Graph Theory. Nexus Netw. J. 2011, 13, 445–470. [Google Scholar] [CrossRef]
- Morello, E.; Ratti, C. A digital image of the city: 3D isovists in Lynch’s urban analysis. Environ. Plan. B Plan. Des. 2009, 36, 837–853. [Google Scholar] [CrossRef]
- Kim, G.; Kim, A.; Kim, Y. A new 3D space syntax metric based on 3D isovist capture in urban space using remote sensing technology. Comput. Environ. Urban Syst. 2019, 74, 74–87. [Google Scholar] [CrossRef]
- Morais, F.; Vaz, J.; Viana, D.L.; Carvalho, I.C. 3D Space Syntax Analysis—Case Study ‘Casa da Música’. In Proceedings of the 11th Space Syntax Symposium, Lisbon, Portugal, 3–7 July 2017. [Google Scholar]
- Ascensão, A.; Costa, L.; Fernandes, C.; Morais, F. 3D Space Syntax Analysis: Attributes to be Applied in Landscape Architecture Projects. Urban Sci. 2019, 3, 20. [Google Scholar] [CrossRef]
- Dalton, R.C.; Dalton, N.S. The problem of representation of 3D isovists. In Proceedings of the 10th International Space Syntax Symposium, London, UK, 13–17 July 2015. [Google Scholar]
- Tara, A.; Lawson, G.; Renata, A. Measuring magnitude of change by high-rise buildings in visual amenity conflicts in Brisbane. Landsc. Urban Plan. 2021, 205, 103930. [Google Scholar] [CrossRef]
- Karimi, K. A configurational approach to analytical urban design: ‘Space syntax’ methodology. Urban Des. Int. 2012, 17, 297–318. [Google Scholar] [CrossRef]
- Yamu, C.; van Nes, A.; Garau, C. Bill Hillier’s Legacy: Space Syntax—A Synopsis of Basic Concepts, Measures, and Empirical Application. Sustainability 2021, 13, 3394. [Google Scholar] [CrossRef]
- Hiller, B.; Leaman, A. The man-environment paradigm and its paradoxes. Arch. Des. 1973, 78, 507–511. [Google Scholar]
- Karimi, K. Space syntax: Consolidation and transformation of an urban research field. J. Urban Des. 2018, 23, 1–4. [Google Scholar] [CrossRef]
- Batty, M. The New Science of Cities; The MIT Press: Cambridge, MA, USA; London, UK, 2013. [Google Scholar]
- Natapov, A.; Fisher-Gewirtzman, D. Visibility of urban activities and pedestrian routes: An experiment in a virtual environment. Comput. Environ. Urban Syst. 2016, 58, 60–70. [Google Scholar] [CrossRef]
- Alkamali, N.; Alhadhrami, N.; Alalouch, C. Muscat City Expansion and Accessibility to the Historical Core: Space Syntax Analysis. Energy Procedia 2017, 115, 480–486. [Google Scholar] [CrossRef]
- Koohsari, M.J.; Oka, K.; Owen, N.; Sugiyama, T. Natural movement: A space syntax theory linking urban form and function with walking for transport. Health Place 2019, 58, 102072. [Google Scholar] [CrossRef]
- Shen, Y.; Karimi, K. Urban evolution as a spatio-functional interaction process: The case of central Shanghai. J. Urban Des. 2018, 23, 42–70. [Google Scholar] [CrossRef]
- Liao, P.; Yu, R.; Gu, N.; Soltani, S. A Syntactical Spatio-Functional Analysis of Four Typical Historic Chinese Towns from a Heritage Tourism Perspective. Land 2022, 11, 2181. [Google Scholar] [CrossRef]
- Bill Hiller, J.H. The Social Logic of Space; Cambridge University Press: New York, NY, USA, 1984. [Google Scholar]
- Turner, A.; Penn, A.; Hillier, B. An Algorithmic Definition of the Axial Map. Environ. Plan. B Plan. Des. 2005, 32, 425–444. [Google Scholar] [CrossRef]
- Varoudis, T.; Penn, A. Visibility, accessibility and beyond: Next generation visibility graph analysis. In Proceedings of the 10th International Space Syntax Symposium, London, UK, 13–17 July 2015. [Google Scholar]
- Lee, J.H.; Ostwald, M.J.; Lee, H. Measuring the spatial and social characteristics of the architectural plans of aged care facilities. Front. Archit. Res. 2017, 6, 431–441. [Google Scholar] [CrossRef]
- Hillier, B.; Iida, S. Network and Psychological Effects in Urban Movement; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3693, pp. 475–490. [Google Scholar]
- Hillier, B. The architectures of seeing and going: Or, are cities shaped by bodies or minds? And is there a syntax of spatial cognition? In Proceedings of the 4th International Space Syntax Symposium, London, UK, 17–19 June 2003. [Google Scholar]
- van Nes, A.; Yamu, C. Introduction to Space Syntax in Urban Studies; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Benedikt, M.L. To take hold of space: Isovists and isovist fields. Environ. Plan. B Plan. Des. 1979, 6, 47–65. [Google Scholar] [CrossRef]
- Batty, M. Exploring Isovist Fields: Space and Shape in Architectural and Urban Morphology. Environ. Plan. B Plan. Des. 2001, 28, 123–150. [Google Scholar] [CrossRef]
- Batty, M.; Rana, S. The Automatic Definition and Generation of Axial Lines and Axial Maps. Environ. Plan. B Plan. Des. 2003, 31, 615–640. [Google Scholar] [CrossRef]
- Zolfagharkhani, M.; Ostwald, M.J. The Spatial Structure of Yazd Courtyard Houses: A Space Syntax Analysis of the Topological Characteristics of the Courtyard. Buildings 2021, 11, 262. [Google Scholar] [CrossRef]
- Hillier, B.; Yang, T.; Turner, A. Normalising least angle choice in Depthmap and how it opens up new perspectives on the global and local. J. Space Syntax 2012, 3, 155–193. [Google Scholar]
- Yang, T.; Li, M.; Shen, Z. Between morphology and function: How syntactic centers of the Beijing city are defined. J. Urban Manag. 2015, 4, 125–134. [Google Scholar] [CrossRef]
- Turner, A. Depthmap-a program to perform visibility graph analysis. In Proceedings of the 3rd International Space Syntax Symposium, Atlanta, GA, USA, 7–11 May 2001. [Google Scholar]
- Pinelo, J.; Turner, A. Introduction to UCL Depthmap 10 Version 10.08.00r; UCL Press: London, UK, 2010. [Google Scholar]
- Abdulmawla, A.; Bielik, M.; Buš, P.; Chang, M.-C.; Dennemark, M.; Fuchkina, E.; Miao, Y.; Knecht, K.; Koenig, R.; Schneider, S. DeCodingSpaces Toolbox for Grasshopper: Computational Analysis and Generation of STREET NETWORK, PLOTS and BUILDINGS. Available online: https://kar.kent.ac.uk/id/eprint/68953 (accessed on 10 April 2023).
- Natapov, A.; Czamanski, D.; Fisher-Gewirtzman, D. Can visibility predict location? Visibility graph of food and drink facilities in the city. Surv. Rev. 2013, 45, 462–471. [Google Scholar] [CrossRef]
- Natapov, A.; Fisher-Gewirtzman, D. Cities as Visuospatial Networks. In Smart City Networks; Rassia, S.T., Pardalos, M., Eds.; Springer: Cham, Switzerland, 2017; pp. 191–205. [Google Scholar]
- Bielik, M.; König, R.; Fuchkina, E.; Schneider, S.; Abdulmawla, A. Evolving Configurational Properties: Simulating multiplier effects between land use and movement patterns. In Proceedings of the 12th Space Syntax Symposium, Beijing, China, 8–13 July 2019. [Google Scholar]
- Hillier, B. Cities as movement economies. Urban Des. Int. 1996, 1, 41–60. [Google Scholar] [CrossRef]
- Hillier, B.; Penn, A.; Hanson, J.; Ki, T.G.; Xu, J. Natural movement: Or, configuration and attraction in urban pedestrian movement. Environ. Plan. B Plan. Des. 1993, 20, 29–66. [Google Scholar] [CrossRef]
- Nuhn, E.; Timpf, S. Do people prefer a landmark route over a shortest route? Cartogr. Geogr. Inf. Sci. 2022, 49, 407–425. [Google Scholar] [CrossRef]
- Nuhn, E.; Timpf, S. Landmark weights—An alternative to spatial distances in shortest route algorithms. Spat. Cogn. Comput. 2022; 1–27, ahead-of-print. [Google Scholar] [CrossRef]
- De Floriani, L.; Marzano, P.; Puppo, E. Line-of-Sight Communication on Terrain Models. Geogr. Inf. Syst. 1994, 8, 329–342. [Google Scholar] [CrossRef]
- Suleiman, W.; Joliveau, T.; Favier, E. A New Algorithm for 3D Isovists. In Advances in Spatial Data Handling; Richardson, D., Oosterom, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 157–173. [Google Scholar]
- Fisher-Gewirtzman, D. Can 3D Visibility Calculations along a Path Predict the Perceived Density of Participants Immersed in a Virtual Reality Environment. In Proceedings of the 11th Space Syntax Symposium, Lisbon, Portugal, 3–7 July 2017; Heitor, T., Serra, M., Silva, J.P., Bacharel, M., Silva, L.C.D., Eds.; Departamento de Engenharia Civil, Arquitetura e Georrecursos, Instituto Superior Técnico: Lisboa, Portugal, 2017. [Google Scholar]
- Bhatia, S.; Chalup, S.K.; Ostwald, M.J. Wayfinding: A method for the empirical evaluation of structural saliency using 3D Isovists. Archit. Sci. Rev. 2013, 56, 220–231. [Google Scholar] [CrossRef]
- Fisher-Gewirtzman, D.; Bruchim, E. Considering Variant Movement Velocities on the 3D Dynamic Visibility Analysis (DVA)—Simulating the perception of urban users: Pedestrians, cyclists and car drivers, Computing for a better tomorrow. In Proceedings of the 36th eCAADe Conference, 17–21 September 2018; Kepczynska-Walczak, A.B.S., Ed.; Lodz University of Technology: Lodz, Poland, 2018; pp. 569–576. [Google Scholar]
- Bielik, M.; Fuchkina, E.; Schneider, S.; Koenig, R. 2D and 3D Isovists for Visibility Analysis, DeCodingSpaces Toolbox for Grasshopper. 2019. Available online: https://toolbox.decodingspaces.net/tutorial-2d-and-3d-isovists-for-visibility-analysis/ (accessed on 10 April 2023).
- Oxman, R.; Gu, N. Theories and Models of Parametric Design Thinking. In Proceedings of the 33rd International Conference of ECAADE Conference, Vienna, Austria, 16–18 September 2015; pp. 2–6. [Google Scholar]
- Payne, A.; McNeel, B.; Davidson, S. The Grasshopper Primer, 3rd ed.; GitBook: Lyon, France, 2016. [Google Scholar]
- Issa, R. Essential Algorithms and Data Structures for Computational Design in Grasshopper, 1st ed.; Robert McNeel & Associates: Seattle, WA, USA, 2020. [Google Scholar]
- von Richthofen, A.; Knecht, K.; Miao, Y.; König, R. The ‘Urban Elements’ method for teaching parametric urban design to professionals. Front. Archit. Res. 2018, 7, 573–587. [Google Scholar] [CrossRef]
- Bielik, M.; Schneider, S.; König, R. Parametric Urban Patterns—Exploring and integrating graph-based spatial properties in parametric urban modelling. In Proceedings of the eCAADe 2012, Prague, Czech Republic, 12–14 September 2012. [Google Scholar]
- Gehl, J. Cities for People; ISLAND PRESS: Washington, DC, USA, 2010. [Google Scholar]
- Garnero, G.; Fabrizio, E. Visibility analysis in urban spaces: A raster-based approach and case studies. Environ. Plan. B Plan. Des. 2015, 42, 688–707. [Google Scholar] [CrossRef]
- Sayed, K.A.; Turner, A.; Hillier, B.; Iida, S.; Penn, A. Space Syntax Methodology; Bartlett School of Architecture, UCL: London, UK, 2014. [Google Scholar]
- Bao, W.; Gong, A.; Zhang, T.; Zhao, Y.; Li, B.; Chen, S. Mapping Population Distribution with High Spatiotemporal Resolution in Beijing Using Baidu Heat Map Data. Remote Sens. 2023, 15, 458. [Google Scholar] [CrossRef]
- Jacobs, A.; Appleyard, D. Toward an Urban Design Manifesto. J. Am. Plan. Assoc. 1987, 53, 112–120. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, Y.; Ma, L. A Quantitative Study on the Colour of City Landmark Landscape Architectures. J. Phys. Conf. Ser. 2019, 1288, 12011. [Google Scholar] [CrossRef]
- Balaban, C.Z.; Karimpur, H.; Röser, F.; Hamburger, K. Turn left where you felt unhappy: How affect influences landmark-based wayfinding. Cogn. Process. 2017, 18, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Bartie, P.; Mackaness, W.; Petrenz, P.; Dickinson, A. Identifying related landmark tags in urban scenes using spatial and semantic clustering. Comput. Environ. Urban Syst. 2015, 52, 48–57. [Google Scholar] [CrossRef]
- Palmiero, M.; Piccardi, L. The Role of Emotional Landmarks on Topographical Memory. Front. Psychol. 2017, 8, 763. [Google Scholar] [CrossRef] [PubMed]




















| Landmark | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | V11 | V12 | V13 | V14 | V15 | V16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1898.9 | 0 | 1587.1 | 1128.8 | 0 | 0 | 217.1 | 1438.5 | 479.3 | 0 | 0 | 4979.1 | 3477 | 3354.9 | 3963.4 | 2378.8 |
| B | 798.4 | 0 | 2273.7 | 3461.2 | 0 | 0 | 1752.8 | 4578.1 | 0 | 0 | 0 * | 4880.9 | 3229.4 | 3533.5 | 4370.1 | 2343.9 * |
| City Tissue | TP-District | XD-District |
|---|---|---|
| Block size | 435 hm2 | 204 hm2 |
| Population density | 275 persons/hm2 | 350 persons/hm2 |
| Building Groups Form | Building groups with a combination of high- and low-rise buildings | High-rise dominated building groups |
| Land Use | High degree of mixed functions, with residential land accounting for 28% of the total construction land | Low degree of mixed functions, with residential land use accounting for 52% of total construction land |
| Large-scale natural landscape landmarks | Yuelu Mountain, Tianma Mountain, Xiangjiang River, Orange Island | Xiangjiang River |
| Architectural and cultural landscape landmarks | A total of 14, located adjacent to or within the area, including 9 high-rise buildings. IFS-West Tower is the tallest building in Changsha, with a height of 452 m | A total of 27, with 11 high-rise buildings adjacent to or located in the area; at present, China CITIC Bank is the tallest building in the area, the height of 268 m. Nine super high-rise buildings are distant landmarks facing the area across the river |
| Construction situation | Mature built environment, all landmark buildings have been constructed | Mature built environment, but the A2-Beichen Landmark is a proposed project. There are 2 publicized schemes; the design height of scheme 1 is 268 m, and scheme 2 is 400 m |
| Type | TP-District | XD-District (Ha2 = 268 m) | XD-District (Ha2 = 400 m) |
|---|---|---|---|
| Riverside RD | 0.018 | 0.067 | 0.073 |
| NS-EW RD | 0.076 | - | - |
| EW RD | 0.098 | 0.160 | 0.158 |
| NS RD | 0.142 | 0.77 | 0.85 |
| ALL | 0.108 | 0.144 | 0.145 |
| Type | TP-District | XD-District (Ha2 = 268 m) | XD-District (Ha2 = 400 m) |
|---|---|---|---|
| Nearby high-rise building | 0.193 | 0.424 | 0.419 |
| Distant high-rise building | - | 0.260 | 0.243 |
| Cultural landscape | 0.160 | 0.313 | 0.333 |
| Natural landscape | 0.519 | - | - |
| ALL | 0.379 | 0.363 | 0.366 |
| Elements of Urban Imagery | Structural Landmark Salience |
|---|---|
| district | The visibility measure expressed in terms of decision nodes and landmarks is the morphological feature of the region. Differences in the morphology of the region lead to differences in the shading relation between the landscape resources of the regional landmarks and the surrounding environment. It is difficult to obtain good structural salience for landmarks with excessive occlusion of the environment. |
| edge | The structural salience of landmarks has broadened the scope of the analysis of urban areas. The edges of the visual field are formed by distant landmarks, and the edges of human activity are peripheral streets or large-scale natural landscape dividers within the area. |
| path | The wayfinding decision nodes are grouped according to the street alignment, and the decision nodes themselves express the sequential relationship of paths. 3D NL GAM incorporates landmark directional guidance interventions into the path selection analysis. |
| node | The NAIN values of the nodes at the decision point locations express the influence of landmark structural salience on the aggregation and accessibility of people, and the NACH values of the landmark node locations express the influence of landmark structural salience on the guidance of the wayfinding directions. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Hu, X.; Tang, J. Structural Landmark Salience Computation in Compact Urban Districts with 3D Node-Landmark Grid Analysis Model: A Case Study on Two Sample Districts in Changsha, China. Buildings 2023, 13, 1024. https://doi.org/10.3390/buildings13041024
Guo Y, Hu X, Tang J. Structural Landmark Salience Computation in Compact Urban Districts with 3D Node-Landmark Grid Analysis Model: A Case Study on Two Sample Districts in Changsha, China. Buildings. 2023; 13(4):1024. https://doi.org/10.3390/buildings13041024
Chicago/Turabian StyleGuo, Yang, Xijun Hu, and Jia Tang. 2023. "Structural Landmark Salience Computation in Compact Urban Districts with 3D Node-Landmark Grid Analysis Model: A Case Study on Two Sample Districts in Changsha, China" Buildings 13, no. 4: 1024. https://doi.org/10.3390/buildings13041024
APA StyleGuo, Y., Hu, X., & Tang, J. (2023). Structural Landmark Salience Computation in Compact Urban Districts with 3D Node-Landmark Grid Analysis Model: A Case Study on Two Sample Districts in Changsha, China. Buildings, 13(4), 1024. https://doi.org/10.3390/buildings13041024