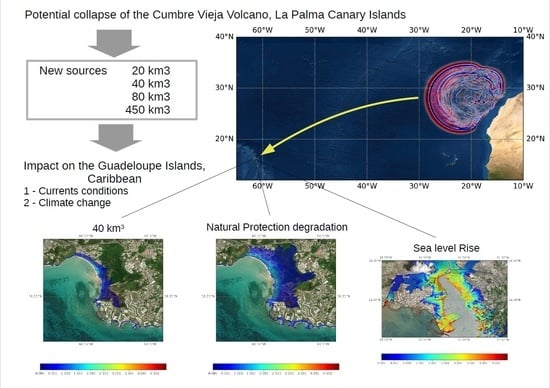
How Would the Potential Collapse of the Cumbre Vieja Volcano in La Palma Canary Islands Impact the Guadeloupe Islands? Insights into the Consequences of Climate Change
Abstract
:1. Introduction
The Collapse of the Cumbre Vieja Volcano and Tsunamis
2. Method
2.1. The Guadeloupe Archipelago
2.2. Model Implementation
2.3. Trans-Oceanic Model
2.4. Inundation Model
2.4.1. Grid
2.4.2. Bottom Friction
2.5. Climate Change Scenarios
3. Results
3.1. Time of Arrivals and Wave Heights
3.2. Wave Heights Distribution
3.3. Inundation
3.4. Climate Change-Related Tsunami Impact
3.4.1. Flooded Surfaces Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| C3AF | Consequences du Changement Climatique aux Antilles Françaises |
| SCHISM | Semi-implicit Cross-scale Hydroscience Integrated System Model |
| SLR | Sea level Rise |
References
- Kazama, M.; Noda, T. Damage statistics (Summary of the 2011 off the Pacific Coast of Tohoku Earthquake damage). Soils Found. 2012, 52, 780–792. [Google Scholar] [CrossRef] [Green Version]
- Pananont, P.; Srisomboon, R. 2004 tsunami in southern Thailand, lessons learned for the Thai communities. In Advances in Natural and Technological Hazards Research; Springer: Dordrecht, The Netherlands, 2014; pp. 399–416. [Google Scholar] [CrossRef]
- Zahibo, N.; Pelinovsky, E.N. Evaluation of tsunami risk in the Lesser Antilles. Nat. Hazards Earth Syst. Sci. 2001, 1, 221–231. [Google Scholar] [CrossRef]
- Pararas-Carayannis, G. Volcanic tsunami generating source mechanisms in the eastern Caribbean region. Sci. Tsunami Hazards 2004, 22, 74–114. [Google Scholar]
- Harbitz, C.B.; Glimsdal, S.; Bazin, S.; Zamora, N.; Løvholt, F.; Bungum, H.; Smebye, H.; Gauer, P.; Kjekstad, O. Tsunami hazard in the Caribbean: Regional exposure derived from credible worst case scenarios. Cont. Shelf Res. 2012, 38, 1–23. [Google Scholar] [CrossRef]
- Cordrie, L.; Gailler, A.; Escartin, J.; Feuillet, N.; Heinrich, P. Simulation of the 2004 tsunami of Les Saintes in Guadeloupe (Lesser Antilles) using new source constraints. Nat. Hazards 2020. [Google Scholar] [CrossRef]
- Zahibo, N.; Pelinovsky, E.N.; Yalciner, A.; Zaitsev, A.; Talipova, T.; Nikolkina, I.; Chernov, A.; Insel, I.; Dilmen, D.I.; Ozer, C. Trans-Atlantic Propagation of 1755 Tsunami and Its Effects on the French West Indies. Open Oceanogr. J. 2011, 5, 30–41. [Google Scholar] [CrossRef]
- Arnaud, G.; Krien, Y.; Abadie, S.; Dudon, B.; Zahibo, N. Transatlantic tsunami from Canary to the Caribbean. In XVèmes Journées, La Rochelle; Editions Paralia: La Rochelle, France, 2018; pp. 729–738. [Google Scholar] [CrossRef]
- Abadie, S.; Harris, J.C.; Grilli, S.T.; Fabre, R. Numerical modeling of tsunami waves generated by the flank collapse of the Cumbre Vieja Volcano (La Palma, Canary Islands): Tsunami source and near field effects. J. Geophys. Res. Ocean. 2012, 117, 1–26. [Google Scholar] [CrossRef]
- Ward, S.N.; Day, S. Cumbre Vieja Volcano-Potential collapse and tsunami at La Palma, Canary Islands. Geophys. Res. Lett. 2001, 28, 3397–3400. [Google Scholar] [CrossRef]
- Mader, C.L. Modeling the La Palma Landslaide Tsunami. Sci. Tsunami Hazard 2001, 19, 150–170. [Google Scholar]
- Løvholt, F.; Pedersen, G.; Gisler, G. Oceanic propagation of a potential tsunami from the La Palma Island. J. Geophys. Res. 2008, 113, C09026. [Google Scholar] [CrossRef] [Green Version]
- Harris, J.C.; Grilli, S.T.; Abadie, S.; Bakhsh, T.T. Near- and far-field tsunami hazard from the potential flank collapse of the Cumbre Vieja volcano. In Proceedings of the International Offshore and Polar Engineering Conference, Rhodes, Greece, 17–22 June 2012; pp. 242–249. [Google Scholar]
- Harris, J.C.; Grilli, S.T.; Abadie, S. Numerical Simulation of the Tsunami Generated by the Cumbre Vieja Flank Collapse (La Palma, Canary) by a Coupled Navier-Stokes/Boussinesq Approach. In Proceedings of the 13èmes Journées de l’Hydrodynamique, Chatou, France, 21–23 November 2012; pp. 1–13. [Google Scholar]
- Tehranirad, B.; Harris, J.C.; Grilli, A.R.; Grilli, S.T.; Abadie, S.; Kirby, J.T.; Shi, F. Far-Field Tsunami Impact in the North Atlantic Basin from Large Scale Flank Collapses of the Cumbre Vieja Volcano, La Palma. Pure Appl. Geophys. 2015, 172, 3589–3616. [Google Scholar] [CrossRef]
- Carracedo, J.C.; Day, S.J.; Guillou, H.; Gravestock, P. Later stages of volcanic evolution of La Palma, Canary Islands: Rift evolution, giant landslides, and the genesis of the Caldera de Taburiente. Geol. Soc. Am. Bull. 1999, 111, 755–768. [Google Scholar] [CrossRef]
- Pararas-Carayannis, G. Evaluation of the Threat of Mega Tsunami Generation from Postulated Massive Slope Failure of Island Stratovolcanoes on La Palma, Canary Island, and on The island of Hawaii. Sci. Tsunami Hazard 2002, 20, 251–277. [Google Scholar]
- Masson, D.G.; Harbitz, C.B.; Wynn, R.B.; Pedersen, G.; Løvholt, F. Submarine landslides: Processes, triggers and hazard prediction. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2006, 364, 2009–2039. [Google Scholar] [CrossRef] [PubMed]
- Gisler, G.; Weaver, R.; Gittings, M.L. SAGE Calculations of the Tsunami Threat from La Palma. Sci. Tsunami Hazards 2006, 24, 288–301. [Google Scholar]
- Abadie, S.; Paris, A.; Ata, R.; Le Roy, S.; Arnaud, G.; Poupardin, A.; Clous, L.; Heinrich, P.; Harris, J.; Pedreros, R.; et al. La Palma landslide tsunami: Calibrated wave source and assessment of impact on French territories. Nat. Hazards Earth Syst. Sci. 2020, 20, 3019–3038. [Google Scholar] [CrossRef]
- Comte, A. Evaluation Préliminaire des Risques d’Inondation, District de Guadeloupe; Technical Report; Direction de l’Environnement de l’Aménagement et du Logement: Basse Terre, Guadeloupe, 2012. [Google Scholar]
- Didenkulova, I.; Zahibo, N. Spectrum of the tide-gauge surface waves in Pointe-a-Pitre bay, Guadeloupe. In Geophysical Research Abstracts; SRef-ID: 1607-7962/gra/EGU2007-A-11258; Copernicus Publications: Göttingen, Germany, 2007; p. 11258. [Google Scholar]
- Woodworth, P.L. Seiches in the Eastern Caribbean. Pure Appl. Geophys. 2017, 174, 4283–4312. [Google Scholar] [CrossRef] [Green Version]
- Viroulet, S.; Sauret, A.; Kimmoun, O. Tsunami generated by a granular collapse down a rough inclined plane. arXiv 2014, arXiv:1402.6814v1. [Google Scholar] [CrossRef] [Green Version]
- Glimsdal, S.; Pedersen, G.K.; Harbitz, C.B.; Løvholt, F. Dispersion of tsunamis: Does it really matter? Nat. Hazards Earth Syst. Sci. 2013, 13, 1507–1526. [Google Scholar] [CrossRef] [Green Version]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation. Ocean. Model. 2012, 43–44, 36–51. [Google Scholar] [CrossRef]
- Wei, G.; Kirby, J.T.; Grilli, S.T.; Subramanya, R. A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J. Fluid Mech. 1995, 294, 71–92. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.T.; Tehranirad, B. Tsunami Benchmark Results For Spherical Coordinate Version of FUNWAVE-TVD; Technical Report; Center For Applied Coastal Research: Newark, Delaware, 2012. [Google Scholar]
- Grilli, A.R.; Grilli, S.T. Far-Field Tsunami Impact On The U.S. East Coast from an Extreme Flank Collapse of The Cumbre Vieja Volcano (Canary Islands); Technical Report; Research Report NO. CACR-13-03; Center for Applied Coastal Research: Newark, Delaware, 2013. [Google Scholar]
- Chen, Q. Fully Nonlinear Boussinesq-Type Equations for Waves and Currents over Porous Beds. J. Eng. Mech. 2006, 132, 220–230. [Google Scholar] [CrossRef]
- Kirby, J.T.; Shi, F.; Tehranirad, B.; Harris, J.C.; Grilli, S.T. Dispersive tsunami waves in the ocean: Model equations and sensitivity to dispersion and Coriolis effects. Ocean. Model. 2013, 62, 39–55. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless cross-scale modeling with SCHISM. Ocean. Model. 2016, 102, 64–81. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.J.; Baptista, A.M. SELFE: A Semi-Implicit Eulerian—Lagrangian Finite-Element Model For Cross-Scale Ocean Circulation. Ocean. Model. 2008, 21, 71–96. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Baptista, A.M. An Efficient and Robust Tsunami Model on Unstructured Grids. Part I: Inundation Benchmarks. Pure Appl. Geophys. 2008, 165, 2229–2248. [Google Scholar] [CrossRef]
- Janvier, F.; Kraszewski, M.; Levi-Valensin, M.; Trainel, S. (Eds.) Atlas Régional de L’occupation des Sols en France, Service de L’observation et des Statistiques (SOeS) ed.; Ministere de l’Environement de l’Energie et de la Mer, Commissariat général au Développement Durable (CGDD): Lyon, France, 2016; p. 168. [Google Scholar]
- Chow, V.T. Open-Channel Hydraulics; McGraw-Hill Civil Engineering Series; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Arcement, G.J.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; Technical Report; U.S. Geological Survey: Menlo Park, CA, USA, 1989. [Google Scholar] [CrossRef] [Green Version]
- Chauvaud, S.; Bouchon, C.; Manière, R. Cartographie des biocénoses marines de Guadeloupe à partir de données SPOT (récifs coralliens, phanérogames marines, mangroves). Oceanol. Acta 2001, 24, 3–16. [Google Scholar] [CrossRef] [Green Version]
- Oppenheimer, M.; Glavovic, B.; Hinkel, J.; de Wal, R.; Magnan, A.; Abd-Elgawad, A.; Cai, R.; Cifuentes-Jara, M.; DeConto, R.; Ghosh, T.; et al. Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; Pörtner, H.O., Roberts, D., Masson-Delmotte, V., Zhai, P., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Nicolai, M., Okem, A., et al., Eds.; Chapter 4; European Environment Agency: Copenhagen, Denmark, 2019; p. 169. [Google Scholar]
- Liu, W.C.; Hsu, M.H.; Wang, C.F. Modeling of Flow Resistance in Mangrove Swamp at Mouth of Tidal Keelung River, Taiwan. J. Waterw. Port Coastal Ocean. Eng. 2003, 129, 86–92. [Google Scholar] [CrossRef]
- Tehranirad, B.; Kirby, J.T. Does Morphological Adjustment during Tsunami Inundation Increase Levels of Hazard? Technical Report; University of Delaware: Newark, Delaware, 2016. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]












| CLCL 4 | Manning | Description |
|---|---|---|
| 1110 | 0.15 | Continuous urban fabric |
| 1120 | 0.12 | Discontinuous urban fabric |
| 1210 | 0.15 | Industrial or commercial units and public facilities |
| 1220 | 0.03 | Road and rail networks and associated land |
| 1230 | 0.05 | Port areas |
| 1240 | 0.02 | Airports |
| 1310 | 0.12 | Mineral extraction sites |
| 1320 | 0.12 | Dump sites |
| 1330 | 0.12 | Construction sites |
| 1410 | 0.04 | Green urban areas |
| 1420 | 0.04 | Sport and leisure facilities |
| 2111 | 0.06 | Nonirrigated arable land |
| 2112 | 0.18 | Sugar cane |
| 2120 | 0.04 | Permanently irrigated land |
| 2130 | 0.04 | Rice fields |
| 2210 | 0.04 | Vineyards |
| 2221 | 0.15 | Fruit trees and berry plantations |
| 2222 | 0.18 | Banana plantations |
| 2223 | 0.18 | Palm groves |
| 2224 | 0.18 | Coffee trees |
| 2230 | 0.09 | Olive groves |
| 2310 | 0.06 | Pastures, meadows and other permanent grasslands under agricultural use |
| 2410 | 0.06 | Annual crops associated with permanent crops |
| 2420 | 0.06 | Complex cultivation patterns |
| 2430 | 0.06 | Land principally occupied by agriculture, with significant areas of natural vegetation |
| 2440 | 0.12 | Agro-forestry areas |
| 3111 | 0.18 | Broad-leaved forest |
| 3112 | 0.2 | Mangrove forest |
| 3120 | 0.09 | Coniferous forest |
| 3130 | 0.18 | Mixed forest |
| 3210 | 0.04 | Natural grasslands |
| 3220 | 0.18 | Moors and heathland |
| 3230 | 0.1 | Sclerophyllous vegetation |
| 3240 | 0.15 | Transitional woodland-shrub |
| 3310 | 0.03 | Beaches, dunes, sands |
| 3320 | 0.03 | Bare rocks |
| 3330 | 0.04 | Sparsely vegetated areas |
| 3340 | 0.04 | Burnt areas |
| 3350 | 0.025 | Glaciers and perpetual snow |
| 4110 | 0.12 | Inland marshes |
| 4120 | 0.025 | Peat bogs |
| 4210 | 0.04 | Coastal salt marshes |
| 4220 | 0.03 | Salines |
| 4230 | 0.03 | Intertidal flats |
| 5111 | 0.025 | Water courses |
| 5112 | 0.025 | Temporary water course |
| 5120 | 0.025 | Water bodies |
| 5210 | 0.025 | Coastal lagoons |
| 5220 | 0.025 | Estuaries |
| 5230 | 0.025 | Sea and ocean |
| Manning | Description |
|---|---|
| 0.04 | Meadows |
| 0.09 | coral and other bentic habitats |
| 0.06 | coral and other bentic habitats—Meadows |
| 0.07 | coral and other bentic habitats—Seaweed |
| 0.04 | Meadows—Seaweed |
| 0.03 | Seaweed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arnaud, G.E.; Krien, Y.; Abadie, S.; Zahibo, N.; Dudon, B. How Would the Potential Collapse of the Cumbre Vieja Volcano in La Palma Canary Islands Impact the Guadeloupe Islands? Insights into the Consequences of Climate Change. Geosciences 2021, 11, 56. https://doi.org/10.3390/geosciences11020056
Arnaud GE, Krien Y, Abadie S, Zahibo N, Dudon B. How Would the Potential Collapse of the Cumbre Vieja Volcano in La Palma Canary Islands Impact the Guadeloupe Islands? Insights into the Consequences of Climate Change. Geosciences. 2021; 11(2):56. https://doi.org/10.3390/geosciences11020056
Chicago/Turabian StyleArnaud, Gael E., Yann Krien, Stéphane Abadie, Narcisse Zahibo, and Bernard Dudon. 2021. "How Would the Potential Collapse of the Cumbre Vieja Volcano in La Palma Canary Islands Impact the Guadeloupe Islands? Insights into the Consequences of Climate Change" Geosciences 11, no. 2: 56. https://doi.org/10.3390/geosciences11020056
APA StyleArnaud, G. E., Krien, Y., Abadie, S., Zahibo, N., & Dudon, B. (2021). How Would the Potential Collapse of the Cumbre Vieja Volcano in La Palma Canary Islands Impact the Guadeloupe Islands? Insights into the Consequences of Climate Change. Geosciences, 11(2), 56. https://doi.org/10.3390/geosciences11020056