Intrinsic Evaporative Cooling by Hygroscopic Earth Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Hygroscopic Properties of Geological Materials
2.2. Coupled Heat and Moisture Transport
2.3. Procedures Followed for Assigning Controlling Parameters
2.3.1. Textural Controls on Soil Properties
2.4. Simulation of Intrinsic Evaporative Cooling in Buildings
3. Results and Discussion
3.1. Soils
3.1.1. Soil Hygroscopic Properties
3.1.2. Intrinsic Evaporative Cooling by Mexican Green Roofs: Effect of Soil Texture
3.2. Adobe
3.2.1. Adobe Hygroscopic Properties
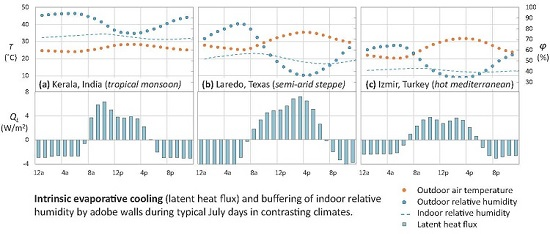
3.2.2. Intrinsic Evaporative Cooling by Adobe: Effects of Climate
3.3. Cob
3.3.1. Cob Hygroscopic Properties
3.3.2. Intrinsic Evaporative Cooling by Cob: Effect of Thickness
3.4. Unfired Earth Bricks
3.4.1. Earth Brick Hygroscopic Properties
3.4.2. Intrinsic Evaporative Cooling by Earth Bricks: Effect of Varying the Moisture Retention Curve
3.5. Rammed Earth
3.5.1. Rammed Earth Hygroscopic Properties
3.5.2. Intrinsic Evaporative Cooling by Rammed Earth: Effects of Liquid Transport Properties
3.6. Stone
3.6.1. Apulian Limestone Hygroscopic Properties
3.6.2. Intrinsic Evaporative Cooling by Apulian Limestone: Effect of Vapor Diffusion Resistance
4. Conclusions
4.1. Choose Materials with Broad Particle Size Distributions
4.2. Match Materials to the Climate of Interest
4.3. Orient Surfaces to Cool During Desired Hours
4.4. Dedicate Individual Elements to Either Evaporative or Conductive Cooling
4.5. Allow Indoor Buffering of Relative Humidity
4.6. Extend Theoretical and Experimental Efforts
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Davis, L.W.; Gertler, P.J. Contribution of air conditioning adoption to future energy use under global warming. Proc. Natl. Acad. Sci. USA 2015, 112, 5962–5967. [Google Scholar] [CrossRef] [PubMed]
- Isaac, M.; Van Vuuren, D.P. Modeling global residential sector energy demand for heating and air conditioning in the context of climate change. Energy Policy 2009, 37, 507–521. [Google Scholar] [CrossRef]
- Samuel, D.L.; Nagendra, S.S.; Maiya, M. Passive alternatives to mechanical air conditioning of building: A review. Build. Environ. 2013, 66, 54–64. [Google Scholar] [CrossRef]
- Santamouris, M.; Kolokotsa, D. Passive cooling dissipation techniques for buildings and other structures: The state of the art. Energy Build. 2013, 57, 74–94. [Google Scholar] [CrossRef]
- Reference Guide for Building Design and Construction v4; U.S. Green Building Council: Washington, DC, USA, 2013.
- Standard 55-2004, Thermal Environmental Conditions for Human Occupancy; ASHRAE American Society of Heating, Refrigerating, and Air-Conditioning Engineers: Atlanta, GA, USA, 2013.
- Weber, W.; Yannas, S. Lessons from Vernacular Architecture; Routledge: Abingdon-on-Thames, UK, 2013. [Google Scholar]
- Oliver, P. Encyclopedia of Vernacular Architecture of the World; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- May, J. Buildings Without Architects: A Global Guide to Everyday Architecture; Rizzoli: New York, NY, USA, 2010. [Google Scholar]
- Sadineni, S.B.; Madala, S.; Boehm, R.F. Passive building energy savings: A review of building envelope components. Renew. Sustain. Energy Rev. 2011, 15, 3617–3631. [Google Scholar] [CrossRef]
- Kang, D.; Strand, R.K. Modeling of simultaneous heat and mass transfer within passive down-draft evaporative cooling (PDEC) towers with spray in FLUENT. Energy Build. 2013, 62, 196–209. [Google Scholar] [CrossRef]
- Qiu, J.; Li, B.F.; Qiu, Y. Review of passive downdraught evaporative cooling technique and its application. Appl. Mech. Mater. 2013, 390, 691–695. [Google Scholar] [CrossRef]
- McDonald, R.I.; Weber, K.; Padowski, J.; Flörke, M.; Schneider, C.; Green, P.A.; Gleeson, T.; Eckman, S.; Lehner, B.; Balk, D.; et al. Water on an urban planet: Urbanization and the reach of urban water infrastructure. Glob. Environ. Chang. 2014, 27, 96–105. [Google Scholar] [CrossRef]
- Coutts, A.M.; Tapper, N.J.; Beringer, J.; Loughnan, M.; Demuzere, M. Watering our cities: The capacity for water sensitive urban design to support urban cooling and improve human thermal comfort in the Australian context. Prog. Phys. Geogr. 2012, 37, 2–28. [Google Scholar] [CrossRef]
- Kunzel, H.M. Simultaneous Heat and Moisture Transport in Building Components. Ph.D. Thesis, Fraunhofer Institute of Building Physics, Stuttgart, Germany, 1995. [Google Scholar]
- Künzel, H.M.; Kiessl, K. Calculation of heat and moisture transfer in exposed building components. Int. J. Heat Mass Transf. 1996, 40, 159–167. [Google Scholar] [CrossRef]
- Barry, R.G.; Chorley, R.J. Atmosphere, Weather and Climate; Routledge: Abingdon-on-Thames, UK, 2009. [Google Scholar]
- Or, D.; Lehmann, P.; Shahraeeni, E.; Shokri, N. Advances in soil evaporation physics—A review. Vadose Zone J. 2013, 12, 2011–2022. [Google Scholar] [CrossRef]
- Rael, R. Earth Architecture; Princeton Architectural Press: New York, NY, USA, 2009. [Google Scholar]
- Oliver, P. Dwellings: The Vernacular House World Wide; Phaidon: London, UK, 2003. [Google Scholar]
- Cardinale, N.; Rospi, G.; Stefanizzi, P.; Augenti, V. Thermal properties of the vernacular buildings envelopes: The case of the “Sassi di Matera” and Trulli di Alberobello. Int. J. Energy Environ. 2011, 2, 605–614. [Google Scholar]
- Priya, R.S.; Sundarraja, M.; Radhakrishnan, S.; Vijayalakshmi, L. Solar passive techniques in the vernacular buildings of coastal regions in Nagapattinam, TamilNadu-India–A qualitative and quantitative analysis. Energy Build. 2012, 49, 50–61. [Google Scholar] [CrossRef]
- Gagliano, A.; Patania, F.; Nocera, F.; Signorello, C. Assessment of the dynamic thermal performance of massive buildings. Energy Build 2014, 72, 361–370. [Google Scholar] [CrossRef]
- Algifri, A.; Gadhi, S.B.; Nijaguna, B. Thermal behaviour of adobe and concrete houses in Yemen. Renew. Energy 1992, 2, 597–602. [Google Scholar] [CrossRef]
- Rempel, A.R.; Rempel, A.W. Rocks, clays, water, and salts: Highly durable, infinitely rechargeable, eminently controllable thermal batteries for buildings. Geosciences 2013, 3, 63–101. [Google Scholar] [CrossRef]
- Tan, L.B. Study on sustainable use of raw soil material in rural houses design in Western China. Adv. Mater. Res. 2012, 476, 1714–1717. [Google Scholar] [CrossRef]
- Duffin, R.; Knowles, G. Temperature control of buildings by adobe wall design. Sol. Energy 1981, 27, 241–249. [Google Scholar] [CrossRef]
- Bahadori, M.N.; Haghighat, F. Weekly storage of coolness in heavy brick and adobe walls. Energy Build. 1985, 8, 259–270. [Google Scholar] [CrossRef]
- Zhai, Z.J.; Previtali, J.M. Ancient vernacular architecture: Characteristics categorization and energy performance evaluation. Energy Build. 2010, 42, 357–365. [Google Scholar] [CrossRef]
- Singh, M.K.; Mahapatra, S.; Atreya, S. Solar passive features in vernacular architecture of North-East India. Sol. Energy 2011, 85, 2011–2022. [Google Scholar] [CrossRef]
- Morony, J.J. Adobe and latent heat: A critical connection. In Proceedings of the Second Annual Conference of the Adobe Association of the Southwest, El Rito, NM, USA, 18–21 May 2005.
- Morony, J.J. Adobe as phase-change material (PCM): Concerning a proper classification for an earthen building material. In Proceedings of the Fourth Annual Conference of the Adobe Association of the Southwest, El Rito, NM, USA, 18–20 May 2007.
- Pandit, R.; Schick, M.; Wortis, M. Systematics of multilayer adsorption phenomena on attractive substrates. Phys. Rev. B 1982, 26, 5112–5140. [Google Scholar] [CrossRef]
- Van Oss, C.; Giese, R. The hydrophilicity and hydrophobicity of clay minerals. Clays Clay Miner. 1995, 43, 474–477. [Google Scholar] [CrossRef]
- Lu, N.; Khorshidi, M. Mechanisms for soil-water retention and hysteresis at high suction range. J. Geotech. Geoenviron. Eng. 2015, 141, 04015032. [Google Scholar] [CrossRef]
- Resurreccion, A.C.; Moldrup, P.; Tuller, M.; Ferre, T.; Kawamoto, K.; Komatsu, T.; De Jonge, L.W. Relationship between specific surface area and the dry end of the water retention curve for soils with varying clay and organic carbon contents. Water Resour. Res. 2011, 47, W06522. [Google Scholar] [CrossRef]
- Schneider, M.; Goss, K.U. Prediction of the water sorption isotherm in air dry soils. Geoderma 2012, 170, 64–69. [Google Scholar] [CrossRef]
- Tuller, M.; Or, D. Water films and scaling of soil characteristic curves at low water contents. Water Resour. Res. 2005, 41, W09403. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Tuller, M.; Or, D.; Dudley, L.M. Adsorption and capillary condensation in porous media: Liquid retention and interfacial configurations in angular pores. Water Resour. Res. 1999, 35, 1949–1964. [Google Scholar] [CrossRef]
- Buck, A.L. New equations for computing vapor pressure and enhancement factor. J. Appl. Meteorol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Kehrer, M.; Pallin, S.; Harmon, A.; Goldberg, L.F. Hygrothermal Simulation of Foundations: Part 1 Soil Material Properties; Technical Report; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA, 2012. [Google Scholar]
- Becker, B.; Fricke, B. Effects of saturation and dry density on soil thermal conductivity. In Proceedings of the 3rd International Conference on Heat Pumps in Cold Climates, Wolfville, NS, Canada, 11–12 August 1997; pp. 121–136.
- Saxton, K.; Rawls, W.; Romberger, J.; Papendick, R. Estimating generalized soil-water characteristics from texture. Soil Sci. Soc. Am. J. 1986, 50, 1031–1036. [Google Scholar] [CrossRef]
- Moldrup, P.; Olesen, T.; Gamst, J.; Schjønning, P.; Yamaguchi, T.; Rolston, D. Predicting the gas diffusion coefficient in repacked soil water-induced linear reduction model. Soil Sci. Soc. Am. J. 2000, 64, 1588–1594. [Google Scholar] [CrossRef]
- Yan, Z.; Lam, J.C.; Liu, J. Experimental studies on the thermal and moisture properties of rammed earth used in adobe buildings in China. Archit. Sci. Rev. 2005, 48, 55–60. [Google Scholar] [CrossRef]
- Collet, F.; Serres, L.; Miriel, J.; Bart, M. Study of thermal behaviour of clay wall facing south. Build. Environ. 2006, 41, 307–315. [Google Scholar] [CrossRef]
- Collet, F.; Bart, M.; Serres, L.; Miriel, J. Porous structure and hydric properties of cob. J. Porous Media 2010, 13, 111–124. [Google Scholar] [CrossRef]
- Cagnon, H.; Aubert, J.; Coutand, M.; Magniont, C. Hygrothermal properties of earth bricks. Energy Build. 2014, 80, 208–217. [Google Scholar] [CrossRef]
- Allinson, D.; Hall, M. Hygrothermal analysis of a stabilised rammed earth test building in the UK. Energy Build. 2010, 42, 845–852. [Google Scholar] [CrossRef]
- Hall, M.; Allinson, D. Assessing the effects of soil grading on the moisture content-dependent thermal conductivity of stabilised rammed earth materials. Appl. Therm. Eng. 2009, 29, 740–747. [Google Scholar] [CrossRef]
- Hall, M.; Allinson, D. Analysis of the hygrothermal functional properties of stabilised rammed earth materials. Build. Environ. 2009, 44, 1935–1942. [Google Scholar] [CrossRef] [Green Version]
- Andriani, G.F.; Walsh, N. Petrophysical and mechanical properties of soft and porous building rocks used in Apulian monuments (south Italy). Geol. Soc. Lond. Spec. Publ. 2010, 333, 129–141. [Google Scholar] [CrossRef]
- Andriani, G.; Walsh, N. Fabric, porosity and water permeability of calcarenites from Apulia (SE Italy) used as building and ornamental stone. Bull. Eng. Geol. Environ. 2003, 62, 77–84. [Google Scholar]
- Beck, K.; Al-Mukhtar, M.; Rozenbaum, O.; Rautureau, M. Characterization, water transfer properties and deterioration in tuffeau: Building material in the Loire Valley–France. Build. Environ. 2003, 38, 1151–1162. [Google Scholar] [CrossRef]
- Reynolds, C.; Jackson, T.; Rawls, W. Estimating soil water-holding capacities by linking the Food and Agriculture Organization soil map of the world with global pedon databases and continuous pedotransfer functions. Water Resour. Res. 2000, 36, 3653–3662. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; Van Genuchten, M.T. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Jensen, D.K.; Tuller, M.; de Jonge, L.W.; Arthur, E.; Moldrup, P. A new two-stage approach to predicting the soil water characteristic from saturation to oven-dryness. J. Hydrol. 2015, 521, 498–507. [Google Scholar] [CrossRef]
- Lu, N. Generalized soil water retention equation for adsorption and capillarity. J. Geotech. Geoenviron. Eng. 2016, 04016051. [Google Scholar] [CrossRef]
- Peters, A. Simple consistent models for water retention and hydraulic conductivity in the complete moisture range. Water Resour. Res. 2013, 49, 6765–6780. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Hydraulic properties of porous media and their relation to drainage design. Trans. ASAE 1964, 7, 26–0028. [Google Scholar]
- Rawls, W.; Brakensiek, D.; Saxtonn, K. Estimation of soil water properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- U.S. Department of Energy. EnergyPlus 8.4. 2015. Available online: http://energyplus.net (accessed on 27 August 2016). [Google Scholar]
- EnergyPlus Engineering Reference; U.S. Department of Energy: Washington, DC, USA, 2015.
- U.S. Department of Energy. Auxiliary Programs for EnergyPlus. 2015. Available online: http://energyplus.net (accessed on 27 August 2016). [Google Scholar]
- Legacy OpenStudio 1.0.14; National Renewable Energy Laboratory, U.S. Department of Energy: Golden, CO, USA, 2015.
- Morony, J.J. The Mexican green roof. In Proceedings of the Fifth International Conference on Earth Architecture, El Rito, NM, USA, 15 May 2009.
- Minke, G. Building with Earth: Design and Technology of a Sustainable Architecture, 3rd ed.; Walter de Gruyter: Berlin, Germany, 2012. [Google Scholar]
- Austin, G.S. Adobe as a building material. N. M. Geol. 1984, 69–71. [Google Scholar]
- Van Beek, G.W.; Van Beek, O. Glorious Mud!: Ancient and Contemporary Earthen Design and Construction in North Africa, Western Europe, the Near East, and Southwest Asia; Smithsonian Institution: Washington, DC, USA, 2013. [Google Scholar]
- McHenry, P.G. Adobe and Rammed Earth Buildings: Design and Construction; University of Arizona Press: Tucson, AZ, USA, 1984. [Google Scholar]
- Lertwattanaruk, P.; Choksiriwanna, J. The physical and thermal properties of adobe brick containing bagasse for earth construction. J. Archit. Plan. Res. Stud. 2011, 5, 187–199. [Google Scholar]
- Hadjri, K.; Osmani, M.; Baiche, B.; Chifunda, C. Attitudes towards earth building for Zambian housing provision. In Proceedings of the Institution of Civil Engineers: Engineering Sustainability; Thomas Telford Publishing: London, UK, 2007; Volume 160, pp. 141–149. [Google Scholar]
- Pacheco-Torgal, F.; Jalali, S. Earth construction: Lessons from the past for future eco-efficient construction. Constr. Build. Mater. 2012, 29, 512–519. [Google Scholar] [CrossRef] [Green Version]
- Revuelta-Acosta, J.; Garcia-Diaz, A.; Soto-Zarazua, G.; Rico-Garcia, E. Adobe as a sustainable material: A thermal performance. J. Appl. Sci. 2010, 10, 2211–2216. [Google Scholar]
- Yan, Z.; Liu, J.; Wang, R. Experimental study of moisture absorption isotherms of adobe building materials. J. Xian Univ. Archit. Technol. 2003, 35, 327–353. [Google Scholar]
- McCann, J. Clay and Cob Buildings; Shire Publications: London, UK, 2004. [Google Scholar]
- Miccoli, L.; Müller, U.; Fontana, P. Mechanical behaviour of earthen materials: A comparison between earth block masonry, rammed earth and cob. Constr. Build. Mater. 2014, 61, 327–339. [Google Scholar] [CrossRef]
- Hamard, E.; Cazacliu, B.; Razakamanantsoa, A.; Morel, J.C. Cob, a vernacular earth construction process in the context of modern sustainable building. Build. Environ. 2016, 106, 103–119. [Google Scholar] [CrossRef]
- Goodhew, S.; Griffiths, R. Sustainable earth walls to meet the building regulations. Energy Build. 2005, 37, 451–459. [Google Scholar] [CrossRef]
- Lawrence, M.; Heath, A.; Walker, P. Mortars for thin unfired clay masonry walls. In Proceedings of the LEHM 5th International Conference on Building with Earth, Koblenz, Germany, 9–12 October 2008; pp. 66–73.
- Rempel, A.R.; Rempel, A.W.; Gates, K.R.; Shaw, B. Climate-responsive thermal mass design for Pacific Northwest sunspaces. Renew. Energy 2016, 85, 981–993. [Google Scholar] [CrossRef]
- McGregor, F.; Heath, A.; Shea, A.; Lawrence, M. The moisture buffering capacity of unfired clay masonry. Build. Environ. 2014, 82, 599–607. [Google Scholar] [CrossRef] [Green Version]
- Maillard, P.; Aubert, J. Effects of the anisotropy of extruded earth bricks on their hygrothermal properties. Constr. Build. Mater. 2014, 63, 56–61. [Google Scholar] [CrossRef]
- Morton, T. Feat of clay. Mater. World 2006, 14, 23–24. [Google Scholar]
- El Fgaier, F.; Lafhaj, Z.; Brachelet, F.; Antczak, E.; Chapiseau, C. Thermal performance of unfired clay bricks used in construction in the north of France: Case study. Case Stud. Constr. Mater. 2015, 3, 102–111. [Google Scholar] [CrossRef]
- Soebarto, V. Analysis of indoor performance of houses using rammed earth walls. In Proceedings of the 11th International IBPSA Conference, Glasgow, Scotland, 27–30 July 2009; pp. 1530–1537.
- Rincón, L.; Serrano, S.; Cabeza, L.; González, B.; Navarro, A.; Bosch, M. Experimental rammed earth prototypes in Mediterranean climate. In Proceedings of the International Conference on Vernacular Heritage, Sustainability and Earthen Architecture—Earthen Architecture: Past, Present and Future, Valencia, Spain, 11–13 September 2014; pp. 311–316.
- Hall, M.; Djerbib, Y. Moisture ingress in rammed earth: Part 1—The effect of soil particle-size distribution on the rate of capillary suction. Constr. Build. Mater. 2004, 18, 269–280. [Google Scholar] [CrossRef]
- Hall, M.; Djerbib, Y. Moisture ingress in rammed earth: Part 2—The effect of soil particle-size distribution on the absorption of static pressure-driven water. Constr. Build. Mater. 2006, 20, 374–383. [Google Scholar] [CrossRef]
- Hall, M.; Allinson, D. Transient numerical and physical modelling of temperature profile evolution in stabilised rammed earth walls. Appl. Therm. Eng. 2010, 30, 433–441. [Google Scholar] [CrossRef]
- Bark, L.G. Bee-hive dwellings of Apulia. Antiquity 1932, 6, 407–410. [Google Scholar] [CrossRef]
- Ruggiero, G.; Dal Sasso, S.; Loisi, R.V.; Verdiani, G. Characteristics and distribution of trulli constructions in the area of the site of community importance Murgia of Trulli. J. Agric. Eng. 2013, 44, 13. [Google Scholar] [CrossRef]
- Dipasquale, L.; Silva, N.J. Corbelled domes of Apulia (Italy). In Earthen Domes and Habitats; Mecca, S., Dipasquale, L., Eds.; Editorial ETS: Pisa, Italy, 2009; pp. 123–142. [Google Scholar]
- Cardinale, N.; Rospi, G.; Stefanizzi, P. Energy and microclimatic performance of Mediterranean vernacular buildings: The Sassi district of Matera and the Trulli district of Alberobello. Buil. Environ. 2013, 59, 590–598. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Barreneche, C.; Miró, L.; Morera, J.M.; Bartolí, E.; Fernández, A.I. Low carbon and low embodied energy materials in buildings: A review. Renew. Sustain. Energy Rev. 2013, 23, 536–542. [Google Scholar] [CrossRef]
- Reddy, B.V.; Jagadish, K. Embodied energy of common and alternative building materials and technologies. Energy Build. 2003, 35, 129–137. [Google Scholar] [CrossRef]
- Franzen, C.; Mirwald, P. Moisture content of natural stone: Static and dynamic equilibrium with atmospheric humidity. Environ. Geol. 2004, 46, 391–401. [Google Scholar] [CrossRef]
- Krus, M. Moisture Transport and Storage Coefficients of Porous Mineral Building Baterials: Theoretical Principles and New Test Methods; Fraunhofer IRB Verlag: Stuttgart, Germany, 1996. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]


















| Symbol | (Units) | Definition | Comment |
|---|---|---|---|
| C | (J/(kg·K)) | dry specific heat capacity | typical range: 700–2500 J/(kg·K) |
| (J/(kg·K)) | liquid specific heat capacity | 4200 J/(kg·K) | |
| D | (m2/s) | liquid transport coefficient | |
| g | (m/s2) | acceleration of gravity | 9.8 m/s2 |
| i | index for spatial discretization | 12 nodes span each building element | |
| j | index for temporal discretization | typically reported in hourly increments | |
| k | (W/(m·K)) | thermal conductivity | function of moisture content |
| K | (m/s) | hydraulic conductivity | approximated for soils using Equation (9) |
| L | (J/kg) | latent heat of vaporization | 2.265 × 106 J/kg |
| M | (kg/kg) | average water mass ratio | averaged across building element |
| n | porosity | pore volume divided by total volume | |
| (Pa) | ambient air pressure | taken as 101.3 kPa | |
| (Pa) | vapor pressure | ||
| (Pa) | saturation vapor pressure | function of temperature; see Figure 1 | |
| (W/m2) | conductive heat flux | evaluated between nodes with Equation (10) | |
| (W/m2) | latent heat flux | evaluated between nodes with Equation (11) | |
| (W/m2) | total latent heat flux | evaluated across timesteps with Equation (12) | |
| R | (J/(mol·K)) | gas constant | 8.314 J/(mol·K) |
| S | (kg/m3) | moisture storage capacity | |
| t | (s) | time | |
| T | (K) | temperature | given in °C where noted |
| (m3/mol) | partial molar volume of water | 18 × 10−6 m3/mol | |
| W | (kg/m3) | moisture content | function of relative humidity |
| x | (m) | distance | measured relative to exterior surface |
| X | (m) | building element thickness | either wall or roof |
| δ | (kg/(m·s·Pa)) | vapor diffusion coefficient in air | related to T through Equation (5) |
| (s) | conduction time scale | ; see Section 3.6.2 | |
| (s) | vapor diffusion time scale | ; see Section 3.6.2 | |
| (m) | incremental distance | used in scaling arguments for and | |
| Γ | liquid–vapor transport ratio | defined by Equation (3) | |
| μ | vapor diffusion resistance factor | function of relative humidity | |
| φ | relative humidity | ||
| (kg/m3) | dry density | times density of matrix material | |
| (kg/m3) | liquid density | 1000 kg/m3 | |
| Ψ | (Pa) | water potential | related to φ through Equation (1) |
| Material | Parameter | Value | Source/Comments |
|---|---|---|---|
| C | 850 J/(kg·K) | [43] | |
| 1270–1580 kg/m3 | ([43], Table 2) | ||
| n | 40%–52% | ([43], Table 2) | |
| Soils | k | see Figure 3d | [43,44] |
| W | see Figure 3a | Equation (6) [45] | |
| μ | see Figure 3b | Equation (8) [46] | |
| D | see Figure 3c | Equation (9) [45] | |
| C, | 900 J/(kg·K), 1800 kg/m3 | [47] | |
| n | 32% | [47] | |
| Adobe | k | dry 0.683 W/(m·K) | ([47], Table 3) |
| W | see Figure 7a | ([47], Figure 6) | |
| μ | see Figure 7b | Equation (8) | |
| D | sandy loam, Equation (9) | , vapor transport dominates | |
| C, | 815 J/(kg·K), 1550 kg/m3 | [48] | |
| n | 42% | [49] | |
| Cob | k | dry 0.4 W/(m·K) [49] | loam [43,44] |
| W | see Figure 7a | ([49], Figure 6) | |
| μ | see Figure 7b | Equation (8) | |
| D | loam, Equation (9) | , vapor transport dominates | |
| C, | 990 J/(kg·K), 2060 kg/m3 | [50] | |
| n | 22% | estimate from | |
| Unfired | k | dry 0.6 W/(m·K) | ([50], Figure 10) |
| earth brick | W | see Figure 7a) | “Brick 1” ([50], Figure 6) |
| μ | see Figure 7b | Equation (8) | |
| D | clay loam, Equation (9) | , vapor transport dominates | |
| C, | 868 J/(kg·K), 1900 kg/m3 | [51] | |
| n | 29.5% | [51] | |
| Rammed | k | dry 0.643 W/(m·K) [51] | linear to 1.158 W/(m·K) [52] |
| earth | W | see Figure 14a | ([51], Figure 4) |
| μ | see Figure 14b | Equation (8) to [51] | |
| D | see Figure 15 | “Maximum” from [53] | |
| C | 1200, 1200, 900 J/(kg·K) | ([54], Table 3) | |
| 1440, 1392, 1540 kg/m3 | ([54], Table 2) | ||
| Limestone | n | 48%, 49%, 44% | [54,55] |
| (fine, medium, coarse) | k | dry 0.9, 0.8, 0.7 W/(m·K) | ([54], Table 3) |
| W | see Figure 14a | modified from ([56], Figure 7) | |
| μ | see Figure 17 | “Original” Equation (8); see Figure 14b | |
| D | from Equation (13) | , vapor transport dominates |
| Material | Location | Köppen Climate | Description | Weather File |
|---|---|---|---|---|
| Soils, adobe | Laredo, TX, USA | BSh | Hot semi-arid grassland | USA_TX_Laredo.Intl. AP.722520_TMY3 |
| Adobe | Kerala, India | Aw/Am | Tropical monsoon/savanna | IND_Trivandrum. 433710_IWEC |
| Adobe | Yuma, AZ, USA | BWh | Hot desert | USA_AZ_Yuma.Intl. AP.722800_TMY3 |
| Adobe | Izmir, Turkey | Csa | Dry-summer Mediterranean | TUR_Izmir. 172180 _IWEC |
| Adobe | Xi’an, Shaanxi, China | Cwa | Humid-summer subtropical | CHN_Shaanxi.Xian. 570360 _CSWD |
| Adobe | Kunming, Yunnan, China | Cwb | Cooler humid subtropical | CHN_Yunnan.Kun- ming. 567780_IWEC |
| Cob | Nantes, France | Cfb | Marine west coast | FRA_Nantes. 072220 _IWEC |
| Extruded brick | Clermont-Ferrand, France | Cfb | Marine west coast | FRA_Clermont-Fer- rand. 074600_IWEC |
| Rammed earth | Birmingham, UK | Cfb | Marine west coast | GBR_Birmingham. 035340_IWEC |
| Limestone | Gioia del Colle, Italy | Cfa | Fully humid subtropical | ITA_Gioia.del.Colle. 163120_IGDG |
| Location | Latitude | Global Horizontal Radiation (Wh/m2 Day) | Direct Normal Radiation (Wh/m2 Day) | Cloud Cover (%) | Evaporative Heat Flux (Wh/m2 Day) |
|---|---|---|---|---|---|
| Kerala, India | 10.8° N | 215 | 125 | 76 | 44.2 |
| Laredo, TX, USA | 27.5° N | 280 | 255 | 38 | 55.6 |
| Yuma, AZ, USA | 32.7° N | 295 | 310 | 50 | 32.5 |
| Izmir, Turkey | 38.4° N | 310 | 290 | 8 | 30.5 |
| Xi’an, Shaanxi, China | 34.3° N | 190 | 95 | 45 | 30.8 |
| Kunming, Yunnan, China | 24.9° N | 150 | 25 | 82 | 26.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rempel, A.R.; Rempel, A.W. Intrinsic Evaporative Cooling by Hygroscopic Earth Materials. Geosciences 2016, 6, 38. https://doi.org/10.3390/geosciences6030038
Rempel AR, Rempel AW. Intrinsic Evaporative Cooling by Hygroscopic Earth Materials. Geosciences. 2016; 6(3):38. https://doi.org/10.3390/geosciences6030038
Chicago/Turabian StyleRempel, Alexandra R., and Alan W. Rempel. 2016. "Intrinsic Evaporative Cooling by Hygroscopic Earth Materials" Geosciences 6, no. 3: 38. https://doi.org/10.3390/geosciences6030038
APA StyleRempel, A. R., & Rempel, A. W. (2016). Intrinsic Evaporative Cooling by Hygroscopic Earth Materials. Geosciences, 6(3), 38. https://doi.org/10.3390/geosciences6030038