Continuously Wavelength-Tunable First-Order Narrowband Fiber Comb Filter Using Composite Combination of Wave Retarders

Abstract

Here, by harnessing a composite combination of wave retarders, we propose and experimentally demonstrate a first-order narrowband fiber comb filter capable of continuously tuning its wavelength, of which the filter structure is on the fundamental basis of a polarization–diversity loop structure. The demonstrated comb filter consists of a polarizing beam splitter (PBS), two high birefringence fiber (HBF) segments of the same length, an ordered wave retarder combination (WRC) of a quarter-wave retarder (QWR) and a half-wave retarder (HWR) before the first HBF segment, and an ordered WRC of an HWR and a QWR before the second HBF segment. The second HBF segment is butt-coupled to one port of the PBS so that its principal axis should be 22.5° away from the horizontal axis of the PBS. Taking the filter transmittance obtained by Jones calculus into consideration, we found the azimuth orientation angle (AOA) sets of the four wave retarders, which could allow extra phase shifts (ψ’s) ranging from 0° to 360° to be induced in the narrowband transmittance function. From filter transmission spectra calculated according to the AOA sets found above, it is confirmed that the first-order narrowband comb spectrum can be continuously tuned by properly controlling the AOA’s, clearly indicating the continuous wavelength tunability based on a composite combination of ordered wave retarders. This theoretical prediction was verified by actually constructing the proposed filter. Then, it is concluded that our filter employing the composite combination of wave retarders can be continuously frequency-tuned by properly controlling the AOA’s of the wave retarders.

1. Introduction

Up to the present, much attention has been given to fiber comb filters, which manipulate optical signals routed in optical systems, due to their structural simplicity, good fiber compatibility, and great facility to fabricate. They have been utilized for the implementation of optical pulse train generation [1], multiwavelength switching or lasing [2,3,4,5], optical label switching [6,7], and microwave signal processing [8,9,10]. Flexible adjustment of the wavelength (or frequency) location of the transmission bands of a comb filter is a crucial function to pass or reject the desired wavelength component in wavelength-division-multiplexing-based optical communication systems. While continuous wavelength tunability has been realized in numerous comb filters based on a Sagnac birefringence loop [11,12], a Lyot-type birefringence interferometer [13,14], and a Mach–Zehnder interferometer (MZI) [15,16], a comb filter incorporating a polarization–diversity loop structure (PDLS) [17,18,19,20] offers the most effective and diverse wavelength controllability (including wavelength switching and tuning) in comparison with conventional comb filters. PDLS-based comb filters are also more robust to external physical perturbations, such as ambient temperature and pressure changes, than MZI-based comb filters [15,16]. Over the last three years, several studies have been conducted for realization of continuous wavelength tunability in periodic comb spectra of PDLS-based fiber comb filters [21,22,23,24]. A continuously wavelength-tunable PDLS-based zeroth-order comb filter employing one birefringent component, i.e., a high-birefringence fiber (HBF) segment, was proposed by using three ordered wave retarder combinations (WRC’s): Two quarter-wave retarders (QWR’s), an ordered WRC of a QWR and a half-wave retarder (HWR), and another ordered WRC of an HWR and a QWR [21]. In addition to the zeroth-order comb filters, there have been series of reports on the continuous control of the wavelength location of passband-flattened and -narrowed transmission spectra, which could be obtained in a PDLS-based first-order comb filter with two HBF segments [22,23,24]. In terms of these first-order wavelength-tunable comb filters, an ordered WRC of an HWR and a QWR was positioned before each of two HBF segments. By controlling the azimuth orientation angles (AOA’s) of the wave retarders comprising the above comb filters, an incremental phase delay (ψ) of 0°–360° can be introduced into the transmittance function of each filter. In these previous works on the first-order comb filters [22,23,24], only the ordered WRC of an HWR and a QWR was employed and placed before each HBF segment for implementation of the continuous modulation of the extra phase delay ψ in the filter transmittance function. Another ordered WRC of a QWR and an HWR may also be a candidate to achieve the continuous ψ modulation. To the best of our knowledge, the continuous wavelength tuning of passband-narrowed transmission spectra was not accomplished by using an ordered WRC of a QWR and an HWR in the PDLS-based first-order comb filter. The introduction of the new ordered WRC will lead to completely different AOA sets of the wave retarders, required for the continuous frequency tuning of the filter spectrum. In particular, recent previous works failed to implement the continuous wavelength tuning of passband-narrowed transmission spectra [22] or utilized an additional HWR to increase the visibility of passband-narrowed transmission spectra leading to the use of five wave retarders for the desired wavelength-tuning operation [23,24]. Here, we theoretically and experimentally demonstrate a narrowband fiber comb filter capable of continuously tuning its wavelength position with a composite combination of wave retarders in the PDLS. The demonstrated PDLS-based filter consists of a polarizing beam splitter (PBS), two HBF segments of equal length, an ordered WRC of a QWR and an HWR before the first HBF segment, and an ordered WRC of an HWR and a QWR ahead of the second HBF segment. The second HBF segment is butt-coupled to one port of the PBS so that its slow axis should be oriented at 22.5° with respect to the horizontal axis of the PBS, which enables the maximum spectral visibility without the use of an additional HWR. As described in Section 2, considering the filter transmittance obtained by Jones calculus, we found the AOA sets of the four wave retarders, which could bring extra phase shifts (ψ’s) from 0° to 360° to the narrowband transmittance function. From filter transmission spectra calculated according to the AOA sets found above, it is confirmed that the narrowband comb spectrum can be continuously frequency-tuned by properly adjusting the AOA’s, clearly demonstrating the continuous wavelength tunability of the proposed comb filter adopting composite WRC’s. As can be found in Section 3, this theoretical prediction is verified by experimental demonstration showing eight measured narrowband transmission spectra spaced 0.1 nm apart in wavelength. Finally, a brief summary and conclusion on our continuously wavelength-tunable narrowband comb filter are given in Section 4.

2. Principle of Operation

Figure 1a shows a schematic diagram of the proposed filter composed of a PBS, two HBF segments of the same length, an ordered WRC of a QWR and an HWR (designated as QWR 1 and HWR 1, respectively) before the first HBF segment depicted as HBF 1, and an ordered WRC of an HWR and a QWR (designated as HWR 2 and QWR 2, respectively) in front of the second HBF segment depicted as HBF 2. HBF 2 is butt-coupled to port 3 of the PBS so that its slow axis should be oriented at 22.5° with respect to the horizontal axis of the PBS. This butt-coupling between HBF 2 and the PBS maximizes the extinction ratio of the narrowband comb spectrum of the filter. Each ordered WRC can modify the effective phase delay difference between the fast and slow axes of HBF 1 or HBF 2. A change in this effective phase difference indicates a change in the effective birefringence of the entire polarization–diversity loop, which results in a wavelength shift of the transmission spectrum in the PDLS-based comb filter. In particular, the second WRC composed of HWR 2 and QWR 2 also functions as an effective rotator of HBF 2, which can adjust the effective angular difference between the two principal axes of HBF 1 and HBF 2. Input light incident on port 1 of the PBS is decomposed into linear horizontal polarization (LHP) and linear vertical polarization (LVP) components, which circulate through the polarization–diversity loop of the filter in the clockwise (CW) and counterclockwise (CCW) directions, respectively. If two orthogonally polarized modes propagating along the fast and slow axes of the HBF encounter with each other, having the same state of polarization (SOP) through some polarization conversion components (like wave retarders or polarizers), these orthogonal modes can interfere with the phase delay difference Γ resulting in a periodic interference spectrum. The periodic comb spectrum of our filter is based on this polarization interference defined by Γ = 2πBL/λ, where B, L, and λ are the HBF birefringence, HBF length, and wavelength in vacuum, respectively. Engineered selection of the AOA’s of the wave retarders located before the HBF can create an additional phase difference ψ, resulting in a total phase difference of Γ + ψ. A monotonous change in ψ gives a monotonous wavelength shift in the interference comb spectrum.

As can be found from Figure 1a, the LHP and LVP components emerging from ports 2 and 3 of the PBS are guided in CW and CCW directions, respectively. Here we assume the horizontal and vertical axes of the PBS as x and y axes, respectively, and the direction of light propagation as the z axis for convenience. As seen in Figure 1b, linear horizontally polarized light from port 2 of the PBS goes through a linear horizontal polarizer (i.e., x-axis polarizer), QWR 1 (with its slow axis oriented at θ_Q1 with respect to the x axis), HWR 1 (oriented at θ_H1), HBF 1 (oriented at θ_B1), HWR 2 (oriented at θ_H2), QWR 2 (oriented at θ_Q2), HBF 2 (oriented at θ_B2), and a linear horizontal analyzer (i.e., x-axis polarizer) in turn along the CW path. In a similar way, linear vertically polarized light from port 3 of the PBS passes through a linear vertical polarizer (i.e., y-axis polarizer), HBF 2 (−θ_B2 oriented), QWR 2 (−θ_Q2 oriented), HWR 2 (−θ_H2 oriented), HBF 1 (−θ_B1 oriented), HWR 1 (−θ_H1 oriented), QWR 1 (−θ_Q1 oriented), and a linear vertical analyzer (i.e., y-axis polarizer) in sequence along the CCW path. F and S appearing on the wave retarders and the HBF’s denote their fast and slow axes, respectively. Two orthogonally polarized light (i.e., LHP and LVP components) circulates in the polarization–diversity loop along the CW and CCW paths, respectively. In each path, polarization interference occurs owing to Γ of each HBF, leading to an interference spectrum. Because the input optical power of the filter is distributed to ports 2 and 3 of the PBS according to its input SOP, the insertion losses of these two interference spectra (for the CW and CCW paths) also rely on the input SOP. However, there is no difference in other spectral characteristics of the two interference spectra, for example, a free spectral range (FSR) that determines a channel spacing of the comb filter [17]. This is because the Jones transfer matrices of all the wave retarders and HBF’s used here are lossless and unitary, which can also be confirmed in the following Jones matrix formulation of the filter transmittance. Owing to the orthogonality of the SOP’s of these two interference spectra, the output transmission spectrum of the filter can be obtained by simple arithmetic sum of them. Moreover, as any two orthogonal polarization bases (e.g., LHP and LVP) can generate an arbitrary SOP, the output spectrum is independent of input polarization in our filter [17].

A comb spectrum created by polarization interference has a sinusoidal transmittance function of Γ. As a simple example, the transmittance function of a polarization interference spectrum created in an HBF segment sandwiched by two linear polarizers is represented by p + qcosΓ (where p and q are real constants) called the zeroth-order transmittance function. If the number of the HBF segments inserted between linear polarizers becomes the integer M (≥2), this transmittance function is called the (M−1)-order transmittance function, which includes sinusoidal functions of Γ, such as cos^MΓ, cos^M−1Γ, and cosΓ [25]. To continuously tune the wavelength of a higher-order transmittance function, an extra phase retardation difference ψ should be added to the phase retardation difference Γ of each HBF segment. For this, in view of the transmittance function, (Γ + ψ) should be substituted for Γ in the sinusoidal functions (cos^MΓ, cos^M−1Γ, etc.). As we want to tune a narrowband comb spectrum of the first-order transmittance function (M = 2), the effective phase retardation difference of each HBF segment between linear polarizers needs to become (Γ + ψ) while the effective slow-axis AOA’s of HBF 1 and HBF 2 are set as 22.5° and 67.5°, respectively, as can be found in the CW path of Figure 1c. These two effective AOA’s are inferred by analyzing the AOA relationship between birefringent components in a conventional fan Solc filter with a narrowband transmittance [26]. The extra phase difference ψ and AOA’s (θ_B1 and θ_B2) of HBF can be effectively modified by changing the input polarization of HBF 1 or HBF 2. This input SOP of each HBF can be determined by controlling the AOA’s of the four wave retarders (QWR 1, HWR 1, HWR 2, and QWR 2). If we can set ψ to increase from 0° to 360° through the AOA adjustment of the wave retarders, the narrowband comb spectrum can be continuously red-shifted by a wavelength displacement corresponding to one FSR.

The general transmittance t_filter of our filter can be derived using the Jones transfer matrix T, which contains the transfer matrices of two QWR’s, two HWR’s, two HBF’s, and two polarizers, obtained along the CW and CCW paths, the first and second terms of the right side of (1), respectively. It is assumed here that there is no insertion loss in all the optical components and the wave retarders are frequency-independent.

$$\begin{array}{c}\hfill T=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]T_{HBF2}\left({\theta }_{B2}\right)T_{QWR2}\left({\theta }_{Q2}\right)T_{HWR2}\left({\theta }_{H2}\right)T_{HBF1}\left({\theta }_{B1}\right)T_{HWR1}\left({\theta }_{H1}\right)T_{QWR1}\left({\theta }_{Q1}\right)\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\\ +\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]T_{QWR1}\left(-{\theta }_{Q1}\right)T_{HWR1}\left(-{\theta }_{H1}\right)T_{HBF1}\left(-{\theta }_{B1}\right)T_{HWR2}\left(-{\theta }_{H2}\right)T_{QWR2}\left(-{\theta }_{Q2}\right)T_{HBF2}\left(-{\theta }_{B2}\right)\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right],\end{array}$$

(1)

where T_QWR1, T_HWR1, T_HBF1, T_HWR2, T_QWR2, and T_HBF2 are the Jones transfer matrices of QWR 1, HWR 1, HBF 1, HWR 2, QWR 2, and HBF 2, which have the slow-axis AOA’s of θ_Q1, θ_H1, θ_B1, θ_H2, θ_Q2, and θ_B2 with respect to the x axis, respectively. The Jones transfer matrices (T_QWR, T_HWR, and T_HBF) of a QWR, an HWR, and an HBF, which have the AOA’s of θ_Q, θ_H, and θ_B, respectively, are given as follows.

$$T_{QWR}\left({\theta }_Q\right)=\frac{\sqrt{2}}{2}\left[\begin{array}{cc}1-j\cos 2{\theta }_Q& -j\sin 2{\theta }_Q\\ -j\sin 2{\theta }_Q& 1+j\cos 2{\theta }_Q\end{array}\right],T_{HWR}\left({\theta }_H\right)=-j\left[\begin{array}{cc}\cos 2{\theta }_H& \sin 2{\theta }_H\\ \sin 2{\theta }_H& -\cos 2{\theta }_H\end{array}\right],$$

and

$$T_{HBF}\left({\theta }_B\right)=\left[\begin{array}{cc}\cos \left(\mathsf{\Gamma }/2\right)-j\cos 2{\theta }_B\sin \left(\mathsf{\Gamma }/2\right)& -j\sin 2{\theta }_B\sin \left(\mathsf{\Gamma }/2\right)\\ -j\sin 2{\theta }_B\sin \left(\mathsf{\Gamma }/2\right)& \cos \left(\mathsf{\Gamma }/2\right)+j\cos 2{\theta }_B\sin \left(\mathsf{\Gamma }/2\right)\end{array}\right].$$

(2)

On the basis of (1), t_filter is given by

$$t_{filter}=\frac{1}{4}{\left(P_0+P_1\cos \mathsf{\Gamma }+P_2\sin \mathsf{\Gamma }\right)}^2+\frac{1}{4}{\left(Q_0+Q_1\cos \mathsf{\Gamma }+Q_2\sin \mathsf{\Gamma }\right)}^2.$$

(3)

$$\begin{array}{c}{P}_0=\sin \alpha \sin \beta -\sin \left(\gamma -\frac{\pi }{4}\right)\sin \left(\delta -2{\theta }_{B1}\right),Q_0=\cos \gamma \cos \beta -\cos \left(\alpha +\frac{\pi }{4}\right)\cos \left(\delta -2{\theta }_{B1}\right),\hfill \\ P_1=\sin \alpha \sin \beta +\sin \left(\gamma -\frac{\pi }{4}\right)\sin \left(\delta -2{\theta }_{B1}\right),Q_1=\cos \gamma \cos \beta +\cos \left(\alpha +\frac{\pi }{4}\right)\cos \left(\delta -2{\theta }_{B1}\right),\hfill \\ P_2=\cos \left(\gamma -\frac{\pi }{4}\right)\cos \beta +\cos \alpha \cos \left(\delta -2{\theta }_{B1}\right),\mathrm{and}{Q}_2=-\sin \left(\alpha +\frac{\pi }{4}\right)\sin \beta -\sin \gamma \sin \left(\delta -2{\theta }_{B1}\right),\hfill \end{array}$$

(4)

where α = θ_Q1 – θ_Q2, β = 2θ_H1 – 2θ_H2 – θ_Q1 + θ_Q2, γ = θ_Q1 + θ_Q2, and δ = 2θ_H1 + 2θ_H2 – θ_Q1 – θ_Q2. The narrowband transmittance function t_narrow can be obtained from this general transmittance t_filter and is given by (5), which can also be drawn out in consideration of the transmittance function of a conventional fan Solc filter with two birefringent components (M = 2) [22]. The additional phase difference ψ in t_narrow sets the wavelength position of the narrowband transmission spectrum, that is, can be utilized to tune the spectral location.

$$t_{narrow}=\left[1+2\cos \left(\mathsf{\Gamma }+\psi \right)+{\cos }^2\left(\mathsf{\Gamma }+\psi \right)\right]/4$$

(5)

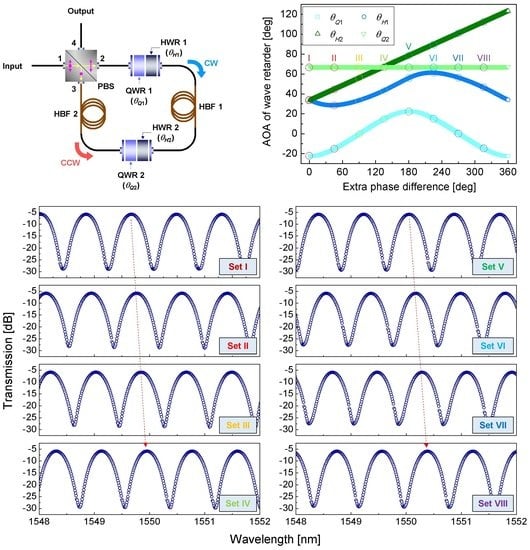
To establish the theoretical conditions of the wave retarders, required to continuously tune the wavelength location of t_narrow, the AOA’s of the four wave retarders, or (θ_Q1, θ_H1, θ_H2, θ_Q2), which could induce ψ’s ranging from 0° to 360° in t_narrow, were investigated by quantitatively comparing (3) with (5). Figure 2a shows the AOA sets of four wave retarders (θ_Q1, θ_H1, θ_H2, θ_Q2), referred hereafter to as four AOA (FAOA) sets, indicated by skyblue squares, blue circles, olive triangles, and green inverted triangles, respectively, for the extra phase difference ψ (from 0° to 360° with a step of 1°), which are found for the continuous wavelength tuning of t_narrow in (5) at θ_B1 = 0°. As ψ increases, θ_Q1 and θ_H1 alternate with ψ at the same frequency, and they are bounded in −22.5° < θ_Q1 < 22.5° and 28.6° < θ_H1 < 61.4°. θ_Q1(ψ) and θ_H1(ψ) seem to have similar alternating trajectories, but they are not sinusoidal functions of ψ. On the other hand, θ_H2 linearly increases with ψ in an AOA range of 33.4° < θ_H2 < 123.5°, and θ_Q2 is not a function of ψ but a constant value of 67.5°. From Figure 2a, we can clearly see that an FAOA set (θ_Q1, θ_H1, θ_H2, θ_Q2) corresponds to any ψ increasing from 0° to 360° with a step of 1°. This means that the narrowband transmittance t_narrow can be wavelength-tuned if an FAOA set is picked along these four trajectories of θ_Q1(ψ), θ_H1(ψ), θ_H2(ψ), and θ_Q2(ψ) so that ψ increases from 0° to 360°. Moreover, it can effortlessly be confirmed from quantitative calculations that the same locus is obtained for each trajectory shown in Figure 2a, even for ψ with 360 or more steps split at an angle smaller than 1°, which proves once again the continuous frequency tunability of t_narrow in our filter. In the case of θ_B1 ≠ 0°, θ_H1 and θ_H2 are simultaneously increased by θ_B1/2 for all ψ.

Figure 2b,c show four types of loci of (θ_Q1, θ_H1) and (θ_H2, θ_Q2), which are plotted for ψ (from 0° to 360°) at θ_B1 = 0° in the Cartesian coordinate systems of (θ_Q1, θ_H1) and (θ_H2, θ_Q2), respectively. There are four types of FAOA sets that can implement the continuous frequency tuning of the narrowband spectrum, and the AOA sets represented in Figure 2a show one of them. In Figure 2b, four subplots displayed as Types I to IV, that is, the four loci of (θ_Q1, θ_H1), show Lissajous trajectories plotted using both θ_Q1(ψ) and θ_H1(ψ) in these four types of FAOA sets. Similarly, in Figure 2c, four subplots denoted by Types I to IV, i.e., the four loci of (θ_H2, θ_Q2), are obtained using both θ_H2(ψ) and θ_Q2(ψ) in the four types of FAOA sets. In Figure 2b,c, the locus plots of Types I to IV are indicated by blue circles, green squares, red triangles, and violet inverted triangles, respectively. Among the four types of loci, two Type I loci in Figure 2b,c are drawn out from θ_Q1(ψ) and θ_H1(ψ) traces and θ_H2(ψ) and θ_Q2(ψ) traces in Figure 2a, respectively. In terms of Types I and II loci in Figure 2b, the point of (θ_Q1, θ_H1) on the elliptical locus moves CCW along the locus, starting at a void circle and a void square, respectively, while ψ increases from 0° to 360°. As opposed to the former case, in the case of Types III and IV loci in Figure 2b, the point of (θ_Q1, θ_H1) moves CW along the locus, starting at a void triangle and a void inverted triangle, respectively, with increasing ψ from 0° to 360°. In particular, the elliptical locus of Type I is determined by the following relations (6) and (7), which can be derived by considering the ψ-driven evolution of the output SOP of HWR 1 on the Poincare sphere [22].

$$\tan \left(4{\theta }_{H1}-2{\theta }_{Q1}\right)=\frac{\sin 2{\theta }_{B1}-\cos 2{\theta }_{B1}\sin \psi }{\cos 2{\theta }_{B1}+\sin 2{\theta }_{B1}\sin \psi }$$

(6)

and

$$\sin 2{\theta }_{Q1}=-\frac{1}{\sqrt{2}}\cos \psi$$

(7)

These simple and deterministic locus patterns pave the way for easy prediction of FAOA sets for the continuous wavelength tuning of narrowband spectra. For Types I and III loci in Figure 2c, the point of AOA’s (θ_H2, θ_Q2) on the linear locus goes from left to right with θ_Q2 maintained as 67.5°, as ψ increases from 0° to 360°. On the contrary, for Types II and IV loci in Figure 2c, the point of (θ_H2, θ_Q2) on the locus shifts from right to left keeping θ_Q2 = 157.5° with the increase of ψ from 0° to 360°. To grasp the total loci at a glance, as shown in Figure 2d, we plotted the four loci of (θ_Q1, θ_H1, θ_H2) with respect to ψ (from 0° to 360°) at θ_B1 = 0° in the Cartesian coordinate system of θ_Q1, θ_H1, and θ_H2, using θ_Q1(ψ), θ_H1(ψ), and θ_H2(ψ) shown in Figure 2a. To maintain consistency, the locus plots of Types I to IV are indicated by blue circles, green squares, red triangles, and violet inverted triangles, respectively, as in Figure 2b,c. In terms of Types I and III loci (θ_Q2 = 67.5°), the point of AOA’s (θ_Q1, θ_H1, θ_H2) on these helical loci rises from the bottom with the increase of ψ (from bright to dark markers). In contrast, for Types II and IV loci (θ_Q2 = 157.5°), the point of (θ_Q1, θ_H1, θ_H2) on the loci comes down from the top with increasing ψ. For each type of locus, eight points indicated by I to VIII show the eight sets of FAOA’s selected to spectrally shift t_narrow. From set I to set VIII, an additional phase difference ψ increases from 0° to 315° with a step of 45°. In other words, if we put the FSR of the narrowband transmission spectrum as Δλ, the narrowband transmission spectrum at set I is red-shifted by Δλ/8, Δλ/4, 3Δλ/8, Δλ/2, 5Δλ/8, 3Δλ/4, and 7Δλ/8 at sets II to VIII, respectively.

3. Spectral Calculation and Experimental Demonstration

Figure 3 shows the calculated narrowband transmission spectra of the proposed filter, obtained at the eight selected FAOA sets (sets I to VIII) over the wavelength range from 1548 to 1552 nm. In this spectrum calculation, the length L and birefringence B of each HBF (HBF 1 or HBF 2) were set as 7.2 m and 4.166 × 10⁻⁴ to make Δλ of the narrowband spectrum become ~0.8 nm at 1550 nm, respectively. As can be checked from the figure, the narrowband spectrum moves towards a longer wavelength region as the FAOA set changes from set I to set VIII. If one peak wavelength of the comb spectrum at set I is denoted by λ₀ (=1550.4 nm), as shown in the left-top subplot of Figure 3, λ₀ increases from 1550.5 to 1551.1 nm by 0.1 nm per set, while the FAOA set switches from set II to set VIII. In particular, it was also confirmed through additional spectral calculations that λ₀ linearly increased with ψ for finer values of ψ (for instance, 360 values of ψ starting from 0° with a step of 1°), although the calculation results were not provided here. This implies that the narrowband comb spectrum can be continuously tuned in its wavelength. As a result, this calculated result corroborates that our comb filter can be continuously frequency-tuned within Δλ by properly selecting FAOA sets. For experimental demonstration of the calculated results, an actual implementation of our filter was done by incorporating a PBS (OZ Optics) pigtailed with single-mode fiber (SMF), two SMF-pigtailed QWR’s (OZ Optics), two SMF-pigtailed HWR’s (OZ Optics), and two equal-length bow-tie HBF segments (Fibercore), as shown in Figure 1. Considering the birefringence (~4.166 × 10⁻⁴) of the HBF, its length was tailored to be ~7.12 m so that Δλ became ~0.8 nm at 1550 nm. The transmission spectra of the constructed filter were measured using a broadband light source (Fiberlabs FL7701) and an optical spectrum analyzer (Yokogawa AQ6370C). Figure 4 shows an actual experimental setup for measurement of the transmission spectra of the filter. As shown in Figure 4, the input and output ports (ports 1 and 4) of the filter were connected to the broadband light source and optical spectrum analyzer, respectively, with FC/PC type fiber patchcords. The sensitivity and resolution bandwidth of the optical spectrum analyzer were set as HIGH1 and 0.02 nm, respectively, to acquire high resolution and high contrast optical spectra. To avoid unwanted displacements of all the optical components of the filter, we taped them up on the optical table so that they were immobilized during the spectrum measurement.

Figure 5 shows the narrowband transmission spectra, measured at the eight FAOA sets (sets I to VIII) in

Table 1. Eight selected sets of FAOA’s for wavelength tuning of the constructed filter.

Set	FAOA’s
	θQ1	θH1	θH2	θQ2
I	94°	56°	22°	62°
II	112°	58°	28°	72°
III	120°	72°	36°	80°
IV	140°	80°	50°	84°
V	178°	60°	46°	80°
VI	36°	38°	20°	10°
VII	60°	56°	26°	44°
VIII	80°	68°	30°	62°

. The resolution bandwidth of the optical spectrum analyzer was 0.05 nm during the measurement. For the eight comb spectra, the average insertion loss was measured to be ~5.88 dB and primarily attributed to the insertion losses of the PBS and wave retarders and the fiber splicing losses between different types of fibers (e.g., HBF and SMF). When we sequentially switched the FAOA set from set I to set VIII, the narrowband transmission spectrum moved towards a longer wavelength region by ~0.1 nm, leading to an entire wavelength shift of ~0.7 nm.

Figure 6a shows the variation of the peak wavelength denoted by λ₀ in Figure 5, measured at the eight FAOA sets. A skyblue solid line indicates a linear fit of the measured data of λ₀. As can be figured out from the figure, λ₀ and ψ have a highly linear relationship. From this linear fit, the adjusted R² value was evaluated as ~0.99723. It was also found that any desirable ψ values between 0° and 360°, in addition to integer multiples of 45°, could be obtained by choosing appropriate FAOA’s. Thus, it is experimentally confirmed that the narrowband transmission spectrum can be continuously wavelength-tuned by elaborately adjusting FAOA sets of (θ_Q1, θ_H1, θ_H2, θ_Q2). Figure 6b shows two superimposed plots of eight narrowband transmission spectra measured at the eight FAOA sets over a wavelength range from 1545 to 1555 nm; the upper plot displays four narrowband transmission spectra measured at the FAOA sets I, III, V, and VII, and the lower plot displays four narrowband transmission spectra measured at the FAOA sets II, IV, VI, and VIII. It is observed from the figure that the insertion losses are nearly even and the spectral flatness between transmission channels is less than 0.13 dB over the entire spectral range (10 nm). Moreover, the extinction ratio was measured to be more than 20 dB over the same wavelength range.

4. Conclusions

In summary, we proposed and experimentally demonstrated a narrowband wavelength-tunable fiber comb filter based on the PDLS with composite combination of wave retarders. The demonstrated filter is comprised of a PBS, two HBF segments of the same length, an ordered WRC of a QWR and an HWR before the first HBF segment, and an ordered WRC of an HWR and a QWR before the second HBF segment. The second HBF segment is butt-coupled to one port of the PBS so that its slow axis should be oriented at 22.5° with respect to the horizontal axis of the PBS. Through this butt-coupling between the second HBF segment and the PBS, one HWR for the spectrum visibility can be eliminated compared with the recent previous works [23,24]. By comparing the narrowband transmittance function t_narrow with the filter transmittance t_filter obtained by Jones matrix formulation, we found the AOA sets of the four wave retarders, which could give additional phase shifts (ψ’s) from 0° to 360° to t_narrow. From comb spectra calculated at the eight selected FAOA sets, which cause ψ to increase from 0° to 315° by a step of 45°, it is confirmed that the first-order narrowband comb spectrum can be continuously tuned by properly adjusting the AOA’s, which clearly indicates the continuous wavelength tunability of the proposed filter adopting composite combination of ordered wave retarders. The validity of our calculation results were examined by actually implementing the proposed filter and confirmed by appropriately choosing the AOA of each wave retarder. Then, it is concluded that our filter employing the composite combination of wave retarders can be continuously wavelength-tuned by properly controlling the AOA’s of the wave retarders. Primary optical components comprising the proposed filter, including a PBS, four wave retarders, and HBF, can be implemented in an integrated form [27,28,29], and thus the filter can be utilized as an integrated optical communication element in fiber-optic networks. Our wavelength-tunable narrowband comb filter is anticipated to be beneficially utilized in microwave photonic signal processing, optical sensor interrogation, and multiwavelength lasing. Some points to be considered for the use of our filter in practical applications are the wavelength dependency of the wave retarders and the temperature dependence of the HBF birefringence. Achromatic wave retarders can resolve this wavelength dependency. In terms of the temperature dependence, hermetical sealing or packaging of HBF segments can facilitate their temperature insensitivity, and, furthermore, a thermoelectric cooler can also be employed for stabilization of the HBF birefringence.