Intelligent Diagnosis of Rotating Machinery Based on Optimized Adaptive Learning Dictionary and 1DCNN
Abstract
:1. Introduction
- (1)
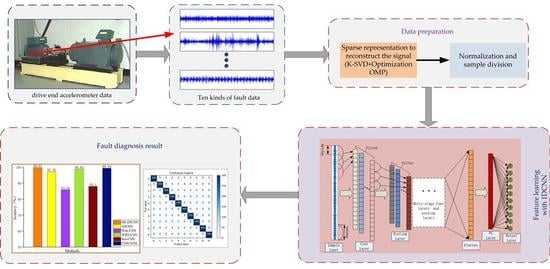
- An intelligent fault diagnosis method based on optimized adaptive learning dictionary and convolution neural network is proposed. The original signal is sparsely reconstructed directly by using adaptive learning dictionary and used as the input of 1DCNN, which reduces the interference of noise to a great extent and fully retains the characteristic information at the same time.
- (2)
- Through the use of various techniques such as data enhancement and batch normalization, the robustness and generalization ability of the network model in different noise environments are improved. This method is more suitable for accurate and effective fault classification and diagnosis.
- (3)
- By using the bearing dataset of CWRU and the experimental dataset of the worm gear reducer of Shanghai University of Technology, it is proved that this method has better diagnosis accuracy and provides a better solution for the fault diagnosis of rotating machinery.
2. Sparse Representation
2.1. Construction of Redundant Dictionary
| Algorithm 1. The specific steps of the K-SVD algorithm |
| Step 1: Initialize the dictionary , and randomly select column vectors from the original sample as the atoms of the initial dictionary. Then, set the relevant parameters: sample length , number of iterations , and sparsity . Step 2: Fixed dictionary , using a sparse coefficient algorithm to solve : Step 3: Fixed sparse coefficient , update the dictionary column by column ; when the is updated, the residual matrix is calculated : Step 4: Repeat steps 2 and 3 until the iterative conditions are met. |
2.2. Sparse Coefficient Solution
| Algorithm 2. The steps |
Input: Sample , Sparsity k, Training Dictionary .
|
3. One-Dimensional Convolution Neural Network (1DCNN)
3.1. Convolution Layer
3.2. Activation Layer
3.3. Pooling Layer
3.4. Full Connection Layer
4. Proposed Intelligent Fault Diagnosis Method
- (1)
- The original vibration signal collected by the sensor is sparsely represented and normalized, and the training set, verification set, and test set are divided according to a certain proportion.
- (2)
- Construct one-dimensional convolution neural network and set relevant network parameters: iterative steps, training batches, convolution layers, and convolution kernel size, number, and step size of each layer.
- (3)
- Initialize the network parameters, input the training samples into the 1DCNN network in batches, and begin to perform the forward propagation of the model. The output layer obtains the accuracy and calculates the error.
- (4)
- Carry on the back propagation algorithm to the error, update the weight, and offset until the network training is completed.
- (5)
- Input the test set into the trained model, output the classification accuracy, and evaluate the classification effect.
5. Experiment Verification and Analysis
5.1. Experiment on Datasets of Rolling Bearing in Case Western Reserve University
5.1.1. Experiment Description
5.1.2. Optimization Selection of the SR−1DCNN Model
- (1)
- Sparse representation selection of related parameters
- (2)
- Parameter selection of 1DCNN Network Model
5.1.3. Data Enhancement
5.1.4. Analyze the Process and Results
5.2. Dataset Experiment of Worm Gear Reducer
5.2.1. Experimental Description
5.2.2. Analysis Process and Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.J.; Zhou, J.; Wang, J.Y.; Du, W.H.; Wang, J.T.; Han, X.F.; He, G.F. A novel fault diagnosis method of gearbox based on maximum kurtosis spectral entropy deconvolution. IEEE Access 2019, 7, 29520–29532. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.X.; Wang, S.Q.; Li, W.H.; Thompson, S.G.; Feng, S.Z. A Hybrid Deep-Learning Model for Fault Diagnosis of Rolling Bearings. Measurement 2021, 169, 108502. [Google Scholar] [CrossRef]
- Wu, J.; Wu, C.Y.; Cao, S.; Or, S.W.; Deng, C.; Shao, X.Y. Degradation data-driven time-to-failure prognostics approach for rolling element bearings in electrical machines. IEEE Trans. Ind. Electron. 2019, 66, 529–539. [Google Scholar] [CrossRef]
- Cerrada, M.; Sánchez, R.V.; Li, C.; Pacheco, F.; Cabrera, D.; Oliveira, J.V.D.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Jiang, G.Q.; He, H.B.; Yan, J.; Xie, P. Multiscale convolutional neural networks for fault diagnosis of wind turbine gearbox. IEEE Trans. Ind. Electron. 2018, 66, 3196–3207. [Google Scholar] [CrossRef]
- Xiao, M.H.; Wen, K.; Zhang, C.Y.; Zhao, X.; Wei, W.H.; Wu, D. Research on Fault Feature Extraction Method of Rolling Bearing Based on NMD and Wavelet Threshold Denoising. Shock. Vib. 2018, 2018, 9495265. [Google Scholar] [CrossRef]
- Abdelkader, R.; Kaddour, A.; Derouiche, Z. Enhancement of rolling bearing fault diagnosis based on improvement of empirical mode decomposition denoising metho. Int. J. Adv. Manuf. Technol. 2018, 97, 3099–3117. [Google Scholar] [CrossRef]
- Wang, P.; Wang, T.Y. Energy weighting method and its application to fault diagnosis of rolling bearing. J. Vibroeng. 2017, 19, 223–236. [Google Scholar] [CrossRef]
- Alexakos, C.T.; Karnavas, Y.L.; Drakaki, M.; Tziafettas, I.A. A Combined Short Time Fourier Transform and Image Classification Transformer Model for Rolling Element Bearings Fault Diagnosis in Electric Motors. Mach. Learn. Knowl. Extr. 2021, 3, 11. [Google Scholar] [CrossRef]
- Yi, Q. A New Family of Model-Based Impulsive Wavelets and Their Sparse Representation for Rolling Bearing Fault Diagnosis. IEEE Trans. Ind. Electron. 2018, 65, 2716–2726. [Google Scholar]
- Wang, L.; Cai, G.G.; Gao, G.Q.Z.F.; Yang, S.Y.; Zhu, Z.K. Fast algorithm of sparse representation based on improved MP and its application of rolling bearing fault feature extraction. Vib. Shock. 2017, 36, 176–182. [Google Scholar]
- Hou, F.T.; Chen, J.; Dong, G.M. Weak fault feature extraction of rolling bearings based on globally optimized sparse coding and approximate SVD. Mech. Syst. Signal Process. 2018, 111, 234–250. [Google Scholar] [CrossRef]
- Li, J.M.; Li, M.; Yao, X.F.; Wang, H.; Yu, Q.W.; Wang, X.D. Rolling bearing fault diagnosis based on ensemble empirical mode decomposition and k-singular value decomposition dictionary learning. Acta Metrol. Sin. 2020, 41, 1260–1266. [Google Scholar]
- Yang, H.G.; Lin, H.B.; Ding, K. Sliding window denoising K-Singular Value Decomposition and its application on rolling bearing impact fault diagnosis. J. Sound Vib. 2018, 421, 205–219. [Google Scholar] [CrossRef]
- Zeng, M.; Zhang, W.M.; Chen, Z. Group-Based K-SVD Denoising for Bearing Fault Diagnosis. IEEE Sens. J. 2019, 99, 1. [Google Scholar] [CrossRef]
- Lu, W.; Song, L.Y.; Cui, L.L.; Wang, H.Q. A Novel Weak Fault Diagnosis Method Based on Sparse Representation and Empirical Wavelet Transform for Rolling Bearing. In Proceedings of the 2020 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Xi’an, China, 15–17 October 2020. [Google Scholar]
- Wang, Z.Y.; Yao, L.G.; Cai, Y.W. Rolling bearing fault diagnosis using generalized refined composite multiscale sample entropy and optimized support vector machine. Measurement 2020, 156, 107574. [Google Scholar] [CrossRef]
- Wang, H.Y.; Yu, Z.Q.; Guo, L. Real-time Online Fault Diagnosis of Rolling Bearings Based on KNN Algorithm. J. Phys. Conf. Ser. 2020, 1486, 032019. [Google Scholar] [CrossRef]
- Li, J.M.; Yao, X.F.; Wang, X.D.; Yu, Q.W.; Zhang, Y.G. Multiscale local features learning based on BP neural network for rolling bearing intelligent fault diagnosis. Measurement 2020, 153, 107419. [Google Scholar] [CrossRef]
- Peng, D.D.; Wang, H.; Liu, Z.L.; Zhang, W.; Zuo, M.J.; Chen, J. Multi-branch and Multi-scale CNN for Fault Diagnosis of Wheelset Bearings under Strong Noise and Variable Load Condition. IEEE Trans. Ind. Inform. 2020, 16, 4949–4960. [Google Scholar] [CrossRef]
- Wen, L.; Li, X.Y.; Gao, L.; Zhang, Y.Y. A New Convolutional Neural Network-Based Data-Driven Fault Diagnosis Method. IEEE Trans. Ind. Electron. 2018, 65, 5990–5998. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.; Qin, X.R.; Sun, Y.T. Fault diagnosis method for rolling bearings based on short-time Fourier transform and convolutional neural network. J. Vib. Shock. 2018, 37, 124–131. [Google Scholar]
- Liu, R.N.; Wang, F.; Yang, B.Y.; Qin, S.J. Multiscale Kernel Based Residual Convolutional Neural Network for Motor Fault Diagnosis Under Nonstationary Conditions. IEEE Trans. Ind. Inform. 2020, 16, 3797–3806. [Google Scholar] [CrossRef]
- Yang, Y.H.; Li, D.L.; Liu, X.Z. Fault Diagnosis Based On One-Dimensional Deep Convolution Neural Network. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC) IEEE, Hefei, China, 22–24 August 2020. [Google Scholar]
- Zhang, A.S.; Li, S.B.; Cui, Y.X.; Yang, W.; Dong, R.; Hu, J. Limited Data Rolling Bearing Fault Diagnosis With Few-Shot Learning. IEEE Access 2019, 7, 110895–110904. [Google Scholar] [CrossRef]
- Qin, C.J.; Jin, Y.R.; Tao, J.F.; Yang, W.L.; Dong, R.Z.; Hu, J.J. DTCNNMI: A deep twin convolutional neural networks with multi-domain inputs for strongly noisy diesel engine misfire detection. Measurement 2021, 180, 109548. [Google Scholar] [CrossRef]
- Xue, Y.; Dou, D.Y.; Yang, J.G. Multi-fault diagnosis of rotating machinery based on deep convolution neural network and support vector machine. Measurement 2020, 156, 107571. [Google Scholar] [CrossRef]
- Ji, M.Y.; Peng, G.L.; He, J.; Liu, S.H.; Chen, Z.; Li, S.J. A Two-Stage, Intelligent Bearing-Fault-Diagnosis Method Using Order-Tracking and a One-Dimensional Convolutional Neural Network with Variable Speeds. Sensors 2021, 21, 675. [Google Scholar] [CrossRef]
- Peng, D.D.; Liu, Z.L.; Wang, H.; Qin, Y.; Jia, L.M. A novel deeper one-dimensional CNN with residual learning for fault diagnosis of wheelset bearings in high-speed trains. IEEE Access 2018, 7, 10278–10293. [Google Scholar] [CrossRef]
- He, K.M.; Sun, J. Convolutional neural networks at constrained time cost. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5353–5360. [Google Scholar]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Olshausen, B.A.; Field, D.J. Emergence of imple-cell receptive field properties by learning a sparse code for natural images. Nature 1996, 381, 607–609. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhao, C.; Zhao, D.B.; Gao, W. Image compressive sensing recovery using adaptively learned sparsifying basis via L0 minimization. Signal Process. 2014, 103, 114–126. [Google Scholar] [CrossRef] [Green Version]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery from Random Measurements Via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Cai, G.G.; You, W.; Huang, W.G.; Zhu, Z.K. Transients Extraction Based on Averaged Random Orthogonal Matching Pursuit Algorithm for Machinery Fault Diagnosis. IEEE Trans. Instrum. Meas. 2017, 66, 3237–3248. [Google Scholar] [CrossRef]
- Tang, S.G.; Yuan, S.Q.; Zhu, Y. Convolutional Neural Network in Intelligent Fault Diagnosis toward Rotatory Machinery. IEEE Access 2020, 8, 86510–86519. [Google Scholar] [CrossRef]
- Liang, P.F.; Deng, C.; Wu, J.; Yang, Z.X. Intelligent fault diagnosis of rotating machinery via wavelet transform, generative adversarial nets and convolutional neural network. Measurement 2020, 159, 107768. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Ide, H.; Kurita, T. Improvement of learning for CNN with ReLU activation by sparse regularization. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 2684–2691. [Google Scholar]
- Huang, S.Z.; Tang, J.; Dai, J.Y.; Wang, Y.Y.; Dong, J.J. 1DCNN Fault Diagnosis Based on Cubic Spline Interpolation Pooling. Shock. Vib. 2020, 2020, 1949863. [Google Scholar] [CrossRef] [Green Version]
- Case Western Reserve University Bearing Data Center. Available online: https://csegroups.case.edu/bearingdatacenter/home (accessed on 15 August 2021).
- Akata, Z.; Perronnin, F.; Harchaoui, Z.; Schmid, C. Label-Embedding for Image Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 1425–1438. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Peng, G.L.; Li, C.H.; Chen, Y.H.; Zhang, Z.J. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Chen, L.L.; Fu, Z.C.; Ling, J.; Dong, S.J. Fault diagnosis of rolling bearing based on WPD-CNN two-dimensional time-frequency image. Modul. Mach. Tool Autom. Mach. Technol. 2021, 3, 57–61. [Google Scholar]
- Han, T.; Zhang, L.W.; Yin, Z.J.; Tan, A.C.C. Rolling bearing fault diagnosis with combined convolutional neural networks and support vector machine. Measurement 2021, 177, 109022. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ding, Q. Deep residual learning-based fault diagnosis method for rotating machinery. ISA Trans. 2019, 95, 295–305. [Google Scholar] [CrossRef]
- Wang, S.Y. Research on Key Technologies of Wind Turbine Health Monitoring and Evaluation; Shanghai Jiaotong University: Shanghai, China, 2017. [Google Scholar]
- Liu, H.N.; Liu, C.L.; Huang, Y.X. Adaptive feature extraction using sparse coding for machinery fault diagnosis. Mech. Syst. Signal Process. 2011, 25, 558–574. [Google Scholar] [CrossRef]



















| Fault Location | Normal | Ball (B) | Inner Race (IR) | Outer Race (OR) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Category labels | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Fault diameter | 0 | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 | 0.007 | 0.014 | 0.021 |
| Sample length | 2048 | 2048 | 2048 | 2048 | 2048 | 2048 | 2048 | 2048 | 2048 | 2048 |
| Load (hp) | 0,1,2,3 | 0,1,2,3 | 0,1,2,3 | 0,1,2,3 | 0,1,2,3 | 0,1,2,3 | 0,1,2,3 | 0,1,2,3 | 0,1,2,3 | 0,1,2,3 |
| Training sample | 600 | 600 | 600 | 600 | 600 | 600 | 600 | 600 | 600 | 600 |
| Validation sample | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Testing sample | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 | 300 |
| Network Layer | Kernel Number | Kernel Size | Kernel Stride |
|---|---|---|---|
| Convolution layer 1 | 16 | 16 | 2 |
| Pooling layer 1 | 16 | 2 | 2 |
| Convolution layer 2 | 32 | 3 | 1 |
| Pooling layer 2 | 32 | 2 | 2 |
| Convolution layer 3 | 64 | 3 | 1 |
| Pooling layer 3 | 64 | 2 | 2 |
| Convolution layer 4 | 64 | 3 | 1 |
| Pooling layer 4 | 64 | 2 | 2 |
| Convolution layer 5 | 64 | 3 | 1 |
| Pooling layer 5 | 64 | 2 | 2 |
| Fully connection | 1 | 100 | — |
| Softmax | 1 | 10 | — |
| Fault Location | Normal | Pitting | Spalling | Breaking |
|---|---|---|---|---|
| Category labels | 0 | 1 | 2 | 3 |
| Sample length | 2048 | 2048 | 2048 | 2048 |
| Load (Nm) | 0.6 | 0.6 | 0.6 | 0.6 |
| Training sample | 600 | 600 | 600 | 600 |
| Validation sample | 100 | 100 | 100 | 100 |
| Testing sample | 300 | 300 | 300 | 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Liu, C.; Du, W.; Wang, S. Intelligent Diagnosis of Rotating Machinery Based on Optimized Adaptive Learning Dictionary and 1DCNN. Appl. Sci. 2021, 11, 11325. https://doi.org/10.3390/app112311325
Wang H, Liu C, Du W, Wang S. Intelligent Diagnosis of Rotating Machinery Based on Optimized Adaptive Learning Dictionary and 1DCNN. Applied Sciences. 2021; 11(23):11325. https://doi.org/10.3390/app112311325
Chicago/Turabian StyleWang, Hongchao, Chuang Liu, Wenliao Du, and Shuangyuan Wang. 2021. "Intelligent Diagnosis of Rotating Machinery Based on Optimized Adaptive Learning Dictionary and 1DCNN" Applied Sciences 11, no. 23: 11325. https://doi.org/10.3390/app112311325
APA StyleWang, H., Liu, C., Du, W., & Wang, S. (2021). Intelligent Diagnosis of Rotating Machinery Based on Optimized Adaptive Learning Dictionary and 1DCNN. Applied Sciences, 11(23), 11325. https://doi.org/10.3390/app112311325