A Self-Testing Platform with a Foreground Digital Calibration Technique for SAR ADCs
Abstract
:1. Introduction
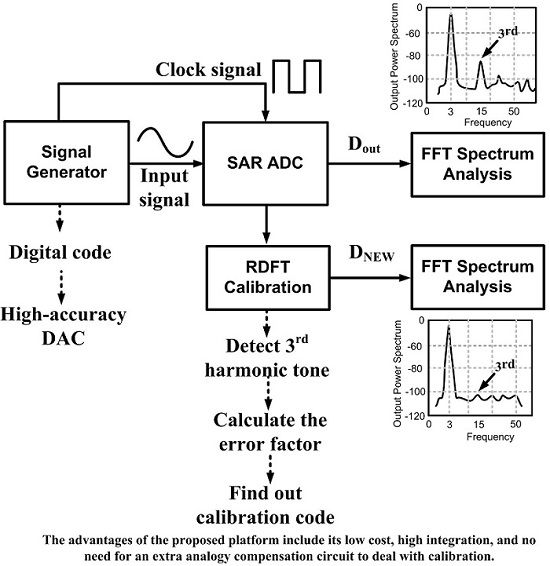
2. Proposed Self-Test Platform
2.1. Conventional SAR ADC Architecture
2.2. Proposed Calibration Method
2.3. MATLAB Verification
2.4. Testing Stimulus Signal
2.5. RDFT Design
2.6. Processing Flow of the Proposed Self-Testing Platform
2.7. Proposed Platform Design
3. Measurement Results
3.1. Multi-Mode SAR ADC
3.2. Proposed Self-Testing Platform
4. Conclusion and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zou, X.; Xu, X.; Yao, L.; Lian, Y. A 1-V 450-nW fully integrated programmable biomedical sensor interface chip. IEEE J. Solid-State Circuits. 2009, 44, 1067–1077. [Google Scholar] [CrossRef]
- Nakane, H.; Ujiie, R.; Oshima, T.; Yamamoto, T.; Kimura, K.; Okuda, Y.; Tsuiji, K.; Matsuura, T. Afully integrated SAR ADC using digital correction technique for triple-mode mobile transceiver. IEEE J. Solid-State Circuits. 2014, 49, 2503–2514. [Google Scholar] [CrossRef]
- Balestrieri, E.; Daponte, P.; Rapuano, S. A state of the art on ADC error compensation methods. IEEE Trans. Instrum. Meas. 1987, 54, 1388–1394. [Google Scholar] [CrossRef]
- Chang, H.M.; Lin, K.Y.; Cheng, K.T. Tester-assisted calibration and screening for digitally-calibrated ADCs. IEEE Trans. Circuits Syst. I Reg. Pap. 2011, 58, 2838–2848. [Google Scholar] [CrossRef]
- Schmidt, C.A.; Lifschitz, O.; Cousseau, J.E.; Figueroa, J.L.; Julián, P. Methodology and measurement setup for analog-to-digital converter postcompensation. IEEE Trans. Instrum. Meas. 2014, 63, 658–666. [Google Scholar] [CrossRef]
- Wang, G.; Kacani, F.; Chiu, Y. IRD digital background calibration of SAR ADC with coarse reference ADC acceleration. IEEE Trans. Circuits Sys. II: Exp. Briefs. 2014, 61, 11–15. [Google Scholar] [CrossRef]
- Liang, M.C.; Hsieh, C.H.; Lee, S.Y. A 1.5-bit/stage pipelined ADC with FFT-based calibration method. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013.
- Juan, Y.H.; Huang, H.Y.; Lai, S.C.; Juang, W.H.; Lee, S.Y.; Luo, C.H. A distortion cancelation technique with the recursive DFT method for successive approximation analog-to-digital converter. IEEE Trans. Circuits Sys. II Exp. Briefs. 2016, 63, 146–150. [Google Scholar] [CrossRef]
- Chang, H.W.; Huang, H.Y.; Juan, Y.H.; Wang, W.S.; Luo, C.H. Adaptive successive approximation ADC for biomedical acquisition system. Microelectron. J. 2013, 44, 729–735. [Google Scholar] [CrossRef]
- Burns, M.; Roberts, G.W. An introduction to mixed-signal IC test and measurement; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Lai, S.C.; Lei, S.F.; Chang, C.L.; Lin, C.C.; Luo, C.H. Low computational complexity, low power, and low area design for the implementation of recursive DFT and IDFT algorithms. IEEE Trans. Circuits Sys. II Exp. Briefs. 2009, 56, 921–925. [Google Scholar] [CrossRef]
- Thirunakkarasu, S.; Bakkaloglu, B. Built-in self-calibration and digital-trim technique for 14-bit SAR ADCs achieve ±1 LSB INL. IEEE Trans. Very Large Scale Integr. (VLSI) Sys. 2015, 23, 916–925. [Google Scholar] [CrossRef]
- Xu, R.; Liu, B.; Yuan, J. Digitally calibrated 768-kS/s 10-b minimum-size SAR ADC array with dithering. IEEE J. Solid-State Circuits. 2012, 47, 1–12. [Google Scholar] [CrossRef]
- Um, J.Y.; Kim, Y.J.; Song, E.W.; Sim, J.Y.; Park, H.J. A digital-domain calibration of split-capacitor DAC for a differential SAR ADC without additional analog circuits. IEEE Trans. Circuits Syst. I Reg. Pap. 2013, 60, 2845–2856. [Google Scholar] [CrossRef]



















| JSSCC'12 [13] | TCASI,13 [14] | TVLSI,15 [12] | This work | |
|---|---|---|---|---|
| Technology | 0.18 µm | 0.13 µm | 0.6 µm | 0.18 µm |
| Method | Dither | Split-CDAC | CDAC | RDFT |
| Supply voltage | 3.3 V (analog) 1.8 V (digital) | 0.5 V | 15 V | 3.3 V (digital) 1.8 V (analog) |
| Resolution | 10 bit | 11 bit | 14 bit | 12 bit |
| Sampling rate | 768 kS/s | 10 kS/s | 400 kS/s | 18.75 kS/s |
| SNDR (dB) (Wo/Wi) | 49.7/60.9 | 56.5/61.6 | 61.2/73.3 | 55.0/61.35 |
| ENOB (bit) (Wo/Wi) | 7.96/9.83 | 9.09/9.93 | 9.88/11.9 | 8.88/9.89 |
| Power (analog) | 58 μW | 0.56 μW | 90 mW | 41.5 μW |
| Area | 10.6 mm2 | 0.58 mm2 | 9.76 mm2 (only ADC) | 2.38 mm2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juan, Y.-H.; Huang, H.-Y.; Lee, S.-Y.; Lai, S.-C.; Juang, W.-H.; Luo, C.-H. A Self-Testing Platform with a Foreground Digital Calibration Technique for SAR ADCs. Appl. Sci. 2016, 6, 217. https://doi.org/10.3390/app6080217
Juan Y-H, Huang H-Y, Lee S-Y, Lai S-C, Juang W-H, Luo C-H. A Self-Testing Platform with a Foreground Digital Calibration Technique for SAR ADCs. Applied Sciences. 2016; 6(8):217. https://doi.org/10.3390/app6080217
Chicago/Turabian StyleJuan, Yi-Hsiang, Hong-Yi Huang, Shuenn-Yuh Lee, Shin-Chi Lai, Wen-Ho Juang, and Ching-Hsing Luo. 2016. "A Self-Testing Platform with a Foreground Digital Calibration Technique for SAR ADCs" Applied Sciences 6, no. 8: 217. https://doi.org/10.3390/app6080217
APA StyleJuan, Y. -H., Huang, H. -Y., Lee, S. -Y., Lai, S. -C., Juang, W. -H., & Luo, C. -H. (2016). A Self-Testing Platform with a Foreground Digital Calibration Technique for SAR ADCs. Applied Sciences, 6(8), 217. https://doi.org/10.3390/app6080217