A Multiple-Model Particle Filter Fusion Algorithm for GNSS/DR Slide Error Detection and Compensation

Abstract

Continuous accurate positioning is a key element for the deployment of many advanced driver assistance systems (ADAS) and autonomous vehicle navigation. To achieve the necessary performance, global navigation satellite systems (GNSS) must be combined with other technologies. A common onboard sensor-set that allows keeping the cost low, features the GNSS unit, odometry, and inertial sensors, such as a gyro. Odometry and inertial sensors compensate for GNSS flaws in many situations and, in normal conditions, their errors can be easily characterized, thus making the whole solution not only more accurate but also with more integrity. However, odometers do not behave properly when friction conditions make the tires slide. If not properly considered, the positioning perception will not be sound. This article introduces a hybridization approach that takes into consideration the sliding situations by means of a multiple model particle filter (MMPF). Tests with real datasets show the goodness of the proposal.

1. Introduction

Today’s most outstanding technology for road vehicle positioning is global navigation satellite systems (GNSS). Among all GNSS, the US GPS (global positioning system) is the most popular. GNSS systems provide absolute positioning based on the information gathered at the GNSS receiver from the GNSS satellite constellation. Because of this, GNSS is subject to relevant problems such as lack of satellite visibility, multipath problems due to the reflection of the satellite signals on surfaces around the receiver’s antenna, jamming, or spoofing [1]. For this reason, it is recommended that the positioning system features some other sensors that, together with the GNSS, provide an overall better performance. The most common configuration is the GNSS, plus the odometry of the vehicle and inertial sensors for attitude determination (a gyro). The values of travelled distance and the heading provided by the odometry and the gyro respectively, work together to provide a dead reckoning (DR) position that supports the GNSS in case of no coverage, and add redundant values to improve the reliability of the whole system [2]. The extra cost of this sensor set is relatively low, as vehicles have already embedded odometry and gyroscopes.

The main concept of DR is that the estimation of the vehicle position is based on the previous one, as spatial increments are calculated from the sensor values. Consequently, the necessary integration process leads to drifts when no absolute updates are obtained. Odometry errors may be due to mechanical or electrical (quantization) issues; tire wear, which changes the wheel diameter over time; and slippages and slides. Among these, the latter is the one that accounts for larger errors in the provision of instant positioning. However, GNSS/DR fusion algorithms do not usually account for slide errors. Therefore, when it happens, the solution is not only more inaccurate, but also inconsistent, since the errors considered by the algorithm are underestimated. This may lead to the malfunction of applications that are based on the confidence of the position solution. For instance, in lane-level applications, the confidence on the system on being on a specific lane at a given instant is crucial: the knowledge of the goodness of the position is as important as the position itself to decide whether a certain action must be taken. This is the concept of position integrity [3].

This article presents a multiple-model particle filter (MMPF) based solution that features two different models running in parallel, one that accounts for slides errors, and another one that does not, choosing at any time which model represents better the vehicle behavior. The simple concept behind this approach lays on the fact that particles will follow different behaviors depending on their assumed model and probability density function, and only those that are a better match with the vehicle motion will remain strong (with relevant weights), serving as the germ for new offspring particles.

The rest of the paper is organized as follows. Section 2 analyzes the most relevant related works. Later, the model for the slide error is introduced in Section 3. Section 4 and Section 5 present the formulations of both the MMPF implementation and the consistency checks, respectively. Section 6 shows and discusses the results. Finally, Section 7 concludes the paper.

2. Related Work Materials and Methods

The literature of the field has a good number of articles featuring GNSS/DR solutions [2,4,5,6,7,8]. Despite the fact that some other technologies may be used to support the estimates along the longitudinal axis of the vehicle, such as accelerometers [4], the use of the odometry is the most widely spread approach [1]. With respect to the estimates of the heading, some authors employ electronic compasses, but many others discard them for lack of consistency and poor performance [9]. To compensate for the errors in the estimates of travelled distance, some authors use visual odometry, like in [10,11]. An interesting approach based on stereo vision for navigation in natural environments can be found in [12]. The robotics community is also quite active in this field, like the work presented in [13] based on cellular automata.

Regarding positioning filters, the most popular solution for fusing GNSS and DR is the extended Kalman filter (EKF), which is a variation of the Kalman filter for non-linear systems [14]. Its success is based on the relative good performance at a low computational cost and simplicity [14]. However, the nature of the vehicle motion is clearly non-linear, and in these cases, some other approaches provide better performances [15]. In these conditions, particle filters (PF), as genetic-type Monte Carlo (MC) methods, use weighted samples to generate approximations of the probability density function. This flexibility (when compared to Kalman), serves well to solve the positioning filtering problem [16,17].

On another note, multiple model (MM) filters have been used with success before by the first author of this article in the problem of positioning error estimation. In [13,18], different interactive multiple model versions of the extended Kalman filter (IMM-EKF) showed good performance for either improving the positioning solution, or maneuver prediction, respectively.

Multiple model particle filters have been applied in the field of tracking of ground, 3D targets and [19,20,21,22,23]. However, there are not many articles with MMPF applied to road vehicle position. The authors of [24] used it for detection and estimation of multipath effects on GPS measurements.

3. Error Model of the Odometry

As it has been aforementioned, odometry suffers from different kind of errors. The one introduced by tire wear has a very low frequency and may be compensated by calibration of the step value. It may be represented as a calibration error with the form ω(k)δr, where ω(k) is the angular rate of the wheels at instant k and δr the difference between the real wheel radius, and the nominal value r.

Errors due to mechanical and electrical noises can be grouped together in a common term with a Gaussian characteristic and zero mean, n(k)~N(0, σ_odo). We have tuned the value of σ_odo to 0.26 m, corresponding with the odometry step in our vehicle setup.

A wheel slide appears when the wheel rotates slower than the value calculated according to the current vehicle speed. Wheel slip is the opposite case, when the wheels rotate faster than they would do in normal friction conditions.

Although both effects may partially compensate one another in a long term, the estimation of the vehicle pose at a given time suffers from slips and slides. In addition, slides appear more often than slips in car navigation. This is the reason why we focus on slides in this paper. Nevertheless, analogous considerations apply for slippages.

The characterization of the odometry error may be completed now to represent slides in the sensor model

$${\epsilon }_{dt}^{slide}\left(k\right)={\delta }^{slide}\left(k\right)+\omega \left(k\right)\delta r+n\left(k\right)$$

(1)

where δ^slide(k) ≥ 0 stands for the sliding error, that may be also developed as

$${\delta }^{slide}\left(k\right)=(1-scv)\times c\left(k\right)$$

(2)

being c(k)~N(0, σ_odo), and scv (slide compensation value) varying from 0 (maximum compensation) till 1 (minimum).

4. Multiple Model Particle Filter Based Method

The principle of the particle filter is to represent by means of a set of N samples {Xⁱ(k)}^N_{i=1} and their corresponding weights {wⁱ(k)}^N_{i=1} the probability density function p(X(k)/Y_{1:k}) at instant k of the state vector X(k), given past observations, following the expression

$$p\left(\mathit{X}\left(k\right)/Y_{1:k}\right)\simeq {\displaystyle \sum _{i=1}^N}{X}^i\left(k\right)\cdot w^i\left(k\right)$$

(3)

where Y_{1:k} stands for the observations collected from the initialization till instant k. Each sample Xⁱ(k) can be described as a Dirac delta expression δⁱ(k)(X(k)) in the form

$${\delta }^i\left(k\right)\left(\mathit{X}\left(k\right)\right)=0if\mathit{X}\left(k\right)\ne X^i\left(k\right)$$

(4)

$${\delta }^i\left(k\right)\left(\mathit{X}\left(k\right)\right)=1if\mathit{X}\left(k\right)=X^i\left(k\right)$$

(5)

The process of particle filtering can be summarized as follows:

• Initialization: Generation of N particles, or samples of the state vector, Xⁱ(0), with equal weights 1/N. The proposed state vector is $\left[x\left(k\right)y\left(k\right)\psi \left(k\right)\right]$, representing east, north and heading (from north to east) at the center of the rear axle of the vehicle.
• Prediction: Estimation of Xⁱ(k + 1) following the prediction model. We use a classical 2D kinematical model for a vehicle on a plane. The measurements of the odometry and the gyroscope work as inputs to the filter. The travelled distance measured by the odometer, ds(k), is estimated when a gyroscope value, $\dot{\psi }\left(k\right)$, is processed. The equation for pose prediction is:

  $$\begin{gathered} x\left(k+1\right)=x\left(k\right)+ds\left(k\right)\sin \mathrm{c}(\dot{\psi }/2)\cos (\psi \left(k\right)+\dot{\psi }\left(k\right)T/2)-\dot{\psi }\left(k\right)T\left(Dx\sin \psi \left(k\right)+Dy\cos \psi \left(k\right)\right) \\ y\left(k+1\right)=y\left(k\right)+ds\left(k\right)\sin \mathrm{c}(\dot{\psi }/2)\sin \left(\psi \left(k\right)+\omega \left(k\right)T/2\right)-\dot{\psi }\left(k\right)T\left(Dx\cos \psi \left(k\right)-Dy\sin \psi \left(k\right)\right) \\ \psi \left(k+1\right)=\psi \left(k\right)+\dot{\psi }\left(k\right)T \end{gathered}$$

  (6)

  being T the sampling period, Dx, Dy the coordinate of the GPS antenna in the body frame, and sinc the cardinal sinus.
• Measurement update: Update of the weights of the particles with the observations Y(k). In our case, the observation vector is $[x_{GPS},y_{GPS}]$, standing for east and north values coming from the GPS. The update is done following the expression

  $$w^i\left(k\right)=w^i\left(k-1\right)\times e^{\left\{-0.5{\left(Y\left(k\right)-h{X}^i\left(k\right)\right)}^{\prime }{R}^{-1}\left(Y\left(k\right)-h{X}^i\left(k\right)\right)\right\}}$$

  (7)

  where h(Xⁱ(k)) is the observation function that relates at instant k the state Xⁱ(k) and observations Y(k) (in our case, simply the second order identity matrix), and R the covariance matrix of observations.
• Normalization of the weights: $w^i\left(k\right)=w^i\left(k\right)/{\sum }_{i=1}^N{w}^i\left(k\right)$.
• Resampling: To prevent high concentration of probability mass in only a few particles, (leading to the convergence of a single wⁱ(k) to 1), particles are resampled if

  $$\frac{1}{{\sum }_{i=1}^N{w}^i{\left(k\right)}^2}<0.5N$$

  (8)
• End of cycle: Making k = k + 1, and iterating to step 2.

In our approach, a fixed number of particles is assigned to the each model.

The addition of the weights of the particles of each model after the observation will indicate the probability that each model m represents properly the vehicle behavior, µ^m(k). This probability is

$${\mu }^m\left(k\right)=\frac{{\sum }_i^{Nm}w{\left(k\right)}_i^m}{{\sum }_i^{Nm}w{\left(k\right)}_i^m+{\sum }_i^{Nm}w{\left(k\right)}_i^{\ne m}}$$

(9)

where w(k)_i^m stands for the weight at instant k of the particle i that represents model m, Nm is the number of particles of each model, that will be equal for all of them, and $w{\left(k\right)}_i^{\ne m}$ stands for the weight at instant k of a particle i that is not driven by model m.

Our solution is based on two different models, named the normal condition model (NCM) and the slide condition model (SCM). Both models will actually share the state vector and prediction equation, but will have different assumptions for the odometry model with and without slides, as described in (1).

Finally, the selected output will be such of the model with higher cumulative weight (more probable). A weighted mixed output from both models, as the one used in [9], would be also possible, but it was found unsuitable for the problem under consideration, as will be shown later in the tests.

5. Filter Consistency

As important as the filter itself, is the capability to evaluate whether or not it performs well. In order to check the performance consistency of the filter under consideration, several methods have been considered, detailed next. Later on the paper, in the sections dedicated to results, the goodness of the proposal will be evaluated based on these methods.

5.1. Filter Covariance

The estimation of the covariance of the filter state at instant k is denoted as matrix $P^m\left(k\right)$, where m stands for the choice of odometry model. Its value can be used to compute the positioning reliability and can be calculated by

$$P^m\left(k\right)=w{\left(k\right)}_i^m\times \left(x{\left(k\right)}_i^m-\overline{x}{\left(k\right)}^m\right)\times \left(x{\left(k\right)}_i^m-\overline{x}{\left(k\right)}^m\right)$$

(10)

where $\overline{x}{\left(k\right)}^m$ is the weighted mean value at instant k of the N particles i that belong to model m, calculated as

$$\overline{x}{\left(k\right)}^m=w{\left(k\right)}_i^m\times x{\left(k\right)}_i^{m}i=1\cdots N$$

(11)

For a quick check, one can plot ellipsis of reliability around a certain position estimate based on its covariance and compare them to the errors to realize whether the errors envelopes are consistent.

5.2. Time Average Autocorrelation

The time average autocorrelation test is based on the ergodicity of the innovation sequence. If the number of time samples, K, is enough, this statistic is normally distributed and its variance is $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$K$}\right.$. Its calculation for innovations one step apart can be done using

$$\overline{\rho }\left(1\right)={\sum }_{k=1}^K{\upsilon \left(k\right)}^{\prime }\upsilon \left(k+1\right)\times {\left[{\displaystyle \sum _{k=1}^K}{\upsilon \left(k\right)}^{\prime }\upsilon \left(k\right)\times {\displaystyle \sum _{k=1}^K}{\upsilon \left(k+1\right)}^{\prime }\upsilon \left(k+1\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(12)

where $\upsilon \left(k\right)$ stands for the innovation at instant k, that can be estimated as the difference between the predicted position and the observation.

This test can be executed in real time, and therefore, in single-run trials [14].

5.3. Time Average Normalized Innovation Square

The value of NIS at instant k can be calculated as

$${ϵ}_{\nu }\left(k\right)={\mathsf{\nu }\left(\mathrm{k}\right)}^{\prime }S{\left(k\right)}^{-1}\mathsf{\nu }\left(\mathrm{k}\right)$$

(13)

being $S\left(k\right)$ the innovation covariance matrix, that can be calculated with

$$S\left(k\right)=H{P}_i\left(k\right)H+R$$

(14)

where R is the matrix of observation covariance, H is the matrix that relates the state vector space with the observation vector space, being in our case

$$H=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right]$$

(15)

and $P_i\left(k\right)$ the estimated covariance of the particle filter at instant k, that can be obtained as

$$P_i\left(k\right)=w{\left(k\right)}_j^i\times \left(x{\left(k\right)}_j^i-\overline{x}{\left(k\right)}^i\right)\times \left(x{\left(k\right)}_j^i–\overline{x}{\left(k\right)}^i\right)$$

(16)

where $\overline{x}{\left(k\right)}^i$ is the weighted mean value at instant k of the N particles j that belong to model i, calculated as

$$\overline{x}{\left(\mathrm{k}\right)}^{\mathrm{i}}=\mathrm{w}{\left(\mathrm{k}\right)}_{\mathrm{j}}^{\mathrm{i}}\times \mathrm{x}{\left(\mathrm{k}\right)}_{\mathrm{j}}^{\mathrm{i}}\mathrm{j}=1\dots \mathrm{N}$$

(17)

The time-average normalized innovation squared can be calculated as

$${\overline{ϵ}}_{\nu }=\frac{1}{K}{\displaystyle \sum _{k=1}^K}{ϵ}_{\nu }\left(k\right)$$

(18)

If the innovation is white, zero mean, and $S\left(k\right)$ represents its covariance, then $K{\overline{ϵ}}_{\nu }$ follows a ${\chi }^2$ distribution.

6. Tests

6.1. Test Setup

The sensor setup included:

• EGNOS capable GPS receiver by Trimble, L1.
• Dual-frequency RTK receiver by Ashtech, for ground reference.
• FOG (Fiber Optic Gyroscope) by KVH.
• Vehicle odometer with 26.15 cm resolution coupled to the rear wheels axle.

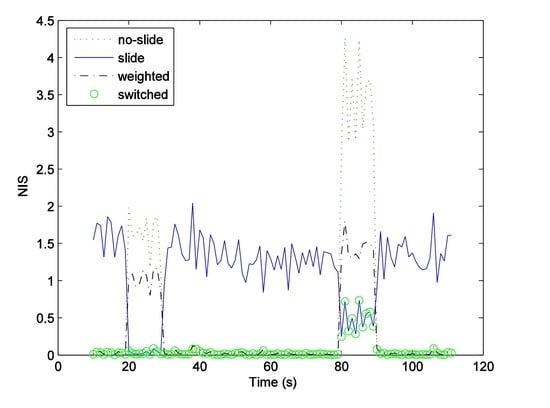
6.2. Results and Discussion

For proving the validity of our proposal, we collected measurements of several acceleration and deceleration conditions, more prone to sliding errors in the odometry along the longitudinal axis. The main objective of the tests is to analyze the capability of the filter to represent the vehicle motion at any time, for what we will use the filter consistency techniques introduced in previous sections. Since both Kalman and particle filters using single models show very similar results, only the results of the particle filter will be discussed.

Figure 1 shows the distribution of particles around the solution in an experiment where the vehicle drives from north to south. Cyan particles are estimated by the SCM while green ones are calculated by the NCM. Even though both solutions are within the possible confidence scenarios, both of them are not the same good. While in the upper cloud, the GPS-EGNOS value matches better the solution that assumes normal conditions, after the slide, the satellite solution fits better the filter output that assumed slides.

Figure 2 shows how model probabilities change at those instants, precisely during the slides. The MMPF manages to identify the sliding situations, and switches to the SCM model, returning to the NCM only when the slide has disappeared. For the same test,

Table 1. Time average correlation results for NCMPF, SCMPF, and MMPF

Model	Value
NCMPF	0.5762
SCMPF	0.9110
MMPF	0.0140

provides the consistency results for all model combinations by using the time average correlation. Low values represent better consistency. For a properly tuned filter, the variance should be ${\sigma }^2=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$K$}\right.$. In our experiment, $\sigma =0.0083$, and the 95% probability region results (−0.01633, 0.01633). Both NCM and SCM fall out of this threshold, only satisfied by the MMPF.

Similar conclusions can be achieved by using the time average NIS indicator (Figure 3). Even if the MMPF encounters some trouble to model the slide around instant 85, it is still the best solution. Additionally, switching models based on each model probability appears to be sounder than a weighted solution.

7. Conclusions

The article focused on the problem of inaccurate positioning and error estimation when GNSS/DR positioning is subject to slides. To do so, the positioning system features two different models, one that accounts for the wheel slides (SCM), and one that does not (NCM). Each model is driven by a particle filter, thus allowing for a more flexible PDF (when compared to the most common extended Kalman filter). The system is capable of switching between both SCM and NCM by means of a multiple model implementation.

Different consistency checks for the filters under consideration are run, showing the goodness of the MMPF with real datasets when compared to the single model implementations. The final positioning system is able to characterize better the errors at any time. On the one hand, particles with stronger weights will survive, and only these are used in the resampling stage. On the other hand, the model whose errors better represent the innovation of the positioning loop is selected.