Deep Embedment (DE) FRP Shear Strengthening of Concrete Bridge Slabs under Loads Close to Supports
Abstract
:1. Introduction
2. Background of Shear Behaviour of Concrete Bridge Deck Slabs
3. Experimental Programme
3.1. Details of Test Slabs
- Influence of strengthening materials, including steel, BFRP (Basalt Fiber Reinforced Polymer), GFRP (Glass Fiber Reinforced Polymer), and CFRP (test specimens labelled as S-S-2-10, S-B-2-9, S-G-2-9, and S-C-2-9);
- Influence of quantity of strengthening embedment bars (test specimens labelled as S-C-2-9 and S-C-1-9). The strengthening configuration is shown in Figure 2c,d;
- Influence of diameter of embedment bars (test specimens labelled as S-C-2-9 and S-C-1-13).
3.2. Strengthening Technique
3.3. Test Set-Up and Monitoring System
3.4. Test Procedure
4. Discussion of Test Results
4.1. Failure Mode and Ultimate Loads
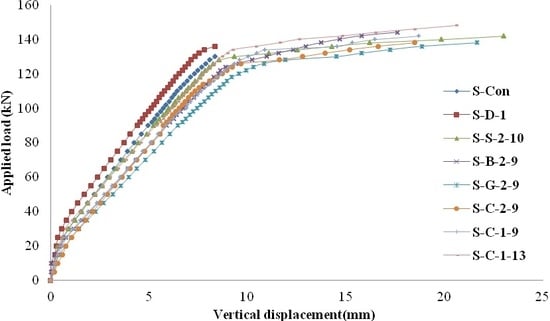
4.2. Load vs. Deflection Responses
4.3. Strain Response
5. Finite Element Analysis
5.1. Proposed NLFEA Model
5.2. Modelling of Concrete Material
5.3. Modelling of Steel and FRP Bars
5.4. Modelling of FRP Bar–to-Concrete Interface
5.5. Solution Strategy
5.6. FE Model Validation
6. Loading-Carrying Capacity Prediction Method
7. Conclusions
- Due to the loading location close to the support, shear failure occurred in the unstrengthened test slabs. The failure mode is brittle and sudden. The deep embedment shear strengthening technique can be used to avoid the occurrence of shear failure of concrete slabs subjected to load close to supports. It was found that the failure mode of concrete slabs varied from brittle shear failure to ductile flexural failure. This was attributed to the broken continuity of shear cracking development by the deep embedment strengthening method.
- It was found that the material type of embedment strengthening materials does not influence the behaviour of strengthened test slabs. Interestingly, increasing the diameter of embedded FRP bars results in larger ultimate capacity and higher ductility.
- Due to the small flexural stiffness of test slabs, the ultimate capacity was enhanced by around 10% by using the deep embedment strengthening method. However, the ductility of the test slabs was improved significantly. The maximum vertical deflection of concrete slabs at failure was increased by more than 100%, and the ductility was increased by more than 200%.
- A NLFEA model for the concrete slabs shear strengthened with deep embedment FRP bars was developed and validated using the test results in this study. This NLFEA model shows a good capability of simulating the structural behaviour of the test slabs accurately, including the ultimate capacity, strain response, and cracking patterns. This numerical model can be used by engineers and researchers for the structural analysis and assessment of the structural performance of concrete slabs strengthened with deep embedment FRP bars.
- By using the model by Modifi et al. [20] to predict the shear resistance contributed by deep embedment FRP bars, a two-way design approach was proposed in this study, in which flexural and shear capacity were predicted separately. With the comparison of the test results, it was found that this theoretical model can predict the loading-carrying capacity and failure mode of the strengthened concrete slabs accurately.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Francisco, N.; Miguel, F.R.; Aurelio, M. Shear strength of RC slabs under concentrated loads near clamped linear support. Eng. Struct. 2014, 76, 10–23. [Google Scholar]
- Rombach, G.A.; Latte, S. Shear resistance of bridge decks without shear reinforcement. In Tailor Made Concrete Structures; Walraven, J.C., Stoelhorst, D., Eds.; Taylor & Francis Group: London, UK, 2008. [Google Scholar]
- Rombach, G.; Kohl, M. Shear design of RC bridge Deck slabs according to Eurocode 2. J. Bridg. Eng. 2013, 18, 1261–1269. [Google Scholar] [CrossRef]
- Teng, J.G.; Chen, J.F.; Smith, S.T.; Lam, L. Behaviour and strength of FRP-strengthened RC structures: A state-of-the-art review. Proc. ICE—Struct. Build. 2003, 156, 51–62. [Google Scholar] [CrossRef]
- Lorenzis, D.L.; Teng, J.G. Near-surface mounted FRP reinforcement: An emerging technique for strengthening structures. Compos. Part B Eng. 2007, 38, 119–143. [Google Scholar] [CrossRef]
- Valerio, P.; Ibell, T.J.; Darby, A.P. Deep embedment of FRP for concrete shear strengthening. Proc. Inst. Civ. Eng. Struct. Build. 2009, 162, 311–321. [Google Scholar] [CrossRef]
- Chaallal, O.; Mofidi, A.; Benmokrane, B.; Neale, K. Embedded through-section FRP rod method for shear strengthening of RC beams: Rerformance and comparison with existing techniques. J. Compos. Constr. ASCE 2011, 15, 374–383. [Google Scholar] [CrossRef]
- Valerio, P.; Ibell, T.; Darby, A. Shear assessment and strengthening of contiguous-beam concrete bridges using FRP bars. In Proceedings of the 7th International Symposium on Fiber Reinforced Polymer Reinforcement for Concrete Structures (FRPRCS-7), Kansas City, MO, USA, 6–9 November 2005; pp. 825–848. [Google Scholar]
- Jemaa, Y.; Jones, C.; Dirar, S. Deep embedment strengthening of full-scale shear deficient reinforced concrete beams. In Proceedings of the 12th International Symposium on Fiber Reinforced Polymers for Reinforced Concrete Structures (FRPRCS-12), Nanjing, China, 14–16 December 2015. [Google Scholar]
- Barros, J.A.O.; Dalfré, G.M.; Trombini, E.; Aprile, A. Exploring the possibilities of a new technique for the shear strengthening of RC elements. In Proceedings of the International Conference of Challenges Civil Construction (CCC2008), Porto, Portugal, 16–18 April 2008. [Google Scholar]
- Rodrigues, V.R. Shear Strength of Reinforced Concrete Bridge Deck Slabs. Ph.D. Thesis, Ecole Polytechnique F′ed′erale de Lausanne, Lausanne, Switzerland, 2007. [Google Scholar]
- McComb, C.; Tehrani, F.M. Enhancement of shear transfer in composite deck with mechanical fasteners. Eng. Struct. 2014, 76, 10–23. [Google Scholar] [CrossRef]
- Lantsoght, E.; Veen, C.V.; Walraven, J. Shear tests of reinforced concrete slabs with concentrated load near to supports. In Proceedings of the 8th fib-PhD Symposium, Kongens Lyngby, Denmark, 20–23 June 2010; pp. 81–86. [Google Scholar]
- Breveglieri, M.; Aprile, A.; Barros, J.A.O. Embedded Through-Section shear strengthening technique using steel and CFRP bars in RC beams of different percentage of existing stirrups. Compos. Struct. 2015, 126, 101–113. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Li, C.H.; Yang, J.B.; Sun, C. Influence of arching action on shear behaviour of laterally restrained concrete slabs reinforced with GFRP bars. Compos. Struct. 2015, 132, 20–34. [Google Scholar] [CrossRef]
- American Concrete Institute (ACI). Guide for the Design and Construction of Concrete Reinforced with FRP Bars; ACI 440.1R-06; ACI: Farmington Hills, MI, USA, 2006. [Google Scholar]
- Mohamed, S.I.; Ibrahim, M.M.; Sherif, M.E. Influence of fibers on flexural behavior and ductility of concrete beams reinforced with GFRP rebars. Eng. Struct. 2011, 33, 1754–1763. [Google Scholar]
- American Association of State Highway and Transportation Officials (AASHTO). Standard Specifications for Design of Highway Bridges; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2000. [Google Scholar]
- HKS (Hibbitt, Karlsson & Sorensen, Inc.). ABAQUS Theory Documentation Version 6.10; HKS: Providence, RI, USA, 2010. [Google Scholar]
- Mofidi, A.; Chaallal, O.; Benmokrane, B.; Neale, K. Experimental tests and design model for RC beams strengthened in shear using the embedded through-section FRP Method. J. Compos. Constr. ASCE 2012, 16, 540–550. [Google Scholar] [CrossRef]
- Michael, Q.; Samir, D.; Yaser, J. Finite element parametric study of reinforced concrete beams shear-strengthened with embedded FRP bars. Compos. Struct. 2016, 149, 93–105. [Google Scholar]
- Lubliner, J.; Oliver, J.S.; Oñate, O.E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–329. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1988, 124, 892–900. [Google Scholar] [CrossRef]
- Zheng, Y.; Robinson, D.; Taylor, S.; Cleland, D. Finite element investigation of structural behaviours of deck slabs in composite bridges. Eng. Struct. 2009, 31, 1762–1776. [Google Scholar] [CrossRef]
- Thorenfeldt, E.; Tomaszemicz, A.; Jensen, J.J. Mechanical properties of high-strength concrete application in design. In Proceedings of the Symposium Utilization of High Strength Concrete, Tapir Trondheim, Norway; 1978; pp. 149–159. [Google Scholar]
- Mattock, A.H.; Kriz, L.B.; Hognestad, E. Rectangular concrete stress distribution in ultimate strength design. Proc. ACI 1961, 57, 875–928. [Google Scholar]
- Hordijk, D.A. Local Approach to Fatigue of Concrete. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1991. [Google Scholar]
- Jendele, L.; Cervenka, J. Finite element modelling of reinforcement with bond. Comput. Struct. 2006, 84, 1780–1791. [Google Scholar] [CrossRef]
- Chen, G.M.; Teng, J.G.; Chen, J.F. Finite-Element modeling of intermediate crack debonding in FRP-plated RC beams. J. Compos. Constr. ASCE 2011, 15, 339–353. [Google Scholar] [CrossRef]
- CEB-FIP. CEB-FIP Model Code 90; Thomas Telford: London, UK, 1993. [Google Scholar]
- Sinha, B.P.; Gerstle, K.H.; Tulin, L.G. Stress-strain relations for concrete under cyclic loading. J. ACI 1964, 61, 195–211. [Google Scholar]
- Reineck, K.H. Hintergründe zur Querkraftbemessung in DIN 1045-1 für Bauteile aus Konstruktionsbeton mit Querkraftbewehrung. Bauingenieur 2001, 76, 168–179. [Google Scholar]
- Zheng, Y.; Robinson, D.; Taylor, S.E.; Cleland, D. Non-linear finite-element analysis of punching capacities of steel–concrete bridge deck slabs. Proc. Inst. Civ. Eng. Struct. Build. 2012, 165, 255–269. [Google Scholar] [CrossRef]
- Ricardo, E.A.; Martha, L.F.; Bitttenourt, T.N. Combination of smeared and discrete approaches with the use of interface elements. In Proceedings of the European Congress on Computational Methods in Applied Sciences and Engineering, Barcelona, Spain, 11–14 September 2000. [Google Scholar]
- BSI. BS 5400: Part 4: British Standard for the Design of Steel, Concrete and Composite Bridges; BSI: London, UK, 1990. [Google Scholar]
- Cosenza, E.; Manfredi, G.; Realfonzo, R. Behaviour and modeling of bond of FRP rebars to concrete. J. Compos. Constr. ASCE 1997, 1, 40–51. [Google Scholar] [CrossRef]

























| Model | Reinforcement Percentage (%) | fcu (MPa) * | Embedment Bar Type | Embedment Strengthening Configuration | Diameter of Embedment Bar/Hole (mm) | Failure Load (kN) | Failure Mode ** | Maximum Deflection at Failure (mm) |
|---|---|---|---|---|---|---|---|---|
| S-Con | 1.1 | 24.5 | N/A | N/A | N/A | 130 | SF | 8.67 |
| S-D-1 | 1.1 | 27 | N/A | N/A | -/16 | 134 | SF | 8.34 |
| S-S-2-10 | 1.1 | 24.5 | Steel | 2 × 2 | 10/16 | 142 | BF | 22.54 |
| S-B-2-9 | 1.1 | 25.1 | BFRP | 2 × 2 | 9/16 | 144 | BF | 17.61 |
| S-G-2-9 | 1.1 | 25.6 | GFRP | 2 × 2 | 9/16 | 140 | BF | 19.36 |
| S-C-2-9 | 1.1 | 25.3 | CFRP | 2 × 2 | 9/16 | 142 | BF | 17.4 |
| S-C-1-9 | 1.1 | 25.4 | CFRP | 2 × 1 | 9/16 | 142 | BF + SF | 18.7 |
| S-C-1-13 | 1.1 | 25.8 | CFRP | 2 × 1 | 13/20 | 148 | BF | 20.58 |
| Deep Embedment Bar/Epoxy | Diameter (mm) | Tensile Strength (MPa) | Elastic Modulus (GPa) | Ultimate Strain |
|---|---|---|---|---|
| Steel | 10 | 504 | 200 | 0.0025 |
| CFRP | 9 | 1581 | 156 | 0.0101 |
| BFRP | 9 | 1011 | 83 | 0.0122 |
| GFRP | 9 | 835 | 480 | 0.0174 |
| FY-Z epoxy | N/A | 40.5 | 1.2 | 0.0017 |
| Model | RP * (%) | fcu (MPa) | EBT ** | ESC *** | Diameter of Embedment Bar/Hole (mm) | DF | Increase in DF Compared to S-Con Beam (%) |
|---|---|---|---|---|---|---|---|
| S-Con | 1.1 | 24.5 | N/A | N/A | N/A | 7.7 | N/A |
| S-D-1 | 1.1 | 27 | N/A | N/A | -/16 | 6.54 | −15% |
| S-S-2-10 | 1.1 | 24.5 | Steel | 2 × 2 | 10/16 | 28.67 | 272% |
| S-B-2-9 | 1.1 | 25.1 | BFRP | 2 × 2 | 9/16 | 23.03 | 199% |
| S-G-2-9 | 1.1 | 25.6 | GFRP | 2 × 2 | 9/16 | 23.05 | 199% |
| S-C-2-9 | 1.1 | 25.3 | CFRP | 2 × 2 | 9/16 | 25.01 | 225% |
| S-C-1-9 | 1.1 | 25.4 | CFRP | 2 × 1 | 9/16 | 20.79 | 170% |
| S-C-1-13 | 1.1 | 25.8 | CFRP | 2 × 1 | 13/20 | 25.44 | 230% |
| Type of FRP | τm (MPa) | sm (mm) | α | p |
|---|---|---|---|---|
| BFRP | 7.42 | 0.13 | 0.085 | 0.0935 |
| GFRP | 7.75 | 0.13 | 0.098 | 0.05 |
| CFRP | 7.69 | 0.11 | 0.087 | 0.068 |
| Test Specimen | Pt-Test * (kN) | Pp-NLFEA ** (kN) | Pp/Pt-NlFEA |
|---|---|---|---|
| S-Con | 130 | 133.06 | 1.02 |
| S-S-2-10 | 142 | 144.28 | 1.02 |
| S-B-2-9 | 144 | 141.84 | 0.98 |
| S-G-2-9 | 138 | 140.71 | 1.02 |
| S-C-2-9 | 138 | 144.78 | 1.05 |
| S-C-1-9 | 142 | 142.93 | 1.00 |
| S-C-1-13 | 148 | 143.92 | 0.97 |
| Average = | 1.01 | ||
| Standard deviation = | 0.03 | ||
| Coefficient of variation = | 0.03 | ||
| Test Specimen | Pt (kN) | Pcs (kN) | PFPRs (kN) | Ps (kN) | Pb (kN) | Pp * (kN) | Pp */Pt |
|---|---|---|---|---|---|---|---|
| S-Con | 130 | 120.4 | — | 120.4 | 137.41 | 120.4 | 0.93 |
| S-B-2-9 | 144 | 120.4 | 15.87 | 136.27 | 137.41 | 136.27 | 0.95 |
| S-G-2-9 | 138 | 120.4 | 14.65 | 135.05 | 137.41 | 135.05 | 0.98 |
| S-C-2-9 | 138 | 120.4 | 35.4 | 155.8 | 137.41 | 137.41 | 1.00 |
| S-C-1-9 | 142 | 120.4 | 38.62 | 159.02 | 137.41 | 137.41 | 0.97 |
| S-C-1-13 | 148 | 120.4 | 62.94 | 183.34 | 137.41 | 137.41 | 0.93 |
| Average = | 0.96 | ||||||
| Standard deviation = | 0.03 | ||||||
| Coefficient of variation = | 0.03 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, L.; Zheng, Y. Deep Embedment (DE) FRP Shear Strengthening of Concrete Bridge Slabs under Loads Close to Supports. Appl. Sci. 2018, 8, 721. https://doi.org/10.3390/app8050721
Xia L, Zheng Y. Deep Embedment (DE) FRP Shear Strengthening of Concrete Bridge Slabs under Loads Close to Supports. Applied Sciences. 2018; 8(5):721. https://doi.org/10.3390/app8050721
Chicago/Turabian StyleXia, Lipeng, and Yu Zheng. 2018. "Deep Embedment (DE) FRP Shear Strengthening of Concrete Bridge Slabs under Loads Close to Supports" Applied Sciences 8, no. 5: 721. https://doi.org/10.3390/app8050721
APA StyleXia, L., & Zheng, Y. (2018). Deep Embedment (DE) FRP Shear Strengthening of Concrete Bridge Slabs under Loads Close to Supports. Applied Sciences, 8(5), 721. https://doi.org/10.3390/app8050721