Optimal Configuration and Path Planning for UAV Swarms Using a Novel Localization Approach
Abstract
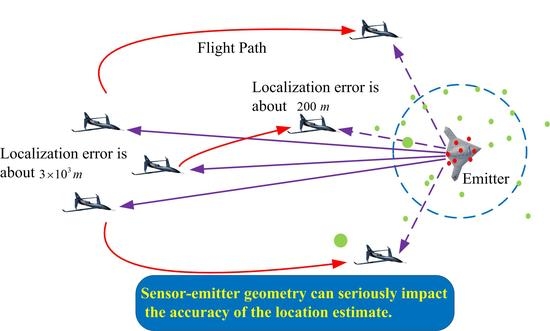
:1. Introduction
2. Problem Formulation
2.1. Measurement Model
2.2. Measurement Variance Model with Distance-Dependent Noise
3. Optimal Configuration Analysis
3.1. Static Emitter Scenario
3.2. Movable Emitter Scenario
- (1)
- Predict:
- (2)
- Update:
4. UAV Path Optimization
5. Simulation Results
5.1. Angle Rule
5.2. Combination of Angle Rule and Distance Rule
5.3. Effect of the Number of UAVs on TDOA Localization Performance
5.4. Dynamic Emitter
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jin, Y.; Liu, X.; Hu, Z.; Li, S. DOA estimation of moving sound sources in the context of nonuniform spatial noise using acoustic vector sensor. Multidimens. Syst. Signal Process. 2015, 26, 321–336. [Google Scholar] [CrossRef]
- Compagnoni, M.; Canclini, A.; Bestagini, P. Source localization and denoising: A perspective from the TDOA space. Multidimens. Syst. Signal Process. 2016, 1–26. [Google Scholar] [CrossRef]
- Chang, S.; Li, Y.; He, Y.; Wang, H. Target Localization in Underwater Acoustic Sensor Networks Using RSS Measurements. Appl. Sci. 2018, 8, 225. [Google Scholar] [CrossRef]
- Domingo-Perez, F.; Lazaro-Galilea, J.L.; Wieser, A. Sensor placement determination for range-difference positioning using evolutionary multi-objective optimization. Exp. Syst. Appl. 2016, 47, 95–105. [Google Scholar] [CrossRef]
- Malanowski, M. Two Methods for Target Localization in Multistatic Passive Radar. IEEE Trans. Aerosp. Electr. Syst. 2012, 48, 572–580. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K.C. A Simple and Efficient Estimator for Hyperbolic Location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Zou, Y.; Liu, H.; Xie, W.; Wan, Q. Semidefinite Programming Methods for Alleviating Sensor Position Error in TDOA Localization. IEEE Access 2017, 5, 23111–23120. [Google Scholar] [CrossRef]
- Yang, B. Different Sensor Placement Strategies for TDOA Based Localization. In Proceedings of the ICASSP, Honolulu, HI, USA, 15–20 April 2007; pp. 1093–1096. [Google Scholar]
- Lui, K.W.K.; So, H.C. A Study of Two-Dimensional Sensor Placement Using Time-Difference-of-Arrival Measurements. Dig. Signal Process. 2009, 19, 650–659. [Google Scholar] [CrossRef]
- Meng, W.; Xie, L.; Xiao, W. Optimality Analysis of Sensor-Source Geometries in Heterogeneous Sensor Networks. IEEE Trans. Wirel. Commun. 2013, 12, 1958–1967. [Google Scholar] [CrossRef]
- Meng, W.; Xie, L.; Xiao, W. Optimal TDOA Sensor-Pair Placement With Uncertainty in Source Location. IEEE Trans. Veh. Technol. 2016, 65, 9260–9271. [Google Scholar] [CrossRef]
- Kim, S.-H.; Park, J.H.; Yoon, W.; Ra, W.-S. A note on sensor arrangement for long-distance target localization. Signal Process. 2017, 133, 18–31. [Google Scholar] [CrossRef]
- Fang, X.; Yan, W.; Zhang, F. Optimal Sensor Placement for Range-Based Dynamic Random Localization. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2393–2397. [Google Scholar] [CrossRef]
- Herath, S.C.K.; Pathirana, P.N. Optimal Sensor Arrangements in Angle of Arrival (AoA) and Range Based Localization with Linear Sensor Arrays. Sensors 2013, 13, 12277–12294. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarunic, P.; Evans, R. Hierarchical Model Predictive Control of UAVs Performing Multitarget-Multisensor Tracking. IEEE Trans. Aeros. Electr. Syst. 2014, 50, 2253–2268. [Google Scholar] [CrossRef]
- Tripathi, A.; Saxena, N.; Mishra, K.K. A nature inspired hybrid optimisation algorithm for dynamic environment with real parameter encoding. Int. J. Bio-Inspir. Comput. 2017, 10, 24–32. [Google Scholar] [CrossRef]
- Dogancay, K. UAV Path Planning for Passive Emitter Localization. IEEE Trans. Aerosp. Electr. Syst. 2012, 48, 1150–1166. [Google Scholar] [CrossRef]
- Frew, E.; Dixon, C.; Argrow, B. Radio source localization by a cooperating UAV team. In Proceedings of the AIAA Infotech@Aerospace, Arlington, TX, USA, 26–29 September 2005. [Google Scholar]
- Wang, X.; Ristic, B.; Himed, B.; Moran, B. Joint Passive Sensor Scheduling for Target Tracking. In Proceedings of the 20th International Conference on Information Fusion, Xi’an, China, 10–13 July 2017; pp. 1671–1677. [Google Scholar]
- Alomari, A.; Phillips, W.; Aslam, N.; comeau, F. Dynamic Fuzzy-Logic Based Path Planning for Mobility-Assisted Localization in Wireless Sensor Networks. Sensors 2017, 17, 1904. [Google Scholar] [CrossRef] [PubMed]
- Kaune, R. Finding Sensor Trajectories for TDOA Based Localization—Preliminary Considerations. In Proceedings of the Workshop Sensor Data Fusion: Trends, Solutions, Applications, Bonn, Germany, 4–6 September 2012. [Google Scholar]
- Kaune, R.; Charlish, A. Online Optimization of Sensor Trajectories for Localization using TDOA Measurements. In Proceedings of the International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 484–491. [Google Scholar]
- Li, X.; Deng, Z.D.; Rauchenstein, L.T.; Carlson, T.J. Contributed Review: Source-localization algorithms and applications using time of arrival and time difference of arrival measurements. Rev. Sci. Instrum. 2016, 87, 041502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaune, R.; Horst, J.; Koch, W. Accuracy Analysis for TDOA Localization in Sensor Networks. In Proceedings of the 14th International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011; pp. 1647–1654. [Google Scholar]
- Huang, B.; Xie, L.; Yang, Z. TDOA-based Source Localization with Distance-dependent Noises. IEEE Trans. Wirel. Commun. 2015, 14, 468–480. [Google Scholar] [CrossRef]
- So, H.C.; Chan, Y.T.; Chan, F.K.W. Closed-form formulae for time-difference-of-arrival estimation. IEEE Trans. Signal Process. 2008, 56, 2614–2620. [Google Scholar] [CrossRef]
- Yan, W.; Fang, X.; Li, J. Formation Optimization for AUV Localization with Range-Dependent Measurements Noise. IEEE Commun. Lett. 2014, 18, 1579–1582. [Google Scholar] [CrossRef]
- Fanaei, M.; Valenti, M.C.; Schmid, N.A.; Alkhweldi, M.M. Distributed parameter estimation in wireless sensor networks using fused local observations. In Proceedings of the SPIE Defense, Security, and Sensing, Baltimore, MD, USA, 9 May 2012; p. 17. [Google Scholar]
- Bar-Shalom, Y.; Li, X.; Kirubarajan, T. Estimation with Applications to Track and Navigation; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Duan, K.; Wang, Z.; Xie, W. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar. IET Signal Process. 2017, 11, 544–553. [Google Scholar] [CrossRef]
- Yahya, N.M.; Tokhi, M.O. A modified bats echolocation-based algorithm for solving constrained optimisation problems. Int. J. Bio-Inspir. Comput. 2017, 10, 12–23. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Koukouvelas, I.; Argyropoulos, N.; Megalooikonomou, V. Quarry monitoring using GPS measurements and UAV photogrammetry. In Proceedings of the SPIE Remote Sensing, Toulouse, France, 10 October 2015; p. 8. [Google Scholar]
- Lai, Y.-C.; Ting, W.O. Design and Implementation of an Optimal Energy Control System for Fixed-Wing Unmanned Aerial Vehicles. Appl. Sci. 2016, 6, 369. [Google Scholar] [CrossRef]
- Rajput, U.; Kumari, M. Mobile robot path planning with modified ant colony optimisation. Int. J. Bio-Inspir. Comput. 2017, 9, 106–113. [Google Scholar] [CrossRef]
- Xu, D.; Xiao, R. An improved genetic clustering algorithm for the multi-depot vehicle routing problem. Int. J. Wirel. Mob. Comput. 2015, 9, 1–7. [Google Scholar] [CrossRef]







| Parameters | Symbols | Values |
|---|---|---|
| Initial emitter position | ||
| Fixed flight velocity | ||
| Sampling time interval | ||
| Signal to noise ratio | ||
| Control vector | ||
| Maximum distance from the UAV platform to the emitter | ||
| Minimum distance from the UAV platform to the emitter | ||
| Safe distance between the UAV platform | ||
| Communication maximum distance | ||
| Barrier parameter for interior point optimization |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Bai, P.; Li, H.; Liang, X. Optimal Configuration and Path Planning for UAV Swarms Using a Novel Localization Approach. Appl. Sci. 2018, 8, 1001. https://doi.org/10.3390/app8061001
Wang W, Bai P, Li H, Liang X. Optimal Configuration and Path Planning for UAV Swarms Using a Novel Localization Approach. Applied Sciences. 2018; 8(6):1001. https://doi.org/10.3390/app8061001
Chicago/Turabian StyleWang, Weijia, Peng Bai, Hao Li, and Xiaolong Liang. 2018. "Optimal Configuration and Path Planning for UAV Swarms Using a Novel Localization Approach" Applied Sciences 8, no. 6: 1001. https://doi.org/10.3390/app8061001
APA StyleWang, W., Bai, P., Li, H., & Liang, X. (2018). Optimal Configuration and Path Planning for UAV Swarms Using a Novel Localization Approach. Applied Sciences, 8(6), 1001. https://doi.org/10.3390/app8061001