SVPWM Method for Multilevel Indirect Matrix Converter with Eliminate Common Mode Voltage
Abstract
:1. Introduction
2. Multilevel Indirect Matrix Converter and the Proposed SVPWM Method
2.1. The Multilevel IMC Topology
2.2. The SVPWM Method for Elimination the CMV
2.2.1. Rectifier Stage Control
2.2.2. Inverter Stage Control
2.3. Maximum Voltage Transfer Ratio
2.4. Switching Sequence
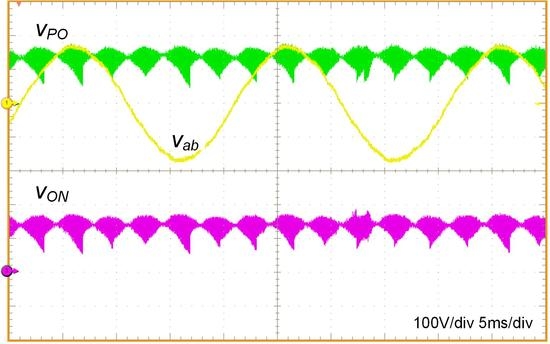
3. Simulation Results and Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wheeler, P.; Rodriguez, J.; Clare, J.; Empringham, L.; Weinstein, A. Matrix converters: A technology review. IEEE Trans. Ind. Electron. 2002, 49, 276–288. [Google Scholar] [CrossRef]
- Kolar, J.W.; Friedli, T.; Rodriguez, J.; Wheeler, P.W. Review of Three-Phase PWM AC–AC Converter Topologies. IEEE Trans. Ind. Electron. 2011, 58, 4988–5006. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Lee, H.-H. Modulation Strategies to Reduce Common-Mode Voltage for Indirect Matrix Converters. IEEE Trans. Ind. Electron. 2012, 59, 129–140. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, X.; Guo, Y.; Deng, W. Speed-sensorless direct torque control scheme for matrix converter driven induction motor. J. Eng. 2018, 2018, 432–437. [Google Scholar] [CrossRef]
- Riedemann, J.; Andrade, I.; Peña, R.; Blasco-Gimenez, R.; Clare, J.; Melín, P.; Rivera, M. Modulation strategies for an open-end winding induction machine fed by a two-output indirect matrix converter. Math. Comput. Simul. 2016, 130, 95–111. [Google Scholar] [CrossRef] [Green Version]
- Arevalo, S.L.; Zanchetta, P.; Wheeler, P.W.; Trentin, A.; Empringham, L. Control and Implementation of a Matrix-Converter-Based AC Ground Power-Supply Unit for Aircraft Servicing. IEEE Trans. Ind. Electron. 2010, 57, 2076–2084. [Google Scholar] [CrossRef]
- Barakati, M.; Kazerani, M.; Aplevich, J. Maximum Power Tracking Control for a Wind Turbine System Including a Matrix Converter. IEEE Trans. Convers. 2009, 24, 705–713. [Google Scholar] [CrossRef]
- Wei, L.; Lipo, T.A. A novel matrix converter topology with simple commutation. In Proceedings of the Thirty-Sixth IAS Annual Meeting, Conference Record of the 2001 IEEE Industry Applications Conference, Chicago, IL, USA, 30 September–4 October 2001; Volume 3, pp. 1749–1754. [Google Scholar]
- Shi, Y.; Yang, X.; He, Q.; Wang, Z. Research on a Novel Capacitor Clamped Multilevel Matrix Converter. IEEE Trans. Electron. 2005, 20, 1055–1065. [Google Scholar] [CrossRef]
- Rmili, L.; Hamouda, M.; Rahmani, S.; Al-Haddad, K. Advanced topologies of multilevel matrix converter. In Proceedings of the 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2015; pp. 599–604. [Google Scholar]
- Lee, M.Y.; Wheeler, P.; Klumpner, C. Space-Vector Modulated Multilevel Matrix Converter. IEEE Trans. Ind. Electron. 2010, 57, 3385–3394. [Google Scholar] [CrossRef]
- Loh, P.C.; Blaabjerg, F.; Gao, F.; Baby, A.; Tan, D.A.C. Pulsewidth Modulation of Neutral-Point-Clamped Indirect Matrix Converter. IEEE Trans. Ind. Appl. 2008, 44, 1805–1814. [Google Scholar] [CrossRef]
- Sun, Y.; Xiong, W.; Su, M.; Li, X.; Dan, H.; Yang, J. Topology and Modulation for a New Multilevel Diode-Clamped Matrix Converter. IEEE Trans. Electron. 2014, 29, 6352–6360. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Lee, H.-H. A New SVM Method for an Indirect Matrix Converter With Common-Mode Voltage Reduction. IEEE Trans. Ind. Informat. 2014, 10, 61–72. [Google Scholar] [CrossRef]
- Padhee, V.; Sahoo, A.; Ned, M. Modulation Techniques for Enhanced Reduction in Common Mode Voltage and Output Voltage Distortion in Indirect Matrix Converters. IEEE Trans. Electron. 2017, 32, 1. [Google Scholar] [CrossRef]
- Rahman, K.; Al-Emadi, N.; Iqbal, A.; Rahman, S. Common mode voltage reduction technique in a three-to-three phase indirect matrix converter. IET Electr. Appl. 2018, 12, 254–263. [Google Scholar] [CrossRef]
- Cha, H.J.; Enjeti, P.N. An approach to reduce common mode voltage in matrix converter. IAS-02 2003, 1, 432–437. [Google Scholar]
- Guan, Q.; Wheeler, P.; Yang, P. Common-mode Voltage Reduction for Matrix Converters Using All Valid Switch States. IEEE Trans. Electron. 2016, 31, 1. [Google Scholar] [CrossRef]
- Nguyen, H.; Lee, H. A Modulation Scheme for Matrix Converters With Perfect Zero Common-Mode Voltage. IEEE Trans. Power Electron. 2016, 31, 5411–5422. [Google Scholar] [CrossRef]
- Nguyen, H.-N.; Lee, H.-H.; Huu-Nhan, N. A DSVM Method for Matrix Converters To Suppress Common-mode Voltage with Reduced Switching Losses. IEEE Trans. Electron. 2016, 31, 1. [Google Scholar] [CrossRef]
- Wang, F.; Wallace, A.; Dai, S.; Von Jouanne, A.; Zhang, H. Multilevel inverter modulation schemes to eliminate common-mode voltages. IEEE Trans. Ind. Appl. 2000, 36, 1645–1653. [Google Scholar] [CrossRef]
- Cailhol, S.; Vidal, P.; Rotella, F. A Generic Method of Pulse width Modulation Applied to Three-Phase Three-Level T-Type NPC Inverter. IEEE Trans. Ind. Appl. 2018, 54, 4515–4522. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, W.W.; Xie, N.; Wang, C.M. Diode-Free T-Type Three-Level Neutral-Point-Clamped Inverter for Low-Voltage Renewable Energy System. IEEE Trans. Ind. Electron. 2014, 61, 6168–6174. [Google Scholar] [CrossRef]



















| Switching State | DC-Link Voltage | ||||||
|---|---|---|---|---|---|---|---|
| Sap1 | Sbp1 | Scp1 | San1 | Sbn1 | Scn1 | VPO | VON |
| Sap2 | Sbp2 | Scp2 | San2 | Sbn2 | Scn2 | ||
| 1 | 0 | 0 | 0 | 1 | 0 | vab | vab |
| 1 | 0 | 0 | 0 | 0 | 1 | vac | vac |
| 0 | 1 | 0 | 0 | 0 | 1 | vbc | vbc |
| 0 | 1 | 0 | 1 | 0 | 0 | vba | vba |
| 0 | 0 | 1 | 1 | 0 | 0 | vca | vca |
| 0 | 0 | 1 | 0 | 1 | 0 | vcb | vcb |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| Inverter Stage’s State | Switching State of Power Switches X = (A, B, C) | Output-Phase Voltage VXO X = (A, B, C) | |||
|---|---|---|---|---|---|
| SX1 | SX2 | SX3 | SX4 | ||
| 1 | 1 | 1 | 0 | 0 | VPO |
| 0 | 0 | 1 | 1 | 0 | 0 |
| −1 | 0 | 0 | 1 | 1 | −VON |
| Input Voltage Phase ωint | Sector | ON Switch | Modulated Switches | Duty Ratios | Instantaneous Split DC-Link Voltages | Average DC-Link Voltage vPN |
|---|---|---|---|---|---|---|
| Upper Rectifier | (dx, dy) | VPO | ||||
| Lower Rectifier | (dx, dy) | VON | ||||
| −π/6 π/6 | I | Sap1 | (Sbn1, Scn1) | (−vb/va, −vc/va) | vab vac | |
| Sap2 | (Sbn2, Scn2) | |||||
| π/6 π/2 | II | Scn1 | (Sbp1, Sap1) | (−vb/vc, −va/vc) | vbc vac | |
| Scn2 | (Sbp2, Sap2) | |||||
| π/2.5π/6 | III | Sbp1 | (Scn1, San1) | (−vc/vb, −va/vb) | vbc vba | |
| Sbp2 | (Scn2, San2) | |||||
| 5π/6.7π/6 | IV | San1 | (Scp1, Sbp1) | (−vc/va, −vb/va) | vca vba | |
| San2 | (Scp2, Sbp2) | |||||
| 7π/6.9π/6 | V | Scp1 | (San1, Sbn1) | (−vb/vc, −vb/va) | vcb vca | |
| Scp2 | (San2, Sbn2) | |||||
| 9π/6.11π/6 | VI | Sbn1 | (Scp1, Sap1) | (−vc/vb, −va/vb) | vab vcb | |
| Sbn2 | (Scp2, Sap2) | (-vc/vb, −va/vb) | ||||
| Space Vectors | Switching States | Type of Vector | Vector Magnitude | ||
|---|---|---|---|---|---|
| (−1,−1,−1) | 0 | 0 | Zero vector | 0 | |
| (0,0,0) | 0 | 0 | |||
| (1,1,1) | 0 | 0 | |||
| (1,0,0) | 0 | Small vector | |||
| (0,−1,−1) | 0 | ||||
| (1,1,0) | |||||
| (0,0,−1) | |||||
| (0,1,0) | |||||
| (−1,0,−1) | |||||
| (0,1,1) | 0 | ||||
| (−1,0,0) | 0 | ||||
| (0,0,1) | |||||
| (−1,−1,0) | |||||
| (1,0,1) | |||||
| (0,−1,0) | |||||
| (1,0,−1) | Medium Vector | ||||
| (0,1,−1) | 0 | ||||
| (−1,1,0) | |||||
| (−1,0,1) | |||||
| (0,−1,1) | 0 | ||||
| (1,−1,0) | |||||
| (1,−1,−1) | 0 | Large vector | |||
| (1,1,−1) | |||||
| (−1,1,−1) | |||||
| (−1,1,1) | 0 | ||||
| (−1,−1,1) | |||||
| (1,−1,1) |
| Inverter Stage’s Switching State | Common Mode Voltage |
|---|---|
| (0,0,0) | 0 |
| (−1,−1,−1) | −VDC/2 |
| (1,1,1) | VDC/2 |
| (1,0,0); (0,1,0); (0,0,1); (−1,1,1); (1,−1,1); (1,1,−1) | VDC/6 |
| (0,0,−1); (−1,0,0); (0,−1,0); (1,−1,−1); (−1,1,−1); (−1,−1,1) | −VDC/6 |
| (1,0,−1); (0,1,−1); (−1,1,0); (−1,0,1); (0,−1,1); (1,−1,0) | 0 |
| (1,1,0); (1,0,1); (0,1,1) | VDC/3 |
| (0,−1,−1); (−1,0,−1); (−1,−1,0) | −VDC/3 |
| Input voltage (Vin) | 100 V |
| Input frequency (fin) | 50 Hz |
| R load | 20 Ω |
| L load | 20 mH |
| Output frequency (fout) | 40 Hz |
| Sampling period (Ts) | 100 kHz |
| Voltage transfer ratio (m) | 1.2 |
| Voltage Transfer Ratio (m) | THD of Input Current (%) | THD of Output Voltage |
|---|---|---|
| 0.2 | 0.42 | 6.48 |
| 0.4 | 1.52 | 4.57 |
| 0.6 | 2.62 | 3.48 |
| 0.8 | 3.80 | 2.76 |
| 1.0 | 4.55 | 2.30 |
| 1.2 | 6.20 | 1.94 |
| 1.4 | 6.82 | 1.60 |
| Model Name | Manufacturer | Rated Voltage | Rated Current | Power Switches in Figure 3 |
|---|---|---|---|---|
| SK 60GM123 | Semikron | 1200 V | 50 A | Sap1, San1, Sbp1, Sbn1, Scp1,Scn1 Sap2, San2, Sbp2, Sbn2, Scp2,Scn2 SA2, SA3, SB2, SB3, SC2, SC3 |
| FMG 2G 50US60 | Fairchild Semiconductor | 600 V | 50 A | SA1, SA4, SB1, SB4, SC1, SC4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dinh Tuyen, N.; Minh Phuong, L. SVPWM Method for Multilevel Indirect Matrix Converter with Eliminate Common Mode Voltage. Appl. Sci. 2019, 9, 1342. https://doi.org/10.3390/app9071342
Dinh Tuyen N, Minh Phuong L. SVPWM Method for Multilevel Indirect Matrix Converter with Eliminate Common Mode Voltage. Applied Sciences. 2019; 9(7):1342. https://doi.org/10.3390/app9071342
Chicago/Turabian StyleDinh Tuyen, Nguyen, and Le Minh Phuong. 2019. "SVPWM Method for Multilevel Indirect Matrix Converter with Eliminate Common Mode Voltage" Applied Sciences 9, no. 7: 1342. https://doi.org/10.3390/app9071342
APA StyleDinh Tuyen, N., & Minh Phuong, L. (2019). SVPWM Method for Multilevel Indirect Matrix Converter with Eliminate Common Mode Voltage. Applied Sciences, 9(7), 1342. https://doi.org/10.3390/app9071342