Impact of Permeable Membrane on the Hydrocyclone Separation Performance for Oily Water Treatment
Abstract
:1. Introduction
2. Methodology
2.1. Problem Description
2.2. Computational Domain Generation
2.3. Mathematical Modeling
- Incompressible and Newtonian fluid with constant physical–chemical properties;
- Steady-state and isothermal flow;
- Mass transfer, interfacial momentum, and mass source are disregarded;
- The non-drag interfacial forces (lift forces, wall lubrication, virtual mass, turbulent dispersion and solid pressure) were neglected;
- Constant drag coefficient equal to 0.44, due to the established turbulent flow;
- The geometry walls are static and there is null wall roughness.
- The water stream is a multicomponent mixture of water and oil (solute);
- The composition of the multicomponent water/oil mixture is variable;
- The viscosity and density of the mixture are constant;
- The mass diffusion coefficient of the oil in the water is constant;
- The porous medium (ceramic membrane) has constant permeability and isotropic distribution of it pores;
- The pore obstruction by the solute was neglected (constant porosity);
- The concentration polarization layer is present and its thickness is considered uniform and homogeneous, thus the resistance resulting from the presence of this layer was defined at the fluid–membrane interface (concentration polarization resistance);
- The rate of local permeation is determined by the series resistance theory;
- The non-slip condition on the membrane surface was adopted;
- There is no reaction or adsorption of the solute on the contact surface in the porous medium.
2.3.1. The Governing Equations
- (a)
- Mass Conservation Equation:
- (b)
- Momentum Conservation Equation:
- (c)
- Turbulence Model:
- (d)
- Separation Efficiency:
2.3.2. Boundary Conditions
- (a)
- Input:
- (b)
- Porous Wall (Permeate):
- (c)
- Outputs (Concentrated and Diluted):
- (d)
- Non-porous walls:
2.4. Studied Cases
3. Results and Discussion
3.1. Mesh Quality Assessment
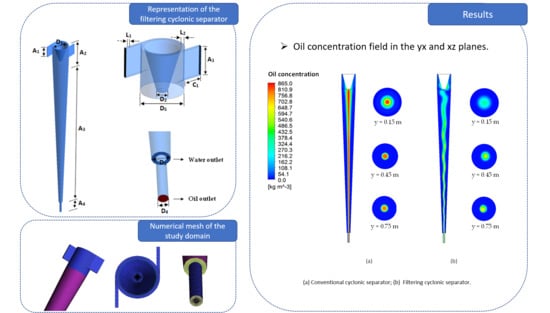
3.2. Comparative Study between the Conventional Cyclonic Separator and the Cyclonic Filter Separator
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vieira, L.G.M. Optimization of Separation Processes in Filtering Hydrocyclones. Ph.D. Thesis, Federal University of Uberlândia, Uberlândia, Brazil, 2006. (In Portuguese). [Google Scholar]
- Farias, F.P.M.; Lima, A.G.B.; Neto, S.R.F. Influence of the cyclone’s lower outlet duct used as a dryer: Modeling and simulation. In Proceedings of the XVII Brazilian Congress of Chemical Engineering, Recife, Brazil, 14–17 September 2008. (In Portuguese). [Google Scholar]
- Farias, F.P.M.; Souza, J.S.; Lima, W.C.P.B.; Mâcedo, A.C.; Neto, S.R.F.; Lima, A.G.B. Influence of Geometric Parameters of the Hydrocyclone and Sand Concentration on the Water/Sand/Heavy-Oil Separation Process: Modeling and Simulation. Int. J. Multiphysics 2011, 5, 187–202. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, E.S. Geometrical and Hydrodynamic Aspects of a Hydrocyclone in the Separation Process of Multiphase Systems: Application to the Oil Industry. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2011. (In Portuguese). [Google Scholar]
- Luna, F.D.T. Numerical Study of the Separation Process of a Two-Phase System in a Cyclonic Separator. Master’s Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2014. (In Portuguese). [Google Scholar]
- Ishak, K.E.H.K.; Ayoub, M.A. Performance of liquid–liquid hydrocyclone (LLHC) for treating produced water from surfactant flooding produced water. World J. Eng. 2019, 17, 215–222. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Hamza, J.E.; Lemmu, T.A. Performance enhancement of axial concurrent liquid–liquid hydrocyclone separator through optimization of the swirler vane angle. J. Pet. Explor. Prod. Technol. 2020, 10, 1957–2967. [Google Scholar] [CrossRef]
- Souza, J.S.; Farias, F.P.M.; Swarnakar, R.; Neto, S.R.F.; Lima, A.G.B. Non-Isothermal Separation Process of Two-Phase Mixture Water/Ultra-Viscous Heavy Oil by Hydrocyclone. Adv. Chem. Eng. Sci. 2011, 1, 271–279. [Google Scholar] [CrossRef] [Green Version]
- Farias, F.P.M.; Souza, J.S.; Lima, W.C.P.B.; Mâcedo, A.C.; Neto, S.R.F.; Lima, A.G.B. The Effect of Droplet Diameter on the Separation of the Heavy-Oil from Water using Hydrocyclone CFD Simulation. In Proceedings of the 3 ed International Conference on Advanced Computational Engineering and Experimenting. ACE-X, Roma, Italy, 22–23 June 2009. [Google Scholar]
- Wang, B.; Yu, A.B. Numerical study of particle-fluid flow in hydrocyclones with different body dimensions. Miner. Eng. 2006, 19, 1022–1033. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, L.; Yang, X.; Wang, Y.; Xu, B.; Liang, B. Innovative Design and Study of an Oil-water Coupling Separation Magnetic Hydrocyclone. Sep. Purif. Technol. 2019, 213, 389–400. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Osei, H.; Hashim, F.M.; Hamza, J.E. Flow structures and their impact on single and dual inlets hydrocyclone performance for oil-water separation. J. Pet. Explor. Prod. Technol. 2019, 9, 2943–2952. [Google Scholar] [CrossRef] [Green Version]
- Damak, K.; Ayadi, A.; Zeghmati, B.; Schmitz, P. Concentration polarisation in tubular membranes-a numerical approach. Desalination 2004, 171, 139–153. [Google Scholar] [CrossRef]
- Souza, J.S. Theoretical Study of the Microfiltration Process in Ceramic Membranes. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2014. (In Portuguese). [Google Scholar]
- Cunha, A.L. Treatment of Effluents from the Oil Industry via Ceramic Membranes-Modeling and Simulation. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2014. (In Portuguese). [Google Scholar]
- Lira, D.S. Process of Microfiltration of Textile Effluents Using OCA Fiber Membrane-Modeling and Simulation. Master’s Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2018. (In Portuguese). [Google Scholar]
- Magalhães, H.L.F.; Moreira, G.; Gomez, R.S.; Porto, T.R.N.; Correia, B.R.B.; Silva, A.M.V.; Neto, S.R.F.; Lima, A.G.B. Non-Isothermal Treatment of Oily Waters Using Ceramic Membrane: A Numerical Investigation. Energies 2020, 13, 92. [Google Scholar] [CrossRef]
- Vieira, L.G.M.; Damasceno, J.J.R.; Barrozo, M.A.S. Improvement of hydrocyclone separation performance by incorporating a conical filtering wall. Chem. Eng. Process. Process Intensif. 2010, 49, 460–467. [Google Scholar] [CrossRef]
- Silva, N.K.G.; Silva, D.O.; Vieira, L.G.M.; Barrozo, M.A.S. Effects of underflow diameter and vortex finder length on the performance of a newly designed filtering hydrocyclone. Powder Technol. 2015, 286, 305–310. [Google Scholar] [CrossRef]
- Salvador, F.F.; Barrozo, M.A.S.; Vieira, L.G.M. Filtering cylindrical-conical hydrocyclone. Particuology 2019, 47, 54–62. [Google Scholar] [CrossRef]
- Façanha, J.M.F.; Silva, D.O.; Barrozo, M.A.S.; Vieira, L.G.M. Analysis of the use of a filtering medium in different parts of a centrifugal separator. Mater. Sci. Forum 2012, 727–728, 20–25. [Google Scholar]
- Roache, P.J. Perspective: A method for uniform Reporting of Grid Refinement studies. ASME J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Karatekin, I.C.O. Numerical Experiments on Application of Richarson Extrapolation with Nonuniform Grids. ASME J. Fluid Eng. 1997, 119, 584–590. [Google Scholar]
- Paudel, S.; Saenger, N. Grid refinement study for three dimensional CFD model involving incompressible free surface flow and rotating object. Comput. Fluids 2017, 143, 134–140. [Google Scholar] [CrossRef]
- Nunes, S.A. Modeling and Simulation of the Produced Water Treatment Using a Filtering Cyclonic Separator. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2019; 170p. (In Portuguese). [Google Scholar]
- Moraes, C.A.C. Fuidodynamic Model for the Estimation of Efficiency in Hydrocyclones for Oily Water. Master’s Thesis, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil, 2004. (In Portuguese). [Google Scholar]
- Cullivan, J.C.; Williams, R.A.; Dyakowski, T.; Cross, C.R. New under-standing of a hydrocyclone flow field and separation mechanism from computational fluid dynamics. Miner. Eng. 2004, 17, 651–660. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Ibrahim, G.A.; Mohamed, G.F. Performance of a three-product hydrocyclone. Chem. Eng. Sci. 2008, 91, 34–40. [Google Scholar] [CrossRef]
- Vieira, T.M.; Souza, J.S.; Barbosa, E.S.; Cunha, A.L.; Neto, S.R.F.; Lima, A.G.B. Numerical study of oil/water separation by ceramic membranes in the presence of turbulent flow. Adv. Chem. Eng. Sci. 2012, 2, 257–265. [Google Scholar]
- He, F.; Wang, H.; Wang, J.; Li, S.; Fan, Y.; Xu, X. Experimental study of mini-hydrocyclones with different vortex finder depths using Particle Imaging Velocimetry. Sep. Purif. Technol. 2020, 236, 1–10. [Google Scholar] [CrossRef]
- Cavalcante, D.C.M. Study of the Fluid Dynamics of the Solid Particle/Water Separation Process via Filtering Hydrocyclone: Modeling and Simulation. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2017. (In Portuguese). [Google Scholar]
- Svarovsky, L. Hidrociclones; Holt, Rinehard & Winston: Esatbourne, UK, 1984; p. 198. [Google Scholar]
- Buriti, C.J.O.; Farias, F.P.M.; Neto, S.R.F.; Lima, A.G.B. Performance and numerical evaluation of the heavy and ultraviscous water/oil separation process inside a hydrocyclone. In Proceedings of the 5º Brazilian Congress of R & D in Petroleum and Gas, Fortaleza, Brazil, 18–22 October 2009. (In Portuguese). [Google Scholar]
- Freitas, A.G.B. Modeling and Simulation of Oily Water Treatment Using Hydrocyclone. Master’s Thesis, Federal University of Sergipe, São Cristovão, Brazil, 2009. (In Portuguese). [Google Scholar]
- Zimmermann, M.S. Lead/Air Separation Process Using Cyclonic Separator: Modeling and Simulation. Master’s Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2018. (In Portuguese). [Google Scholar]
- Salvador, F.F. Experimental Study of the Behavior of a Cone Hydrocyclone and Filter Cylinder. Master’s Thesis, Federal University of Uberlândia, Uberlândia, Brazil, 2013. (In Portuguese). [Google Scholar]
- Mota, A.R.P.; Borges, C.P.; Kiperstok, A.; Esquerre, K.P.; Araujo, P.M.; Branco, L.P.N. Produced water treatment for oil removal by membrane separation process: Review. Eng. Sanit. Ambient. 2013, 18, 15–26. [Google Scholar]












| Tangential Inlets (mm) | Height (A1) | 50 |
| Length (C1) | 50 | |
| Width (L1) | 5 | |
| Upper Conical Part (mm) | Height (A2) | 75 |
| Width (L2) | 5 | |
| Top Diameter (D1) | 65 | |
| Bottom Diameter (D2) | 18 | |
| Cylindrical Section (mm) | Height (A2) | 75 |
| Diameter (D5) | 70 | |
| Conical Section (mm) | Height (A3) | 725 |
| Annular Outlet (mm) | Diameter (D3) | 18 |
| Tubular Outlet (mm) | Diameter (D4) | 10 |
| Height (A4) | 50 |
| Membrane | Permeability | [16] |
| Polarization layer thickness | [16] | |
| Porosity | 0.4 | |
| Water | Density | |
| Viscosity | ||
| Molar mass | ||
| Oil | Density | |
| Viscosity | ||
| Molar mass | ||
| The average oil drop diameter |
| Case | Input Velocity (m/s) | Oil Volumetric Fraction (%) | Membrane Rejection Index R (-) |
|---|---|---|---|
| 01 | 5 | 5.0 | - |
| 02 | 15 | 7.5 | - |
| 03 | 5 | 5.0 | 1 |
| 04 | 15 | 7.5 | 1 |
| Mesh | Number of Elements | Simulation Time | |
|---|---|---|---|
| Cyclonic Separator | Filtering Separator | ||
| M1 | 337.360 | 1 d 4 h 17′26″ | 3 d 8 h 4′2″ |
| M2 | 71,352 | 3 h 10′44’’ | 21 h 38′40″ |
| M3 | 10,571 | 23′22″ | 17′4″ |
| Separator | Mass Flow Rate (kg/s) | |||||||
|---|---|---|---|---|---|---|---|---|
| Water | Oil | Water | Oil | |||||
| Input | Input | Annular Output | Tubular Outlet | Membrane | Annular Output | Tubular Outlet | ||
| Conventional Cyclonic | 6.91 | 0.48 | 5.19 | 1.72 | - | 2.02 × 10−4 | 0.48 | |
| Filtering Cyclonic | 6.91 | 0.48 | 4.41 | 1.76 | 0.74 | 1.99 × 10−4 | 0.46 | |
| Separator | Total Efficiency (%) | Liquid Ratio (%) | Reduced Efficiency (%) |
|---|---|---|---|
| Conventional Cyclonic | 99.95 | 24.94 | 99.94 |
| Filtering Cyclonic | 96.07 | 25.46 | 94.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunes, S.A.; Magalhães, H.L.F.; de Farias Neto, S.R.; Lima, A.G.B.; Nascimento, L.P.C.; Farias, F.P.M.; Lima, E.S. Impact of Permeable Membrane on the Hydrocyclone Separation Performance for Oily Water Treatment. Membranes 2020, 10, 350. https://doi.org/10.3390/membranes10110350
Nunes SA, Magalhães HLF, de Farias Neto SR, Lima AGB, Nascimento LPC, Farias FPM, Lima ES. Impact of Permeable Membrane on the Hydrocyclone Separation Performance for Oily Water Treatment. Membranes. 2020; 10(11):350. https://doi.org/10.3390/membranes10110350
Chicago/Turabian StyleNunes, Sirlene A., Hortência L. F. Magalhães, Severino R. de Farias Neto, Antonio G. B. Lima, Lucas P. C. Nascimento, Fabiana P. M. Farias, and Elisiane S. Lima. 2020. "Impact of Permeable Membrane on the Hydrocyclone Separation Performance for Oily Water Treatment" Membranes 10, no. 11: 350. https://doi.org/10.3390/membranes10110350
APA StyleNunes, S. A., Magalhães, H. L. F., de Farias Neto, S. R., Lima, A. G. B., Nascimento, L. P. C., Farias, F. P. M., & Lima, E. S. (2020). Impact of Permeable Membrane on the Hydrocyclone Separation Performance for Oily Water Treatment. Membranes, 10(11), 350. https://doi.org/10.3390/membranes10110350