Storm Waves at the Shoreline: When and Where Are Infragravity Waves Important?
Abstract
:1. Introduction
1.1. Background and Literature
1.2. Scope of Research
- Compiling a dataset comprising observations in previously unrecorded combinations of wave and morphological conditions;
- Assessing how swash height in the gravity (Sg) and infragravity bands (Sig) relates to offshore wave height (H0);
- Examining how accurately previous parameterizations of Sig, developed over a limited range of wave and morphological conditions, can be used to predict Sig across the range of morphologies in the new dataset, and whether an improved parameter can be obtained;
- Developing a conceptual model to illustrate the importance of infragravity swash at the shoreline on a wide variety of beach morphologies under a wide range of high-energy swell and wind-wave combinations.
2. Materials and Methods
2.1. Description of Field Sites
2.2. Field Data Collection and Video Data Processing
3. Results
3.1. Enviornmental Conditions
3.2. Comparison of Spectra at Wavebuoy and Shoreline
3.3. Reletionship between Swash and Offshore Wave Height (H0)
3.4. The Role of Wave Height, Period, and Beach Slope
3.4.1. Stockdon (S2006)—Sandy Beaches
3.4.2. Poate—Gravel Beaches
3.4.3. Deepwater Wave Power
3.4.4. Comparison of Parameterizations
4. Discussion
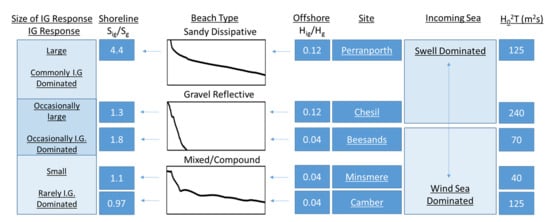
Conceptual Diagram—When and Where Are Infragravity Waves Important at the Shoreline?
5. Summary and Conclusions
- Infragravity waves were observed in the swash at all sites, becoming important when H0 exceeded approximately 1.3 m. For a given wave height, infragravity waves in the swash were enhanced on gravel and sandy beaches, but suppressed on mixed/compound beaches.
- Infragravity waves were observed to become most dominant in the swash on the low sloping sandy beach, where Sig/Sg exceeded 4. They occasionally dominated the gravel beaches, but to a lesser extent (<1.8), and rarely or never dominated the mixed/compound sites (<1.1). This was attributed to differences in short wave dissipation patterns resulting from contrasting morphology and wave steepness.
- A previously published empirical relationship [10], Sig = 0.06 (H0L0)0.5, developed on sandy beaches, predicted Sig well on the sandy beach and the mixed sand and gravel beach, over a comparable range of conditions to those in which it was developed. Stockdon was shown to under-predict Sig for higher-energy conditions and for data collected on gravel beaches, suggesting Sig was enhanced under these conditions.
- A new gravel specific predictor of Sig was proposed, by linearly fitting observations of Sig from two separate field deployments to terms from Poate’s gravel runup equation, (tan β)1/2H0Tp. This was seen to underestimate values of Sig on the sandy beach.
- H02T, proportional to offshore wave power, was a good predictor of Sig at the sites where IG could become dominant, yielding the equation Sig = 0.02(H02T) + 0.42, valid for high-energy conditions.
- The relationship between Sig and H02T across a diverse range of sites implied that, under extreme wave conditions, wave height and period became more important than local morphology as a control on infragravity in the swash. Conversely, at sites where IG rarely dominated, infragravity swash height remained small at the shoreline regardless of offshore conditions. This highlights the importance of collecting data over the unique range of heights and periods present here.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McCall, R.T.; Van Thiel de Vries, J.S.M.; Plant, N.G.; Van Dongeren, A.R.; Roelvink, J.A.; Thompson, D.M.; Reniers, A.J.H.M. Two-dimensional time dependent hurricane overwash and erosion modeling at Santa Rosa Island. Coast. Eng. 2010, 57, 668–683. [Google Scholar] [CrossRef]
- Roelvink, D.; Reniers, A.; van Dongeren, A.; van Thiel de Vries, J.; McCall, R.; Lescinski, J. Modelling storm impacts on beaches, dunes and barrier islands. Coast. Eng. 2009, 56, 1133–1152. [Google Scholar] [CrossRef]
- Russell, P.E. Mechanisms for beach erosion during storms. Cont. Shelf Res. 1993, 13, 1243–1265. [Google Scholar] [CrossRef]
- Raubenheimer, B.; Guza, R.T. Observations and predictions of run-up. J. Geophys. Res. Ocean. 1996, 101, 25575–25587. [Google Scholar] [CrossRef]
- Oltman-shay, J. Infragravity Energy and its Implications in Nearshore Sediment Transport and Sandbar Dynamics; Forgotten Books: London, UK, 1989. [Google Scholar]
- Senechal, N.; Coco, G.; Bryan, K.R.; Holman, R.A. Wave runup during extreme storm conditions. J. Geophys. Res. Ocean. 2011, 116, 1–13. [Google Scholar] [CrossRef]
- Fiedler, J.W.; Brodie, K.L.; McNinch, J.E.; Guza, R.T. Observations of runup and energy flux on a low-slope beach with high-energy, long-period ocean swell. Geophys. Res. Lett. 2015, 42, 9933–9941. [Google Scholar] [CrossRef]
- Inch, K.; Davidson, M.; Masselink, G.; Russell, P. Observations of nearshore infragravity wave dynamics under high energy swell and wind-wave conditions. Cont. Shelf Res. 2017, 138, 19–31. [Google Scholar] [CrossRef]
- Bertin, X.; de Bakker, A.; van Dongeren, A.; Coco, G.; Andrée, G.; Ardhuinf, F.; Bonneton, P.; Bouchette, F.; Castelle, B.; Crawford, W.; et al. Infragravity wave: From driving mechanisms to impacts. Earth Sci. Rev. 2018, 1–70. [Google Scholar] [CrossRef]
- Stockdon, H.F.; Holman, R.A.; Howd, P.A.; Sallenger, A.H. Empirical parameterization of setup, swash, and runup. Coast. Eng. 2006, 53, 573–588. [Google Scholar] [CrossRef]
- Masselink, G.; Puleo, J.A. Swash-zone morphodynamics. Cont. Shelf Res. 2006, 26, 661–680. [Google Scholar] [CrossRef]
- Passarella, M.; Goldstein, E.B.; De Muro, S.; Coco, G. The use of genetic programming to develop a predictor of swash excursion on sandy beaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 599–611. [Google Scholar] [CrossRef]
- Gomes da Silva, P.; Medina, R.; González, M.; Garnier, R. Infragravity swash parameterization on beaches: The role of the profile shape and the morphodynamic beach state. Coast. Eng. 2018, 136, 41–55. [Google Scholar] [CrossRef]
- Guedes, R.M.C.; Bryan, K.R.; Coco, G.; Holman, R.A. The effects of tides on swash statistics on an intermediate beach. J. Geophys. Res. Ocean. 2011, 116, 1–13. [Google Scholar] [CrossRef]
- Guedes, R.M.C.; Bryan, K.R.; Coco, G. Observations of wave energy fluxes and swash motions on a low-sloping, dissipative beach. J. Geophys. Res. Ocean. 2013, 118, 3651–3669. [Google Scholar] [CrossRef]
- Hunt, I.A. Design of Seawalls and Breakwaters. J. Waterw. Harb. Div. 1959, 85, 123–152. [Google Scholar]
- Poate, T.G.; McCall, R.T.; Masselink, G. A new parameterisation for runup on gravel beaches. Coast. Eng. 2016, 117, 176–190. [Google Scholar] [CrossRef]
- Guza, R.T.; Thornton, E.B. Swash oscillations on a natural beach. J. Geophys. Res. 1982, 87, 483–491. [Google Scholar] [CrossRef]
- Ruessink, B.G.; Kleinhans, M.G.; van den Beukel, P.G.L. Observations of swash under highly dissipative conditions. J. Geophys. Res. 1998, 103, 3111–3118. [Google Scholar] [CrossRef]
- Ruggiero, P.; Holman, R.A.; Beach, R.A. Wave run-up on a high-energy dissipative beach. J. Geophys. Res. C Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Jennings, R.; Shulmeister, J. A field based classification scheme for gravel beaches. Mar. Geol. 2002, 186, 211–228. [Google Scholar] [CrossRef]
- Harley, M. Coastal Storm Definition. In Coastal Storms: Processes and Impacts; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 1–21. [Google Scholar]
- Battjes, J.A. Surf Similarity. In Proceedings of the 14th International Conference on Coastal Engineering, Copenhagen, Denmark, 24–28 June 1974; pp. 466–480. [Google Scholar]
- Almeida, L.P.; Masselink, G.; Russell, P.; Davidson, M.; Poate, T.; McCall, R.; Blenkinsopp, C.; Turner, I. Observations of the swash zone on a gravel beach during a storm using a laser-scanner (Lidar). J. Coast. Res. 2013, 65, 636–641. [Google Scholar] [CrossRef]
- Almeida, L.P.; Masselink, G.; Russell, P.E.; Davidson, M.A. Observations of gravel beach dynamics during high energy wave conditions using a laser scanner. Geomorphology 2015, 228, 15–27. [Google Scholar] [CrossRef]
- Earlie, C.S.; Young, A.P.; Masselink, G.; Russell, P.E. Coastal cliff ground motions and response to extreme storm waves. Geophys. Res. Lett. 2015, 847–854. [Google Scholar] [CrossRef]
- Holland, K.T.; Holman, R.A.; Lippmann, T.C.; Stanley, J.; Plant, N. Practical Use of Video Imagery in Nearshore Oceanographic Field Studies. IEEE J. Ocean. Eng. 1997, 22, 81–92. [Google Scholar] [CrossRef]
- Austin, M.J.; Masselink, G. Observations of morphological change and sediment transport on a steep gravel beach. Mar. Geol. 2006, 229, 59–77. [Google Scholar] [CrossRef]
- Scott, T.; Masselink, G.; Russell, P. Morphodynamic characteristics and classi fi cation of beaches in England and Wales. Mar. Geol. 2011, 286, 1–20. [Google Scholar] [CrossRef]
- Burvingt, O.; Masselink, G.; Russell, P.; Scott, T. Classification of beach response to extreme storms. Geomorphology 2017, 295, 722–737. [Google Scholar] [CrossRef]
- Wiggins, M.; Scott, T.; Masselink, G.; Russell, P.; McCarroll, R.J. Coastal embayment rotation: Response to extreme events and climate control, using full embayment surveys. Geomorphology 2019, 327, 385–403. [Google Scholar] [CrossRef]










| Map No | Site/Experiment | Date | H0 (m) | Tp (s) | Tan β | D50 (mm) | ξ0 | N | Sig (m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Duck, NC (USA) Duck82 | 5–25 October 1982 | 0.7–4.1 1.71 | 6.3–16.5 11.9 | 0.09–0.16 0.12 | 0.75 | 0.68–2.38 1.44 | 36 | 0.4–2.4 1.2 |
| 2 | Scripps, CA (USA) | 26–29 June 1989 | 0.5–0.8 0.69 | 10–10 10 | 0.03–0.06 0.04 | 0.20 | 0.4–0.92 0.6 | 41 | 0.3–0.7 0.33 |
| 1 | Duck, NC (USA) Duck90–Delilah | 6–19 October 1990 | 0.5–2.5 1.40 | 4.7–14.8 9.3 | 0.03–0.14 0.09 | 0.36 | 0.44–1.70 0.90 | 138 | 0.4–1.7 0.91 |
| 4 | San Onofre, CA (USA) | 16–20 October 1993 | 0.5–1.1 0.8 | 13–17 14.9 | 0.07–0.13 0.1 | - | 1.6–2.62 2.2 | 59 | 0.5–1.8 0.96 |
| 3 | Gleneden, OR (USA) | 26–28 February 1994 | 1.8–2.2 2.1 | 10.5–16 12.4 | 0.03–0.11 0.08 | - | 0.26–1.2 0.9 | 42 | 0.9–1.9 1.4 |
| 5 | Tersheling (Netherlands) | 2–22 April 1994 1–21 October 1994 | 0.5–3.9 1.9 | 4.8–10.6 8.3 | 0.01–0.03 0.02 | 0.22 | 0.07–0.22 0.1 | 14 | 0.2–0.9 0.54 |
| 1 | Duck, NC (USA) Duck94 | 3–21 October 1994 | 0.7–4.1 1.5 | 3.8–14.8 10.5 | 0.06–0.1 0.08 | 0.20–2.5 | 0.33–1.43 0.81 | 52 | 0.5–2.2 0.81 |
| 6 | Agate, OR (USA) | 11–17 February 1996 | 1.8–3.1 2.5 | 7.1–14.3 11.9 | 0.01–0.02 0.02 | 0.20 | 0.1–0.19 0.15 | 14 | 0.7–1.5 1.1 |
| 1 | Duck, NC (USA) Duck97–SandyDuck | 3–30 October 1997 | 0.4–3.6 1.3 | 3.7–15.4 9.5 | 0.05–0.14 0.09 | 0.90–1.66 | 0.34–3.22 1.1 | 95 | 0.3–1.8 0.88 |
| 7 | Truc Vert (France) | 3 March–13 April 2008 | 1.1–6.4 2.4 | 11.2–16.4 13.7 | 0.05–0.08 0.06 | 0.35 | 0.49–0.9 0.68 | 88 | 0.63–2.37 1.3 |
| 8 | Tairua (New Zealand) | 15–17 July 2008 | 0.7–1.0 - | 9.9–12.5 11.0 | 0.09–0.13 - | 0.4 | 1.4–2.25 - | 25 | 0.6–0.95 0.75 |
| 9 | Ngarunui (New Zealand) | 8–9 November 2010 | 0.6–1.3 - | 8.1–12.4 9.0 | 0.01–0.03 - | 0.29 | 0.13–0.42 - | 32 | 0.24–0.90 0.60 |
| 10 | Somo (Spain) | 4 May 2016 | 0.3–0.7 0.31 | 11.0–13.0 12.0 | 0.04–0.1 0.06 | 0.28–0.35 | 0.9–2.5 1.5 | 12 | 0.28–0.90 0.57 |
| Site | Description | Storm Name Date Return Period (Years) | H0_95 (m) | H0 (m) Range | Tp_95 (s) | Tp (s) Range | ξ0 Typical Range * |
|---|---|---|---|---|---|---|---|
| Perranporth (PPT) | High-energy, dissipative sandy beach, exposed to oceanic swell and locally generated wind waves | Unnamed storm 31 January–7 February 2017 1 in 1 | 3.1 | 1.6–3.2 | 15.4 | 11.1–18.2 | 0.14–0.33 |
| Chesil (CSL) | Medium-energy, reflective gravel beach, partially exposed to oceanic swell and locally generated wind waves | “Petra” 5–6 February 2014 1 in 10 | 2.6 | 1.6–6.6 | 15.3 | 10.3–16.7 | 1.1–5.5 |
| Beesands (BEE) | Low-energy, reflective gravel beach, dominated by wind waves and occasional refracted oceanic swell | “Beast from the east/Emma” 20–27 February 2018 1 in 60 | 1.9 | 0.4–3.3 | 14.3 | 5.1–15.0 | 0.5–2.4 |
| Camber (CAM) | Low-energy, fetch-limited, compound beach with steep gravel upper and low slope sandy terrace | “Angus” 4–6 November 2016 1 in 10 | 2.0 | 0.9–3.8 | 11.1 | 5.5–10.0 | 0.06–1.5 |
| Minsmere (MMR) | Low-energy, fetch-limited, mixed sand and gravel beach. Steep upper shore face, low slope below low water. Submerged offshore bar | Unnamed storm 6–8 January 2018 1 in 5 | 1.9 | 0.52–2.5 | 8.3 | 3.3–7.7 | 0.14–1.5 |
| Site/Experiment | Date | H0 (m) | Tp (s) | Tan β | D50 (mm) | ξ0 | N | Sig (m) |
|---|---|---|---|---|---|---|---|---|
| Beesands, UK | 20–27 February 2018 | 0.4–3.3 2.0 | 5.1–15.0 7.4 | 0.09–0.11 0.10 | - 5 | 0.53–2.84 0.71 | 75 | 0.20–2.3 1.3 |
| Perranporth, UK | 31 January–7 February 2017 | 1.6–3.2 2.4 | 11.1–18.2 15.7 | 0.02–0.08 0.034 | - 0.25 | 0.19–0.96 0.44 | 31 | 1.1–3.6 2.2 |
| Camber Sands, UK | 5–6 November 2016 | 0.9–3.8 2.2 | 5.5–10.0 7.7 | 0.02–0.10 * - | 0.33–10 * - | 0.059–1.1 1 | 16 | 0.30–0.81 0.53 |
| Minsmere, UK | 6–8 January 2018 | 0.52–2.5 1.6 | 3.3–7.7 6.4 | 0.03–0.13 ** - | 0.33–20 ** - | 0.1–0.97 0.21 | 43 | 0.01–0.68 0.33 |
| Chesil, UK | 5–6 February 2014 | 1.6–6.6 3.9 | 10.3–16.7 13.8 | 0.24–0.38 0.32 | 65 - | 2.21–3.84 3.7 | 40 | 0.65–11.4 5.1 |
| Site | Regression Slope (m) | Intercept (c) | R2 | p | RMSE (m) |
|---|---|---|---|---|---|
| CSL | 2.02 | −2.82 | 0.86 | <0.005 | 1.29 |
| PPT | 1.06 | −0.40 | 0.67 | <0.005 | 0.44 |
| BEE | 0.51 | 0.30 | 0.65 | <0.005 | 0.28 |
| MMR | 0.25 | −0.06 | 0.67 | <0.005 | 0.11 |
| CAM | 0.04 | 0.44 | 0.03 | 0.51 | 0.16 |
| Combined | 1.66 | −2.01 | 0.78 | <0.005 | 1.00 |
| Equation | Site | R2 | Bias | p-Value |
|---|---|---|---|---|
| S2006 Sig = 0.06 (H0L0)0.5 | ||||
| Perranporth | 0.61 | −0.33 | <0.005 | |
| Beesands | 0.36 | −0.57 | <0.005 | |
| Minsmere | 0.63 | 0.27 | <0.005 | |
| Camber | 0.12 | 0.32 | 0.014 | |
| Chesil | 0.60 | −3.0 | <0.005 | |
| Equation (5) Sig = 0.15(tan β)0.5H0Tp + 0.43 | ||||
| Perranporth | 0.59 | −0.73 | <0.005 | |
| Beesands | 0.54 | −0.21 | <0.005 | |
| Minsmere | 0.65 | 0.34 | <0.005 | |
| Camber | 0.16 | 0.36 | 0.123 | |
| Chesil | 0.86 | 0.22 | <0.005 | |
| Equation (6) Sig = 0.02(H02T) + 0.42 | ||||
| Perranporth | 0.70 | 0.3 | <0.005 | |
| Beesands | 0.52 | −0.23 | <0.005 | |
| Minsmere | 0.65 | 0.49 | <0.005 | |
| Camber | 0.09 | 0.72 | 0.248 | |
| Chesil | 0.81 | 0.38 | <0.005 |
| Shoreline | Offshore | |||
|---|---|---|---|---|
| Site | Sig (m) | Sig/Sg | Hsig (m) | Hig/Hg |
| PPT | 2.5 | 4.4 | 0.42 | 0.14 |
| CSL | 6.4 | 1.3 | 0.73 | 0.13 |
| BEE | 1.9 | 1.8 | 0.10 | 0.04 |
| MMR | 0.7 | 1.1 | 0.09 | 0.04 |
| CAM | 0.8 | 0.97 | 0.16 | 0.04 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Billson, O.; Russell, P.; Davidson, M. Storm Waves at the Shoreline: When and Where Are Infragravity Waves Important? J. Mar. Sci. Eng. 2019, 7, 139. https://doi.org/10.3390/jmse7050139
Billson O, Russell P, Davidson M. Storm Waves at the Shoreline: When and Where Are Infragravity Waves Important? Journal of Marine Science and Engineering. 2019; 7(5):139. https://doi.org/10.3390/jmse7050139
Chicago/Turabian StyleBillson, Oliver, Paul Russell, and Mark Davidson. 2019. "Storm Waves at the Shoreline: When and Where Are Infragravity Waves Important?" Journal of Marine Science and Engineering 7, no. 5: 139. https://doi.org/10.3390/jmse7050139
APA StyleBillson, O., Russell, P., & Davidson, M. (2019). Storm Waves at the Shoreline: When and Where Are Infragravity Waves Important? Journal of Marine Science and Engineering, 7(5), 139. https://doi.org/10.3390/jmse7050139