Two-Dimensional Tungsten Disulfide-Based Ethylene Glycol Nanofluids: Stability, Thermal Conductivity, and Rheological Properties
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Material Characterization Techniques
2.2.2. Nanofluid Preparation
2.2.3. Nanofluid Measurement Instruments/Techniques
3. Results
3.1. Material Characterization Analysis
3.2. Stability and Particle Size Distribution Analysis
Effect of Surfactants on Stability of WS2/EG Nanofluids
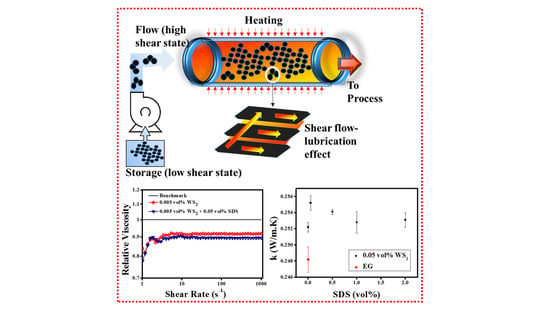
3.3. Thermal Conductivity Analysis
3.4. Rheological Analysis
3.4.1. Oscillation Measurements (Strain Sweep Test)
3.4.2. Rotational Measurements (Shear Flow Behavior)
3.4.3. Temperature Sweep Study
4. Conclusions
- The size and morphology of WS2 NPs was confirmed and found to be well in agreement with the supplier data sheet.
- The addition of SDS (0.05%) increased the zeta potential by ~88% in comparison to 0.005% pristine nanofluid. This rate of improvement reduced to 37% per 0.05% SDS addition when 0.5% SDS was incorporated, but the absolute value of the zeta potential increased. Similarly, for other nanofluid combinations with SDS, the absolute zeta potential values improved, but the rate of improvement with regards to surfactant concentrations became slow as the amount of surfactant increased. In the case of SDS addition, the maximum increment in agglomerate size appeared at ~172%, ~245%, and 261%, corresponding to 0.005% WS2 + 2% SDS, 0.01% WS2 + 2% SDS, and 0.02% WS2 + 0.05% SDS, respectively. Collectively, the zeta potential improved to 554% while the mean particle size also showed an increase up to 411% due to the adsorption of surfactant molecules. This might cause agglomeration with aging, leading to flocculation and sedimentation.
- The maximum thermal conductivity enhancement was observed to be ~ 2.8%, 1.9%, and 4.5% for combinations of 0.05% SDS + 0.005% WS2, corresponding to operating temperatures of 25 °C, 50 °C, and 70 °C, respectively. Subsequently, the increased concentration of SDS decreased the thermal conductivity which is a common observation for higher concentration of surfactants. Like the 0.005% WS2, the higher concentrations such as 0.01% WS2 and 0.02% WS2 also show higher enhancement corresponding to lower surfactant concentrations. However, the elevated temperature behavior showed an oscillating response and the reason may lie within the detachment of surfactant molecules and the interaction with WS2 sheets. Therefore, it needs to be explored further. Collectively, the maximum thermal conductivity of pristine nanofluids increased from 3.5% to 6.9% with the addition of surfactants. However, the results also revealed that the maximum thermal conductivity improvement did not correspond to the high zeta potential. Thus, rigorous concentration optimization is always a decisive parameter for the optimum heat transfer fluid solution.
- The oscillation rheology showed a rational verification of structured network formation inside nanofluids with WS2 NPs and also depicted the nanofluids’ behavior transition from viscous to elastic with surfactants. The viscous to elastic structural transition suggested that a higher initial pumping input was required to initiate the fluid flow.
- The anomalous viscosity reduction of ~8.2% corresponding to the minimum volume concentration (0.005%) of WS2 witnessed the super-fluidity of pristine WS2/EG nanofluids. In addition, the synergistic effect of small volume concentrations (0.05%) of SDS surfactant was also notable with 0.005% WS2, which further reduced the viscosity, and the final reduction became ~10.5%. However, higher concentrations of SDS, SDBS, and CTAB are not beneficial for synergistic effects with nanoparticles, as noted in the present work.
- All the tested samples revealed a non-Newtonian to Newtonian behavior transition at a shear rate of 10 s−1.
- Particularly for 0.05% SDS with 0.005% WS2, thermal conductivity was enhanced by up to 4.5%, with a corresponding decrease in viscosity of up to 10.5%, in a temperature range of 25–70 °C as compared to EG.
- All in all, the thermal conductivity enhancement up to 6.9% and dynamic viscosity up to 10.5% proposed that the WS2/EG nanofluids can be considered as potential candidates for engineering applications. However, WS2 based nanofluids have been characterized here for the first time. Therefore, further experimental evaluation is proposed to develop a database of their stability, thermal conductivity, and rheology for comparison purposes.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khullar, V.; Tyagi, H.; Hordy, N.; Otanicar, T.P.; Hewakuruppu, Y.; Modi, P.; Taylor, R.A. Harvesting solar thermal energy through nanofluid-based volumetric absorption systems. Int. J. Heat Mass Transf. 2014, 77, 377–384. [Google Scholar] [CrossRef]
- Chougule, S.S.; Sahu, S.K. Comparative Study of Cooling Performance of Automobile Radiator Using Al2O3-Water and Carbon Nanotube-Water Nanofluid. J. Nanotechnol. Eng. Med. 2014, 5, 010901. [Google Scholar] [CrossRef]
- Aberoumand, S.; Jafarimoghaddam, A. Tungsten (III) oxide (WO3)—Silver/transformer oil hybrid nanofluid: Preparation, stability, thermal conductivity and dielectric strength. Alex. Eng. J. 2018, 57, 169–174. [Google Scholar] [CrossRef]
- Pal, B.; Mallick, S.S.; Pal, B. Remarkably Improved Dispersion Stability and Thermal Conductivity of WO3–H2O Suspension by SiO2 Coating. J. Nanosci. Nanotechnol. 2018, 18, 3283–3290. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, C.T.; Desgranges, F.; Roy, G.; Galanis, N.; Maré, T.; Boucher, S.; Mintsa, H.A. Temperature and particle-size dependent viscosity data for water-based nanofluids–hysteresis phenomenon. Int. J. Heat Fluid Flow 2007, 28, 1492–1506. [Google Scholar] [CrossRef]
- Karimi-Nazarabad, M.; Goharshadi, E.K.; Youssefi, A. Particle shape effects on some of the transport properties of tungsten oxide nanofluids. J. Mol. Liq. 2016, 223, 828–835. [Google Scholar] [CrossRef]
- Naik, M.T.; Janardhana, G.R.; Reddy, K.V.K.; Reddy, B.S. Experimental investigation into rheological property of copper oxide nanoparticles suspended in propylene glycol–water based fluids. ARPN J. Eng. Appl. Sci. 2010, 5, 29–34. [Google Scholar]
- Karimi-Nazarabad, M.; Goharshadi, E.K.; Entezari, M.H.; Nancarrow, P. Rheological properties of the nanofluids of tungsten oxide nanoparticles in ethylene glycol and glycerol. Microfluid. Nanofluidics 2015, 19, 1191–1202. [Google Scholar] [CrossRef]
- SU, S.C. Enhancing the rmal conductivity of fluids with nanoparticles, developments and applications of non-Newtonian flows. In Proceedings of the 1995 International mechanical engineering congress and exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Namburu, P.K.; Kulkarni, D.P.; Misra, D.; Das, D.K. Viscosity of copper oxide nanoparticles dispersed in ethylene glycol and water mixture. Exp. Therm. Fluid Sci. 2007, 32, 397–402. [Google Scholar] [CrossRef]
- Pastoriza-Gallego, M.J.; Casanova, C.; Legido, J.L.; Piñeiro, M.M. CuO in water nanofluid: Influence of particle size and polydispersity on volumetric behaviour and viscosity. Fluid Phase Equilib. 2011, 300, 188–196. [Google Scholar] [CrossRef]
- Chen, L.; Xie, H.; Li, Y.; Yu, W. Nanofluids containing carbon nanotubes treated by mechanochemical reaction. Thermochim. Acta 2008, 477, 21–24. [Google Scholar] [CrossRef]
- Kedzierski, M.A. Viscosity and density of CuO nanolubricant. Int. J. Refrig. 2012, 35, 1997–2002. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, J.; Grey, F.; Liu, J.Z.; Liu, Y.; Wang, Y.; Yang, Y.; Cheng, Y.; Zheng, Q. Observation of microscale superlubricity in graphite. Phys. Rev. Lett. 2012, 108, 205503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yeo, S.; Nandi, D.K.; Rahul, R.; Kim, T.H.; Shong, B.; Jang, Y.; Bae, J.-S.; Han, J.W.; Kim, S.-H.; Kim, H. Low-temperature direct synthesis of high quality WS2 thin films by plasma-enhanced atomic layer deposition for energy related applications. Appl. Surf. Sci. 2018, 459, 596–605. [Google Scholar] [CrossRef]
- Durairaj, A.; Jennifer, D.L.; Sakthivel, T.; Obadiah, A.; Vasanthkumar, S. Development of tungsten disulfide ZnO nanohybrid photocatalyst for organic pollutants removal. J. Mater. Sci. Mater. Electron. 2018, 29, 19413–19424. [Google Scholar] [CrossRef]
- Rapoport, L.; Bilik, Y.; Feldman, Y.; Homyonfer, M.; Cohen, S.R.; Tenne, R. Hollow nanoparticles of WS2 as potential solid-state lubricants. Nature 1997, 387, 791–793. [Google Scholar] [CrossRef]
- Lee, D.-W.; Tolochko, O.V.; Turaev, F.R.; Kim, D.; Kim, B.-K. Synthesis and characterization of WS2 nanoparticles by chemical vapor condensation. Nanosci. Nanotechnol. 2009, 9, 1–6. [Google Scholar]
- Kamel, M.S.; Lezsovits, F. Experimental Investigation on Pool Boiling Heat Transfer Performance Using Tungsten Oxide WO3 Nanomaterial-Based Water Nanofluid. Materials 2020, 13, 1922. [Google Scholar] [CrossRef]
- Martínez-Merino, P.; Alcántara, R.; Aguilar, T.; Gallardo, J.J.; Carrillo-Berdugo, I.; Gómez-Villarejo, R.; Rodríguez-Fernández, M.; Navas, J. Stability and Thermal Properties Study of Metal Chalcogenide-Based Nanofluids for Concentrating Solar Power. Energies 2019, 12, 4632. [Google Scholar] [CrossRef] [Green Version]
- Zhu, D.; Wang, L.; Yu, W.; Xie, H. Intriguingly high thermal conductivity increment for CuO nanowires contained nanofluids with low viscosity. Sci. Rep. 2018, 8, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Merino, P.; Midgley, S.D.; Martín, E.I.; Estellé, P.; Alcántara, R.; Sánchez-Coronilla, A.; Grau-Crespo, R.; Navas, J. Novel WS2-Based Nanofluids for Concentrating Solar Power: Performance Characterization and Molecular-Level Insights. ACS Appl. Mater. Interfaces 2020, 12, 5793–5804. [Google Scholar] [CrossRef] [PubMed]
- Saterlie, M.S.; Sahin, H.; Kavlicoglu, B.; Liu, Y.; Graeve, O.A. Surfactant effects on dispersion characteristics of copper-based nanofluids: A dynamic light scattering study. Chem. Mater. 2012, 24, 3299–3306. [Google Scholar] [CrossRef]
- Lee, D.; Kim, J.-W.; Kim, B.G. A new parameter to control heat transport in nanofluids: Surface charge state of the particle in suspension. J. Phys. Chem. B 2006, 110, 4323–4328. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, D.; Askari, S.; Patel, J.; Macias-Montero, M.; Mitra, S.; Zhang, R.; Lin, W.F.; Mariotti, D.; Maguire, P. Enhanced Dispersion of TiO2 Nanoparticles in a TiO2/PEDOT:PSS hybrid Nanocomposite via Plasma-Liquid Interactions. Sci. Rep. 2015, 5, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Hu, M.; Jing, D. The synergistic effect between surfactant and nanoparticle on the viscosity of water-based fluids. Chem. Phys. Lett. 2019, 727, 1–5. [Google Scholar] [CrossRef]
- Sharma, P.; Baek, I.; Cho, T.; Park, S.; Lee, K.B.; Bong, K. Enhancement of thermal conductivity of ethylene glycol based silver nano fl uids. Powder Technol. 2011, 208, 7–19. [Google Scholar] [CrossRef]
- Singh, M.; Kundan, L. Experimental Study on Thermal Conductivity and Viscosity of Al2O3-Nanotransformer Oil. Int. J. Theor. Appl. Res. Mech. Eng. 2013, 2, 125–130. [Google Scholar]
- Sani, E.; Vallejo, J.P.; Cabaleiro, D.; Lugo, L. Functionalized graphene nanoplatelet-nanofluids for solar thermal collectors. Sol. Energy Mater. Sol. Cells 2018, 185, 205–209. [Google Scholar] [CrossRef]
- Holman, J.P. Experimental Methods for Engineers, 8th ed.; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Yu, L.; Bian, Y.; Liu, Y.; Xu, X. Experimental investigation on rheological properties of water based nanofluids with low MWCNT concentrations. Int. J. Heat Mass Transf. 2019, 135, 175–185. [Google Scholar] [CrossRef]
- Yarbrough, K.; Pradhan, S.K.; Kogo, G.; Roul, M.; Lin, P.; Zhang, K.; Baumgart, H.; Bahoura, M. Thickness Controlled Nanostructure Formation in RF Sputtered WS2 Thin Film. Mater. Res. Express 2018. [Google Scholar] [CrossRef]
- Mahler, B.; Hoepfner, V.; Liao, K.; Ozin, G.A. Colloidal synthesis of 1T-WS2 and 2H-WS2 nanosheets: Applications for photocatalytic hydrogen evolution. J. Am. Chem. Soc. 2014, 136, 14121–14127. [Google Scholar] [CrossRef] [PubMed]
- Scherrer, P. Zsigmondy’s Kolloidchemie; BoD–Books on Demand: Norderstedt, Germany, 2012. [Google Scholar]
- Vattikuti, S.V.; Byon, C. Effect of CTAB surfactant on textural, structural, and photocatalytic properties of mesoporous WS2. Sci. Adv. Mater. 2015, 7, 2639–2645. [Google Scholar] [CrossRef]
- Liu, L.; Stetsyuk, V.; Kubiak, K.J.; Yap, Y.F.; Chai, J.C. Nanoparticles for convective heat transfer enhancement: Heat transfer coefficient and the effects of particle size and zeta potential. Chem. Eng. Commun. 2018, 206, 761–771. [Google Scholar] [CrossRef] [Green Version]
- Graves, J.E.; Latvytė, E.; Greenwood, A.; Emekwuru, N.G. Ultrasonic preparation, stability and thermal conductivity of a capped copper-methanol nanofluid. Ultrason. Sonochem. 2019, 55, 25–31. [Google Scholar] [CrossRef]
- Seong, H.J.; Kim, G.N.; Jeon, J.H.; Jeong, H.M.; Noh, J.P.; Kim, Y.J.; Kim, H.J.; Huh, S.C. Experimental study on characteristics of grinded graphene nanofluids with surfactants. Materials 2018, 11, 950. [Google Scholar] [CrossRef] [Green Version]
- Umar, S.; Sulaiman, F.; Abdullah, N.; Mohamad, S.N. Investigation of the effect of pH adjustment on the stability of nanofluid. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2018; Volume 2031, p. 020031. [Google Scholar] [CrossRef]
- Carrillo-Berdugo, I.; Zorrilla, D.; Sánchez-Márquez, J.; Aguilar, T.; Gallardo, J.J.; Gómez-Villarejo, R.; Alcántara, R.; Fernández-Lorenzo, C.; Navas, J. Interface-inspired formulation and molecular-level perspectives on heat conduction and energy storage of nanofluids. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Fang, W.; Feng, Y.; Geng, Q.; Song, M. Stability properties of water-based gold and silver nanofluids stabilized by cationic gemini surfactants. J. Taiwan Inst. Chem. Eng. 2019, 458–465. [Google Scholar] [CrossRef]
- Che Sidik, N.A.; Mahmud Jamil, M.; Aziz Japar, W.M.A.; Muhammad Adamu, I. A review on preparation methods, stability and applications of hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 80, 1112–1122. [Google Scholar] [CrossRef]
- Korada, V.S.; Hamid, N.H.B. Engineering Applications of Nanotechnology: From Energy to Drug Delivery; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Ilyas, S.U.; Pendyala, R.; Marneni, N. Settling Characteristics of Alumina Nanoparticles in Ethanol-Water Mixtures. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Schwyz, Switzerland, 2013; Volume 372, pp. 143–148. [Google Scholar] [CrossRef]
- Michael, M.; Zagabathuni, A.; Ghosh, S.; Pabi, S.K. Thermo-physical properties of pure ethylene glycol and water–ethylene glycol mixture-based boron nitride nanofluids: An experimental investigation. J. Therm. Anal. Calorim. 2018, 5, 369–380. [Google Scholar] [CrossRef]
- Xia, G.; Jiang, H.; Liu, R.; Zhai, Y. Effects of surfactant on the stability and thermal conductivity of Al2O3/de-ionized water nanofluids. Int. J. Therm. Sci. 2014, 84, 118–124. [Google Scholar] [CrossRef]
- Ilhan, B.; Kurt, M.; Ertürk, H. Experimental investigation of heat transfer enhancement and viscosity change of hBN nanofluids. Exp. Therm. Fluid Sci. 2016, 77, 272–283. [Google Scholar] [CrossRef]
- Thomas, S.; Sobhan, C.B.; Taha-Tijerina, J.; Narayanan, T.N.; Ajayan, P.M. Investigations on Transient Natural Convection in Boron Nitride-Mineral Oil Nanofluid Systems. In ASME 2012 International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2013; p. 671. [Google Scholar]
- Sarviya, R.M.; Fuskele, V. Review on Thermal Conductivity of Nanofluids. Mater. Today Proc. 2017, 4, 4022–4031. [Google Scholar] [CrossRef]
- Shah, J.; Ranjan, M.; Sooraj, K.P.; Sonvane, Y.; Gupta, S.K. Surfactant prevented growth and enhanced thermophysical properties of CuO nanofluid. J. Mol. Liq. 2019, 283, 550–557. [Google Scholar] [CrossRef]
- Ebrahimi, R.; de Faoite, D.; Finn, D.P.; Stanton, K.T. Accurate measurement of nanofluid thermal conductivity by use of a polysaccharide stabilising agent. Int. J. Heat Mass Transf. 2019, 136, 486–500. [Google Scholar] [CrossRef]
- Selvam, C.; Mohan Lal, D.; Harish, S. Thermal conductivity and specific heat capacity of water–ethylene glycol mixture-based nanofluids with graphene nanoplatelets. J. Therm. Anal. Calorim. 2017, 129, 947–955. [Google Scholar] [CrossRef]
- Leong, K.Y.; Mohd Hanafi, N.; Mohd Sohaimi, R.; Amer, N.H. The effect of surfactant on stability and thermal conductivity of carbon nanotube based nanofluids. Therm. Sci. 2016, 20, 429–436. [Google Scholar] [CrossRef]
- Żyła, G.; Fal, J.; Estellé, P. Thermophysical and dielectric profiles of ethylene glycol based titanium nitride (TiN–EG) nanofluids with various size of particles. Int. J. Heat Mass Transf. 2017, 113, 1189–1199. [Google Scholar] [CrossRef]
- Hermida-Merino, C.; Perez-Rodriguez, M.; Pineiro, M.M.; Pastoriza-Gallego, M.J. Evidence of viscoplastic behavior of exfoliated graphite nanofluid. Soft Matter 2010, 4, 2264–2275. [Google Scholar] [CrossRef]
- Franck, A. Understanding Rheology of Structured Fluids. Available online: http://www.tainstruments.com/pdf/literature/AAN016_V1_U_StructFluids.pdf (accessed on 7 July 2020).
- Beheshti, A.; Shanbedi, M.; Zeinali, S. Heat transfer and rheological properties of transformer oil-oxidized MWCNT nanofluid. J. Therm. Anal. Calorim. 2014, 118, 1451–1460. [Google Scholar] [CrossRef]
- Larson, R.G. The rheology of dilute solutions of flexible polymers: Progress and problems. J. Rheol. 2005, 49, 1–70. [Google Scholar] [CrossRef]
- Kamal, C.; Gravelle, S.; Botto, L. Hydrodynamic slip can align thin nanoplatelets in shear flow. Nat. Commun. 2020, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Vajjha, R.S.; Das, D.K.; Chukwu, G.A. An Experimental Determination of the Viscosity of Propylene Glycol/Water Based Nanofluids and Development of New Correlations. J. Fluids Eng. 2015, 137, 081201. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die Dissociationswärme und den Einfluss der Temperatur auf den Dissociationsgrad. Z. Phys. Chem. 1889, 4, 96–116. [Google Scholar] [CrossRef] [Green Version]











| Nanoparticles | Purity (%) | Density (g/cm3) | Molecular Weight (g/mol) | Average Thickness (nm) | Specific Surface Area (m2/g) | Coefficient of Friction | Source |
|---|---|---|---|---|---|---|---|
| CAS-Reg. No.: 12138-09-9 WS2 Silver-Grey Crystalline Solid Powder | 99 | 7.5 | 248 | 90 | 30 | 0.03–0.07 | M K Impex Corp. Mississauga, ON, Canada |
| Material | Name | Chemical Formula | Molecular Weight (g/mol) | Density (g/cm3) | Type (-) | Source |
|---|---|---|---|---|---|---|
| Surfactants | SDS * | NaC12H25SO4 | 288.38 | 1.01 | Anionic | Fisher Scientific, Loughborough, UK |
| SDBS * | C18H29NaO3S | 348.48 | 1.06 | Anionic | ||
| CTAB * | C19H42BrN | 364.45 | 0.5 | Cationic | ||
| Base fluid | EG * | (CH12OH)2 | 62.07 | 1.11 | Organic | Sigma Aldrich, Subang Jaya, Malaysia |
| WS2 (Vol%) | Surfactant Concentration (vol%) | Maximum Mean Zeta Potential (mV) | |||||
|---|---|---|---|---|---|---|---|
| SDS | SDBS | CTAB | SDS | SDBS | CTAB | No Surfactant | |
| 0.005 | 2 | 0.5 | 2 | −51.7 ± 4.9 | −45.2 ± 2.1 | 42.3 ± 4.5 | −7.9 ± 1.3 |
| 0.01 | 2 | 1 | 2 | −35.6 ± 5.3 | −43.2 ± 2.3 | 40 ± 2.8 | −9.28 ± 1.8 |
| 0.02 | 2 | 2 | 2 | −35.9 ± 6.8 | −42.7 ± 2.3 | 31.6 ± 3.9 | −5.06 ± 0.5 |
| WS2 (Vol%) | Optimal Surfactant Concentration (vol%) | Maximum Thermal Conductivity Enhancement (%) | |||||
|---|---|---|---|---|---|---|---|
| SDS | SDBS | CTAB | SDS | SDBS | CTAB | No Surfactant | |
| T = 25 °C | |||||||
| 0.005 | 0.05 | 1 | 0.05 | 2.8 | 2.5 | 2.4 | 1.6 |
| 0.01 | 0.05 | 0.05 | 0.05 | 1.9 | 1.5 | 1.7 | 1.2 |
| 0.02 | 0.05 | 0.05 | 1 | 2.2 | 1.7 | 2 | 1.2 |
| T = 50 °C | |||||||
| 0.005 | 0.05 | 0.5 | 1 | 1.9 | 2.1 | 2.2 | −1.4 |
| 0.01 | 0.05 | 2 | 2 | 0.4 | 2.7 | −2.7 | −1.6 |
| 0.02 | 0.05 | 0.05 | 2 | −3.5 | 1.5 | 0.4 | −1.9 |
| T = 70 °C | |||||||
| 0.005 | 0.05 | 0.5 | 0.5 | 4.5 | 1.3 | 4.1 | 3.9 |
| 0.01 | 2 | 0.5 | 1 | 4.6 | 1 | 1.3 | 3.5 |
| 0.02 | 2 | 0.05 | 0.05 | 3.0 | 1.7 | 6.9 | 0.4 |
| Sample Description | Flow Point Stress (mPa) at G’ = G” | Resulting Remarks |
|---|---|---|
| Base fluid (EG) | No crossover | Very high loss factor with high fluidity over entire deformation range |
| 0.005 vol% WS2 | No crossover | G’ increased as compared to EG but still high fluidity over entire deformation range |
| 0.01 vol% WS2 | No crossover | |
| 0.02 vol% WS2 | No crossover | |
| 0.005 vol% Ws2 + 0.05 vol% SDS | 4.2 | Behaves strongly gel-like until 1.218% of deformation |
| 0.01 vol% Ws2 + 2 vol% SDS | No significant crossover | Oscillatory behavior followed by completely liquid-like over high deformation range |
| 0.02 vol% WS2 + 0.05 vol% SDS | No significant crossover | Oscillatory behavior followed by completely liquid-like over high deformation range |
| 0.02 vol% WS2 + 2 vol% SDS | No significant crossover | Weak gel behavior at low deformation followed by liquid behavior over high deformation range |
| 0.005 vol% Ws2 + 1 vol% SDBS | 3.548 | Behaves like weak gel until 1.646% of deformation |
| 0.01 vol% Ws2 + 2 vol% SDBS | 9.05 | Strong gel until 2.779% of deformation |
| 0.02 vol% Ws2 + 0.05 vol% SDBS | No significant crossover | Weak gel behavior at low deformation followed by liquid behavior over high deformation range |
| 0.005 vol% Ws2 + 0.5 vol% SDBS | No crossover | Very high loss factor with high fluidity over entire deformation range |
| 0.02 vol% Ws2 + 0.05 vol% CTAB | 8.289 | Weak gel until 1.095% of deformation |
| 0.005 vol% Ws2 + 0.5 vol% CTAB | 2.597 | Weak gel until 0.5343% of deformation |
| 0.005 vol% Ws2 + 1 vol% CTAB | 3.815 | Weak gel until 1.32% of deformation |
| 0.005 vol% Ws2 + 0.05 vol% CTAB | No crossover | Very high loss factor with high fluidity over entire deformation range |
| Sample Description | H–B Model | Bingham Model | |||||
|---|---|---|---|---|---|---|---|
| τo (mPa) | K (mPa.sn) | n (-) | R2 | τo (mPa) | μ (mPa.s) | R2 | |
| Base fluid (EG) | 1.5421 | 14.575 | 1.0013 | 0.99999 | 1.0866 | 14.658 | 0.99999 |
| 0.005 vol% WS2 | 1.6031 | 13.258 | 1.0034 | 0.99999 | 0.50148 | 13.46 | 0.99999 |
| 0.01 vol% WS2 | −0.77283 * | 13.735 | 0.99937 | 0.99999 | −0.56718 * | 13.697 | 0.99999 |
| 0.02 vol% WS2 | 1.4844 | 14.247 | 1.0018 | 0.99999 | 0.85551 | 14.363 | 0.99999 |
| 0.005 vol% WS2 + 0.05 vol% SDS | 3.4724 | 12.812 | 1.0052 | 0.99999 | 1.8621 | 13.106 | 0.99999 |
| 0.01 vol% WS2 + 2 vol% SDS | −0.49429 * | 14.836 | 0.99817 | 0.99999 | 0.14732 | 14.718 | 0.99999 |
| 0.02 vol% WS2 + 0.05 vol% SDS | −1.3374 * | 14.487 | 0.99677 | 1 | −0.23628 * | 14.284 | 1 |
| 0.02 vol% WS2 + 2 vol% SDS | −2.0203 * | 15.367 | 0.99483 | 0.99999 | −0.16437 * | 15.023 | 1 |
| 0.005 vol% WS2 + 1 vol% SDBS | −1.1213 * | 15.57 | 0.99524 | 0.9998 | 0.61465 | 15.249 | 0.99998 |
| 0.01 vol% WS2 + 2 vol% SDBS | −2.2094 * | 16.01 | 0.99384 | 0.99999 | 0.090188 | 15.584 | 0.99999 |
| 0.02 vol% WS2 + 0.05 vol% SDBS | 3.9121 | 14.659 | 1.0064 | 0.99998 | 1.6365 | 15.074 | 0.99999 |
| 0.005 vol% WS2 + 0.5 vol% SDBS | 0.18404 | 15.014 | 0.99904 | 1 | 0.52664 | 14.951 | 1 |
| 0.02 vol% WS2+ 0.05 vol% CTAB | 13.844 | 15.654 | 0.9931 | 0.99996 | 16.393 | 15.186 | 0.99995 |
| 0.005 vol% WS2 + 0.5 vol% CTAB | 1.6446 | 14.449 | 0.99751 | 0.99999 | 2.4965 | 14.292 | 0.99998 |
| 0.005 vol% WS2 + 1 vol% CTAB | 15.344 | 13.99 | 1.01 | 0.99997 | 11.846 | 14.62 | 0.99998 |
| 0.005 vol% WS2 + 0.05 vol% CTAB | −3.02 * | 15.146 | 0.99256 | 0.99998 | −0.41809 * | 14.66 | 0.99998 |
| Sample Description | Viscosity Enhancement/Reduction (%) | ||
|---|---|---|---|
| 25 °C | 50 °C | 70 °C | |
| 0.005 vol% WS2 | −8.2 | −6 | −4.7 |
| 0.01 vol% WS2 | −6.9 | −5.3 | −4 |
| 0.02 vol% WS2 | −2.1 | −0.2 | −1 |
| 0.005 vol% WS2 + 0.05 vol% SDS | −10.5 | −8.1 | −5.6 |
| 0.01 vol% WS2 + 2 vol% SDS | 0.11 | 4.9 | 3 |
| 0.02 vol% WS2 + 0.05 vol% SDS | −3.1 | −2.8 | −0.6 |
| 0.02 vol% WS2 + 2 vol% SDS | 2.1 | 3.2 | 1.9 |
| 0.005 vol% WS2 + 1 vol% SDBS | 3.3 | 3 | 1.9 |
| 0.01 vol% WS2 + 2 vol% SDBS | 5.7 | 6.4 | 6.7 |
| 0.02 vol% WS2 + 0.05 vol% SDBS | 3.1 | 3 | 2 |
| 0.005 vol% WS2 + 0.5 vol% SDBS | 1.5 | 1.4 | 0.8 |
| 0.02 vol% WS2 + 0.05 vol% CTAB | 4.9 | 3.6 | 2.9 |
| 0.005 vol% WS2 + 0.5 vol% CTAB | −2.3 | −2.3 | −2.7 |
| 0.005 vol% WS2 + 1 vol% CTAB | 1.8 | −0.9 | 1 |
| 0.005 vol% WS2 + 0.05 vol% CTAB | −0.7 | −0.7 | −0.8 |
| Sample Description | Arrhenius Equation Fitting Parameters | ||
|---|---|---|---|
| Ea (Jmol−1) | R2 | ||
| Base fluid (EG) | 33.33762 | 0.27004 | 0.99723 |
| 0.005 vol% WS2 | 29.80826 | 0.2618 | 0.99712 |
| 0.01 vol% WS2 | 30.40985 | 0.26392 | 0.99712 |
| 0.02 vol% WS2 | 32.17606 | 0.26519 | 0.99796 |
| 0.005 vol% WS2 + 0.05 vol% SDS | 28.97151 | 0.26066 | 0.9968 |
| 0.01 vol% WS2 + 2 vol% SDS | 32.46486 | 0.26107 | 0.99781 |
| 0.02 vol% WS2 + 0.05 vol% SDS | 32.11054 | 0.26817 | 0.99685 |
| 0.02 vol% WS2 + 2 vol% SDS | 33.89205 | 0.26831 | 0.99794 |
| 0.005 vol% WS2 + 1 vol% SDBS | 34.6949 | 0.2721 | 0.99738 |
| 0.01 vol% WS2 + 2 vol% SDBS | 34.98507 | 0.26773 | 0.99721 |
| 0.02 vol% WS2 + 0.05 vol% SDBS | 34.60862 | 0.27182 | 0.9976 |
| 0.005 vol% WS2 + 0.5 vol% SDBS | 33.89232 | 0.27049 | 0.99729 |
| 0.02 vol% WS2 + 0.05 vol% CTAB | 35.27397 | 0.27409 | 0.99646 |
| 0.005 vol% WS2 + 0.5 vol% CTAB | 32.54759 | 0.26995 | 0.99732 |
| 0.005 vol% WS2 + 1 vol% CTAB | 34.31033 | 0.27608 | 0.99499 |
| 0.005 vol% WS2 + 0.05 vol% CTAB | 33.16464 | 0.27049 | 0.9973 |
| Sample Description | Thermal Conductivity Enhancement/Reduction | Viscosity Reduction | Particle Size | Zeta Potential | |||||
|---|---|---|---|---|---|---|---|---|---|
| (%) | (%) | (nm) | (−mV) | ||||||
| 25 °C | 50 °C | 70 °C | 25 °C | 50 °C | 70 °C | 25 °C | |||
| 0.005 vol% WS2 | 1.6 | −1.4 | 3.9 | −8.2 | −6 | −4.7 | 378.28 ± 34.3 | 7.9 ± 1.3 | |
| 0.01 vol% WS2 | 1.2 | −1.6 | 3.5 | −6.9 | −5.3 | −4 | 335.81 ± 38.9 | 9.28 ± 1.8 | |
| 0.02 vol% WS2 | 1.2 | −1.9 | 0.4 | −2.1 | −0.2 | −1 | 388.8 ± 25.7 | 5.06 ± 0.5 | |
| 0.005 vol% WS2 + 0.05 vol% SDS | 2.8 | 1.9 | 4.5 | −10.5 | −8.1 | −5.6 | 749.2 ± 50.1 | 14.9 ± 1.5 | |
| 0.02 vol% WS2 + 0.05 vol% SDS | 2.2 | −3.5 | 3 | −3.1 | −2.8 | −0.6 | 1224.6 ± 65.3 | 8.7 ± 1.1 | |
| 0.005 vol% WS2 + 0.5 vol% CTAB | 2.3 | 0.2 | 4.1 | −2.3 | −2.3 | −2.7 | 532.8 ± 28.4 | −22 ± 2.6 | |
| 0.005 vol% WS2 + 0.05 vol% CTAB | 2.4 | −0.6 | −2.4 | −0.7 | −0.7 | −0.8 | 338.4 ± 10.2 | 5.8 ± 0.5 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, S.N.A.; Shahabuddin, S.; Mohd Sabri, M.F.; Mohd Salleh, M.F.; Mohd Said, S.; Khedher, K.M.; Sridewi, N. Two-Dimensional Tungsten Disulfide-Based Ethylene Glycol Nanofluids: Stability, Thermal Conductivity, and Rheological Properties. Nanomaterials 2020, 10, 1340. https://doi.org/10.3390/nano10071340
Shah SNA, Shahabuddin S, Mohd Sabri MF, Mohd Salleh MF, Mohd Said S, Khedher KM, Sridewi N. Two-Dimensional Tungsten Disulfide-Based Ethylene Glycol Nanofluids: Stability, Thermal Conductivity, and Rheological Properties. Nanomaterials. 2020; 10(7):1340. https://doi.org/10.3390/nano10071340
Chicago/Turabian StyleShah, Syed Nadeem Abbas, Syed Shahabuddin, Mohd Faizul Mohd Sabri, Mohd Faiz Mohd Salleh, Suhana Mohd Said, Khaled Mohamed Khedher, and Nanthini Sridewi. 2020. "Two-Dimensional Tungsten Disulfide-Based Ethylene Glycol Nanofluids: Stability, Thermal Conductivity, and Rheological Properties" Nanomaterials 10, no. 7: 1340. https://doi.org/10.3390/nano10071340
APA StyleShah, S. N. A., Shahabuddin, S., Mohd Sabri, M. F., Mohd Salleh, M. F., Mohd Said, S., Khedher, K. M., & Sridewi, N. (2020). Two-Dimensional Tungsten Disulfide-Based Ethylene Glycol Nanofluids: Stability, Thermal Conductivity, and Rheological Properties. Nanomaterials, 10(7), 1340. https://doi.org/10.3390/nano10071340