Molecular Dynamics Simulation for the Effect of Fluorinated Graphene Oxide Layer Spacing on the Thermal and Mechanical Properties of Fluorinated Epoxy Resin
Abstract
:1. Introduction
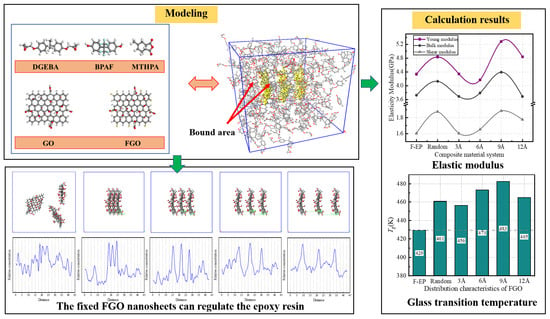
2. Model Construction and Simulation Calculation
3. Results and Discussion
3.1. Static Mechanical Performance Calculation
3.2. Thermal Performance Analysis
3.2.1. Glass Transition Temperature
3.2.2. Coefficient of Thermal Expansion
3.2.3. Thermal Conductivity
3.3. Microscopic Parameter Calculation and Principle Discussion
3.3.1. Free Volume
3.3.2. Mean Square Displacement
3.3.3. Axial Density Distribution
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Thomas, R.; Ding, Y.M.; He, Y.L.; Yang, L.; Moldenaers, P.; Yang, W.M.; Czigany, T.; Thomas, S. Miscibility, morphology, thermal, and mechanical properties of a DGEBA based epoxy resin toughened with a liquid rubber. Polymer 2008, 49, 278–294. [Google Scholar] [CrossRef]
- Gu, J.W.; Liang, C.B.; Zhao, X.M.; Gan, B.; Qiu, H.; Guo, Y.Q.; Yang, X.T.; Zhang, Q.Y.; Wang, D.Y. Highly thermally conductive flame-retardant epoxy nanocomposites with reduced ignitability and excellent electrical conductivities. Compos. Sci. Technol. 2017, 139, 83–89. [Google Scholar] [CrossRef]
- Zhao, Y.S.; He, Y.H.; Yang, K.R.; Wang, X.P.; Bai, J.H.; Du, B. Improving the Surface Insulating Performance of Epoxy Resin/Al2O3 Composite Materials by Extending Chain of Liquid Epoxy Resin with Me-THPA. High Volt. 2019, 5, 472–481. [Google Scholar] [CrossRef]
- Xie, Q.; Fu, K.X.; Liang, S.D.; Liu, B.W.; Lu, L.; Yang, X.M.; Huang, Z.Y.; Lu, F.C. Micro-Structure and Thermomechanical Properties of Crosslinked Epoxy Composite Modified by Nano-SiO2: A Molecular Dynamics Simulation. Polymer 2018, 10, 801. [Google Scholar] [CrossRef] [Green Version]
- Barbosa, A.P.C.; Fulco, A.P.P.; Guerra, E.S.S.; Arakaki, F.K.; Tosatto, M.; Costa, M.C.B.; Melo, J.D.D. Accelerated aging effects on carbon fiber/epoxy composites. Compos. Part B Eng. 2016, 110, 298–306. [Google Scholar] [CrossRef]
- Mondal, N.; Haque, N.; Dalai, S.; Chakravorti, S.; Chatterjee, B. A Method for Identifying Ageing in Epoxy-mica Composite Insulation used in Rotational machines through Modelling of Dielectric Relaxation. High Volt. 2020, 5, 184–190. [Google Scholar] [CrossRef]
- Brostow, W.; Chonkaew, W.; Menard, K.P.; Scharf, T.W. Modification of an epoxy resin with a fluoroepoxy oligomer for improved mechanical and tribological properties. Mat. Sci. Eng. 2009, 507, 241–251. [Google Scholar] [CrossRef]
- Hou, D.F.; Ma, H.B.; Li, X.Y.; He, J.; Liao, H.W. Preparation and properties of 4,4′-(hexafluoroisopropylidene) diphenol cured 2,2-bis(4-cyanatophenyl) propane. J. Appl. Polym. Sci. 2017, 134, 44518. [Google Scholar] [CrossRef]
- Taa, Z.Q.; Yang, S.Y.; Ge, Z.Y.; Chen, J.S.; Fan, L. Synthesis and properties of novel fluorinated epoxy resins based on 1,1-bis(4-glycidylesterphenyl)-1-(3′-trifluoromethylphenyl)-2,2,2-trifluoroethane. Eur. Polym. J. 2007, 43, 550–560. [Google Scholar] [CrossRef]
- Wan, Y.J.; Tang, L.C.; Gong, L.X.; Yan, D.; Li, Y.B.; Wu, L.B.; Jiang, J.X.; Lai, G.Q. Grafting of epoxy chains onto graphene oxide for epoxy composites with improved mechanical and thermal properties. Carbon 2014, 69, 467–480. [Google Scholar] [CrossRef]
- Shirasu, K.; Kitayama, S.; Liu, F.; Yamamoto, G.; Hashida, T. Molecular Dynamics Simulations and Theoretical Model for Engineering Tensile Properties of Single-and Multi-Walled Carbon Nanotubes. Nanomaterials 2021, 11, 795. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Lu, R.G.; Su, C.; Wang, H.N.; Guo, Z.; Liu, P.; Huang, Z.Y.; Chen, H.M.; Li, T.S. Chemically modified graphene/polyimide composite films based on utilization of covalent bonding and oriented distribution. ACS Appl. Mater. Interfaces 2012, 4, 2699–2708. [Google Scholar] [CrossRef] [PubMed]
- Fang, F.; Ran, S.Y.; Fang, Z.P.; Song, P.G.; Wang, H. Improved flame resistance and thermo-mechanical properties of epoxy resin nanocomposites from functionalized graphene oxide via self-assembly in water. Composites 2019, 165, 406–416. [Google Scholar] [CrossRef]
- McAllister, M.J.; Li, J.L.; Adamson, D.H.; Schniepp, H.C.; Abdala, A.A.; Liu, J.; Herrera-Alonso, M.; Milius, D.L.; Car, R.; Prud’homme, R.K.; et al. Single sheet functionalized graphene by oxidation and thermal expansion of graphite. Chem. Mater. 2007, 19, 4396–4404. [Google Scholar] [CrossRef]
- Kim, H.; Miura, Y.; Macosko, C.W. Graphene/Polyurethane Nanocomposites for Improved Gas Barrier and Electrical Conductivity. Chem. Mater. 2010, 22, 3441–3450. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, Z. Graphene in Ionic Liquids: Collective van der Waals Interaction and Hindrance of Self-Assembly Pathway. J. Phys. Chem. B 2013, 117, 10540–10547. [Google Scholar] [CrossRef]
- Lin, S.; Shih, C.J.; Strano, M.S.; Blankschtein, D. Molecular Insights into the Surface Morphology, Layering Structure, and Aggregation Kinetics of Surfactant-Stabilized Graphene Dispersions. J. Am. Chem. Soc. 2011, 133, 12810–12823. [Google Scholar] [CrossRef] [PubMed]
- Lü, F.; Zhan, Z.; Zhang, G.; Jiao, Y.; Xie, Q. Effect of Plasma Fluorinated Modified Micron AlN Filling on Insulation Properties of Epoxy Resin. Trans. China Electrotech. Soc. 2019, 34, 3522–3531. [Google Scholar]
- Wu, H.; Xie, Q.; Duan, Q.; Yan, J.; Yin, K. Plasma fluorination of BaTiO3 for enhancement ofinterfacial adhesion and surface insulation of epoxy resin. J. Mater. Sci. 2020, 4, 1499–1510. [Google Scholar] [CrossRef]
- Lu, F.; Ruan, H.; Song, J.; Yin, K.; Zhan, Z.; Jiao, Y.; Xie, Q. Enhanced surface insulation and depressed dielectricconstant for Al2O3/epoxy composites through plasma fluorination of filler. J. Phys. D Appl. Phys. 2019, 52, 155201. [Google Scholar] [CrossRef]
- Yang, X.; Yu, D.; Cao, B.; To, A. Ultrahigh Thermal Rectification in Pillared Graphene Structure with Carbon Nanotube–Graphene Intramolecular Junctions. ACS Appl. Mater. Interfaces 2017, 9, 29–35. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, C.; Pei, Q.; Zhang, Y. Some Aspects of Thermal Transport across the Interface between Graphene and Epoxy in Nanocomposites. ACS Appl. Mater. Interfaces 2016, 8, 8272–8279. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Ginzburg, V.V.; Yang, J.; Yang, Y.; Liu, W.; Huang, Y.; Du, L.; Chen, B. Thermal Conductivity of Polymer-Based Composites: Fundamentals and Applications. Prog. Polym. Sci. 2016, 59, 41–85. [Google Scholar] [CrossRef]
- Yousefi, N.; Sun, X.; Lin, X.; Shen, X.; Jia, J.; Zhang, B.; Tang, B.; Chan, M.; Kim, J.K. Highly Aligned Graphene/Polymer Nanocomposites with Excellent Dielectric Properties for High Performance Electromagnetic Interference Shielding. Adv. Mater. 2015, 26, 5480–5487. [Google Scholar] [CrossRef] [PubMed]
- Fang, M.; Hao, Y.; Ying, Z.; Wang, H.; Cheng, H.; Zeng, Y. Controllable edge modification of multi-layer graphene for improved dispersion stability and high electrical conductivity. Appl. Nanosci. 2019, 9, 469–477. [Google Scholar] [CrossRef]
- Xiao, C.; Guo, Y.; Tang, Y.; Ding, J.; Zhang, X.; Zheng, K.; Tian, X. Epoxy composite with significantly improved thermal conductivity by constructing a vertically aligned three-dimensional network of silicon carbide nanowires/boron nitride nanosheets. Compos. Part B Eng. 2020, 187, 107855. [Google Scholar] [CrossRef]
- Kumar, S.K.; Ganesan, V.; Riggleman, R.A. Perspective: Outstanding theoretical questions in polymer-nanoparticle hybrids. J. Chem. Phys. 2017, 147, 020901. [Google Scholar] [CrossRef] [Green Version]
- Jabbarzadeh, A.; Halfina, B. Unravelling the effects of size, volume fraction and shape of nanoparticle additives on crystallization of nanocomposite polymers. Nanoscale Adv. 2019, 1, 4704. [Google Scholar] [CrossRef] [Green Version]
- Jabbarzadeh, A. The Origins of Enhanced and Retarded Crystallization in Nanocomposite Polymers. Nanomaterials 2019, 9, 1472. [Google Scholar] [CrossRef] [Green Version]
- Yousefi, N.; Gudarzi, M.M.; Zheng, Q.; Aboutalebi, S.H.; Sharif, F.; Kim, J.K. Self-alignment and high electrical conductivity of ultralarge graphene oxide–polyurethane nanocomposites. J. Mater. Chem. A 2012, 22, 12709–12717. [Google Scholar] [CrossRef]
- Yousefi, N.; Gudarzi, M.M.; Zheng, Q.; Lin, X.; Shen, X.; Jia, J.; Sharif, F.; Kim, J.K. Highly aligned, ultralarge-size reduced graphene oxide/polyurethane nanocomposites: Mechanical properties and moisture permeability. Compos. Part A Appl. Sic. Manuf. 2013, 49, 42–50. [Google Scholar] [CrossRef]
- Li, Q.; Huang, X.; Liu, T.; Yan, J.; Wang, Z.; Zhang, Y.; Lu, X. Advances in application of molecular simulation technology in high voltage insulation. Trans. China Electrotech. Soc. 2016, 31, 1–13. [Google Scholar]
- Yang, Q.; Li, X.; Shi, L.; Yang, X.; Sui, G. The thermal characteristics of epoxy resin: Design and predict by using molecular simulation method. Polymer 2013, 54, 6447–6454. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, X.; Xiao, S.; Wen, H.; Wu, Y. Molecular dynamics simulation of thermodynamic properties of modified SiO2 epoxy resin. High Volt. Technol. 2018, 44, 740–749. [Google Scholar]
- Damasceno, D.A.; Rajapakse, R.; Mesquita, E. Atomistic Modelling of Size-Dependent Mechanical Properties and Fracture of Pristine and Defective Cove-Edged Graphene Nanoribbons. Nanomaterials 2020, 10, 1422. [Google Scholar] [CrossRef]
- Chowdhury, S.C.; Prosser, R.; Sirk, T.W.; Elder, R.M.; Gillespie, J.W. Glass fiber-epoxy interactions in the presence of silane: A molecular dynamics study. Appl. Surf. Sci. 2020, 542, 148738. [Google Scholar] [CrossRef]
- Zhang, W.; Qing, Y.; Zhong, W.; Sui, G.; Yang, X.P. Mechanism of modulus improvement for epoxy resin matrices: A molecular dynamics simulation. React. Funct. Polym. 2017, 111, 60–67. [Google Scholar] [CrossRef]
- Hadden, C.M.; Klimek-Mcdonald, D.R.; Pineda, E.J.; King, J.A.; Reichanadter, A.M.; Miskioglu, I.; Gowtham, S.; Odegard, G.M. Mechanical properties of graphene nanoplatelet/carbon fiber/epoxy hybrid composites: Multiscale modeling and experiments. Carbon 2015, 95, 100–112. [Google Scholar] [CrossRef] [Green Version]
- Shenogina, N.B.; Tsige, M.; Patnaik, S.S.; Mukhopadhyay, S.M. Molecular Modeling Approach to Prediction of Thermo-Mechanical Behavior of Thermoset Polymer Networks. Macromolecules 2012, 45, 5307–5315. [Google Scholar] [CrossRef]
- Wang, T.Y.; Tseng, P.Y.; Tasi, J.L. Characterization of Young’s modulus and thermal conductivity of graphene/epoxy nanocomposites. J. Compos. Mater. 2019, 53, 835–847. [Google Scholar] [CrossRef]
- Yang, K.R.; Zhao, Y.S.; Zhang, S.; He, Y.H.; Wang, X.P. Study on Thermal and Electrical Properties of BPAF Modified Epoxy/Al2O3 Composites. In Proceedings of the 2019 2nd International Conference on Electrical Materials and Power Equipment (ICEMPE), Guangzhou, China, 7–10 April 2019; pp. 277–280. [Google Scholar]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B Condens. Matter. 1989, 39, 5566–5568. [Google Scholar] [CrossRef] [PubMed]
- Shokuhfar, A.; Arab, B. The effect of cross linking density on the mechanical properties and structure of the epoxy polymers: Molecular dynamics simulation. J. Mol. Modeling 2013, 19, 3719–3731. [Google Scholar] [CrossRef]
- Jeyranpour, F.; Alahyarizadeh, G.; Minuchehr, A. The thermo-mechanical properties estimation of fullerene-reinforced resin epoxy composites by molecular dynamics simulation–A comparative study. Polymer 2016, 88, 9–18. [Google Scholar] [CrossRef]
- Choi, J.; Yu, S.; Yang, S.; Cho, M. The glass transition and thermoelastic behavior of epoxy-based nanocomposites: A molecular dynamics study. Polymer 2011, 52, 5197–5203. [Google Scholar] [CrossRef]
- Müller-Plathe, F. A simple nonequilibrium molecular dynamics method for calculating the thermal conductivity. J. Chem. Phys. 1997, 106, 6082–6085. [Google Scholar] [CrossRef]
- Li, S.H.; Yu, X.X.; Bao, H.; Yang, N. High thermal conductivity of bulk epoxy resin by bottom-up parallel-linking and strain: A molecular dynamics study. Indian J. Chem. A 2018, 122, 13140–13147. [Google Scholar] [CrossRef] [Green Version]
- Fox, T.G. Second-order transition temperatures and related properties of polystyrene. I. influence of molecular weight. J. Appl. Phys. 1950, 6, 581–591. [Google Scholar] [CrossRef]
- Wei, Q.H.; Zhang, Y.F.; Wang, Y.E.; Yang, M.M. A molecular dynamic simulation method to elucidate the interaction mechanism of nano-SiO2 in polymer blends. J. Mater. Sci. 2017, 52, 12889–12901. [Google Scholar] [CrossRef]
- Li, K.; Li, Y.; Lian, Q.S.; Cheng, J.; Zhang, J.Y. Influence of cross-linking density on the structure and properties of the interphase within supported ultrathin epoxy films. J. Mater. Sci. 2016, 51, 9019–9030. [Google Scholar] [CrossRef]










| System | Layer Spacing (Å) | Number of Molecules | |||
|---|---|---|---|---|---|
| FGO | DGEBA | MTHPA | BPAF | ||
| F-EP | – | 0 | 50 | 100 | 25 |
| Random | – | 3 | 50 | 100 | 25 |
| 3-FGO/F-EP | 3 | 3 | 50 | 100 | 25 |
| 6-FGO/F-EP | 6 | 3 | 50 | 100 | 25 |
| 9-FGO/F-EP | 9 | 3 | 50 | 100 | 25 |
| 12-FGO/F-EP | 12 | 3 | 50 | 100 | 25 |
| System | Eresin | Efiber | Etotal | Einterface |
|---|---|---|---|---|
| GO/F-EP | −4761 | −769 | −4157 | 1373 |
| FGO/F-EP | −4761 | −805 | −3766 | 1799 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, Q.; Xie, J.; Xia, G.; Xiao, C.; Yang, X.; Xie, Q.; Huang, Z. Molecular Dynamics Simulation for the Effect of Fluorinated Graphene Oxide Layer Spacing on the Thermal and Mechanical Properties of Fluorinated Epoxy Resin. Nanomaterials 2021, 11, 1344. https://doi.org/10.3390/nano11051344
Duan Q, Xie J, Xia G, Xiao C, Yang X, Xie Q, Huang Z. Molecular Dynamics Simulation for the Effect of Fluorinated Graphene Oxide Layer Spacing on the Thermal and Mechanical Properties of Fluorinated Epoxy Resin. Nanomaterials. 2021; 11(5):1344. https://doi.org/10.3390/nano11051344
Chicago/Turabian StyleDuan, Qijun, Jun Xie, Guowei Xia, Chaoxuan Xiao, Xinyu Yang, Qing Xie, and Zhengyong Huang. 2021. "Molecular Dynamics Simulation for the Effect of Fluorinated Graphene Oxide Layer Spacing on the Thermal and Mechanical Properties of Fluorinated Epoxy Resin" Nanomaterials 11, no. 5: 1344. https://doi.org/10.3390/nano11051344
APA StyleDuan, Q., Xie, J., Xia, G., Xiao, C., Yang, X., Xie, Q., & Huang, Z. (2021). Molecular Dynamics Simulation for the Effect of Fluorinated Graphene Oxide Layer Spacing on the Thermal and Mechanical Properties of Fluorinated Epoxy Resin. Nanomaterials, 11(5), 1344. https://doi.org/10.3390/nano11051344