Simultaneous Improvement of Yield Strength and Ductility at Cryogenic Temperature by Gradient Structure in 304 Stainless Steel
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussions

4. Conclusions
- (1).
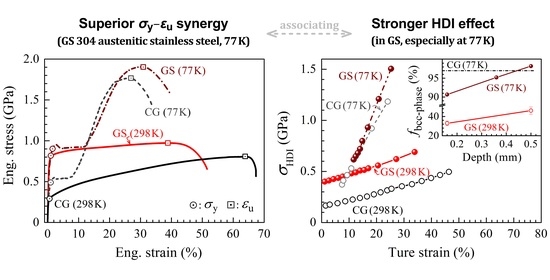
- Compared to the homogeneous CG sample, excellent synergy of strength and ductility was obtained by the gradient structures at room temperature. Moreover, simultaneous improvement of the yield strength and the uniform elongation was induced by the gradient structures at cryogenic temperature, as compared to the homogeneous CG sample.
- (2).
- The HDI hardening was found to play a more important role in the gradient structures as compared to the homogeneous CG sample at both room and cryogenic temperatures, resulting in better tensile properties in the gradient structures. The HDI hardening was also found to be much more obvious at cryogenic temperature as compared to that at room temperature.
- (3).
- In the gradient structures, the central layer provides stronger strain hardening during tensile deformation at both room and cryogenic temperatures, as compared to the surface layer. The volume fraction of martensitic transformation was found to increase along the depth from the surface layer to the central layer during tensile deformation at both room and cryogenic temperatures for the gradient structures. The cryogenic deformation was found to induce more volume fraction of martensitic transformation at each depth in the gradient structures as compared to the room temperature deformation, resulting in a much stronger strain hardening at cryogenic temperature.
- (4).
- The dislocation density and the amount of martensitic transformation are observed to be higher at the central layer of the gradient structures as compared to the CG sample, which are the origins for the simultaneous improvement strength and ductility by the gradient structures at the cryogenic temperature. The present findings should provide insights for tailoring heterogeneous microstructures to achieve excellent synergy of strength and ductility/toughness at both room and cryogenic temperatures in metals and alloys.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Morris, J.W. Stronger, tougher steels. Science 2008, 320, 1022–1023. [Google Scholar] [CrossRef] [PubMed]
- Militzer, M. A Synchrotron look at steel. Science 2002, 298, 975–976. [Google Scholar] [CrossRef] [PubMed]
- Koch, C.C.; Morris, D.G.; Lu, K.; Inoue, A. Ductility of nanostructured materials. MRS Bull. 1999, 24, 54–58. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Liao, X. Retaining ductility. Nat. Mater. 2004, 3, 351–352. [Google Scholar] [CrossRef] [PubMed]
- Lu, K. Making strong nanomaterials ductile with gradients. Science 2014, 345, 1455–1456. [Google Scholar] [CrossRef] [PubMed]
- Ma, E.; Wu, X. Tailoring Heterogeneities in high-entropy alloys to promote strength–ductility synergy. Nat. Commun. 2019, 10, 5623. [Google Scholar] [CrossRef] [Green Version]
- Fang, T.H.; Li, W.L.; Tao, N.R.; Lu, K. Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper. Science 2011, 331, 1587–1590. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Jiang, P.; Chen, L.; Yuan, F.; Zhu, Y.T. Extraordinary strain hardening by gradient structure. Proc. Natl. Acad. Sci. USA 2014, 111, 7197–7201. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Yang, M.; Yuan, F.; Wu, G.; Wei, Y.; Huang, X.; Zhu, Y. Heterogeneous lamella structure unites ultrafine-grain strength with coarse-grain ductility. Proc. Natl. Acad. Sci. USA 2015, 112, 14501–14505. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Fan, G.; Huang, X.; Juul Jensen, D.; Miao, K.; Xu, C.; Geng, L.; Zhang, Y.; Yu, T. Enhanced strength in pure Ti via design of alternating coarse- and fine-grain layers. Acta Mater. 2021, 206, 116627. [Google Scholar] [CrossRef]
- He, B.B.; Hu, B.; Yen, H.W.; Cheng, G.J.; Wang, Z.K.; Luo, H.W.; Huang, M.X. High dislocation density–induced large ductility in deformed and partitioned steels. Science 2017, 357, 1029–1032. [Google Scholar] [CrossRef] [Green Version]
- Mao, Q.; Zhang, Y.; Guo, Y.; Zhao, Y. Enhanced electrical conductivity and mechanical properties in thermally stable fine-grained copper wire. Commun. Mater. 2021, 2, 1–9. [Google Scholar] [CrossRef]
- Yang, M.; Yan, D.; Yuan, F.; Jiang, P.; Ma, E.; Wu, X. Dynamically reinforced heterogeneous grain structure prolongs ductility in a medium-entropy alloy with gigapascal yield strength. Proc. Natl. Acad. Sci. USA 2018, 115, 7224–7229. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Cao, Y.; Mao, Q.; Zhou, H.; Zhao, Y.; Jiang, W.; Liu, Y.; Wang, J.T.; You, Z.; Zhu, Y. Critical microstructures and defects in heterostructured materials and their effects on mechanical properties. Acta Mater. 2020, 189, 129–144. [Google Scholar] [CrossRef]
- Wu, X.; Yuan, F.; Yang, M.; Jiang, P.; Zhang, C.; Chen, L.; Wei, Y.; Ma, E. Nanodomained nickel unite nanocrystal strength with coarse-grain ductility. Sci. Rep. 2015, 5, 11728. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Chen, X.; Huang, X.; Lu, K. Revealing the maximum strength in nanotwinned copper. Science 2009, 323, 607–610. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhou, H.; Lu, Q.; Gao, H.; Lu, L. Extra strengthening and work Hardening in gradient nanotwinned metals. Science 2018, 362, eaau1925. [Google Scholar] [CrossRef] [Green Version]
- Tang, S.; Xin, T.; Xu, W.; Miskovic, D.; Sha, G.; Quadir, Z.; Ringer, S.; Nomoto, K.; Birbilis, N.; Ferry, M. Precipitation strengthening in an ultralight magnesium alloy. Nat. Commun. 2019, 10, 1003. [Google Scholar] [CrossRef]
- Peng, S.; Wei, Y.; Gao, H. Nanoscale precipitates as sustainable dislocation sources for enhanced ductility and high strength. Proc. Natl. Acad. Sci. USA 2020, 117, 5204–5209. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Pan, J.; Zhou, H.F.; Gao, H.J.; Li, Y. Mechanical properties and optimal grain size distribution profile of gradient grained nickel. Acta Mater. 2018, 153, 279–289. [Google Scholar] [CrossRef]
- Wu, X.L.; Jiang, P.; Chen, L.; Zhang, J.F.; Yuan, F.P.; Zhu, Y.T. Synergetic strengthening by gradient structure. Mater. Res. Lett. 2014, 2, 185–191. [Google Scholar] [CrossRef]
- Hasan, M.N.; Liu, Y.F.; An, X.H.; Gu, J.; Song, M.; Cao, Y.; Li, Y.S.; Zhu, Y.T.; Liao, X.Z. Simultaneously enhancing strength and ductility of a high-entropy alloy via gradient hierarchical microstructures. Int. J. Plast. 2019, 123, 178–195. [Google Scholar] [CrossRef]
- Li, X.; Lu, L.; Li, J.; Zhang, X.; Gao, H. Mechanical properties and deformation mechanisms of gradient nanostructured metals and alloys. Nat. Rev. Mater. 2020, 5, 706–723. [Google Scholar] [CrossRef]
- Zoubi, W.A.; Kamil, M.P.; Fatimah, S.; Nashrah, N.; Ko, Y.G. Recent advances in hybrid organic-inorganic materials with spatial architecture for state-of-the-art applications. Prog. Mater. Sci. 2020, 112, 100663. [Google Scholar] [CrossRef]
- Zoubi, W.A.; Kim, M.J.; Kim, Y.G.; Ko, Y.G. Dual-functional crosslinked polymer-inorganic materials for robust electrochemical performance and antibacterial activity. Chem. Eng. J. 2020, 392, 123654. [Google Scholar] [CrossRef]
- Zoubi, W.A.; Putri, R.A.K.; Ko, Y.G. Understanding the metal ion-ligand responsible in the plasma-assisted electrochemical reactions for optimizing chemical stability. J. Mol. Liq. 2021, 321, 114756. [Google Scholar] [CrossRef]
- Lu, K.; Yan, F.K.; Wang, H.T.; Tao, N.R. Strengthening austenitic steels by using nanotwinned austenitic grains. Scr. Mater. 2012, 66, 878–883. [Google Scholar] [CrossRef]
- Lu, L.; You, Z.S.; Lu, K. Work hardening of polycrystalline Cu with nanoscale twins. Scr. Mater. 2012, 66, 837–842. [Google Scholar] [CrossRef]
- Ashby, M.F. The Deformation of plastically non-homogeneous materials. Philos. Mag. J. Theor. Exp. Appl. Phys. 1970, 21, 399–424. [Google Scholar] [CrossRef]
- Zhu, Y.; Wu, X. Perspective on hetero-deformation induced (HDI) hardening and back stress. Mater. Res. Lett. 2019, 7, 393–398. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.F.; Huang, C.X.; Fang, X.T.; Höppel, H.W.; Göken, M.; Zhu, Y.T. Hetero-deformation induced (HDI) hardening does not increase linearly with strain gradient. Scr. Mater. 2020, 174, 19–23. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.; Xu, D.; Lu, L.; Gao, H.; Zhu, T. Gradient plasticity in gradient nano-grained metals. Extreme Mech. Lett. 2016, 8, 213–219. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Lu, X.; Yuan, F.; Kan, Q.; Qu, S.; Kang, G.; Zhang, X. Multiple mechanism based constitutive modeling of gradient nanograined material. Int. J. Plast. 2020, 125, 314–330. [Google Scholar] [CrossRef]
- Wu, X.L.; Yang, M.X.; Yuan, F.P.; Chen, L.; Zhu, Y.T. Combining gradient structure and TRIP effect to produce austenite stainless steel with high strength and ductility. Acta Mater. 2016, 112, 337–346. [Google Scholar] [CrossRef] [Green Version]
- Fan, J.; Zhu, L.; Lu, J.; Fu, T.; Chen, A. Theory of designing the gradient microstructured metals for overcoming strength-ductility trade-off. Scr. Mater. 2020, 184, 41–45. [Google Scholar] [CrossRef]
- Chen, A.; Liu, J.; Wang, H.; Lu, J.; Wang, Y.M. Gradient twinned 304 stainless steels for high strength and high ductility. Mater. Sci. Eng. A 2016, 667, 179–188. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Wen, C.; Gao, C.; Guo, X.; Chen, Z.; Lu, J. Static and dynamic mechanical behaviors of gradient-nanotwinned stainless steel with a composite structure: Experiments and modeling. Int. J. Plast. 2019, 114, 272–288. [Google Scholar] [CrossRef]
- He, J.; Yuan, F.; Yang, M.; Zhou, L.; Jiao, S.; Wu, X. Exceptional tensile properties under cryogenic temperature in heterogeneous laminates induced by non-uniform martensitic transformation and strain delocalization. Mater. Sci. Eng. A 2020, 791, 139780. [Google Scholar] [CrossRef]
- Park, W.S.; Yoo, S.W.; Kim, M.H.; Lee, J.M. Strain-rate effects on the mechanical behavior of the AISI 300 series of austenitic stainless steel under cryogenic environments. Mater. Des. 2010, 31, 3630–3640. [Google Scholar] [CrossRef]
- Lu, Y.; Hui, H. Investigation on mechanical properties of S30403 austenitic stainless steel at different temperatures. J. Press. Vessel Technol. 2018, 140, 024502. [Google Scholar] [CrossRef]
- Hauser, M.; Wendler, M.; Fabrichnaya, O.; Volkova, O.; Mola, J. Anomalous stabilization of austenitic stainless steels at cryogenic temperatures. Mater. Sci. Eng. A 2016, 675, 415–420. [Google Scholar] [CrossRef]
- Grässel, O.; Krüger, L.; Frommeyer, G.; Meyer, L.W. High strength Fe-Mn-(Al, Si) TRIP/TWIP steels development-properties-application. Int. J. Plast. 2000, 16, 1391–1409. [Google Scholar] [CrossRef]
- He, J.; Ma, Y.; Yan, D.; Jiao, S.; Yuan, F.; Wu, X. Improving ductility by increasing fraction of interfacial zone in low C steel/304 ss laminates. Mater. Sci. Eng. A 2018, 726, 288–297. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Britton, T.B.; Wilkinson, A.J. Measurement of geometrically necessary dislocation density with high resolution electron backscatter diffraction: Effects of detector binning and step size. Ultramicroscopy 2013, 125, 1–9. [Google Scholar] [CrossRef]
- Brough, I.; Bate, P.S.; Humphreys, F.J. Optimising the angular resolution of EBSD. Mater. Sci. Technol. 2006, 22, 1279–1286. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.Y.; Lu, K. Enhanced thermal stability of nanograined metals below a critical grain size. Science 2018, 360, 526–530. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; He, Y.; Cai, S. Gradient recrystallization to improve strength and ductility of medium-entropy alloy. J. Alloys Compd. 2021, 853, 157388. [Google Scholar] [CrossRef]
- Gao, H.; Huang, Y.; Nix, W.D.; Hutchinson, J.W. Mechanism-based strain gradient plasticity—I. theory. J. Mech. Phys. Solids 1999, 47, 1239–1263. [Google Scholar] [CrossRef]
- Kubin, L.P.; Mortensen, A. Geometrically necessary dislocations and strain-gradient plasticity: A few critical issues. Scr. Mater. 2003, 48, 119–125. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.H.; Kim, S.K.; Kim, M.H.; Lee, J.M. Numerical model to predict deformation of corrugated austenitic stainless steel sheet under cryogenic temperatures for design of liquefied natural gas insulation system. Mater. Des. 2014, 57, 26–39. [Google Scholar] [CrossRef]
- Chen, A.; Wang, C.; Jiang, J.; Ruan, H.; Lu, J. Microstructure Evolution and Mechanical Properties of Austenite Stainless Steel with Gradient Twinned Structure by Surface Mechanical Attrition Treatment. Nanomaterials 2021, 11, 1624. [Google Scholar] [CrossRef]
- Flinn, J.E.; Bae, J.C.; Kelly, T.F.; Korth, G.E. Microstructure stabilization in a rapidly solidified. Metall. Mater. Trans. A 1992, 23, 2557–2565. [Google Scholar] [CrossRef]
- Du Toit, M.; Steyn, H.G. Comparing the formability of AISI 304 and AISI 202 stainless steels. J. Mater. Eng. Perform. 2012, 21, 1491–1495. [Google Scholar] [CrossRef]
- Qu, S.; Huang, C.X.; Gao, Y.L.; Yang, G.; Wu, S.D.; Zang, Q.S.; Zhang, Z.F. Tensile and compressive properties of AISI 304L stainless steel subjected to equal channel angular pressing. Mater. Sci. Eng. A 2008, 475, 207–216. [Google Scholar] [CrossRef]
- Huang, C.X.; Yang, G.; Gao, Y.L.; Wu, S.D.; Zhang, Z.F. Influence of processing temperature on the microstructures and tensile properties of 304L stainless steel by ECAP. Mater. Sci. Eng. A 2008, 485, 643–650. [Google Scholar] [CrossRef]
- Zheng, Z.J.; Gao, Y.; Gui, Y.; Zhu, M. Optimization of strength and ductility in ultra-fine 304 stainless steel after equal-channel angular processing. Mater. Sci. Forum 2011, 667–669, 937–942. [Google Scholar] [CrossRef]
- Milad, M.; Zreiba, N.; Elhalouani, F.; Baradai, C. The Effect of cold work on structure and properties of AISI 304 stainless steel. J. Mater. Process. Technol. 2008, 203, 80–85. [Google Scholar] [CrossRef]
- Schino, A.D.; Salvatori, I.; Kenny, J.M. Effects of martensite formation and austenite reversion on grain refining of AISI 304 stainless steel. J. Mater. Sci. 2002, 37, 4561–4565. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, M.; Yuan, F.; Wu, X. A review on heterogeneous nanostructures: A strategy for superior mechanical properties in metals. Metals 2019, 9, 598. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Zhu, Y.; Lu, K. Ductility and strain hardening in gradient and lamellar structured materials. Scr. Mater. 2020, 186, 321–325. [Google Scholar] [CrossRef]
- Yang, M.; Pan, Y.; Yuan, F.; Zhu, Y.; Wu, X. Back stress strengthening and strain hardening in gradient structure. Mater. Res. Lett. 2016, 4, 145–151. [Google Scholar] [CrossRef]
- Huang, G.L.; Matlock, D.K.; Krauss, G. Martensite formation, strain rate sensitivity, and deformation behavior of type 304 stainless steel sheet. Metall. Trans. A 1989, 20, 1239–1246. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, S.; Yang, M.; Yuan, F.; Wu, X. Simultaneous Improvement of Yield Strength and Ductility at Cryogenic Temperature by Gradient Structure in 304 Stainless Steel. Nanomaterials 2021, 11, 1856. https://doi.org/10.3390/nano11071856
Qin S, Yang M, Yuan F, Wu X. Simultaneous Improvement of Yield Strength and Ductility at Cryogenic Temperature by Gradient Structure in 304 Stainless Steel. Nanomaterials. 2021; 11(7):1856. https://doi.org/10.3390/nano11071856
Chicago/Turabian StyleQin, Shuang, Muxin Yang, Fuping Yuan, and Xiaolei Wu. 2021. "Simultaneous Improvement of Yield Strength and Ductility at Cryogenic Temperature by Gradient Structure in 304 Stainless Steel" Nanomaterials 11, no. 7: 1856. https://doi.org/10.3390/nano11071856
APA StyleQin, S., Yang, M., Yuan, F., & Wu, X. (2021). Simultaneous Improvement of Yield Strength and Ductility at Cryogenic Temperature by Gradient Structure in 304 Stainless Steel. Nanomaterials, 11(7), 1856. https://doi.org/10.3390/nano11071856