Determining the Preferred Orientation of Silver-Plating via X-ray Diffraction Profile
Abstract
:1. Introduction
2. Experimental and Rietveld Calculations
2.1. Materials Preparation, Electroplating
2.2. X-ray Diffraction Profile and Texture Measurement
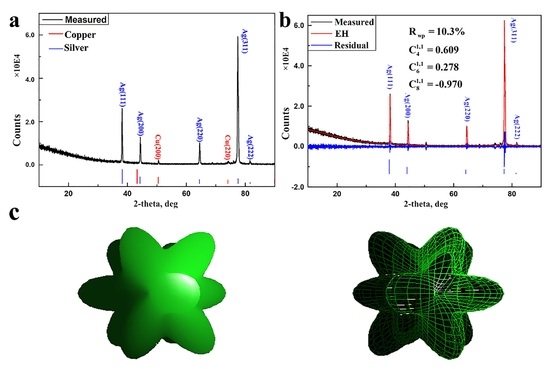
2.3. Rietveld Analysis of X-ray Diffraction Profile
2.3.1. Terminology and Definition of Texture and Preferred Orientation
2.3.2. Initial Rietveld Refinements Assuming No Preferred Orientation
2.3.3. Rietveld Method with Quantitative Texture Analysis (RM+QTA)
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Badini, C.; Padovano, E.; Camillus, R.D.; Lambertini, V.G.; Pietroluongo, M. Oriented structure of short fiber reinforced polymer composites processed by selective laser sintering: The role of powder-spreading process. J. Appl. Polym. Sci. 2020, 137, 49152. [Google Scholar] [CrossRef]
- Ryu, K.R.; Dong, H.N.; Lee, S.; Ha, J.W. Influence of the Preferred Orientation of Pyridine Derivatives with Donor Substituents on Chemical Interface Damping Induced in Silver-Coated Gold Nanorods with Different Shell Thicknesses. J. Phys. Chem. C 2020, 124, 14818. [Google Scholar] [CrossRef]
- Li, F.K.; Liu, Z.B.; Shen, J.D.; Xu, X.J.; Li, Y.; Zhang, D.D.; Zuo, S.Y.; Liu, J. Ni-Rich Layered Oxide with Preferred Orientation (110) Plane as a Stable Cathode Material for High-Energy Lithium-Ion Batteries. J. Nanomater. 2020, 10, 2495. [Google Scholar] [CrossRef] [PubMed]
- Rehman, A.; Arepalli, D.; Alam, S.F.; Kim, M.Z.; Choi, J.; Cho, C.H. Two-Dimensional MFI Zeolite Nanosheets Exfoliated by Surfactant Assisted Solution Process. Nanomaterials 2021, 11, 2327. [Google Scholar] [CrossRef]
- Li, W.; Hao, J.; Liu, W.; Mu, S. Electrodeposition of nano Ni–Co alloy with (220) preferred orientation from choline chloride-urea: Electrochemical behavior and nucleation mechanism. J. Alloys Compd. 2021, 853, 157158. [Google Scholar] [CrossRef]
- Li, T.T.; Dang, N.; Liang, M.M.; Guo, C.L.; Lu, H.H.; Ma, J.Y.; Liang, W. TEM observation of general growth behavior for silver electroplating on copper rod. Appl. Surf. Sci. 2018, 451, 148. [Google Scholar] [CrossRef]
- Sitepu, H.; O’Connor, B.H.; Li, D. Comparative evaluation of the March and generalized spherical harmonic preferred orientation models using X-ray diffraction data for molybdite and calcite powders. J. Appl. Crystallogr. 2005, 38, 158. [Google Scholar] [CrossRef]
- Matthies, S.; Lutteroti, L.; Wenk, H.R. Combined texture and structure analysis of deformed limestone from time-of-flight neutron diffraction spectra. J. Appl. Crystallogr. 1997, 30, 31. [Google Scholar] [CrossRef]
- Jung, Y.S. Study on texture evolution and properties of silver thin films prepared by sputtering deposition. Appl. Surf. Sci. 2004, 221, 281. [Google Scholar] [CrossRef]
- Zoo, Y.; Alford, T.L. Comparison of preferred orientation and stress in silver thin films on different substrates using X-ray diffraction. J. Appl. Phys. 2007, 101, 4287. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65. [Google Scholar] [CrossRef]
- Ferrari, M.; Lutterotti, L.J. Method for the Simultaneous Determination of Anisotropic Residual Stresses and Texture by X-Ray Diffraction. Appl. Phys. 1994, 76, 7246. [Google Scholar] [CrossRef]
- Ferrari, M.; Lutterotti, L.; Matthies, S.; Polonioli, P.; Wenk, H.P. New opportunities in the texture and stress field by the whole pattern analysis. Mater. Sci. Forum 1996, 83, 228. [Google Scholar]
- Lutterotti, L.; Gialanella, S. X-ray diffraction characterization of heavily deformed metallic specimens. Acta Mater. 1998, 46, 101. [Google Scholar] [CrossRef]
- Lutterotti, L.; Polonioli, P.; Orsini, P.G.; Ferrari, M. Stress and texture analysis of zirconia coatings by XRD total pattern fitting. ASME-Mater. Des. Technol. 1994, 62, 15. [Google Scholar]
- Wenk, H.R.; Matthies, S.; Lutterotti, L. Texture Analysis from Diffraction Spectra. Mater. Sci. Forum 1994, 473, 157–162. [Google Scholar]
- Bunge, H.J. Texture Analysis in Material Science. In Mathematical Methods; Butterworth & Co.: Oxford, UK, 1982; pp. 1–5. [Google Scholar]
- Dollase, W.A. Correction of Intensities for Preferred Orientation in Powder Diffractometry: Application of the March Model. J. Appl. Crystallogr. 1986, 19, 267. [Google Scholar] [CrossRef]
- Li, T.; Dang, N.; Zhang, W.; Liang, W.; Yang, F.Q. Determining the Degree of [001] Preferred Growth of Ni(OH)2 Nanoplates. Nanomaterials 2018, 8, 991. [Google Scholar] [CrossRef] [Green Version]
- Zolotoyabko, E.J. Determination of the degree of preferred orientation within the March–Dollase approach. Appl. Crystallogr. 2010, 42, 513. [Google Scholar] [CrossRef]
- Bail, A.L.; Duroy, H.; Fourquet, J.L. Ab Initio Structure Determination of LiSbWO6 by X-ray Powder Diffraction. Mater. Res. Bull. 1988, 23, 447. [Google Scholar] [CrossRef]
- Chateigner, D. Combined Analysis; Wiley-ISTE: London, UK, 2010; pp. 146–162. [Google Scholar]
- Popa, N.C.; Balzar, D.J. An analytical approximation for a size-broadened profile given by the lognormal and gamma distributions. Appl. Crystallogr. 2002, 35, 338. [Google Scholar] [CrossRef] [Green Version]
- Thompson, C.V. On the grain size and coalescence stress resulting from nucleation and growth processes during formation of polycrystalline thin films. J. Mater. Res. 1999, 14, 3164. [Google Scholar] [CrossRef]



| Instrument | Smartlab |
|---|---|
| Radiation | Cu anode tube operated at 40 kV and 30 mA Wavelength: Cu Kα = 1.5418 Å, Cu Kα1 = 1.54060 Å, Cu Kα2 = 1.54441 Å |
| Optics | Parallel beam (PB) |
| Specimen | Flatted sample |
| Detection | Name: DteX250 (H); Pixel sizes: 0.075 |
| Scan speed | 20°/min |
| Sollerslit | 2.5 deg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Zheng, L.; Zhang, W.; Zhu, P. Determining the Preferred Orientation of Silver-Plating via X-ray Diffraction Profile. Nanomaterials 2021, 11, 2417. https://doi.org/10.3390/nano11092417
Li T, Zheng L, Zhang W, Zhu P. Determining the Preferred Orientation of Silver-Plating via X-ray Diffraction Profile. Nanomaterials. 2021; 11(9):2417. https://doi.org/10.3390/nano11092417
Chicago/Turabian StyleLi, Taotao, Liuwei Zheng, Wanggang Zhang, and Pengfei Zhu. 2021. "Determining the Preferred Orientation of Silver-Plating via X-ray Diffraction Profile" Nanomaterials 11, no. 9: 2417. https://doi.org/10.3390/nano11092417
APA StyleLi, T., Zheng, L., Zhang, W., & Zhu, P. (2021). Determining the Preferred Orientation of Silver-Plating via X-ray Diffraction Profile. Nanomaterials, 11(9), 2417. https://doi.org/10.3390/nano11092417