Simulating and Predicting Adsorption of Organic Pollutants onto Black Phosphorus Nanomaterials
Abstract
:1. Introduction
2. Computational Methods
2.1. DFT Calculation
2.2. MD Simulation
2.3. pp-LFER Modeling
3. Results and Discussion
3.1. Reliability of Computational Methods
3.2. G(Z) and Ead of the Adsorbates onto BP
3.3. Adsorption Configurations
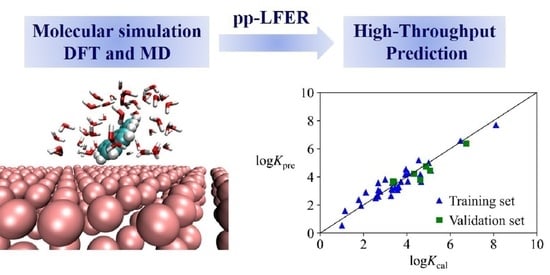
3.4. pp-LFER Models
ntra = 33, R2adj = 0.96, RMSEtra = 0.35, Q2LOO = 0.95, Q2kfold (k = 5, 5000) = 0.95,
next = 8, RMSEext = 0.35, Q2ext = 0.97
ntra = 33, R2adj = 0.87, RMSEtra = 0.46, Q2LOO = 0.83, Q2kfold (k = 5, 5000) = 0.82,
next = 8, RMSEext = 0.43, Q2ext = 0.90
ntra = 33, R2adj = 0.97, RMSEtra = 0.62, Q2LOO = 0.96, Q2kfold (k = 5, 5000) = 0.96,
next = 8, RMSEext = 0.61, Q2ext = 0.97
ntra = 33, R2adj = 0.96, RMSEtra = 0.66, Q2LOO = 0.95, Q2kfold (k = 5, 5000) = 0.94,
next = 8, RMSEext = 0.73, Q2ext = 0.96
3.5. Comparisons with Graphene
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qiu, M.; Ren, W.X.; Jeong, T.; Won, M.; Park, G.Y.; Sang, D.K.; Liu, L.P.; Zhang, H.; Kim, J.S. Omnipotent phosphorene: A next-generation, two-dimensional nanoplatform for multidisciplinary biomedical applications. Chem. Soc. Rev. 2018, 47, 5588–5601. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.W.; Hu, K.; Yan, D.F.; Chen, R.; Zou, Y.Q.; Liu, H.B.; Wang, S.Y. Recent Advances on Black Phosphorus for Energy Storage, Catalysis, and Sensor Applications. Adv. Mater. 2018, 30, 1800295. [Google Scholar] [CrossRef]
- Ling, X.; Wang, H.; Huang, S.X.; Xia, F.N.; Dresselhaus, M.S. The renaissance of black phosphorus. Proc. Natl. Acad. Sci. USA 2015, 112, 4523–4530. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carvalho, A.; Wang, M.; Zhu, X.; Rodin, A.S.; Su, H.B.; Neto, A.H.C. Phosphorene: From theory to applications. Nat. Rev. Mater. 2016, 1, 16061. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, T.L.; Xiao, L.G.; Kolaczkowski, M.A.; Zhang, L.; Klivansky, L.M.; Altoe, V.; Tian, B.; Guo, J.H.; Peng, X.B.; et al. Facile integration of low-cost black phosphorus in solution-processed organic solar cells with improved fill factor and device efficiency. Nano Energy 2018, 53, 345–353. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Ma, W.; Pan, B.; Zhang, Q.R.; Zhang, X.J.; Zhang, S.Y.; Xing, B.S. Wrinkle-induced high sorption makes few-layered black phosphorus a superior adsorbent for ionic organic compounds. Environ. Sci. Nano 2018, 5, 1454–1465. [Google Scholar] [CrossRef]
- Chen, W.S.; Ouyang, J.; Liu, H.; Chen, M.; Zeng, K.; Sheng, J.P.; Liu, Z.J.; Han, Y.J.; Wang, L.Q.; Li, J.; et al. Black Phosphorus Nanosheet-Based Drug Delivery System for Synergistic Photodynamic/Photothermal/Chemotherapy of Cancer. Adv. Mater. 2017, 29, 1603864. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Yao, L.L.; Zhao, X.C.; Zeng, L.; Li, P.; Yang, X.X.; Zhang, L.; Cai, Z.W.; Shi, J.B.; Qu, G.B.; et al. Cellular Uptake of Few-Layered Black Phosphorus and the Toxicity to an Aquatic Unicellular Organism. Environ. Sci. Technol. 2020, 54, 1583–1592. [Google Scholar] [CrossRef]
- Qu, G.B.; Xia, T.; Zhou, W.H.; Zhang, X.; Zhang, H.Y.; Hu, L.G.; Shi, J.B.; Yu, X.F.; Jiang, G.B. Property-Activity Relationship of Black Phosphorus at the Nano-Bio Interface: From Molecules to Organisms. Chem. Rev. 2020, 120, 2288–2346. [Google Scholar] [CrossRef]
- Li, P.; Zeng, L.; Gao, J.; Yao, L.L.; Zhao, X.C.; Wu, Q.; Liu, X.L.; Wang, Y.Y.; Yang, X.X.; Shi, J.B.; et al. Perturbation of Normal Algal Growth by Black Phosphorus Nanosheets: The Role of Degradation. Environ. Sci. Technol. Lett. 2020, 7, 35–41. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, Z.Y.; White, J.C.; Xing, B.S. Graphene in the Aquatic Environment: Adsorption, Dispersion, Toxicity and Transformation. Environ. Sci. Technol. 2014, 48, 9995–10009. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Xing, B.S. Adsorption of Organic Compounds by Carbon Nanomaterials in Aqueous Phase: Polanyi Theory and Its Application. Chem. Rev. 2010, 110, 5989–6008. [Google Scholar] [CrossRef] [PubMed]
- Glomstad, B.; Altin, D.; Sorensen, L.; Liu, J.F.; Jenssen, B.M.; Booth, A.M. Carbon Nanotube Properties Influence Adsorption of Phenanthrene and Subsequent Bioavailability and Toxicity to Pseudokirchneriella subcapitata. Environ. Sci. Technol. 2016, 50, 2660–2668. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, T.M.; Wan, Y.Y.; Xie, H.Y.; Mu, Y.; Du, P.W.; Wang, D.; Wu, X.J.; Ji, H.X.; Wan, L.J. Degradation Chemistry and Stabilization of Exfoliated Few-Layer Black Phosphorus in Water. J. Am. Chem. Soc. 2018, 140, 7561–7567. [Google Scholar] [CrossRef]
- Ersan, G.; Apul, O.G.; Perreault, F.; Karanfil, T. Adsorption of organic contaminants by graphene nanosheets: A review. Water Res. 2017, 126, 385–398. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.W.; Wei, X.X.; Maldonado, A.J.H.; Chen, Z.F. Unveiling Adsorption Mechanisms of Organic Pollutants onto Carbon Nanomaterials by Density Functional Theory Computations and Linear Free Energy Relationship Modeling. Environ. Sci. Technol. 2017, 51, 11820–11828. [Google Scholar] [CrossRef]
- Apul, O.G.; Wang, Q.L.; Shao, T.; Rieck, J.R.; Karanfil, T. Predictive model development for adsorption of aromatic contaminants by multi-walled carbon nanotubes. Environ. Sci. Technol. 2013, 47, 2295–2303. [Google Scholar] [CrossRef] [PubMed]
- Huffer, T.; Endo, S.; Metzelder, F.; Schroth, S.; Schmidt, T.C. Prediction of sorption of aromatic and aliphatic organic compounds by carbon nanotubes using poly-parameter linear free-energy relationships. Water Res. 2014, 59, 295–303. [Google Scholar] [CrossRef]
- Ersan, G.; Apul, O.G.; Karanfil, T. Linear solvation energy relationships (LSER) for adsorption of organic compounds by carbon nanotubes. Water Res. 2016, 98, 28–38. [Google Scholar] [CrossRef] [Green Version]
- Ersan, G.; Apul, O.G.; Karanfil, T. Predictive models for adsorption of organic compounds by Graphene nanosheets: Comparison with carbon nanotubes. Sci. Total Environ. 2019, 654, 28–34. [Google Scholar] [CrossRef]
- Chen, X.X.; Chen, B.L. Macroscopic and Spectroscopic Investigations of the Adsorption of Nitroaromatic Compounds on Graphene Oxide, Reduced Graphene Oxide, and Graphene Nanosheets. Environ. Sci. Technol. 2015, 49, 6181–6189. [Google Scholar] [CrossRef]
- Yu, S.J.; Wang, X.X.; Yao, W.; Wang, J.; Ji, Y.F.; Ai, Y.J.; Alsaedi, A.; Hayat, T.; Wang, X.K. Macroscopic, Spectroscopic, and Theoretical Investigation for the Interaction of Phenol and Naphthol on Reduced Graphene Oxide. Environ. Sci. Technol. 2017, 51, 3278–3286. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.X.; Wang, X.X.; Sun, Y.B.; Ai, Y.J.; Wang, X.K. Adsorption of 4-n-Nonylphenol and Bisphenol-A on Magnetic Reduced Graphene Oxides: A Combined Experimental and Theoretical Studies. Environ. Sci. Technol. 2015, 49, 9168–9175. [Google Scholar] [CrossRef] [PubMed]
- Lazar, P.; Karlicky, F.; Jurecka, P.; Kocman, M.; Otyepkova, E.; Safarova, K.; Otyepka, M. Adsorption of Small Organic Molecules on Graphene. J. Am. Chem. Soc. 2013, 135, 6372–6377. [Google Scholar] [CrossRef]
- Zou, M.Y.; Zhang, J.D.; Chen, J.W.; Li, X.H. Simulating Adsorption of Organic Pollutants on Finite (8,0) Single-Walled Carbon Nanotubes in Water. Environ. Sci. Technol. 2012, 46, 8887–8894. [Google Scholar] [CrossRef] [PubMed]
- Azhagiya-Singam, E.R.; Zhang, Y.; Magnin, G.; Miranda-Carvajal, I.; Coates, L.; Thakkar, R.; Poblete, H.; Comer, J. Thermodynamics of Adsorption on Graphenic Surfaces from Aqueous Solution. J. Chem. Theory Comput. 2019, 15, 1302–1316. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Duan, L.; Zhu, D.Q. Adsorption of polar and nonpolar organic chemicals to carbon nanotubes. Environ. Sci. Technol. 2007, 41, 8295–8300. [Google Scholar] [CrossRef] [PubMed]
- Lazar, P.; Otyepkova, E.; Pykal, M.; Cepe, K.; Otyepka, M. Role of the puckered anisotropic surface in the surface and adsorption properties of black phosphorus. Nanoscale 2018, 10, 8979–8988. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Comer, J.; Chen, Z.F.; Chen, J.W.; Gumbart, J.C. Exploring adsorption of neutral aromatic pollutants onto graphene nanomaterials via molecular dynamics simulations and theoretical linear solvation energy relationships. Environ. Sci. Nano 2018, 5, 2117–2128. [Google Scholar] [CrossRef]
- Comer, J.; Chen, R.; Poblete, H.; Vergara-Jaque, A.; Riviere, J.E. Predicting adsorption affinities of small molecules on carbon nanotubes using molecular dynamics simulation. Acs Nano 2015, 9, 11761–11774. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zuo, L.Z.; Guo, Y.; Li, X.; Fu, H.Y.; Qu, X.L.; Zheng, S.R.; Gu, C.; Zhu, D.Q.; Alvarez, P.J.J. Enhanced Adsorption of Hydroxyl- and Amino-Substituted Aromatic Chemicals to Nitrogen-Doped Multiwall Carbon Nanotubes: A Combined Batch and Theoretical Calculation Study. Environ. Sci. Technol. 2016, 50, 899–905. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Zhao, Y.; Shan, S.J.; Yang, X.N.; Liu, D.M.; Cui, F.Y.; Xing, B.S. Wrinkle- and edge-adsorption of aromatic compounds on graphene oxide as revealed by atomic force microscopy, molecular dynamics simulation, and density functional theory. Environ. Sci. Technol. 2018, 52, 7689–7697. [Google Scholar] [CrossRef] [PubMed]
- Endo, S.; Goss, K.U. Applications of Polyparameter Linear Free Energy Relationships in Environmental Chemistry. Environ. Sci. Technol. 2014, 48, 12477–12491. [Google Scholar] [CrossRef]
- Ding, H.; Chen, C.; Zhang, X. Linear solvation energy relationship for the adsorption of synthetic organic compounds on single-walled carbon nanotubes in water. SAR QSAR Environ. Res. 2016, 27, 31–45. [Google Scholar] [CrossRef] [PubMed]
- Rubio-Pereda, P.; Cocoletzi, G.H. Density functional theory calculations of biomolecules adsorption on phosphorene for biomedical applications. Appl. Surf. Sci. 2018, 427, 1227–1234. [Google Scholar] [CrossRef]
- Zhang, H.P.; Hou, J.L.; Wang, Y.B.; Tang, P.P.; Zhang, Y.P.; Lin, X.Y.; Liu, C.S.; Tang, Y.H. Adsorption behavior of 2, 3, 7, 8-tetrachlorodibenzo-p-dioxin on pristine and doped black phosphorene: A DFT study. Chemosphere 2017, 185, 509–517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delley, B. From molecules to solids with the dmol3 approach. J. Chem. Phys. 2000, 113, 7756–7764. [Google Scholar] [CrossRef]
- Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 1990, 92, 508–517. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Chen, X.F.; Jia, S.L.; Ding, N.; Shi, J.B.; Wang, Z.H. Capture of aromatic organic pollutants by hexagonal boron nitride nanosheets: Density functional theoretical and molecular dynamic investigation. Environ. Sci. Nano 2016, 3, 1493–1503. [Google Scholar] [CrossRef]
- Benedek, N.A.; Snook, I.K.; Latham, K.; Yarovsky, I. Application of numerical basis sets to hydrogen bonded systems: A density functional theory study. J. Chem. Phys. 2005, 122, 144102. [Google Scholar] [CrossRef] [PubMed]
- Inada, Y.; Orita, H. Efficiency of numerical basis sets for predicting the binding energies of hydrogen bonded complexes: Evidence of small basis set superposition error compared to Gaussian basis sets. J. Comput. Chem. 2008, 29, 225–232. [Google Scholar] [CrossRef] [PubMed]
- Delley, B. Hardness conserving semilocal pseudopotentials. Phys. Rev. B 2002, 66, 155125. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points For Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Andzelm, J.; Kölmel, C.; Klamt, A. Incorporation of solvent effects into density functional calculations of molecular energies and geometries. J. Chem. Phys. 1995, 103, 9312–9320. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef] [Green Version]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [Green Version]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM General Force Field: A Force Field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [Green Version]
- Vanommeslaeghe, K.; MacKerell, A.D. Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell, A.D. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mayne, C.G.; Saam, J.; Schulten, K.; Tajkhorshid, E.; Gumbart, J.C. Rapid Parameterization of Small Molecules Using the Force Field Toolkit. J. Comput. Chem. 2013, 34, 2757–2770. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sreshtt, V.; Padua, A.A.H.; Blankschtein, D. Liquid-Phase Exfoliation of Phosphorene: Design Rules from Molecular Dynamics Simulations. Acs Nano 2015, 9, 8255–8268. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.H.; Pastor, R.W.; Brooks, B.R. Constant pressure molecular dynamics simulations: The Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log N method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Darve, E.; Pohorille, A. Calculating free energies using average force. J. Chem. Phys. 2001, 115, 9169–9183. [Google Scholar] [CrossRef] [Green Version]
- Comer, J.; Gumbart, J.C.; Henin, J.; Lelievre, T.; Pohorille, A.; Chipot, C. The adaptive biasing force method: Everything you always wanted to know, but were afraid to ask. J. Phys. Chem. B 2015, 119, 1129–1151. [Google Scholar] [CrossRef] [Green Version]
- Fiorin, G.; Klein, M.L.; Henin, J. Using collective variables to drive molecular dynamics simulations. Mol. Phys. 2013, 111, 3345–3362. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Peigney, A.; Laurent, C.; Flahaut, E.; Bacsa, R.R.; Rousset, A. Specific surface area of carbon nanotubes and bundles of carbon nanotubes. Carbon 2001, 39, 507–514. [Google Scholar] [CrossRef] [Green Version]
- Ulrich, N.; Endo, S.; Brown, T.N.; Watanabe, N.; Bronner, G.; Abraham, M.H.; Goss, K.U. UFZ-LSER Database v 3.2 [Internet]. 2017. Available online: http://www.ufz.de/lserd (accessed on 20 December 2021).
- OECD. Guidance Document on the Validation of (Quantitative) Structure-Activity Relationship [(Q)SAR] Models; OECD: Paris, France, 2007. [Google Scholar] [CrossRef]
- Gramatica, P. Principles of QSAR models validation: Internal and external. QSAR Comb. Sci. 2007, 26, 694–701. [Google Scholar] [CrossRef]
- Otyepkova, E.; Lazar, P.; Cepe, K.; Tomanec, O.; Otyepka, M. Organic adsorbates have higher affinities to fluorographene than to graphene. Appl. Mater. Today 2016, 5, 142–149. [Google Scholar] [CrossRef] [Green Version]
- Goss, K.U.; Schwarzenbach, R.P. Linear free energy relationships used to evaluate equilibrium partitioning of organic compounds. Environ. Sci. Technol. 2001, 35, 1–9. [Google Scholar] [CrossRef]
- Saeedimasine, M.; Brandt, E.G.; Lyubartsev, A.P. Atomistic Perspective on Biomolecular Adsorption on Functionalized Carbon Nanomaterials under Ambient Conditions. J. Phys. Chem. B 2021, 125, 416–430. [Google Scholar] [CrossRef]
- Zhao, D.; Peng, C.; Zhou, J. Lipase adsorption on different nanomaterials: A multi-scale simulation study. Phys. Chem. Chem. Phys. 2015, 17, 840–850. [Google Scholar] [CrossRef]
- Cortes-Arriagada, D. Phosphorene as a template material for physisorption of DNA/RNA nucleobases and resembling of base pairs: A cluster DFT sudy and comparisons with graphene. J. Phys. Chem. C 2018, 122, 4870–4880. [Google Scholar] [CrossRef]
- Wang, J.; Chen, B.; Xing, B. Wrinkles and Folds of Activated Graphene Nanosheets as Fast and Efficient Adsorptive Sites for Hydrophobic Organic Contaminants. Environ. Sci. Technol. 2016, 50, 3798–3808. [Google Scholar] [CrossRef]
- Golbraikh, A.; Shen, M.; Xiao, Z.Y.; Xiao, Y.D.; Lee, K.H.; Tropsha, A. Rational selection of training and test sets for the development of validated QSAR models. J. Comput.-Aided Mol. Des. 2003, 17, 241–253. [Google Scholar] [CrossRef]
- Shen, X.E.; Shan, X.Q.; Dong, D.M.; Hua, X.Y.; Owens, G. Kinetics and thermodynamics of sorption of nitroaromatic compounds to as-grown and oxidized multiwalled carbon nanotubes. J. Colloid Interface Sci. 2009, 330, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Shan, S.; Zhao, Y.; Tang, H.; Cui, F. Linear solvation energy relationship to predict the adsorption of aromatic contaminants on graphene oxide. Chemosphere 2017, 185, 826–832. [Google Scholar] [CrossRef] [PubMed]
- Xia, X.R.; Monteiro-Riviere, N.A.; Riviere, J.E. An index for characterization of nanomaterials in biological systems. Nat. Nanotechnol. 2010, 5, 671–675. [Google Scholar] [CrossRef] [PubMed]




| Term | |Ead| | logK | a logK | b logK | ||
|---|---|---|---|---|---|---|
| TΔS | |Ead| | ΔGH2O | ΔGMD (Gaseous) | |||
| eE | 23% | 17% | −47% | 62% | −5% | 21% |
| sS | −26% | 20% | 93% | −70% | −8% | 30% |
| aA | 1% | 0 | −3% | 3% | 2% | −2% |
| bB | 3% | −1% | −11% | 9% | −1% | −1% |
| vV | 88% | 111% | −126% | 239% | −49% | 162% |
| c Sum | 89% | 147% | −94% | 243% | −61% | 210% |
| No. | Nanomaterial | Phase | Ntrain | R2train | Prediction Model |
|---|---|---|---|---|---|
| 1 | SWCNT [34] | aqueous | 30 | 0.87 | logK = −1.3 + 0.40E + 0.36S + 0.93A − 3.9B + 2.8V |
| 2 | MWCNT [17] | aqueous | 29 | 0.83 | logK = −4.3 + 0.61S + 0.050A − 0.48B + 4.5V |
| 3 | MWCNT [75] | aqueous | 28 | 0.93 | logK = −1.3 + 0.043E + 1.7S − 0.37A − 2.7B + 4.1V |
| 4 | Graphene [20] | aqueous | 29 | 0.89 | logK = −1.4 + 0.11E + 1.4S + 0.42A − 3.8B + 2.2V |
| 5 | Graphene [29] | aqueous | 35 | 0.88 | logK = −1.8εα − 1.2εβ + 1.3q+ − 1.5q− + 1.0V − 1.6π + 42 |
| 6 | Graphene oxide [20] | aqueous | 36 | 0.84 | logK = −1.4 + 0.29E + 0.28S − 0.19A − 2.6B + 2.6V |
| 7 | Graphene oxide [74] | aqueous | 36 | 0.92 | logK = −1.7 + 0.93E + 0.060S − 0.38A − 1.9B + 2.2V |
| 8 | BP (this study) | aqueous | 33 | 0.87 | logK = −1.7 + 0.65E + 0.75S + 0.048A – 0.095B + 4.0V |
| 9 | BP (this study) | gaseous | 33 | 0.96 | logK = 0.2 − 0.0076E − 1.1S − 1.1A + 1.4B + 1.5L |
| 10 | Graphene (this study) | aqueous | 30 | 0.86 | logK = −1.6 + 0.42E + 1.0S + 0.26A − 0.78B + 4.0V |
| 11 | Graphene (this study) | gaseous | 30 | 0.97 | logK = 0.052 − 0.043E − 0.62S − 0.78A − 0.36B + 1.5L |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, L.; Wang, Y.; Wang, Z.; Zhang, S.; Xiao, Z.; Xia, D.; Chen, J. Simulating and Predicting Adsorption of Organic Pollutants onto Black Phosphorus Nanomaterials. Nanomaterials 2022, 12, 590. https://doi.org/10.3390/nano12040590
Su L, Wang Y, Wang Z, Zhang S, Xiao Z, Xia D, Chen J. Simulating and Predicting Adsorption of Organic Pollutants onto Black Phosphorus Nanomaterials. Nanomaterials. 2022; 12(4):590. https://doi.org/10.3390/nano12040590
Chicago/Turabian StyleSu, Lihao, Ya Wang, Zhongyu Wang, Siyu Zhang, Zijun Xiao, Deming Xia, and Jingwen Chen. 2022. "Simulating and Predicting Adsorption of Organic Pollutants onto Black Phosphorus Nanomaterials" Nanomaterials 12, no. 4: 590. https://doi.org/10.3390/nano12040590
APA StyleSu, L., Wang, Y., Wang, Z., Zhang, S., Xiao, Z., Xia, D., & Chen, J. (2022). Simulating and Predicting Adsorption of Organic Pollutants onto Black Phosphorus Nanomaterials. Nanomaterials, 12(4), 590. https://doi.org/10.3390/nano12040590