Understanding the Morphological Evolution of InSb Nanoflags Synthesized in Regular Arrays by Chemical Beam Epitaxy
Abstract
:1. Introduction
2. Materials and Methods
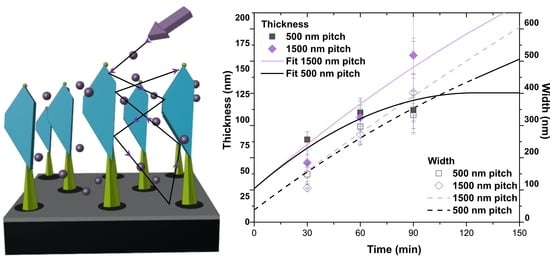
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ashley, T.; Dean, A.B.; Elliott, C.T.; Pryce, G.J.; Johnson, A.D.; Willis, H. Uncooled high-speed InSb field-effect transistors. Appl. Phys. Lett. 1995, 66, 481–483. [Google Scholar] [CrossRef]
- Žutić, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef] [Green Version]
- Chochol, J.; Postava, K.; Čada, M.; Pištora, J. Experimental demonstration of magnetoplasmon polariton at InSb(InAs)/dielectric interface for terahertz sensor application. Sci. Rep. 2017, 7, 13117. [Google Scholar] [CrossRef] [PubMed]
- Qu, F.; Van Veen, J.; De Vries, F.K.; Beukman, A.J.A.; Wimmer, M.T.; Yi, W.; Kiselev, A.A.; Nguyen, B.-M.; Sokolich, M.; Manfra, M.J.; et al. Quantized Conductance and Large g-Factor Anisotropy in InSb Quantum Point Contacts. Nano Lett. 2016, 16, 7509–7513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Z.; Heischmidt, B.; Gazibegovic, S.; Badawy, G.; Car, D.; Crowell, P.A.; Bakkers, E.P.; Pribiag, V.S. Spin Transport in Ferromagnet-InSb Nanowire Quantum Devices. Nano Lett. 2020, 20, 3232–3239. [Google Scholar] [CrossRef]
- Nowack, K.C.; Koppens, F.H.L.; Nazarov, Y.V.; Vandersypen, L.M.K. Coherent Control of a Single Electron Spin with Electric Fields. Science 2007, 318, 1430–1433. [Google Scholar] [CrossRef] [Green Version]
- Berg, J.W.G.V.D.; Nadj-Perge, S.; Pribiag, V.S.; Plissard, S.; Bakkers, E.P.A.M.; Frolov, S.M.; Kouwenhoven, L.P. Fast Spin-Orbit Qubit in an Indium Antimonide Nanowire. Phys. Rev. Lett. 2013, 110, 066806. [Google Scholar] [CrossRef] [Green Version]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083–1159. [Google Scholar] [CrossRef] [Green Version]
- Moehle, C.M.; Ke, C.T.; Wang, Q.; Thomas, C.; Xiao, D.; Karwal, S.; Lodari, M.; van de Kerkhof, V.; Termaat, R.; Gardner, G.C.; et al. InSbAs Two-Dimensional Electron Gases as a Platform for Topological Superconductivity. Nano Lett. 2021, 21, 9990–9996. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, S.; Mu, J.; Pan, D.; Zhao, J.; Xu, H.-Q. A double quantum dot defined by top gates in a single crystalline InSb nanosheet. Chin. Phys. B 2021, 30, 128501. [Google Scholar] [CrossRef]
- de la Mata, M.; Leturcq, R.; Plissard, S.R.; Rolland, C.; Magén, C.; Arbiol, J.; Caroff, P. Twin-Induced InSb Nanosails: A Convenient High Mobility Quantum System. Nano Lett. 2016, 16, 825–833. [Google Scholar] [CrossRef] [PubMed]
- Sladek, R.J. Effective Masses of Electrons in Indium Arsenide and Indium Antimonide. Phys. Rev. 1957, 105, 460–464. [Google Scholar] [CrossRef]
- Ke, C.T.; Moehle, C.M.; De Vries, F.K.; Thomas, C.; Metti, S.; Guinn, C.R.; Kallaher, R.; Lodari, M.; Scappucci, G.; Wang, T.; et al. Ballistic superconductivity and tunable π-junctions in InSb quantum wells. Nat. Commun. 2019, 10, 3764. [Google Scholar] [CrossRef]
- de Vries, F.K.; Sol, M.L.; Gazibegovic, S.; Veld, R.L.M.O.H.; Balk, S.C.; Car, D.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Shen, J. Crossed Andreev reflection in InSb flake Josephson junctions. Phys. Rev. Res. 2019, 1, 032031. [Google Scholar] [CrossRef] [Green Version]
- Lei, Z.; Lehner, C.A.; Cheah, E.; Mittag, C.; Karalic, M.; Wegscheider, W.; Ensslin, K.; Ihn, T. Gate-defined quantum point contact in an InSb two-dimensional electron gas. Phys. Rev. Res. 2021, 3, 023042. [Google Scholar] [CrossRef]
- Mourik, V.; Zuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Signatures of Majorana Fermions in Hybrid Superconductor-Semiconductor Nanowire Devices. Science 2012, 336, 1003–1007. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gül, Ö.; Zhang, H.; de Vries, F.K.; van Veen, J.; Zuo, K.; Mourik, V.; Conesa-Boj, S.; Nowak, M.P.; van Woerkom, D.J.; Quintero-Pérez, M.; et al. Hard Superconducting Gap in InSb Nanowires. Nano Lett. 2017, 17, 2690–2696. [Google Scholar] [CrossRef]
- Verma, I.; Salimian, S.; Zannier, V.; Heun, S.; Rossi, F.; Ercolani, D.; Beltram, F.; Sorba, L. High-Mobility Free-Standing InSb Nanoflags Grown on InP Nanowire Stems for Quantum Devices. ACS Appl. Nano Mater. 2021, 4, 5825–5833. [Google Scholar] [CrossRef]
- Kang, N.; Fan, D.; Zhi, J.; Pan, D.; Li, S.; Wang, C.; Guo, J.; Zhao, J.; Xu, H. Two-Dimensional Quantum Transport in Free-Standing InSb Nanosheets. Nano Lett. 2019, 19, 561–569. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, S.; Pan, D.; Xue, J.; Zhang, L.; Zhao, J.; Xu, H.Q. Strong and tunable spin–orbit interaction in a single crystalline InSb nanosheet. NPJ 2D Mater. Appl. 2021, 5, 3. [Google Scholar] [CrossRef]
- Salimian, S.; Carrega, M.; Verma, I.; Zannier, V.; Nowak, M.P.; Beltram, F.; Sorba, L.; Heun, S. Gate-controlled supercurrent in ballistic InSb nanoflag Josephson junctions. Appl. Phys. Lett. 2021, 119, 214004. [Google Scholar] [CrossRef]
- Jiang, J.; Wen, Y.; Wang, H.; Yin, L.; Cheng, R.; Liu, C.; Feng, L.; He, J. Recent Advances in 2D Materials for Photodetectors. Adv. Electron. Mater. 2021, 7, 2001125. [Google Scholar] [CrossRef]
- Cirlin, G.E.; Dubrovskii, V.G.; Sibirev, N.V.; Soshnikov, I.P.; Samsonenko, Y.B.; Tonkikh, A.A.; Ustinov, V.M. The diffusion mechanism in the formation of GaAs and AlGaAs nanowhiskers during the process of molecular-beam epitaxy. Semiconductors 2005, 39, 557–564. [Google Scholar] [CrossRef]
- Dubrovskii, V.; Sibirev, N.; Suris, R.; Cirlin, G.; Harmand, J.; Ustinov, V. Diffusion-controlled growth of semiconductor nanowires: Vapor pressure versus high vacuum deposition. Surf. Sci. 2007, 601, 4395–4401. [Google Scholar] [CrossRef]
- Fröberg, L.E.; Seifert, W.; Johansson, J. Diameter-dependent growth rate of InAs nanowires. Phys. Rev. B 2007, 76, 153401. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Sibirev, N.; Cirlin, G.; Soshnikov, I.P.; Chen, W.; Larde, R.; Cadel, E.; Pareige, P.; Xu, T.; Grandidier, B.; et al. Gibbs-Thomson and diffusion-induced contributions to the growth rate of Si, InP, and GaAs nanowires. Phys. Rev. B 2009, 79, 205316. [Google Scholar] [CrossRef]
- Glas, F.; Harmand, J.-C.; Patriarche, G. Why Does Wurtzite Form in Nanowires of III–V Zinc Blende Semiconductors? Phys. Rev. Lett. 2007, 99, 146101. [Google Scholar] [CrossRef] [Green Version]
- Sibirev, N.V.; Tchernycheva, M.; Timofeeva, M.A.; Harmand, J.-C.; Cirlin, G.E.; Dubrovskii, V.G. Influence of shadow effect on the growth and shape of InAs nanowires. J. Appl. Phys. 2012, 111, 104317. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Sibirev, N.; Harmand, J.-C.; Glas, F. Growth kinetics and crystal structure of semiconductor nanowires. Phys. Rev. B 2008, 78, 235301. [Google Scholar] [CrossRef]
- Dubrovskii, V.G.; Sibirev, N.V.; Cirlin, G.E.; Bouravleuv, A.D.; Samsonenko, Y.B.; Dheeraj, D.L.; Zhou, H.L.; Sartel, C.; Harmand, J.C.; Patriarche, G.; et al. Role of nonlinear effects in nanowire growth and crystal phase. Phys. Rev. B 2009, 80, 205305. [Google Scholar] [CrossRef]
- Johansson, J.; Karlsson, L.S.; Dick, K.; Bolinsson, J.; Wacaser, B.; Deppert, K.; Samuelson, L. Effects of Supersaturation on the Crystal Structure of Gold Seeded III–V Nanowires. Cryst. Growth Des. 2009, 9, 766–773. [Google Scholar] [CrossRef]
- Dick, K.; Caroff, P.; Bolinsson, J.; Messing, M.; Johansson, J.; Deppert, K.; Wallenberg, R.; Samuelson, L. Control of III–V nanowire crystal structure by growth parameter tuning. Semicond. Sci. Technol. 2010, 25, 024009. [Google Scholar] [CrossRef]
- Gazibegovic, S.; Badawy, G.; Buckers, T.L.J.; Leubner, P.; Shen, J.; De Vries, F.K.; Koelling, S.; Kouwenhoven, L.P.; Verheijen, M.A.; Bakkers, E.P.A.M. Bottom-Up Grown 2D InSb Nanostructures. Adv. Mater. 2019, 31, e1808181. [Google Scholar] [CrossRef] [PubMed]
- Pan, D.; Fan, D.X.; Kang, N.; Zhi, J.H.; Yu, X.Z.; Xu, H.Q.; Zhao, J.H. Free-Standing Two-Dimensional Single-Crystalline InSb Nanosheets. Nano Lett. 2016, 16, 834–841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verma, I.; Zannier, V.; Rossi, F.; Ercolani, D.; Beltram, F.; Sorba, L. Morphology control of single-crystal InSb nanostructures by tuning the growth parameters. Nanotechnology 2020, 31, 384002. [Google Scholar] [CrossRef]
- Plante, M.C.; LaPierre, R.R. Analytical description of the metal-assisted growth of III–V nanowires: Axial and radial growths. J. Appl. Phys. 2009, 105, 114304. [Google Scholar] [CrossRef]
- Ramdani, M.R.; Harmand, J.-C.; Glas, F.; Patriarche, G.; Travers, L. Arsenic Pathways in Self-Catalyzed Growth of GaAs Nanowires. Cryst. Growth Des. 2012, 13, 91–96. [Google Scholar] [CrossRef]
- Oehler, F.; Cattoni, A.; Scaccabarozzi, A.; Patriarche, G.; Glas, F.; Harmand, J.-C. Measuring and Modeling the Growth Dynamics of Self-Catalyzed GaP Nanowire Arrays. Nano Lett. 2018, 18, 701–708. [Google Scholar] [CrossRef]
- Dubrovskii, V.G. Theory of MBE Growth of Nanowires on Reflecting Substrates. Nanomaterials 2022, 12, 253. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, I.; Zannier, V.; Dubrovskii, V.G.; Beltram, F.; Sorba, L. Understanding the Morphological Evolution of InSb Nanoflags Synthesized in Regular Arrays by Chemical Beam Epitaxy. Nanomaterials 2022, 12, 1090. https://doi.org/10.3390/nano12071090
Verma I, Zannier V, Dubrovskii VG, Beltram F, Sorba L. Understanding the Morphological Evolution of InSb Nanoflags Synthesized in Regular Arrays by Chemical Beam Epitaxy. Nanomaterials. 2022; 12(7):1090. https://doi.org/10.3390/nano12071090
Chicago/Turabian StyleVerma, Isha, Valentina Zannier, Vladimir G. Dubrovskii, Fabio Beltram, and Lucia Sorba. 2022. "Understanding the Morphological Evolution of InSb Nanoflags Synthesized in Regular Arrays by Chemical Beam Epitaxy" Nanomaterials 12, no. 7: 1090. https://doi.org/10.3390/nano12071090
APA StyleVerma, I., Zannier, V., Dubrovskii, V. G., Beltram, F., & Sorba, L. (2022). Understanding the Morphological Evolution of InSb Nanoflags Synthesized in Regular Arrays by Chemical Beam Epitaxy. Nanomaterials, 12(7), 1090. https://doi.org/10.3390/nano12071090