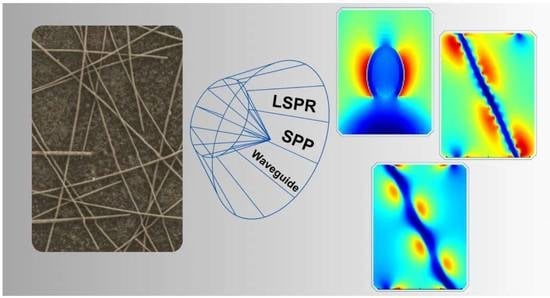
Synergistic Effects of Localized Surface Plasmon Resonance, Surface Plasmon Polariton, and Waveguide Plasmonic Resonance on the Same Material: A Promising Hypothesis to Enhance Organic Solar Cell Efficiency
Abstract
:1. Introduction
1.1. Far-Field Plasmonic Effects: Scattering
1.2. Near-Field Plasmonic Effects
1.2.1. Non-Propagating Modes
1.2.2. Propagating Modes
2. Methods
3. Result and Discussion
3.1. ZAZ Electrode Modeling with One Silver Nanowire
3.2. Modeling a ZAZ Electrode with Multiple Silver Nanowires
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ibrahim Zamkoye, I.; Bouclé, J.; Leclerc, N.; Lucas, B.; Vedraine, S. Silver Nanowire Electrodes Integrated in Organic Solar Cells with Thick Active Layer Based on a Low-Cost Donor Polymer. Solar RRL 2023, 7, 2200756. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative Plasmonic Materials: Beyond Gold and Silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef] [PubMed]
- Boltasseva, A.; Atwater, H.A. Materials Science. Low-Loss Plasmonic Metamaterials. Science 2011, 331, 290–291. [Google Scholar] [CrossRef]
- Wood, R.W. XLII. On a Remarkable Case of Uneven Distribution of Light in a Diffraction Grating Spectrum. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1902, 4, 396–402. [Google Scholar] [CrossRef]
- Rayleigh, L., III. Note on the Remarkable Case of Diffraction Spectra Described by Prof. Wood. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1907, 14, 60–65. [Google Scholar] [CrossRef]
- Otto, A. Excitation of Nonradiative Surface Plasma Waves in Silver by the Method of Frustrated Total Reflection. Z. Für Phys. A Hadron. Nucl. 1968, 216, 398–410. [Google Scholar] [CrossRef]
- Kretschmann, E.; Raether, H. Radiative Decay of Non Radiative Surface Plasmons Excited by Light. Z. Für Naturforschung A 1968, 23, 2135–2136. [Google Scholar] [CrossRef]
- Mayer, A.C.; Scully, S.R.; Hardin, B.E.; Rowell, M.W.; McGehee, M.D. Polymer-Based Solar Cells. Mater. Today 2007, 10, 28–33. [Google Scholar] [CrossRef]
- Falke, S.M.; Rozzi, C.A.; Brida, D.; Maiuri, M.; Amato, M.; Sommer, E.; De Sio, A.; Rubio, A.; Cerullo, G.; Molinari, E.; et al. Coherent Ultrafast Charge Transfer in an Organic Photovoltaic Blend. Science 2014, 344, 1001–1005. [Google Scholar] [CrossRef]
- Vedraine, S.; Torchio, P.; Duché, D.; Flory, F.; Simon, J.-J.; Le Rouzo, J.; Escoubas, L. Intrinsic Absorption of Plasmonic Structures for Organic Solar Cells. Sol. Energy Mater. Sol. Cells 2011, 95, S57–S64. [Google Scholar] [CrossRef]
- N’Konou, K.; Chalh, M.; Monnier, V.; Blanchard, N.P.; Chevolot, Y.; Lucas, B.; Vedraine, S.; Torchio, P. Impact of Ag@SiO2 Core-Shell Nanoparticles on the Photoelectric Current of Plasmonic Inverted Organic Solar Cells. Synth. Met. 2018, 239, 22–28. [Google Scholar] [CrossRef]
- Park, H.I.; Lee, S.; Lee, J.M.; Nam, S.A.; Jeon, T.; Han, S.W.; Kim, S.O. High Performance Organic Photovoltaics with Plasmonic-Coupled Metal Nanoparticle Clusters. ACS Nano 2014, 8, 10305–10312. [Google Scholar] [CrossRef]
- Wang, D.H.; Kim, D.Y.; Choi, K.W.; Seo, J.H.; Im, S.H.; Park, J.H.; Park, O.O.; Heeger, A.J. Enhancement of Donor-Acceptor Polymer Bulk Heterojunction Solar Cell Power Conversion Efficiencies by Addition of Au Nanoparticles. Angew. Chem. Int. Ed. 2011, 50, 5519–5523. [Google Scholar] [CrossRef] [PubMed]
- Chalh, M.; Vedraine, S.; Lucas, B.; Ratier, B. Plasmonic Ag Nanowire Network Embedded in Zinc Oxide Nanoparticles for Inverted Organic Solar Cells Electrode. Sol. Energy Mater. Sol. Cells 2016, 152, 34–41. [Google Scholar] [CrossRef]
- Monestier, F.; Simon, J.-J.; Torchio, P.; Escoubas, L.; Flory, F.; Bailly, S.; de Bettignies, R.; Guillerez, S.; Defranoux, C. Modeling the Short-Circuit Current Density of Polymer Solar Cells Based on P3HT:PCBM Blend. Sol. Energy Mater. Sol. Cells 2007, 91, 405–410. [Google Scholar] [CrossRef]
- Baek, S.-W.; Noh, J.; Lee, C.-H.; Kim, B.; Seo, M.-K.; Lee, J.-Y. Plasmonic Forward Scattering Effect in Organic Solar Cells: A Powerful Optical Engineering Method. Sci. Rep. 2013, 3, 1726. [Google Scholar] [CrossRef]
- Salvador, M.; MacLeod, B.A.; Hess, A.; Kulkarni, A.P.; Munechika, K.; Chen, J.I.L.; Ginger, D.S. Electron Accumulation on Metal Nanoparticles in Plasmon-Enhanced Organic Solar Cells. ACS Nano 2012, 6, 10024–10032. [Google Scholar] [CrossRef] [PubMed]
- Mokkapati, S.; Beck, F.J.; de Waele, R.; Polman, A.; Catchpole, K.R. Resonant Nano-Antennas for Light Trapping in Plasmonic Solar Cells. J. Phys. D Appl. Phys. 2011, 44, 185101. [Google Scholar] [CrossRef]
- Gan, Q.; Bartoli, F.J.; Kafafi, Z.H. Plasmonic-Enhanced Organic Photovoltaics: Breaking the 10% Efficiency Barrier. Adv. Mater. 2013, 25, 2385–2396. [Google Scholar] [CrossRef]
- Masson, J.-F. Portable and Field-Deployed Surface Plasmon Resonance and Plasmonic Sensors. Analyst 2020, 145, 3776–3800. [Google Scholar] [CrossRef]
- Jung, K. Plasmonic Nanocavity Array for Enhanced Upconversion Luminescence. Bull. Korean Chem. Soc. 2019, 40, 91–92. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Xu, W. Surface Plasmon Polaritons: Physics and Applications. J. Phys. D Appl. Phys. 2012, 45, 113001. [Google Scholar] [CrossRef]
- Cohen, M.; Shavit, R.; Zalevsky, Z. Observing Optical Plasmons on a Single Nanometer Scale. Sci. Rep. 2014, 4, 4096. [Google Scholar] [CrossRef]
- Sharma, B.; Frontiera, R.R.; Henry, A.-I.; Ringe, E.; Van Duyne, R.P. SERS: Materials, Applications, and the Future. Mater. Today 2012, 15, 16–25. [Google Scholar] [CrossRef]
- Lim, E.L.; Yap, C.C.; Teridi, M.A.M.; Teh, C.H.; Jumali, M.H.H. A Review of Recent Plasmonic Nanoparticles Incorporated P3HT: PCBM Organic Thin Film Solar Cells. Org. Electron. 2016, 36, 12–28. [Google Scholar] [CrossRef]
- Jang, Y.H.; Jang, Y.J.; Kim, S.; Quan, L.N.; Chung, K.; Kim, D.H. Plasmonic Solar Cells: From Rational Design to Mechanism Overview. Chem. Rev. 2016, 116, 14982–15034. [Google Scholar] [CrossRef]
- Morfa, A.J.; Rowlen, K.L.; Reilly, T.H.; Romero, M.J.; van de Lagemaat, J. Plasmon-Enhanced Solar Energy Conversion in Organic Bulk Heterojunction Photovoltaics. Appl. Phys. Lett. 2008, 92, 013504. [Google Scholar] [CrossRef]
- Moreau, A.; Ciracì, C.; Mock, J.J.; Hill, R.T.; Wang, Q.; Wiley, B.J.; Chilkoti, A.; Smith, D.R. Controlled-Reflectance Surfaces with Film-Coupled Colloidal Nanoantennas. Nature 2012, 492, 86–89. [Google Scholar] [CrossRef]
- Kallmann, H.; Pope, M. Photovoltaic Effect in Organic Crystals. J. Chem. Phys. 1959, 30, 585–586. [Google Scholar] [CrossRef]
- Raether, H. Surface Plasmons on Smooth and Rough Surfaces and on Gratings. In Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 1988; Volume 111. [Google Scholar]
- Li, X.H.; Sha, W.E.I.; Choy, W.C.H.; Fung, D.D.S.; Xie, F.X. Efficient Inverted Polymer Solar Cells with Directly Patterned Active Layer and Silver Back Grating. J. Phys. Chem. C 2012, 116, 7200–7206. [Google Scholar] [CrossRef]
- Zhou, L.; Jiang, X.; Li, Y.; Shi, A.; Chen, J.; Ou, Q.; Liu, H.; Tang, J. Light Extraction of Trapped Optical Modes in Polymer Light-Emitting Diodes with Nanoimprinted Double-Pattern Gratings. ACS Appl. Mater. Interfaces 2014, 6, 18139–18146. [Google Scholar] [CrossRef]
- Suárez, I.; Ferrando, A.; Marques-Hueso, J.; Díez, A.; Abargues, R.; Rodríguez-Cantó, P.J.; Martínez-Pastor, J.P. Propagation Length Enhancement of Surface Plasmon Polaritons in Gold Nano-/Micro-Waveguides by the Interference with Photonic Modes in the Surrounding Active Dielectrics. Nanophotonics 2017, 6, 1109–1120. [Google Scholar] [CrossRef]
- Iqbal, T. Propagation Length of Surface Plasmon Polaritons Excited by a 1D Plasmonic Grating. Curr. Appl. Phys. 2015, 15, 1445–1452. [Google Scholar] [CrossRef]
- Ahn, S.; Rourke, D.; Park, W. Plasmonic Nanostructures for Organic Photovoltaic Devices. J. Opt. 2016, 18, 033001. [Google Scholar] [CrossRef]
- Lassiter, J.B.; McGuire, F.; Mock, J.J.; Ciracì, C.; Hill, R.T.; Wiley, B.J.; Chilkoti, A.; Smith, D.R. Plasmonic Waveguide Modes of Film-Coupled Metallic Nanocubes. Nano Lett. 2013, 13, 5866–5872. [Google Scholar] [CrossRef]
- Chou, C.-H.; Chen, F.-C. Plasmonic Nanostructures for Light Trapping in Organic Photovoltaic Devices. Nanoscale 2014, 6, 8444–8458. [Google Scholar] [CrossRef]
- Li, Q.H.; Zhu, D.; Liu, W.; Liu, Y.; Ma, X.C. Optical Properties of Al-Doped ZnO Thin Films by Ellipsometry. Appl. Surf. Sci. 2008, 254, 2922–2926. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3. [Google Scholar]
- Li, J.-F.; Zhang, Y.-J.; Ding, S.-Y.; Panneerselvam, R.; Tian, Z.-Q. Core–Shell Nanoparticle-Enhanced Raman Spectroscopy. Chem. Rev. 2017, 117, 5002–5069. [Google Scholar] [CrossRef]
- Sun, L.; Wang, J.; Zhang, E.; Tian, Q. Study on the Mechanism of Super-Resolution Near-Field Structure High-Density Optical Data Storage. Jpn. J. Appl. Phys. 2003, 42, 5113. [Google Scholar] [CrossRef]
- Zhao, W.; Qian, D.; Zhang, S.; Li, S.; Inganäs, O.; Gao, F.; Hou, J. Fullerene-Free Polymer Solar Cells with over 11% Efficiency and Excellent Thermal Stability. Adv. Mater. 2016, 28, 4734–4739. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim Zamkoye, I.; Lucas, B.; Vedraine, S. Synergistic Effects of Localized Surface Plasmon Resonance, Surface Plasmon Polariton, and Waveguide Plasmonic Resonance on the Same Material: A Promising Hypothesis to Enhance Organic Solar Cell Efficiency. Nanomaterials 2023, 13, 2209. https://doi.org/10.3390/nano13152209
Ibrahim Zamkoye I, Lucas B, Vedraine S. Synergistic Effects of Localized Surface Plasmon Resonance, Surface Plasmon Polariton, and Waveguide Plasmonic Resonance on the Same Material: A Promising Hypothesis to Enhance Organic Solar Cell Efficiency. Nanomaterials. 2023; 13(15):2209. https://doi.org/10.3390/nano13152209
Chicago/Turabian StyleIbrahim Zamkoye, Issoufou, Bruno Lucas, and Sylvain Vedraine. 2023. "Synergistic Effects of Localized Surface Plasmon Resonance, Surface Plasmon Polariton, and Waveguide Plasmonic Resonance on the Same Material: A Promising Hypothesis to Enhance Organic Solar Cell Efficiency" Nanomaterials 13, no. 15: 2209. https://doi.org/10.3390/nano13152209
APA StyleIbrahim Zamkoye, I., Lucas, B., & Vedraine, S. (2023). Synergistic Effects of Localized Surface Plasmon Resonance, Surface Plasmon Polariton, and Waveguide Plasmonic Resonance on the Same Material: A Promising Hypothesis to Enhance Organic Solar Cell Efficiency. Nanomaterials, 13(15), 2209. https://doi.org/10.3390/nano13152209