Fully Atomistic Molecular Dynamics Simulation of a TIPS-Pentacene:Polystyrene Mixed Film Obtained via the Solution Process
Abstract
:1. Introduction
2. Methods
2.1. Atomistic Models
2.2. Calculation for the Pristine TIPS-P Crystal
2.3. Calculation for the Mixed Solution System
3. Results and Discussions
3.1. Pristine TIPS-P Crystal for Validation of the Force Field
3.2. TIPS-P:aPS:Toluene Ternary System
3.2.1. Mean Squared Displacement
3.2.2. Polymer Configuration
3.2.3. Density Profile
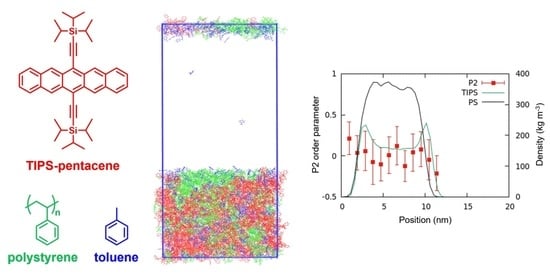
3.2.4. P2 Order Parameter
3.2.5. Surface Profile
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Garnier, F.; Horowitz, G.; Peng, X.; Fichou, D. An All-organic “Soft” Thin Film Transistor with Very High Carrier Mobility. Adv. Mater. 1990, 2, 592–594. [Google Scholar] [CrossRef]
- Liao, C.; Zhang, M.; Yao, M.Y.; Hua, T.; Li, L.; Yan, F. Flexible Organic Electronics in Biology: Materials and Devices. Adv. Mater. 2015, 27, 7493–7527. [Google Scholar] [CrossRef] [PubMed]
- Mano, T.; Nagamine, K.; Ichimura, Y.; Shiwaku, R.; Furusawa, H.; Matsui, H.; Kumaki, D.; Tokito, S. Printed Organic Transistor-Based Enzyme Sensor for Continuous Glucose Monitoring in Wearable Healthcare Applications. ChemElectroChem 2018, 5, 3881–3886. [Google Scholar] [CrossRef]
- Jeong, H.; Baek, S.; Han, S.; Jang, H.; Kim, S.H.; Lee, H.S. Novel Eco-Friendly Starch Paper for Use in Flexible, Transparent, and Disposable Organic Electronics. Adv. Funct. Mater. 2018, 28, 1704433. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Z.; Zhang, T. Flexible Sensing Electronics for Wearable/Attachable Health Monitoring. Small 2017, 13, 1602790. [Google Scholar] [CrossRef]
- Gao, W.; Ota, H.; Kiriya, D.; Takei, K.; Javey, A. Flexible Electronics toward Wearable Sensing. Acc. Chem. Res. 2019, 52, 523–533. [Google Scholar] [CrossRef] [PubMed]
- Rivnay, J.; Owens, R.M.; Malliaras, G.G. The Rise of Organic Bioelectronics. Chem. Mater. 2014, 26, 679–685. [Google Scholar] [CrossRef]
- Xu, L.; Gutbrod, S.R.; Bonifas, A.P.; Su, Y.; Sulkin, M.S.; Lu, N.; Chung, H.J.; Jang, K.I.; Liu, Z.; Ying, M.; et al. 3D Multifunctional Integumentary Membranes for Spatiotemporal Cardiac Measurements and Stimulation across the Entire Epicardium. Nat. Commun. 2014, 5, 3329. [Google Scholar] [CrossRef] [Green Version]
- Isaksson, J.; Kjäll, P.; Nilsson, D.; Robinson, N.; Berggren, M.; Richter-Dahlfors, A. Electronic Control of Ca2+ Signalling in Neuronal Cells Using an Organic Electronic Ion Pump. Nat. Mater. 2007, 6, 673–679. [Google Scholar] [CrossRef]
- Davis, R.L.; Jayaraman, S.; Chaikin, P.M.; Register, R.A. Creating Controlled Thickness Gradients in Polymer Thin Films via Flowcoating. Langmuir 2014, 30, 5637–5644. [Google Scholar] [CrossRef]
- Zou, M.; Ma, Y.; Yuan, X.; Hu, Y.; Liu, J.; Jin, Z. Flexible Devices: From Materials, Architectures to Applications. J. Semicond. 2018, 39, 011010. [Google Scholar] [CrossRef]
- Corzo, D.; Tostado-Blázquez, G.; Baran, D. Flexible Electronics: Status, Challenges and Opportunities. Front. Electron. 2020, 1, 594003. [Google Scholar] [CrossRef]
- Huang, T.-C.; Fukuda, K.; Lo, C.-M.; Yeh, Y.-H.; Sekitani, T.; Someya, T.; Cheng, K.-T. Pseudo-CMOS: A Design Style for Low-Cost and Robust Flexible Electronics. Trans. Electron Devices 2010, 58, 141–150. [Google Scholar] [CrossRef]
- Klauk, H.; Halik, M.; Zschieschang, U.; Schmid, G.; Radlik, W.; Weber, W. High-Mobility Polymer Gate Dielectric Pentacene Thin Film Transistors. J. Appl. Phys. 2002, 92, 5259–5263. [Google Scholar] [CrossRef]
- Sheraw, C.D.; Zhou, L.; Huang, J.R.; Gundlach, D.J.; Jackson, T.N.; Kane, M.G.; Hill, I.G.; Hammond, M.S.; Campi, J.; Greening, B.K.; et al. Organic Thin-Film Transistor-Driven Polymer-Dispersed Liquid Crystal Displays on Flexible Polymeric Substrates. Appl. Phys. Lett. 2002, 80, 1088–1090. [Google Scholar] [CrossRef]
- Sirringhaus, H. Device Physics of Solution-Processed Organic Field-Effect Transistors. Adv. Mater. 2005, 17, 2411–2425. [Google Scholar] [CrossRef]
- Ohe, T.; Kuribayashi, M.; Yasuda, R.; Tsuboi, A.; Nomoto, K.; Satori, K.; Itabashi, M.; Kasahara, J. Solution-Processed Organic Thin-Film Transistors with Vertical Nanophase Separation. Appl. Phys. Lett. 2008, 93, 286. [Google Scholar] [CrossRef]
- Park, S.K.; Jackson, T.N.; Anthony, J.E.; Mourey, D.A. High Mobility Solution Processed 6,13-Bis(Triisopropyl-Silylethynyl) Pentacene Organic Thin Film Transistors. Appl. Phys. Lett. 2007, 91, 6–9. [Google Scholar] [CrossRef]
- Kang, J.; Shin, N.; Do, Y.J.; Prabhu, V.M.; Yoon, D.Y. Structure and Properties of Small Molecule-Polymer Blend Semiconductors for Organic Thin Film Transistors. J. Am. Chem. Soc. 2008, 130, 12273–12275. [Google Scholar] [CrossRef]
- Anthony, J.E. Functionalized Acenes and Heteroacenes for Organic Electronics. Chem. Rev. 2006, 106, 5028–5048. [Google Scholar] [CrossRef]
- Forrest, S.R. Electronic Appliances on Plastic. Nature 2004, 428, 911–918. [Google Scholar] [CrossRef] [PubMed]
- Riera-Galindo, S.; Leonardi, F.; Pfattner, R.; Mas-Torrent, M. Organic Semiconductor/Polymer Blend Films for Organic Field-Effect Transistors. Adv. Mater. Technol. 2019, 4, 1900104. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Local Structure and Dynamics in Solvent-Swollen Polymers. Macromolecules 1996, 29, 4782–4791. [Google Scholar] [CrossRef]
- Steiner, F.; Poelking, C.; Niedzialek, D.; Andrienko, D.; Nelson, J. Influence of Orientation Mismatch on Charge Transport across Grain Boundaries in Tri-Isopropylsilylethynyl (TIPS) Pentacene Thin Films. Phys. Chem. Chem. Phys. 2017, 19, 10854–10862. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Unexpected Diffusion Behavior of Gas Molecules in Crystalline Poly(4-Methyl-1-Pentene). J. Chem. Phys. 1995, 103, 4346–4351. [Google Scholar] [CrossRef]
- Chen, J.; Anthony, J.; Martin, D.C. Thermally Induced Solid-State Phase Transition of Bis(triisopropylsilylethynyl) Pentacene Crystals. J. Phys. Chem. B 2006, 110, 16397–16403. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.; van der Spoel, D.; Lindahl, E.; Hess, B.; the GROMACS Development Team. GROMACS User Manual Version 2016. Available online: https://manual.gromacs.org/documentation/2016/manual-2016.pdf (accessed on 7 January 2023).
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Ke, Q.; Gong, X.; Liao, S.; Duan, C.; Li, L. Effects of thermostats/barostats on physical properties of liquids by molecular dynamics simulations. J. Mol. Liq. 2022, 365, 120116. [Google Scholar] [CrossRef]
- Wong-ekkabut, J.; Karttunen, M. The good, the bad and the user in soft matter simulations. Biochim. Biophys. Acta 2016, 1858, 2529–2538. [Google Scholar] [CrossRef] [PubMed]
- Anthony, J.E.; Brooks, J.S.; Eaton, D.L.; Parkin, S.R. Functionalized Pentacene: Improved Electronic Properties from Control of Solid-State Order. J. Am. Chem. Soc. 2001, 123, 9482–9483. [Google Scholar] [CrossRef] [PubMed]
- Marcon, V.; Fritz, D.; Van Der Vegt, N.F.A. Hierarchical Modelling of Polystyrene Surfaces. Soft Matter 2012, 8, 5585–5594. [Google Scholar] [CrossRef]
- Qian, H.; Sheetz, M.P.; Elson, E.L. Single Particle Tracking. Analysis of Diffusion and Flow in Two-Dimensional Systems. Biophys. J. 1991, 60, 910–921. [Google Scholar] [CrossRef] [Green Version]
- Tarantino, N.; Tinevez, J.Y.; Crowell, E.F.; Boisson, B.; Henriques, R.; Mhlanga, M.; Agou, F.; Israël, A.; Laplantine, E. Tnf and Il-1 Exhibit Distinct Ubiquitin Requirements for Inducing NEMO-IKK Supramolecular Structures. J. Cell Biol. 2014, 204, 231–245. [Google Scholar] [CrossRef]
- Dalmolen, L.G.P.; Picken, S.J.; de Jong, A.F.; de Jeu, W.H. The order parameters <P2> and <P4> in nematic p-alkyl-p′-cyano-biphenyls: Polarized Raman measurements and the influence of molecular association. J. Phys. 1985, 46, 1443–1449. [Google Scholar]
- Kiely, J.D. Quantification of Topographic Structure by Scanning Probe Microscopy. J. Vac. Sci. Technol. B Microelectron. Nanom. Struct. 1997, 15, 1483. [Google Scholar] [CrossRef]
- Bonaccurso, E.; Graf, K. Nanostructuring Effect of Plasma and Solvent Treatment on Polystyrene. Langmuir 2004, 20, 11183–11190. [Google Scholar] [CrossRef] [PubMed]








| w/w% Toluene | # of Toluene | # of TIPS-P | # of aPS Chain | Box [x, y, z] (nm) | Total Time (µs) |
|---|---|---|---|---|---|
| 50 | 2700 | 150 | 150 | 9.5; 19.0; 9.5 | 1 |
| 30 | 1620 | 150 | 150 | 8.7; 8.7; 40.0 | 1 |
| 20 | 1080 | 150 | 150 | 7.8; 7.8; 30.0 | 1 |
| 10 | 540 | 150 | 150 | 7.9; 7.9; 20.0 | 1 |
| 5 | 270 | 150 | 150 | 7.6; 7.6; 20.0 | 1 |
| Toluene Content (w/w%) | Toluene (cm2/s) | TIPS-P (cm2/s) | aPS (cm2/s) | |||
|---|---|---|---|---|---|---|
| 300 K | 333 K | 300 K | 333 K | 300 K | 333 K | |
| 50 | (5.63 ± 0.07) × 10−6 | (1.33 ± 0.01) × 10−5 | (8.0 ± 0.7) × 10−7 | (1.29 ± 0.04) × 10−6 | (5.9 ± 0.2) × 10−7 | (10 ± 1) × 10−7 |
| 20 | (2.5 ± 0.5) × 10−6 | (3 ± 2) × 10−6 | (7.2 ± 0.5) × 10−8 | (2.1 ± 0.4) × 10−7 | (5.1 ± 0.4) × 10−8 | (2.0 ± 0.3) × 10−7 |
| 10 | (1.6 ± 0.1) × 10−6 | (3.4 ± 0.8) × 10−6 | (1.8 ± 0.3) × 10−8 | (7 ± 1) × 10−8 | (1.17 ± 0.08) × 10−8 | (6.8 ± 0.8) × 10−8 |
| 5 | (9 ± 3) × 10−7 | (1.8 ± 0.8) × 10−6 | (4 ± 1) × 10−9 | (1.5 ± 0.4) × 10−8 | (4 ± 1) × 10−9 | (1.2 ± 0.3) × 10−8 |
| Toluene Content (w/w%) | Temperature (K) | (ns) |
|---|---|---|
| 50 | 300 | 0.64 ± 0.03 |
| 50 | 333 | 2.2 ± 0.1 |
| 5 | 300 | 240 ± 20 |
| 5 | 333 | 190 ± 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, T.; De Nicola, A.; Okada, T.; Matsui, H. Fully Atomistic Molecular Dynamics Simulation of a TIPS-Pentacene:Polystyrene Mixed Film Obtained via the Solution Process. Nanomaterials 2023, 13, 312. https://doi.org/10.3390/nano13020312
Suzuki T, De Nicola A, Okada T, Matsui H. Fully Atomistic Molecular Dynamics Simulation of a TIPS-Pentacene:Polystyrene Mixed Film Obtained via the Solution Process. Nanomaterials. 2023; 13(2):312. https://doi.org/10.3390/nano13020312
Chicago/Turabian StyleSuzuki, Tomoka, Antonio De Nicola, Tomoharu Okada, and Hiroyuki Matsui. 2023. "Fully Atomistic Molecular Dynamics Simulation of a TIPS-Pentacene:Polystyrene Mixed Film Obtained via the Solution Process" Nanomaterials 13, no. 2: 312. https://doi.org/10.3390/nano13020312
APA StyleSuzuki, T., De Nicola, A., Okada, T., & Matsui, H. (2023). Fully Atomistic Molecular Dynamics Simulation of a TIPS-Pentacene:Polystyrene Mixed Film Obtained via the Solution Process. Nanomaterials, 13(2), 312. https://doi.org/10.3390/nano13020312