Dimensions of Cellulose Nanocrystals from Cotton and Bacterial Cellulose: Comparison of Microscopy and Scattering Techniques
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of CNC Suspensions
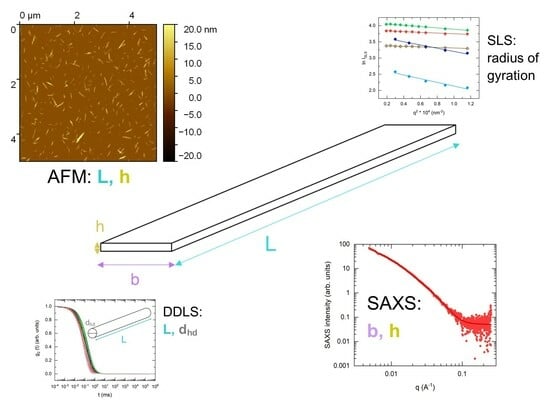
2.3. Experimental Techniques for the Size Characterization of CNC Suspensions
2.4. Data Analysis
- -
- Average length is fixed as obtained from AFM;
- -
- Hydrodynamic cross-section dimension is fixed at either the width or the height as obtained from AFM;
- -
- Length polydispersity σ is fixed at either 0.1, 0.3, 0.5, or 0.8.
3. Results and Discussion
3.1. Atomic Force Microscopy (AFM)
3.2. Small-Angle X-ray Scattering (SAXS)
3.3. Depolarized Dynamic Light Scattering (DDLS)
3.4. Static Light Scattering (SLS)
3.5. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Orts, W.J.; Godbout, L.; Marchessault, R.H.; Revol, J.-F. Enhanced Ordering of Liquid Crystalline Suspensions of Cellulose Microfibrils: A Small Angle Neutron Scattering Study. Macromolecules 1998, 31, 5717–5725. [Google Scholar] [CrossRef]
- Araki, J.; Wada, M.; Kuga, S.; Okano, T. Influence of surface charge on viscosity behavior of cellulose microcrystal suspension. J. Wood Sci. 1999, 45, 258–261. [Google Scholar] [CrossRef]
- Fagbemi, O.D.; Andrew, J.E.; Sithole, B. Beneficiation of wood sawdust into cellulose nanocrystals for application as a bio-binder in the manufacture of particleboard. Biomass Convers. Biorefinery 2021, 13, 11645–11656. [Google Scholar] [CrossRef]
- Kumar, P.; Miller, K.; Kermanshahi-pour, A.; Brar, S.K.; Beims, R.F.; Xu, C.C. Nanocrystalline cellulose derived from spruce wood: Influence of process parameters. Int. J. Biol. Macromol. 2022, 221, 426–434. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Q.; Chang, C.; Zhang, L. Phase transition identification of cellulose nanocrystal suspensions derived from various raw materials. J. App. Polym. Sci. 2017, 135, 45702. [Google Scholar] [CrossRef]
- Mondal, K.; Sakurai, S.; Okahisa, Y.; Goud, V.V.; Katiyar, V. Effect of cellulose nanocrystals derived from Dunaliella tertiolecta marine green algae residue on crystallization behaviour of poly(lactic acid). Carbohydr. Polym. 2021, 261, 117881. [Google Scholar] [CrossRef]
- Sun, B.; Zhang, M.; Hou, Q.; Liu, R.; Wu, T.; Si, C. Further characterization of cellulose nanocrystal (CNC) preparation from sulfuric acid hydrolysis of cotton fibers. Cellulose 2015, 23, 439–450. [Google Scholar] [CrossRef]
- Haouache, S.; Jimenez-Saelices, C.; Cousin, F.; Falourd, X.; Pontoire, B.; Cahier, K.; Jérome, F.; Capron, I. Cellulose nanocrystals from native and mercerized cotton. Cellulose 2022, 29, 1567–1581. [Google Scholar] [CrossRef]
- Miriam de Souza Lima, M.; Borsali, R. Static and Dynamic Light Scattering from Polyelectrolyte Microcrystal Cellulose. Langmuir 2002, 18, 992–996. [Google Scholar] [CrossRef]
- Darpentigny, C.; Molina-Boisseau, S.; Nonglaton, G.; Bras, J.; Jean, B. Ice-templated freeze-dried cryogels from tunicate cellulose nanocrystals with high specific surface area and anisotropic morphological and mechanical properties. Cellulose 2020, 27, 233–247. [Google Scholar] [CrossRef]
- Araki, J.; Kuga, S. Effect of Trace Electrolyte on Liquid Crystal Type of Cellulose Microcrystals. Langmuir 2001, 17, 4493–4496. [Google Scholar] [CrossRef]
- Sommer, A.; Staroszczyk, H. Bacterial cellulose vs. bacterial cellulose nanocrystals as stabilizer agents for O/W pickering emulsions. Food Hydrocoll. 2023, 145, 109080. [Google Scholar] [CrossRef]
- Verma, C.; Chhajed, M.; Gupta, P.; Roy, S.; Maji, P.K. Isolation of cellulose nanocrystals from different waste bio-mass collating their liquid crystal ordering with morphological exploration. Int. J. Biol. Macromol. 2021, 175, 242–253. [Google Scholar] [CrossRef]
- Araki, J.; Wada, M.; Kuga, S.; Okano, T. Flow properties of microcrystalline cellulose suspension prepared by acid treatment of native cellulose. Colloids Surf. A Physicochem. Eng. Asp. 1998, 142, 75–82. [Google Scholar] [CrossRef]
- Vanderfleet, O.M.; Osorio, D.A.; Cranston, E.D. Optimization of cellulose nanocrystal length and surface charge density through phosphoric acid hydrolysis. Phil. Trans. R. Soc. 2017, 376, 20170041. [Google Scholar] [CrossRef]
- Cheng, M.; Qin, Z.; Hu, J.; Liu, Q.; Wei, T.; Li, W.; Ling, Y.; Liu, B. Facile and rapid one–step extraction of carboxylated cellulose nanocrystals by H2SO4/HNO3 mixed acid hydrolysis. Carbohydr. Polym. 2020, 231, 115701. [Google Scholar] [CrossRef]
- Montanari, S.; Roumani, M.; Heux, L.; Vignon, M.R. Topochemistry of Carboxylated Cellulose Nanocrystals Resulting from TEMPO-Mediated Oxidation. Macromolecules 2005, 38, 1665–1671. [Google Scholar] [CrossRef]
- Fan, W.; Li, J.; Wei, L.; Xu, Y. Carboxylated cellulose nanocrystal films with tunable chiroptical properties. Carbohydr. Polym. 2022, 289, 119442. [Google Scholar] [CrossRef]
- Zhong, L.; Fu, S.; Peng, X.; Zhan, H.; Sun, R. Colloidal stability of negatively charged cellulose nanocrystalline in aqueous systems. Carbohydr. Polym. 2012, 90, 644–649. [Google Scholar] [CrossRef]
- da Silva Maradini, G.; Oliveira, M.P.; da Silva Guanaes, G.M.; Passamani, G.Z.; Carreira, L.G.; Boschetti, W.T.; Monteiro, S.N.; Pereira, A.C.; de Oliveira, B.F. Characterization of Polyester Nanocomposites Reinforced with Conifer Fiber Cellulose Nanocrystals. Polymers 2020, 12, 2838. [Google Scholar] [CrossRef]
- Feng, K.; Dong, C.; Gao, Y.; Jin, Z. A Green and Iridescent Composite of Cellulose Nanocrystals with Wide Solvent Resistance and Strong Mechanical Properties. ACS Sustain. Chem. Eng. 2021, 9, 6764–6775. [Google Scholar] [CrossRef]
- Torlopov, M.A.; Vaseneva, I.N.; Mikhaylov, V.I.; Martakov, I.S.; Moskalev, A.A.; Koval, L.A.; Zemskaya, N.V.; Paderin, N.M.; Sitnikov, P.A. Pickering emulsions stabilized by partially acetylated cellulose nanocrystals for oral administration: Oils effect and in vivo toxicity. Cellulose 2021, 28, 2365–2385. [Google Scholar] [CrossRef]
- Sun, Z.; Eyley, S.; Guo, Y.; Salminen, R.; Thielemans, W. Synergistic effects of chloride anions and carboxylated cellulose nanocrystals on the assembly of thick three-dimensional high-performance polypyrrole-based electrodes. J. Energy Chem. 2022, 70, 492–501. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Tian, B.; Xiao, H.; Chen, W.; Wu, H.; Jia, J. Immobilization of bismuth oxychloride on cellulose nanocrystal for photocatalytic sulfonylation of arylacetylenic acids with sodium arylsulfinates under visible light. Arab. J. Chem. 2022, 15, 103708. [Google Scholar] [CrossRef]
- Blockx, J.; Verfaillie, A.; Deschaume, O.; Bartic, C.; Muylaert, K.; Thielemans, W. Glycine betaine grafted nanocellulose as an effective and bio-based cationic nanocellulose flocculant for wastewater treatment and microalgal harvesting. Nanoscale Adv. 2021, 3, 4133–4144. [Google Scholar] [CrossRef]
- Revol, J.-F.; Bradford, H.; Giasson, J.; Marchessault, R.H.; Gray, D.G. Helicoidal self-ordering of cellulose microfibrils in aqueous suspension. Int. J. Biol. Macromol. 1992, 14, 170–172. [Google Scholar] [CrossRef]
- Hirai, A.; Inui, O.; Horii, F.; Tsuji, M. Phase Separation Behavior in Aqueous Suspensions of Bacterial Cellulose Nanocrystals Prepared by Sulfuric Acid Treatment. Langmuir 2009, 25, 497–502. [Google Scholar] [CrossRef]
- Esmaeili, M.; George, K.; Rezvan, G.; Taheri-Qazvini, N.; Zhang, R.; Sadati, M. Capillary Flow Characterizations of Chiral Nematic Cellulose Nanocrystal Suspensions. Langmuir 2022, 38, 2192–2204. [Google Scholar] [CrossRef]
- Browne, C.; Raghuwanshi, V.S.; Garnier, G.; Batchelor, W. Modulating the chiral nematic structure of cellulose nanocrystal suspensions with electrolytes. J. Colloid Interface Sci. 2023, 650, 1064–1072. [Google Scholar] [CrossRef]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Stroobants, A.; Lekkerkerker, H.N.W.; Odijk, T. Effect of Electrostatic Interaction on the Liquid Crystal Phase Transition in Solutions of Rodlike Polyelectrolytes. Macromolecules 1986, 19, 2232–2238. [Google Scholar] [CrossRef]
- Marchessault, R.H.; Morehead, F.F.; Koch, M.J. Some hydrodynamic properties of neutral suspensions of cellulose crystallites as related to size and shape. J. Colloid Sci. 1961, 16, 327–344. [Google Scholar] [CrossRef]
- Terech, P.; Chazeau, L.; Cavaillé, J.Y. A Small-Angle Scattering Study of Cellulose Whiskers in Aqueous Suspensions. Macromolecules 1999, 32, 1872–1875. [Google Scholar] [CrossRef]
- Ureña-Benavides, E.E.; Kitchens, C.L. Static light scattering of triaxial nanoparticle suspensions in the RayleighGans-Debye regime: Application to cellulose nanocrystals. RSC Adv. 2012, 2, 1096–1105. [Google Scholar] [CrossRef]
- Mao, Y.; Liu, K.; Zhan, C.; Geng, L.; Chu, B.; Hsiao, B.S. Characterization of Nanocellulose Using Small-Angle Neutron, X-ray, and Dynamic Light Scattering Techniques. J. Phys. Chem. B 2017, 121, 1340–1351. [Google Scholar] [CrossRef]
- Lahiji, R.R.; Xu, X.; Reifenberger, R.; Raman, A.; Rudie, A.; Moon, R.J. Atomic Force Microscopy Characterization of Cellulose Nanocrystals. Langmuir 2010, 26, 4480–4488. [Google Scholar] [CrossRef]
- Bushell, M.; Meija, J.; Chen, M.; Batchelor, W.; Browne, C.; Cho, J.-Y.; Clifford, C.A.; Al-Rekabi, Z.; Vanderfleet, O.M.; Cranston, E.D.; et al. Particle size distributions for cellulose nanocrystals measured by atomic force microscopy: An interlaboratory comparison. Cellulose 2021, 28, 1387–1403. [Google Scholar] [CrossRef]
- Johns, M.A.; Lam, C.; Zakani, B.; Melo, L.; Grant, E.R.; Cranston, E.D. Comparison of cellulose nanocrystal dispersion in aqueous suspension via new and established analytical techniques. Cellulose 2023, 30, 8259–8274. [Google Scholar] [CrossRef]
- Elazzouzi-Hafraoui, S.; Nishiyama, Y.; Putaux, J.-L.; Heux, L.; Dubreuil, F.; Rochas, C. The Shape and Size Distribution of Crystalline Nanoparticles Prepared by Acid Hydrolysis of Native Cellulose. Biomacromolecules 2008, 9, 57–65. [Google Scholar] [CrossRef]
- Meija, J.; Bushell, M.; Couillard, M.; Beck, S.; Bonevich, J.; Cui, K.; Foster, J.; Will, J.; Fox, D.; Cho, W.; et al. Particle Size Distributions for Cellulose Nanocrystals Measured by Transmission Electron Microscopy: An Interlaboratory Comparison. Anal. Chem. 2020, 92, 13434–13442. [Google Scholar] [CrossRef]
- Campano, C.; Lopez-Exposito, P.; Gonzalez-Aguilera, L.; Blanco, Á.; Negro, C. In-depth characterization of the aggregation state of cellulose nanocrystals through analysis of transmission electron microscopy images. Carbohydr. Polym. 2021, 254, 117271. [Google Scholar] [CrossRef]
- Qian, H. Major Factors Influencing the Size Distribution Analysis of Cellulose Nanocrystals Imaged in Transmission Electron Microscopy. Polymers 2021, 13, 3318. [Google Scholar] [CrossRef]
- Magazzù, A.; Marcuello, C. Investigation of Soft Matter Nanomechanics by Atomic Force Microscopy and Optical Tweezers: A Comprehensive Review. Nanomaterials 2023, 13, 963. [Google Scholar] [CrossRef]
- Meinander, K.; Jensen, T.N.; Simonsen, S.B.; Helveg, S.; Lauritsen, J.V. Quantification of tip-broadening in non-contact atomic force microscopy with carbon nanotube tips. Nanotechnology 2012, 23, 405705. [Google Scholar] [CrossRef]
- Bercea, M.; Navard, P. Shear Dynamics of Aqueous Suspensions of Cellulose Whiskers. Macromolecules 2000, 33, 6011–6016. [Google Scholar] [CrossRef]
- Kaushik, M.; Basu, K.; Benoit, C.; Cirtiu, C.M.; Vali, H.; Moores, A. Cellulose Nanocrystals as Chiral Inducers: Enantioselective Catalysis and Transmission Electron Microscopy 3D Characterization. J. Am. Chem. Soc. 2015, 137, 6124–6127. [Google Scholar] [CrossRef]
- Buesch, C.; Smith, S.W.; Eschbach, P.; Conley, J.F., Jr.; Simonsen, J. The Microstructure of Cellulose Nanocrystal Aerogels as Revealed by Transmission Electron Microscope Tomography. Biomacromolecules 2016, 17, 2956–2962. [Google Scholar] [CrossRef]
- Majoinen, J.; Haataja, J.S.; Appelhans, D.; Lederer, A.; Olszewska, A.; Seitsonen, J.; Aseyev, V.; Kontturi, E.; Rosilo, H.; Österberg, M.; et al. Supracolloidal Multivalent Interactions and Wrapping of Dendronized Glycopolymers on Native Cellulose Nanocrystals. J. Am. Chem. Soc. 2014, 136, 866–869. [Google Scholar] [CrossRef]
- Majoinen, J.; Hassinen, J.; Haataja, J.S.; Rekola, H.T.; Kontturi, E.; Kostiainen, M.A.; Ras, R.H.A.; Törmä, P.; Ikkala, O. Chiral Plasmonics Using Twisting along Cellulose Nanocrystals as a Template for Gold Nanoparticles. Adv. Mater. 2016, 28, 5262–5267. [Google Scholar] [CrossRef]
- Bai, L.; Kämäräinen, T.; Ziang, W.; Majoinen, J.; Seitsonen, J.; Grande, R.; Huan, S.; Liu, L.; Fan, Y.; Rojas, O.J. Chirality from Cryo-Electron Tomograms of Nanocrystals Obtained by Lateral Disassembly and Surface Etching of Never-Dried Chitin. ACS Nano 2020, 14, 6921–6930. [Google Scholar] [CrossRef]
- Zhang, F.; Ilavsky, J. Ultra-Small-Angle X-ray Scattering of Polymers. Polym. Rev. 2010, 50, 59–90. [Google Scholar] [CrossRef]
- Schütz, C.; Agthe, M.; Fall, A.B.; Gordeyeva, K.; Guccini, V.; Salajková, M.; Plivelic, T.S.; Lagerwall, J.P.F.; Salazar-Alvarez, G.; Bergström, L. Rod Packing in Chiral Nematic Cellulose Nanocrystal Dispersions Studied by Small-Angle X-ray Scattering and Laser Diffraction. Langmuir 2015, 31, 6507–6513. [Google Scholar] [CrossRef]
- Rosén, T.; Wang, R.; Zhan, C.; He, H.; Chodankar, S.; Hsiao, B.S. Cellulose nanofibrils and nanocrystals in confined flow: Single-particle dynamics to collective alignment revealed through scanning small-angle X-ray scattering and numerical simulations. Phys. Rev. E 2020, 101, 032610. [Google Scholar] [CrossRef]
- Cherhal, F.; Cousin, F.; Capron, I. Influence of Charge Density and Ionic Strength on the Aggregation Process of Cellulose Nanocrystals in Aqueous Suspension, as Revealed by Small-Angle Neutron Scattering. Langmuir 2015, 31, 5596–5602. [Google Scholar] [CrossRef]
- Cherhal, F.; Cousin, F.; Capron, I. Structural Description of the Interface of Pickering Emulsions Stabilized by Cellulose Nanocrystals. Biomacromolecules 2016, 17, 496–502. [Google Scholar] [CrossRef]
- Uhlig, M.; Fall, A.; Weller, S.; Lehmann, M.; Prévost, S.; Wågberg, L.; von Klitzing, R.; Nyström, G. Two-Dimensional Aggregation and Semidilute Ordering in Cellulose Nanocrystals. Langmuir 2016, 32, 442–450. [Google Scholar] [CrossRef]
- Azzam, F.; Frka-Petesic, B.; Semeraro, E.F.; Cousin, F.; Jean, B. Small-Angle Neutron Scattering Reveals the Structural Details of Thermosensitive Polymer-Grafted Cellulose Nanocrystal Suspensions. Langmuir 2020, 36, 8511–8519. [Google Scholar] [CrossRef]
- Delepierre, G.; Eyley, S.; Thielemans, W.; Weder, C.; Cranston, E.D.; Zoppe, J.O. Patience is a Virtue: Self-Assembly and Physico-Chemical Properties of Cellulose Nanocrystal Allomorphs. Nanoscale 2020, 12, 17480–17493. [Google Scholar] [CrossRef]
- Jakubek, Z.J.; Chen, M.; Couillard, M.; Leng, T.; Liu, L.; Zou, S.; Baxa, U.; Clogston, J.D.; Hamad, W.Y.; Johnston, L.J. Characterization challenges for a cellulose nanocrystal reference material: Dispersion and particle size distributions. J. Nanopart. Res. 2018, 20, 98. [Google Scholar] [CrossRef]
- Miriam de Souza Lima, M.; Wong, J.T.; Paillet, M.; Borsali, R.; Pecora, R. Translational and Rotational Dynamics of Rodlike Cellulose Whiskers. Langmuir 2003, 19, 24–29. [Google Scholar] [CrossRef]
- Khouri, S.; Shams, M.; Tam, K.C. Determination and prediction of physical properties of cellulose nanocrystals from dynamic light scattering measurements. J. Nanopart. Res. 2014, 16, 2499. [Google Scholar] [CrossRef]
- Van Rie, J.; Schütz, C.; Gençer, A.; Lombardo, S.; Gasser, U.; Kumar, S.; Salazar-Alvarez, G.; Kang, K.; Thielemans, W. Anisotropic Diffusion and Phase Behavior of Cellulose Nanocrystal Suspensions. Langmuir 2019, 35, 2289–2302. [Google Scholar] [CrossRef]
- Mazloumi, M.; Johnston, L.J.; Jakubek, Z.J. Dispersion, stability and size measurements for cellulose nanocrystals by static multiple light scattering. Cellulose 2018, 25, 5751–5768. [Google Scholar] [CrossRef]
- Nagalakshmaiah, M.; Pignon, F.; El Kissi, N.; Dufresne, A. Surface adsorption of triblock copolymer (PEO–PPO–PEO) on cellulose nanocrystals and their melt extrusion with polyethylene. RSC Adv. 2016, 6, 66224–66232. [Google Scholar] [CrossRef]
- Gicquel, E.; Bras, J.; Rey, C.; Putaux, J.-L.; Pignon, F.; Jean, B.; Martin, C. Impact of sonication on the rheological and colloidal properties of highly concentrated cellulose nanocrystal suspensions. Cellulose 2019, 26, 7619–7634. [Google Scholar] [CrossRef]
- Vasconcelos, N.F.; Andrade Feitosa, J.P.; Portela da Gama, F.M.; Saraiva Morais, J.P.; Andrade, F.K.; Moreira de Souza Filho, M.S.; de Freitas Rosa, M. Bacterial cellulose nanocrystals produced under different hydrolysis conditions: Properties and morphological features. Carbohydr. Polym. 2017, 155, 425–431. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Cent. Eur. J. Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Nayuk, R.; Huber, K. Formfactors of Hollow and Massive Rectangular Parallelepipeds at Variable Degree of Anisometry. Z. Phys. Chem. 2012, 226, 837–854. [Google Scholar] [CrossRef]
- Boluk, Y.; Danumah, C. Analysis of cellulose nanocrystal rod lengths by dynamic light scattering and electron microscopy. J. Nanopart. Res. 2014, 16, 2174. [Google Scholar] [CrossRef]
- Tirado, M.M.; García de la Torre, J. Rotational dynamics of rigid, symmetric top macromolecules. Application to circular cylinders. J. Chem. Phys. 1980, 73, 1986–1993. [Google Scholar] [CrossRef]
- Bhattacharjee, S. DLS and zeta potential—What they are and what they are not? J. Control. Release 2016, 235, 337–351. [Google Scholar] [CrossRef]










| Sample | c*, vol% | cSAXS, vol% | cDDLS, vol% |
|---|---|---|---|
| sulfated cotton CNCs | 0.25 | 0.10 | 0.05 |
| sulfated-carboxylated cotton CNCs | 0.28 | 0.10 | 0.05 |
| carboxylated cotton CNCs | 0.16 | 0.05 | 0.05 |
| sulfated bacterial CNCs, 1st batch | 0.06 | 0.02 | 0.01 |
| sulfated bacterial CNCs, 2nd batch | 0.09 | 0.02 | 0.01 |
| Parameter | Sulfated Cotton CNCs | Sulfated-Carboxylated Cotton CNCs | Carboxylated Cotton CNCs | Sulfated Bacterial CNCs, 1st Batch | Sulfated Bacterial CNCs, 2nd Batch |
|---|---|---|---|---|---|
| , nm | 189 | 203 | 277 | 382 | 370 |
| σL | 0.31 ± 0.02 | 0.27 ± 0.02 | 0.27 ± 0.01 | 0.36 ± 0.03 | 0.41 ± 0.03 |
| , nm | 42 | 38 | 40 | 40 | 39 |
| σb | 0.27 ± 0.05 | 0.28 ± 0.02 | 0.28 ± 0.02 | 0.29 ± 0.02 | 0.25 ± 0.01 |
| , nm | 6.8 | 7.8 | 8.0 | 6.9 | 7.8 |
| σh | 0.18 ± 0.01 | 0.38 ± 0.05 | 0.34 ± 0.05 | 0.27 ± 0.03 | 0.38 ± 0.05 |
| : ratio | 4.5 | 5.3 | 6.9 | 9.6 | 9.5 |
| : ratio | 6.2 | 4.9 | 5.0 | 5.8 | 5.0 |
| Parameter | Sulfated Cotton CNCs | Sulfated-Carboxylated Cotton CNCs | Carboxylated Cotton CNCs | Sulfated Bacterial CNCs, 1st Batch | Sulfated Bacterial CNCs, 2nd Batch |
|---|---|---|---|---|---|
| , nm | 28 | 20 | 31 | 26 | 29 |
| σb | 0.28 ± 0.02 | 0.34 ± 0.03 | 0.29 ± 0.03 | 0.29 ± 0.05 | 0.35 ± 0.06 |
| , nm | 4.5 | 5.0 | 5.1 | 5.0 | 3.9 |
| σh | 0.42 ± 0.02 | 0.29 ± 0.01 | 0.42 ± 0.01 | 0.29 ± 0.08 | 0.44 ± 0.02 |
| : ratio | 6.2 | 4.0 | 6.1 | 5.2 | 7.4 |
| Parameter | Sulfated Cotton CNCs | Sulfated-Carboxylated Cotton CNCs | Carboxylated Cotton CNCs | Sulfated Bacterial CNCs, 1st Batch | Sulfated Bacterial CNCs, 2nd Batch |
|---|---|---|---|---|---|
| , nm | 28.4 | 9.6 | 25.0 | 5.7 | 10.0 |
| (AFM), nm | 42 | 38 | 40 | 40 | 39 |
| (AFM), nm | 6.8 | 7.8 | 8.0 | 6.9 | 7.8 |
| σL (DDLS) | 0.50 | 0.45 | 0.53 | 0.81 | 0.78 |
| σL (AFM) | 0.31 | 0.27 | 0.27 | 0.36 | 0.41 |
| Method | Sulfated Cotton CNCs | Sulfated-Carboxylated Cotton CNCs | Carboxylated Cotton CNCs | Sulfated Bacterial CNCs, 1st Batch | Sulfated Bacterial CNCs, 2nd Batch |
|---|---|---|---|---|---|
| AFM | 56 ± 18 | 60 ± 17 | 81 ± 23 | 111 ± 41 | 107 ± 46 |
| SLS | 57 ± 2 | 51 ± 2 | 78 ± 1 | 122 ± 6 | 131 ± 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grachev, V.; Deschaume, O.; Lang, P.R.; Lettinga, M.P.; Bartic, C.; Thielemans, W. Dimensions of Cellulose Nanocrystals from Cotton and Bacterial Cellulose: Comparison of Microscopy and Scattering Techniques. Nanomaterials 2024, 14, 455. https://doi.org/10.3390/nano14050455
Grachev V, Deschaume O, Lang PR, Lettinga MP, Bartic C, Thielemans W. Dimensions of Cellulose Nanocrystals from Cotton and Bacterial Cellulose: Comparison of Microscopy and Scattering Techniques. Nanomaterials. 2024; 14(5):455. https://doi.org/10.3390/nano14050455
Chicago/Turabian StyleGrachev, Vladimir, Olivier Deschaume, Peter R. Lang, Minne Paul Lettinga, Carmen Bartic, and Wim Thielemans. 2024. "Dimensions of Cellulose Nanocrystals from Cotton and Bacterial Cellulose: Comparison of Microscopy and Scattering Techniques" Nanomaterials 14, no. 5: 455. https://doi.org/10.3390/nano14050455
APA StyleGrachev, V., Deschaume, O., Lang, P. R., Lettinga, M. P., Bartic, C., & Thielemans, W. (2024). Dimensions of Cellulose Nanocrystals from Cotton and Bacterial Cellulose: Comparison of Microscopy and Scattering Techniques. Nanomaterials, 14(5), 455. https://doi.org/10.3390/nano14050455