Dependence of the Structural and Magnetic Properties on the Growth Sequence in Heterostructures Designed by YbFeO3 and BaFe12O19
Abstract
:1. Introduction
2. Experimental Section
2.1. PLD Growth of Multiferroic Heterostructure Systems
2.2. High-Resolution and X-ray Diffraction Reciprocal Space Mapping
2.3. X-ray Reflectivity and Profile Density
2.4. Transmission Electron Microscopy
2.5. Vibrating Sample Magnetometry
3. Results
3.1. Characterization of the Heterostructures M1 and M2
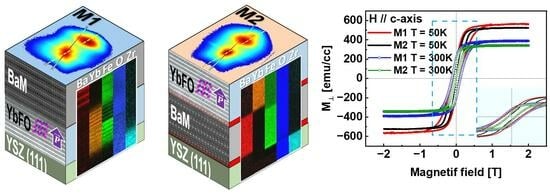
3.2. Effect of Growth Sequence on the Magnetic Properties
4. Conclusions and Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, D.; Harward, I.; Linderman, K.; Economou, E.; Nie, Y.; Celinski, Z. Properties of ferroelectric/ferromagnetic thin film heterostructures. J. Appl. Phys. 2014, 115, 17D713. [Google Scholar] [CrossRef]
- Dun, Y.; Chen, J.; An, D.; Chen, D.; Chen, Y.; Li, Y. Voltage control of millimeter-wave ferromagnetic resonance in multiferroic heterostructures thin films. Phys. Lett. A 2020, 384, 126639. [Google Scholar] [CrossRef]
- Bodeux, R.; Michau, D.; Maglione, M.; Josse, M. Thin films sputtered from Ba2NdFeNb4O15 multiferroic targets on BaFe12O19 coated substrates. Mater. Res. Bull. 2016, 81, 49–54. [Google Scholar] [CrossRef]
- Hajlaoui, T.; Harnagea, C.; Pignolet, A. Magnetoelectric coupling in room temperature multiferroic Ba2EuFeNb4O15/BaFe12O19 epitaxial heterostructures grown by laser ablation. Nanomaterials 2023, 13, 761. [Google Scholar] [CrossRef]
- Srinivasan, G.; Zavislyak, I.V.; Tatarenko, A.S. Millimeter-wave magnetoelectric effects in bilayers of barium hexaferrite and lead zirconate titanate. Appl. Phys. Lett. 2006, 89, 152508. [Google Scholar] [CrossRef]
- Srinath, S.; Frey, N.A.; Heindl, R.; Srikanth, H.; Coffey, K.R.; Dudney, N.J. Growth and characterization of sputtered BSTO/BaM multilayers. J. Appl. Phys. 2005, 97, 10J115. [Google Scholar] [CrossRef]
- Das, J.; Kalinikos, B.A.; Barman, A.R.; Patton, C.E. Multifunctional dual-tunable low loss ferrite-ferroelctric heterostructures for microwave devices. Appl. Phys. Lett. 2007, 91, 172516. [Google Scholar] [CrossRef]
- Das, J.; Song, Y.Y.; Wu, M. Electric-field control of ferromagnetic resonance in monolithic BaFe12O19–Ba0.5Sr0.5TiO3BaFe12O19–Ba0.5Sr0.5TiO3 heterostructures. J. Appl. Phys. 2010, 108, 043911. [Google Scholar] [CrossRef]
- Zandalazini, C.I.; Oliva, M.I.; Ferrero, J.C. Structural and magnetic characterization of BaTiO3–BaFe12O19 bilayer thin films: Interface effects on the magnetic properties of barium hexaferrite layer. Ceram. Int. 2021, 47, 19384–19393. [Google Scholar] [CrossRef]
- Portugal, R.J.; Peko, J.-C.M.; Hernandes, A.C.; Guaran, C.A.; Guerr, J.D.S. Synthesis and electrical properties of PZT/BaFe12O19 multiferroic ceramics. Key Eng. Mater. 2012, 512, 1291–1295. [Google Scholar] [CrossRef]
- Guerra, J.D.S.; Pal, M.; Portugal, R.J.; Cótica, L.F.; Santos, I.A.; Guo, R.; Bhalla, A.S. Multiferroism and magnetoelectric coupling in (PbZr0.65Ti0.35O3)0.97–(BaFe12O19)0.03 ceramic composites. J. Appl. Phys. 2013, 114, 224113. [Google Scholar] [CrossRef]
- Guerra, J.D.S.; McIntosh, R.; M’Peko, J.-C.; Hernandes, A.C.; Guo, R.; Bhalla, A.S. Frequency dielectric response of ferroelectric–magnetic ceramic composites like PbZr0.65Ti0.35O3–BaFe12O19. Ceram. Int. 2015, 41, 7091–7096. [Google Scholar] [CrossRef]
- Nergis, B.; Bauer, S.; Jin, X.; Seemann, K.; Horak, L.; Schneider, R.; Holy, V.; Ulrich, S.; Baumbach, T. Effect of the laser fluence on the microstructure and the relating magnetic properties of BaFe12O19 films grown on YSZ(111) by PLD for optimized perpendicular recording. J. Mater. Sci. 2023, 58, 718–739. [Google Scholar] [CrossRef]
- Bauer, S.; Nergis, B.; Jin, X.; Schneider, R.; Wang, D.; Kübel, C.; Holy, V.; Horak, L.; Seemann, K.; Ulrich, S.; et al. Effect of underlayer quality on microstructure, stoichiometry, and magnetic properties of hexaferrite BaFe12O19 grown on YSZ(111) by PLD. Langmuir 2023, 39, 14308–14327. [Google Scholar] [CrossRef]
- Xu, X.; Wang, W. Multiferroic hexagonal ferrites (h-RFeO3, R = Y, Dy-Lu): A brief experimental review. Mod. Phys. Lett. B 2014, 28, 1430008. [Google Scholar] [CrossRef]
- Jeong, Y.K.; Lee, J.H.; Ahn, S.J.; Song, S.W.; Jang, H.M.; Choi, H.; Scott, J.F. Structurally tailored hexagonal ferroelectricity and multiferroism in epitaxial YbFeO3 thin-film heterostructures. J. Am. Chem. Soc. 2012, 134, 1450–1453. [Google Scholar] [CrossRef]
- Iida, H.; Koizumi, T.; Uesu, Y.; Kohn, K.; Ikeda, N.; Mori, S.; Haumont, R.; Janolin, P.E.; Kiat, J.M.; Fukunaga, M.; et al. Ferroelectricity and ferrimagnetism of hexagonal YbFeO3 thin films. J. Phys. Soc. Jpn. 2012, 81, 024719. [Google Scholar] [CrossRef]
- Cao, S.; Sinha, K.; Zhang, X.; Wang, X.; Yin, Y.; N’Diaye, A.T.; Wang, J.; Keavney, D.J.; Paudel, T.R.; Liu, Y.; et al. Electronic structure and direct observation of ferrimagnetism in multiferroic hexagonal YbFeO3. Phys. Rev. B 2017, 95, 224428. [Google Scholar] [CrossRef]
- Rai, R.C.; Horvatits, C.; Mckenna, D.; Du Hart, J. Structural studies and physical properties of hexagonal-YbFeO3 thin films. AIP Adv. 2019, 9, 015019. [Google Scholar] [CrossRef]
- Xu, X.X.; Yun, Y.; Buragohain, P.; Thind, A.; Yin, Y.; Li, X.; Jiang, X.; Mishra, R.; Gruverman, A. Absence of critical thickness in improper ferroelectric hexagonal-YbFeO3 thin films. Res. Sq. 2020. [Google Scholar] [CrossRef]
- Yun, Y.; Buragohain, P.; Thind, A.S.; Yin, Y.; Li, X.; Jiang, X.; Mishra, R.; Gruverman, A.; Xu, X. Spontaneous polarization in an ultrathin improper-ferroelectric/dielectric bilayer in a capacitor structure at cryogenic temperatures. Phys. Rev. Appl. 2022, 18, 034071. [Google Scholar] [CrossRef]
- Li, X.; Yun, Y.; Thind, A.S.; Yin, Y.; Li, Q.; Wang, W.; N’Diaye, A.T.; Mellinger, C.; Jiang, X.; Mishra, R.; et al. Domain-wall magnetoelectric coupling in multiferroic hexagonal YbFeO3 films. Sci. Rep. 2023, 13, 1775. [Google Scholar] [CrossRef] [PubMed]
- Tikhanova, S.; Seroglazova, A.; Chebanenko, M.; Nevedomskiy, V.; Popkov, V. Effect of TiO2 additives on the stabilization of h-YbFeO3 and promotion of photo-fenton activity of o-YbFeO3/h-YbFeO3/r-TiO2 nanocomposites. Materials 2022, 15, 8273. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Hua, Z.; Geng, C.; Ma, N. Facile synthesis of novel YbFeO3–BiFeO3 composite for highly sensitive ppb-level acetone sensing at low temperature. J. Mater. Sci. Mater. Electron. 2023, 34, 1588. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, Y.; Yang, S.; Yang, Z.; Xu, X. Effect of interface on epitaxy and magnetism in h-RFeO3/Fe3O4/Al2O3 films (R = Lu, Yb). J. Phys. Condens. Matter 2017, 29, 164001. [Google Scholar] [CrossRef] [PubMed]
- Fu, Q.; Zhuang, N.; Hu, X.; Chen, J. Substrate influence on the structure and properties of YbFeO3 film. Mater. Res. Express 2019, 6, 126120. [Google Scholar] [CrossRef]
- Bibes, M.; Balcells, L.; Valencia, S.; Fontcuberta, J.; Wojcik, M.; Jedryka, E.; Nadolski, S. Nanoscale multiphase separation at La2/3Ca1/3MnO3/SrTiO3 interfaces. Phys. Rev. Lett. 2001, 87, 067210. [Google Scholar] [CrossRef] [PubMed]
- Gan, Q.; Rao, R.A.; Eom, C.B.; Garrett, J.L.; Lee, M. Direct measurement of strain effects on magnetic and electrical properties of epitaxial SrRuO3 thin film. Appl. Phys. Lett. 1998, 72, 978. [Google Scholar] [CrossRef]
- Vrejoiu, I.; Ziese, M.; Setzer, A.; Esquinazi, P.D.; Birajdar, B.I.; Lotnyk, A.; Alexe, M.; Hesse, D. Interfacial strain effects in epitaxial multiferroic heterostructures of PbZrxTi1−xO3/La0.7Sr0.3MnO3PbZr grown by pulsed-laser deposition. Appl. Phys. Lett. 2008, 92, 152506. [Google Scholar] [CrossRef]
- Choi, E.-M.; Sim, K.I.; Burch, K.S.; Lee, Y.H. Emergent multifunctional magnetic proximity in van der Waals layered heterostructures. Adv. Sci. 2022, 9, 2200186. [Google Scholar] [CrossRef]
- Huang, H.; Zhai, X.; Wang, J.; Meng, D.; Yun, Y.; Ma, C.; Zheng, X.; Wu, L.; Pan, H.; Fu, Z.; et al. Effect of interface defects on the magnetoresistance in Bi4Ti3O12/(La, Sr)Mn1−xO3 heterostructures. J. Mater. Sci. 2018, 53, 9627–9634. [Google Scholar] [CrossRef]
- Vafaee, M.; Finizio, S.; Deniz, H.; Hesse, D.; Zabel, H.; Jakob, G.; Kläui, M. The effect of interface roughness on exchange bias in La0.7Sr0.3MnO3–BiFeO3 heterostructures. Appl. Phys. Lett. 2016, 108, 072401. [Google Scholar] [CrossRef]
- Chen, B.; Gauquelin, N.; Green, R.J.; Verbeeck, J.; Rijnders, G.; Koster, G. Asymmetric cation intermixing, magnetic coupling in LaMnO3/LaFeO3 heterostructures. Front. Phys. 2021, 9, 698154. [Google Scholar] [CrossRef]
- Neumann, R.F.; Bahiana, M.; Binggeli, N. Magnetic properties of La0.67Sr0.33MnO3/BiFeO3(001) heterojunctions: Chemically abrupt vs. atomic intermixed interface. Europhys. Lett. 2012, 100, 67002. [Google Scholar] [CrossRef]
- Huang, Z.; Ariando; Wang, X.R.; Rusydi, A.; Chen, J.; Yang, H.; Venkatesan, T. Interface engineering and emergent phenomena in oxide heterostructures. Adv. Mater. 2018, 30, 1802439. [Google Scholar] [CrossRef] [PubMed]
- Malozemoff, A.P. Random-field model of exchange anisotropy at rough ferromagnetic-antiferromagnetic interfaces. Phys. Rev. B 1987, 35, 3679–3682. [Google Scholar] [CrossRef] [PubMed]
- Jensen, P.J.; Dreyssé, H.; Kiwi, M. Magnetic reordering in the vicinity of a ferromagnetic/antiferromagnetic interface. Eur. Phys. J. B 2005, 46, 541–551. [Google Scholar] [CrossRef]
- Husain, S.; Harris, I.; Gao, G.; Li, X.; Meisenheimer, P.; Shi, C.; Kavle, P.; Choi, C.H.; Kim, T.Y.; Kang, D.; et al. Low-temperature grapho-epitaxial La-substituted BiFeO3 on metallic perovskite. Nat. Commun. 2024, 15, 479. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, K.; Hou, Y. Magnetic Heterostructures: Interface Control to Optimize Magnetic Property and Multifunctionality. ACS Appl. Mater. Interfaces 2020, 12, 36811–36822. [Google Scholar] [CrossRef]
- Liu, K.; Zhang, R.; Li, J.; Zhang, S. Atomic-Scale Structural Properties in NiCo2O4/CuFe2O4 Bilayer Heterostructures on (001)-MgAl2O4 Substrate Regulated by Film Thickness. Materials 2024, 17, 871. [Google Scholar] [CrossRef]
- Koon, N.C. Calculations of exchange bias in thin films with ferromagnetic/antiferromagnetic interfaces. Phys. Rev. Lett. 1997, 78, 4865–4868. [Google Scholar] [CrossRef]
- Folven, E.; Scholl, A.; Young, A.; Retterer, S.T.; Boschker, J.E.; Tybell, T.; Takamura, Y.; Grepstad, J.K. Crossover from spin-flop coupling to collinear spin alignment in antiferromagnetic/ferromagnetic nanostructures. Nano Lett. 2012, 12, 2386–2390. [Google Scholar] [CrossRef] [PubMed]
- Schulthess, T.C.; Butler, W.H. Consequences of spin-flop coupling in exchange biased films. Phys. Rev. Lett. 1998, 81, 4516–4519. [Google Scholar] [CrossRef]
- Berkowitz, A.E.; Takano, K. Exchange anisotropy—A review. J. Magn. Magn. Mater. 1999, 200, 552–570. [Google Scholar] [CrossRef]
- Dong, S.; Yamauchi, K.; Yunoki, S.; Yu, R.; Liang, S.; Moreo, A.; Liu, J.-M.; Picozzi, S.; Dagotto, E. Exchange bias driven by the Dzyaloshinskii-Moriya interaction and ferroelectric polarization at G-type antiferromagnetic perovskite interfaces. Phys. Rev. Lett. 2009, 103, 127201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Krishnan, K.M. Epitaxial exchange-bias systems: From fundamentals to future spin-orbitronics. Mater. Sci. Eng. R 2016, 105, 1–20. [Google Scholar] [CrossRef]
- Olsen, F.K.; Hallsteinsen, I.; Arenholz, E.; Tybell, T.; Folven, E. Coexisting spin-flop coupling and exchange bias in LaFeO3/La0.7Sr0.3MnO3 heterostructures. Phys. Rev. B 2019, 99, 134411. [Google Scholar] [CrossRef]
- Gibert, M.; Viret, M.; Torres-Pardo, A.; Piamonteze, C.; Zubko, P.; Jaouen, N.; Tonnerre, J.-M.; Mougin, A.; Fowlie, J.; Catalano, S.; et al. Interfacial control of magnetic properties at LaMnO3/LaNiO3 interfaces. Nano Lett. 2015, 15, 7355–7361. [Google Scholar] [CrossRef] [PubMed]
- Paratt, L.G. Surface studies of solids by total reflection of X-rays. Phys. Rev. 1954, 95, 359–369. [Google Scholar] [CrossRef]
- Cliff, W.; Lorimer, G.W. The quantitative analysis of thin specimens. J. Microsc. 1975, 103, 203. [Google Scholar] [CrossRef]
- Zehner, J.; Soldatov, I.; Schneider, S.; Heller, R.; Khojasteh, N.B.; Schiemenz, S.; Fähler, S.; Nielsch, K.; Schäfer, R.; Leistner, K. Voltage-controlled deblocking of magnetization reversal in thin films by tunable domain wall interactions and pinning sites. Adv. Electron. Mater. 2020, 6, 2000406. [Google Scholar] [CrossRef]
- Williamson, G.K.; Hall, W.H. X-ray line broadening from filed aluminum and wolfram. Acta Metall. 1953, 1, 22. [Google Scholar] [CrossRef]
- Ji, T.Z.; Sun, L.; Miao, B.F.; Millev, Y.T.; Ding, H.F. General nature of the step-induced frustration at ferromagnetic/antiferromagnetic interfaces: Topological origin and quantitative understanding. New J. Phys. 2019, 21, 123045. [Google Scholar]
- Shirk, B.T.; Buessem, W.R. Temperature dependence of Ms and K1 of BaFe12O19 and SrFe12O19 single crystals. J. Appl. Phys. 1969, 40, 1294–1296. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, B.; Zhang, W.; Zhou, S.; Schmidt, H. Ultra large coercivity in barium ferrite thin films prepared by magnetron sputtering. J. Magn. Magn. Mater. 2010, 322, 1859–1862. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, F.; Wu, W.; Zhao, G.M. Unusual temperature dependence of the magnetic anisotropy constant in barium ferrite BaFe12O19. J. Appl. Phys. 2011, 110, 096107. [Google Scholar] [CrossRef]
- Singh, H.K.; Mohapatra, P.P.; Sahu, S.; Dobbidi, P. Dielectric and temperature dependent magnetic studies of Al3+ substituted Ba0.4La0.1Sr0.5AlxFe12-xO19 hexaferrite for microwave application. Mater. Sci. Eng. B 2022, 284, 115876. [Google Scholar] [CrossRef]
- Kronmüller, H.; Durst, K.D.; Sagawa, M. Analysis of the magnetic hardening mechanism in RE-FeB permanent magnets. J. Magn. Magn. Mater. 1988, 74, 291. [Google Scholar] [CrossRef]
- Peña-Garcia, R.; Guerra, Y.; de Souza, F.R.; Gonçalves, L.A.P.; Padrón-Hernández, E. The extended Bloch’s law in yttrium iron garnet doped with Zn, Ni and Co. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 103, 354–360. [Google Scholar] [CrossRef]
- Liu, B.-H.; Ding, J.; Dong, Z.-L.; Boothroyd, C.-B.; Yin, J.-H.; Yi, J.-B. Microstructural evolution and its influence on the magnetic properties of CoFe2O4 powders during mechanical milling. Phys. Rev. B 2006, 74, 184427. [Google Scholar] [CrossRef]
- Bance, S.; Seebacher, B.; Schrefl, T.; Exl, L.; Winklhofer, M.; Hrkac, G.; Zimanyi, G.; Shoji, T.; Yano, M.; Sakuma, N.; et al. Grain-size dependent demagnetizing factors in permanent magnets. J. Appl. Phys. 2014, 116, 233903. [Google Scholar] [CrossRef]
- Kou, X.-C.; Kronmüller, H.; Givord, D.; Rossignol, M.F. Coercivity mechanism of sintered Pr17Fe75B8 and Pr17Fe53B30 permanent magnets. Phys. Rev. B 1994, 50, 3849. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Zhao, X.; Liu, W.; Li, Y.; Liu, L.; Song, Y.; Xie, Y.; Zhao, X.; Zhang, Z. Coercivity mechanism and magnetization reversal in anisotropic Ce-(Y)-Pr-Fe-B films. Materials 2021, 14, 4680. [Google Scholar] [CrossRef] [PubMed]
- Qiu, L.; Zhao, L.; Weng, X.; Shen, L.; Zhao, G.; Wang, F.; Xie, L. A hybrid coercivity mechanism for exchange-coupled nanocomposite permanent magnets. J. Rare Earths 2019, 37, 1030–1033. [Google Scholar] [CrossRef]
- Kumar, P.S.A.; Joy, P.A.; Date, S.K. Comparison of the irreversible thermomagnetic behaviour of some ferro- and ferrimagnetic systems. Bull. Mater. Sci. 2000, 23, 97–101. [Google Scholar] [CrossRef]








| (a) | ||||||||||
| d(11-2)YSZ [Å] | d(111)YSZ [Å] | aM1YbFO [Å] | aM2YbFO [Å] | cM1YbFO [Å] | cM2YbFO [Å] | aM1BaM [Å] | aM2BaM [Å] | cM1BaM [Å] | cM2BaM [Å] | |
| M1 | 2.100 ± 0.001 | 2.969 ± 0.001 | 6.0221 ± 0.001 | 11.693 ± 0.001 | 5.8151 ± 0.001 | 23.25 ± 0.001 | ||||
| M2 | 2.100 ± 0.001 | 2.969 ± 0.001 | 5.9881 ± 0.001 | 11.7149 ± 0.001 | 5.967 ± 0.001 | 23.2942 ± 0.001 | ||||
| (b) | ||||||||||
| fM1YbFO/YSZ [%] | fM1BaM/YbFO [%] | fM2BaM/YSZ [%] | fM2YbFO/BaM [%] | |||||||
| M1 | −4.42 compressive | −3.56 compressive | ||||||||
| M2 | −5.30 compressive | 0.35 tensile | ||||||||
| (c) | ||||||||||
| εM1YbFO// [%] | εM1YbFO⊥ [%] | εM1BaM// [%] | εM1BaM⊥ [%] | εM2BaM// [%] | εM2BaM⊥ [%] | εM2YbFO// [%] | εM2YbFO⊥ [%] | |||
| M1 | 0.96 Tensile | −0.08 Compressive | −1.3 Compressive | 0.29 Tensile | ||||||
| M2 | 1.3 Tensile | 0.48 Tensile | 0.39 Tensile | 0.11 Tensile | ||||||
| (a) | ||||||||
| BaM thickness ThBaM [nm] XRR | YbFO thickness ThYbFO [nm] XRR | Mass density ρBaM [g/cm3] XRR | Mass density ρYbFO [g/cm3] XRR | Transition region YbFO/YSZ RM1Tr1 [nm] XRR | Transition region BaM/YbFO RM1Tr2 [nm] XRR | Transition region BaM/YSZ RM2Tr1 [nm] XRR | Transition region YbFO/BaM RM2Tr2 [nm] XRR | |
| M1 | 61.0 ± 0.2 | 58.8 ± 0.2 | 5.24 ± 0.05 ≅ ρBaFe12O19 = 5.296 g/cm3 | 8.38 ± 0.05 > ρ YbFeO3 = 6.8 g/cm3 | 2.81 ± 0.1 | 8.2 ± 0.1 | ||
| M2 | 70.0 ± 0.2 | 65.0 ± 0.2 | 3.86 ± 0.05 < ρBaFe12O19 = 5.296 g/cm3 | 7.14 ± 0.07 slightly > ρ YbFeO3 = 6.8 g/cm3 | 3.95 ± 0.1 | 10.3 ± 0.1 | ||
| (b) | ||||||||
| BaM thickness ThBaM [nm] TEM | YbFO thickness ThYbFO [nm] TEM | YbFO/YSZ RM1int1 [nm] EDX profiles | YbFO/YSZ RM1int2 [nm] EDX profiles | BaM/YbFO RM1int3 [nm] EDX profiles | BaM/YSZ RM2int1 [nm] EDX profiles | BaM/YSZ RM2int2 [nm] EDX profiles | BaM/YbFO RM2int3 [nm] EDX profiles | |
| M1 | 63 ± 0.2 | 53 ± 0.2 | 2.75 < Th < 4.6 1.85 ± 0.05 nm Interdiffusion of Zr atoms | 4.6 < Th < 6.5 1.9 ± 0.05 nm Residual Zr atoms | 4.5 < Th < 7 2.5 ± 0.05 nm Sharp interface without intermixing | |||
| M2 | 67 ± 0.2 | 74 ± 0.2 | 1.25< Th < 2.9 1.65 ± 0.05 nm Interdiffusion of Zr atoms | 2.9 < Th < 4.8 1.9 ± 0.05 nm Fe rich phase | 4.2 < Th < 12.93 8.7 ± 0.05 nm Chemical intermixing | |||
| (c) | ||||||||
| BaM thickness ThBaM [nm] TEM | YbFO thickness ThYbFO [nm] TEM | RM1YbFO. χ [at %] | RM1BaM χ [at %] | RM2YbFO. χ [at %] | RM2BaM χ [at %] | |||
| M1 | 63 ± 0.2 | 53 ± 0.2 | χYb (Max)= 30 ± 1 <χYb> = 23.57 <χFe> = 27.12 (see Figure 5i) | χBaM (Max) = 7 ± 0.5 <χBa> = 3.7 <χFe> = 54.03 (see Figure 6n) | ||||
| M2 | 67 ± 0.2 | 74 ± 0.2 | χYb (max) = 18 ± 0.5 Large scan <χYb > = 19.85, <χFe> = 17.97 Atomic resolution <χYb > = 13.89, <χFe > = 18.53 | χBaM (Max) = 6 ± 0.5 Large scan <χBa > = 3.18, <χFe> = 36.77 Atomic resolution <χBaM> = 3.39, <χFe> = 27.1 | ||||
| Moment at Saturation T = 0 K Ms⊥(0) [emu/cc] | Exponent P | Curie Temperature Tc [K] | Anisotropy Constant K1, T = 0 K1(0) [N/m2] | Exponent P | Microstructural Parameter α | Demagnetization Factor Neff | |
|---|---|---|---|---|---|---|---|
| M1 | MsM1⊥(0) = 573.43 ± 5.97 | PM1Ms⊥ = 1.277 ± 0.040 | TM1c = 723.5 ± 5 | KM11(0) = 3.5E+6 ± 4.4E+3 | PM1K1 = 1.432 ± 0.060 | αM1 = 0.116 | NM1eff = 0.072 |
| M2 | MsM2⊥(0) = 513.77 ± 5.68 | PM2Ms⊥ = 1.253 ± 0.037 | TM2c = 730.6 ± 5 | KM21(0) = 2.1E+6 ± 2.6E+3 | PM2K1 = 1.861 ± 0.093 | αM2 = 0.041 | NM2eff = −0.0026 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bauer, S.; Nergis, B.; Jin, X.; Schneider, R.; Wang, D.; Kübel, C.; Machovec, P.; Horak, L.; Holy, V.; Seemann, K.; et al. Dependence of the Structural and Magnetic Properties on the Growth Sequence in Heterostructures Designed by YbFeO3 and BaFe12O19. Nanomaterials 2024, 14, 711. https://doi.org/10.3390/nano14080711
Bauer S, Nergis B, Jin X, Schneider R, Wang D, Kübel C, Machovec P, Horak L, Holy V, Seemann K, et al. Dependence of the Structural and Magnetic Properties on the Growth Sequence in Heterostructures Designed by YbFeO3 and BaFe12O19. Nanomaterials. 2024; 14(8):711. https://doi.org/10.3390/nano14080711
Chicago/Turabian StyleBauer, Sondes, Berkin Nergis, Xiaowei Jin, Reinhard Schneider, Di Wang, Christian Kübel, Petr Machovec, Lukas Horak, Vaclav Holy, Klaus Seemann, and et al. 2024. "Dependence of the Structural and Magnetic Properties on the Growth Sequence in Heterostructures Designed by YbFeO3 and BaFe12O19" Nanomaterials 14, no. 8: 711. https://doi.org/10.3390/nano14080711
APA StyleBauer, S., Nergis, B., Jin, X., Schneider, R., Wang, D., Kübel, C., Machovec, P., Horak, L., Holy, V., Seemann, K., Baumbach, T., & Ulrich, S. (2024). Dependence of the Structural and Magnetic Properties on the Growth Sequence in Heterostructures Designed by YbFeO3 and BaFe12O19. Nanomaterials, 14(8), 711. https://doi.org/10.3390/nano14080711