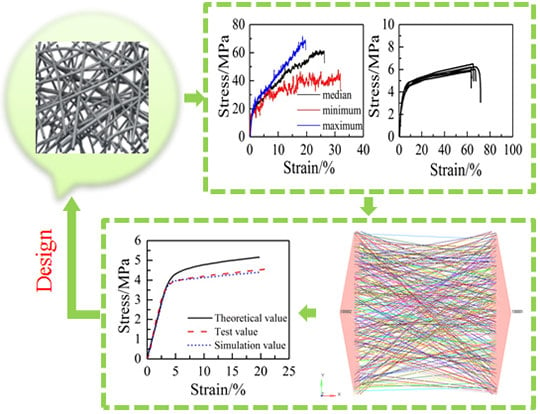
A Tensile Constitutive Relationship and a Finite Element Model of Electrospun Nanofibrous Mats
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Morphological Characterization
2.3. Mechanical Characterization
2.4. Tensile Analysis of Single Fibers
3. Experimental Results
3.1. Single Fibers
3.2. Mats Characterization
4. Tensile Constitutive Relationship
4.1. Straight Fibers
4.2. Curved Fibers
4.3. Elastic-Plastic Constitutive Model of Fibrous Mats
5. Results and Discussion
5.1. Finite Element Modeling
5.2. Parameter Analysis
5.2.1. Length-Width Ratio Parameter
5.2.2. Porosity
5.2.3. Fiber Curvature
5.3. Model Validation
6. Conclusions
- a greater length-width ratio and porosity of specimen results in a lower elasticity modulus of nanofibrous mats; a greater number of bending fibers in nanofibrous mats is related to a smaller radius of curvature and a lower elasticity modulus of nanofibrous mats;
- elastic-plastic axial stress-strain behavior, including elasticity modulus and yield modulus;
- a re-orientation of nanofibers toward the loading direction, which is anisotropic behavior;
- a smaller included angle between the single nanofiber and tensile loading direction, which occurs before the fiber entered the plastic deformation zone.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| yield stress of single fiber (MPa) | equivalent cross-sectional area of single fiber (μm2) | ||
| break stress of single fiber (MPa) | equivalent stress of single fiber (MPa) | ||
| break strain of single fiber (%) | equivalent strain of single fiber | ||
| initial elastic modulus of mats (MPa) | equivalent elastic modulus of single fiber (MPa) | ||
| yield stress of mats (MPa) | P | porosity of mats (%) | |
| yield strain of mats (%) | 1 − P | volume fraction of fibers (%) | |
| strengthening modulus of mats (MPa) | SR | stiffness ratio | |
| break stress of mats (MPa) | modulus of single fiber (MPa) | ||
| break strain of mats (%) | stress of single fiber (MPa) | ||
| tensile force (μN) | modulus of mats (MPa) | ||
| tensile force on single fiber (μN) | strain of mats (%) | ||
| angle between the fiber and the stretching direction (°) | N | number of units | |
| displacement in the direction of the fiber (μm) | D | fiber diameter (μm) | |
| length of single fiber (μm) | T | thickness of mats (μm) | |
| A | single fiber cross-sectional area (μm2) | R | curvature radius (μm) |
| elastic modulus of single fiber (MPa) | k | aspect ratio of mats | |
| displacement in the stretch direction (μm) | υ | Poisson’s ratio | |
| L | length (μm) | p | Ratio coefficient |
References
- Leung, V.; Ko, F. Biomedical applications of nanofibers. Polym. Adv. Technol. 2011, 22, 350–365. [Google Scholar] [CrossRef]
- Gnavi, S.; Fornasari, B.E.; Tonda-Turo, C.; Laurano, R.; Zanetti, M.; Ciardelli, G.; Geuna, S. The Effect of Electrospun Gelatin Fibers Alignment on Schwann Cell and Axon Behavior and Organization in the Perspective of Artificial Nerve Design. Int. J. Mol. Sci. 2015, 16, 12925–12942. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Lv, Y. Application of Collagen Scaffold in Tissue Engineering: Recent Advances and New Perspectives. Polymers 2016, 8, 42. [Google Scholar] [CrossRef]
- Gentile, P.; Ferreira, A.M.; Callaghan, J.T.; Miller, C.A.; Atkinson, J.; Freeman, C.; Hatton, P.V. Multilayer Nanoscale Encapsulation of Biofunctional Peptides to Enhance Bone Tissue Regeneration In Vivo. Adv. Healthc. Mater. 2017, 6, 1601182. [Google Scholar] [CrossRef] [PubMed]
- Nakielski, P.; Kowalczyk, T.; Zembrzycki, K.; Kowalewski, T.A. Experimental and numerical evaluation of drug release from nanofiber mats to brain tissue. J. Biomed. Mater. Res. B 2014, 103, 282–291. [Google Scholar] [CrossRef] [PubMed]
- Weng, L.; Xie, J. Smart Electrospun Nanofibers for Controlled Drug Release: Recent Advances and New Perspectives. Curr. Pharm. Des. 2015, 21, 1944–1959. [Google Scholar] [CrossRef] [PubMed]
- Giannitelli, S.M.; Accoto, D.; Trombetta, M.; Rainer, A. Current trends in the design of scaffolds for computer-aided tissue engineering. Acta Biomater. 2014, 10, 580–594. [Google Scholar] [CrossRef] [PubMed]
- Haque, M.A.; Saif, M.T.A. A review of MEMS-based microscale and nanoscale tensile and bending testing. Exp. Mech. 2003, 43, 248–255. [Google Scholar] [CrossRef]
- Yu, M.F.; Dyer, M.J.; Skidmore, G.D.; Rohrs, H.W.; Lu, X.K.; Ausman, K.D.; Von Ehr, J.R.; Ruoff, R.S. Three-dimensional manipulation of carbon nanotubes under a scanning electron microscope. Nanotechnology 1999, 10, 244–252. [Google Scholar] [CrossRef]
- Yu, M.F.; Lourie, O.; Dyer, M.J.; Moloni, K.; Kelly, T.F.; Ruoff, R.S. Strength and Breaking Mechanism of Multiwalled Carbon Nanotubes Under Tensile Load. Science 2000, 287, 637–640. [Google Scholar] [CrossRef] [PubMed]
- Hwang, K.Y.; Kim, S.D.; Kim, Y.W.; Yu, W.R. Mechanical characterization of nanofibers using a nanomanipulator and atomic force microscope cantilever in a scanning electron microscope. Polym. Test. 2010, 29, 375–380. [Google Scholar] [CrossRef]
- Lin, Y.; Clark, D.M.; Yu, X.; Zhong, Z.; Liu, K.; Reneker, D.H. Mechanical properties of polymer nanofibers revealed by interaction with streams of air. Polymer 2012, 53, 782–790. [Google Scholar] [CrossRef]
- Kolluru, P.V.; Chasiotis, I. Interplay of molecular and specimen length scales in the large deformation mechanical behavior of polystyrene nanofibers. Polymer 2015, 56, 507–515. [Google Scholar] [CrossRef]
- Tan, E.P.S.; Ng, S.Y.; Lim, C.T. Tensile testing of a single ultrafine polymeric fiber. Biomaterials 2005, 26, 1453–1456. [Google Scholar] [CrossRef] [PubMed]
- Ridruejo, A.; González, C.; Llorca, J. A constitutive model for the in-plane mechanical behavior of nonwoven fabrics. Int. J. Solids Struct. 2012, 49, 2215–2229. [Google Scholar] [CrossRef]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Kallmes, O.; Corte, H. The structure of paper I. The statistical geometry of an ideal two dimensional fiber network. Tappi J. 1960, 43, 737–752. [Google Scholar]
- Carlsson, L.A.; Lindstrom, T. A shear-lag approach to the tensile strength of paper. Compos. Sci. Technol. 2005, 65, 183–189. [Google Scholar] [CrossRef]
- Räisänen, V.I.; Alava, M.J.; Nieminen, R.M. Failure of planar fiber networks. J. Appl. Phys. 1997, 82, 3747–3753. [Google Scholar] [CrossRef]
- Backer, S.; Petterson, D.R. Some Principles of Nonwoven Fabrics. Text. Res. J. 1960, 30, 704–711. [Google Scholar] [CrossRef]
- Bais-Singh, S.; Goswami, B.C. Theoretical Determination of the Mechanical Response of Spun-bonded Nonwovens. J. Text. Inst. 1995, 86, 271–288. [Google Scholar] [CrossRef]
- Liao, T.; Adanur, S.; Drean, J.Y. Predicting the Mechanical Properties of Nonwoven Geotextiles with the Finite Element Method. Text. Res. J. 1997, 67, 753–760. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Kouznetsova, V.; Brekelmans, W.A.M.; Baaijens, F.P.T. An approach to micro-macro modeling of heterogeneous materials. Comput. Mech. 2001, 27, 37–48. [Google Scholar] [CrossRef]
- Stylianopoulos, T.; Barocas, V.H. Volume-averaging theory for the study of the mechanics of collagen networks. Comput. Methods Appl. Mech. Eng. 2007, 196, 2981–2990. [Google Scholar] [CrossRef]
- Petterson, D.R. On the Mechanics of Non-Woven Fabrics. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1958. [Google Scholar]
- Silberstein, M.N.; Pai, C.L.; Rutledge, G.C.; Boyce, M.C. Elastic–plastic behavior of non-woven fibrous mats. J. Mech. Phys. Solids 2012, 60, 295–318. [Google Scholar] [CrossRef]
- Hou, X.; Acar, M.; Silberschmidt, V.V. 2D finite element analysis of thermally bonded nonwoven materials: Continuous and discontinuous models. Comput. Mater. Sci. 2009, 46, 700–707. [Google Scholar] [CrossRef]
- Hou, X.; Acar, M.; Silberschmidt, V.V. Finite element simulation of low-density thermally bonded nonwoven materials: Effect of orientation distribution function and arrangement of bond points. Comput. Mater. Sci. 2011, 50, 1292–1298. [Google Scholar] [CrossRef] [Green Version]
- Hou, X.; Acar, M.; Silberschmidt, V.V. Non-uniformity of deformation in low-density thermally bonded nonwoven material: Effect of microstructure. J. Mater. Sci. 2011, 46, 307–315. [Google Scholar] [CrossRef] [Green Version]
- Sabuncuoglu, B.; Acar, M.; Silberschmidt, V.V. A parametric finite element analysis method for low-density thermally bonded nonwovens. Comput. Mater. Sci. 2012, 52, 164–170. [Google Scholar] [CrossRef] [Green Version]
- Farukh, F.; Demirci, E.; Sabuncuoglu, B.; Acar, M.; Pourdeyhimi, B.; Silberschmidt, V.V. Numerical modelling of damage initiation in low-density thermally bonded nonwovens. Comput. Mater. Sci. 2012, 64, 112–115. [Google Scholar] [CrossRef] [Green Version]
- Farukh, F.; Demirci, E.; Sabuncuoglu, B.; Acar, M.; Pourdeyhimi, B.; Silberschmidt, V.V. Numerical analysis of progressive damage in nonwoven fibrous networks under tension. Int. J. Solids Struct. 2014, 51, 1670–1685. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Jang, C.H.; Kim, G.H. A polycaprolactone/silk-fibroin nanofibrous composite combined with human umbilical cord serum for subacute tympanic membrane perforation; an in vitro and in vivo study. J. Mater. Chem. B 2014, 2, 2703–2713. [Google Scholar] [CrossRef]
- Kharaziha, M.; Fathi, M.H.; Edris, H. Development of novel aligned nanofibrous composite membranes for guided bone regeneration. J. Mech. Behav. Biomed. 2013, 24, 9–20. [Google Scholar] [CrossRef] [PubMed]
- D’Amore, A.; Stella, J.A.; Wagner, W.R.; Sacks, M.S. Characterization of the complete fiber network topology of planar fibrous tissues and scaffolds. Biomaterials 2010, 31, 5345–5354. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yu, W. Orientation image analysis of electrospun submicro-fibers based on Hough transform and Regionprops function. Text. Res. J. 2016, 87. [Google Scholar] [CrossRef]
- Kumar, V.; Rawal, A. Elastic moduli of electrospun mats: Importance of fiber curvature and specimen dimensions. J. Mech. Behav. Biomed. 2017, 72, 6–13. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Xiong, J. Effect of the Distribution of Fiber Orientation on the Mechanical Properties of Silk Fibroin/Polycaprolactone Nanofiber Mats. J. Eng. Fibers Fabr. 2017, 12, 17–28. [Google Scholar]
- Wang, R.; Xu, B.; Li, C. Accurate fiber orientation measurements in nonwovens using a multi-focus image fusion technique. Text. Res. J. 2013, 84, 115–124. [Google Scholar] [CrossRef]
- Wang, R.W.; Wu, X.Y.; Wang, S.Y.; Xu, B. Automatic identification of ramie and cotton fibers using characteristics in longitudinal view, part 1: Locating capture of fiber images. Text. Res. J. 2009, 79, 1251–1261. [Google Scholar] [CrossRef]
- Rutledge, G.C.; Lowery, J.L.; Pai, C.L. Characterization by Mercury Porosimetry of Nonwoven Fiber Media with Deformation. J. Eng. Fibers Fabr. 2009, 4, 1–13. [Google Scholar]
- Kwon, I.K.; Kidoaki, S.; Matsuda, T. Electrospun nano to microfiber fabrics made of biodegradable copolyesters: Structural characteristics, mechanical properties and cell adhesion potential. Biomaterials 2005, 26, 3929–3939. [Google Scholar] [CrossRef] [PubMed]
- Plastics-Determination of Tensile Properties—Part 1: General Principles. Available online: https://www.iso.org/standard/56045.html (accessed on 4 January 2018).
- Plastics-Determination of Tensile Properties—Part 3: Test Conditions for Films and Sheets. Available online: https://www.iso.org/standard/4594.html (accessed on 4 January 2018).
- Yi, P.; Peng, L.; Liu, N.; Lai, X.; Ni, J. A micromechanics elastic–plastic constitutive model for sintered stainless steel fiber felt. Mater. Des. 2013, 51, 876–885. [Google Scholar] [CrossRef]
- Engelmayr, G.C.; Sacks, M.S. A structural model for the flexural mechanics of nonwoven tissue engineering scaffolds. J. Biomech. Eng. 2006, 128, 610–622. [Google Scholar] [CrossRef] [PubMed]
- Pai, C.L. Morphology and Mechanical Properties of Electrospun Polymeric Fibers and Their Nonwoven Fabrics. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2011; pp. 101–103. [Google Scholar]
- Pai, C.; Boyce, M.C.; Rutledge, G.C. On the importance of fiber curvature to the elastic moduli of electrospun nonwoven fiber meshes. Polymer 2011, 52, 6126–6133. [Google Scholar] [CrossRef]
















| Property | Average | Minimum | Maximum | CV |
|---|---|---|---|---|
| (MPa) | 1717 | 1550 | 1900 | 0.09 |
| (MPa) | 18 | 15 | 23 | 0.10 |
| (MPa) | 60 | 43 | 68 | 0.17 |
| 0.26 | 0.20 | 0.32 | 0.17 |
| Property | Average | Minimum | Maximum | CV |
|---|---|---|---|---|
| (MPa) | 98 | 75 | 120 | 0.16 |
| (MPa) | 3.9 | 3.2 | 4.4 | 0.12 |
| 0.049 | 0.044 | 0.052 | 0.06 | |
| (MPa) | 2.6 | 2.3 | 3.0 | 0.11 |
| (MPa) | 6.14 | 5.83 | 6.49 | 0.04 |
| 0.665 | 0.635 | 0.715 | 0.06 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Pan, Z.; Xiong, J. A Tensile Constitutive Relationship and a Finite Element Model of Electrospun Nanofibrous Mats. Nanomaterials 2018, 8, 29. https://doi.org/10.3390/nano8010029
Yin Y, Pan Z, Xiong J. A Tensile Constitutive Relationship and a Finite Element Model of Electrospun Nanofibrous Mats. Nanomaterials. 2018; 8(1):29. https://doi.org/10.3390/nano8010029
Chicago/Turabian StyleYin, Yunlei, Zhongxiang Pan, and Jie Xiong. 2018. "A Tensile Constitutive Relationship and a Finite Element Model of Electrospun Nanofibrous Mats" Nanomaterials 8, no. 1: 29. https://doi.org/10.3390/nano8010029
APA StyleYin, Y., Pan, Z., & Xiong, J. (2018). A Tensile Constitutive Relationship and a Finite Element Model of Electrospun Nanofibrous Mats. Nanomaterials, 8(1), 29. https://doi.org/10.3390/nano8010029