The Band-Gap Modulation of Graphyne Nanoribbons by Edge Quantum Entrapment
Abstract
:1. Introduction
2. Principles
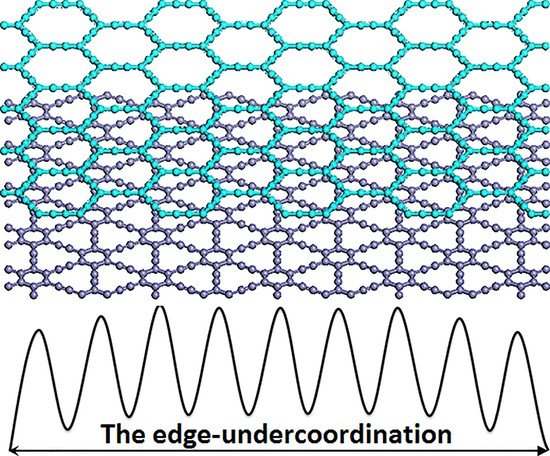
2.1. Size Effect and BOLS Approximation
2.2. Calculations and Experimental Details
3. Results and Discussion
3.1. Optimized Structures of (α, β)-GYNRs
3.2. Band Structures of (α, β)-Graphyne
3.3. Band Structures of (α, β)-GYNRs
3.4. Edge-Atomic-Charge Entrapment
3.5. Size Dependence of the Band-Gap
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hirsch, A. The Era of Carbon Allotropes. Nat. Mater. 2010, 9, 868–871. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Xie, L.; Lee, K.K.; Hu, Z.; Tan, S.; Chen, W.; Sow, C.H.; Chen, K.; Liu, Y.; Wee, A.T.S. Controllable Unzipping for Intramolecular Junctions of Graphene Nanoribbons and Single-Walled Carbon Nanotubes. Nat. Commun. 2013, 4, 1374. [Google Scholar] [CrossRef] [PubMed]
- Diederich, F.; Kivala, M. All-Carbon Scaffolds by Rational Design. Adv. Mater. 2010, 22, 803–812. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Zhang, H.; Shi, D.; Sun, J.; Du, S.; Liu, F.; Gao, H.J. Highly Ordered, Millimeter-Scale, Continuous, Single-Crystalline Graphene Monolayer Formed on Ru (0001). Adv. Mater. 2009, 21, 2777–2780. [Google Scholar] [CrossRef]
- Min, S.K.; Kim, W.Y.; Cho, Y.; Kim, K.S. Fast DNA Sequencing with a Graphene-Based Nanochannel Device. Nat. Nanotechnol. 2011, 6, 162–165. [Google Scholar] [CrossRef] [PubMed]
- Cervetti, C.; Rettori, A.; Pini, M.G.; Cornia, A.; Repollés, A.; Luis, F.; Dressel, M.; Rauschenbach, S.; Kern, K.; Burghard, M. The Classical and Quantum Dynamics of Molecular Spins on Graphene. Nat. Mater. 2016, 15, 164–168. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.; Jiang, D.; Katsnelson, M.; Grigorieva, I.; Dubonos, S.; Firsov, A.A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novoselov, K.S.; McCann, E.; Morozov, S.; Fal’ko, V.I.; Katsnelson, M.; Zeitler, U.; Jiang, D.; Schedin, F.; Geim, A. Unconventional Quantum Hall Effect and Berry’s Phase of 2π in Bilayer Graphene. Nat. Phys. 2006, 2, 177–180. [Google Scholar] [CrossRef] [Green Version]
- Cocq, K.; Saffon-Merceron, N.; Coppel, Y.; Poidevin, C.; Maraval, V.; Chauvin, R. Carbo-Naphthalene: A Polycyclic Carbo-Benzenoid Fragment of A-Graphyne. Angew. Chem. Int. Ed. 2016, 128, 15357–15360. [Google Scholar] [CrossRef]
- Malko, D.; Neiss, C.; Görling, A. Two-Dimensional Materials with Dirac Cones: Graphynes Containing Heteroatoms. Phys. Rev. B 2012, 86, 045443. [Google Scholar] [CrossRef]
- Puigdollers, A.R.; Alonso, G.; Gamallo, P. First-Principles Study of Structural, Elastic and Electronic Properties of Α-, Β- and Γ-Graphyne. Carbon 2016, 96, 879–887. [Google Scholar] [CrossRef]
- Chen, J.; Xi, J.; Wang, D.; Shuai, Z. Carrier Mobility in Graphyne Should Be Even Larger Than That in Graphene: A Theoretical Prediction. J. Phys. Chem. Lett. 2013, 4, 1443–1448. [Google Scholar] [CrossRef] [PubMed]
- Sevinçli, H.; Sevik, C. Electronic, Phononic, and Thermoelectric Properties of Graphyne Sheets. Appl. Phys. Lett. 2014, 105, 223108. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, J.; Li, Z.; Zhao, R.; Tong, L.; Liu, Z.; Zhang, J.; Liu, Z. Raman Spectra and Corresponding Strain Effects in Graphyne and Graphdiyne. J. Phys. Chem. C 2016, 120, 10605–10613. [Google Scholar] [CrossRef]
- Srinivasu, K.; Ghosh, S.K. Graphyne and Graphdiyne: Promising Materials for Nanoelectronics and Energy Storage Applications. J. Phys. Chem. C 2012, 116, 5951–5956. [Google Scholar] [CrossRef]
- Long, M.; Tang, L.; Wang, D.; Li, Y.; Shuai, Z. Electronic Structure and Carrier Mobility in Graphdiyne Sheet and Nanoribbons: Theoretical Predictions. ACS Nano 2011, 5, 2593–2600. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, L.; Liu, H.; Li, Y. Graphdiyne and Graphyne: From Theoretical Predictions to Practical Construction. Chem. Soc. Rev. 2014, 43, 2572–2586. [Google Scholar] [CrossRef] [PubMed]
- Malko, D.; Neiss, C.; Viñes, F.; Görling, A. Competition for Graphene: Graphynes with Direction-Dependent Dirac Cones. Phys. Rev. Lett. 2012, 108, 086804. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Li, Y.; Qian, X.; Liu, H.; Lin, H.; Chen, N.; Li, Y. Construction of Tubular Molecule Aggregations of Graphdiyne for Highly Efficient Field Emission. J. Phys. Chem. C 2011, 115, 2611–2615. [Google Scholar] [CrossRef]
- Zhou, J.; Lv, K.; Wang, Q.; Chen, X.; Sun, Q.; Jena, P. Electronic Structures and Bonding of Graphyne Sheet and Its Bn Analog. J. Chem. Phys. 2011, 134, 174701. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Zhang, L.; Song, B.; Du, S.; Gao, H.-J. Graphyne- and Graphdiyne-Based Nanoribbons: Density Functional Theory Calculations of Electronic Structures. Appl. Phys. Lett. 2011, 98, 173102. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, M.; He, X.; Wang, Z.; Zhang, X.; Liu, X. High Mobility and High Storage Capacity of Lithium in sp–sp2 Hybridized Carbon Network: The Case of Graphyne. J. Phys. Chem. C 2011, 115, 8845–8850. [Google Scholar] [CrossRef]
- Xu, Z.; Lv, X.; Li, J.; Chen, J.; Liu, Q. A Promising Anode Material for Sodium-Ion Battery with High Capacity and High Diffusion Ability: Graphyne and Graphdiyne. RSC Adv. 2016, 6, 25594–25600. [Google Scholar] [CrossRef]
- Yue, Q.; Chang, S.; Kang, J.; Tan, J.; Qin, S.; Li, J. Magnetic and Electronic Properties of Α-Graphyne Nanoribbons. J. Chem. Phys. 2012, 136, 244702. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Liu, Z.; Gao, W.; Zheng, Y. Electronic Properties of Four Typical Zigzag-Edged Graphyne Nanoribbons. J. Phys. Condens. Matter 2013, 25, 285502. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Guo, W.; Zeng, X.C. Intrinsic Electronic and Transport Properties of Graphyne Sheets and Nanoribbons. Nanoscale 2013, 5, 9264–9276. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.Q. Size Dependence of Nanostructures: Impact of Bond Order Deficiency. Prog. Solid State Chem. 2007, 35, 1–159. [Google Scholar] [CrossRef]
- Sun, C.Q. Relaxation of the Chemical Bond. Springer Ser. Chem. Phys. 2014, 108, 807. [Google Scholar]
- Zhang, X.; Wang, S.; Liu, Y.; Li, L.; Sun, C. Catalytic Enhancement of Gold Nanocages Induced by Undercoordination-Charge-Polarization. APL Mater. 2017, 5, 053501. [Google Scholar] [CrossRef]
- Liu, X.; Bo, M.; Zhang, X.; Li, L.; Nie, Y.; TIan, H.; Sun, Y.; Xu, S.; Wang, Y.; Zheng, W. Coordination-Resolved Electron Spectrometrics. Chem. Rev. 2015, 115, 6746–6810. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.Q.; Pan, L.; Fu, Y.Q.; Tay, B.K.; Li, S. Size Dependence of the 2p-Level Shift of Nanosolid Silicon. J. Phys. Chem. B 2003, 107, 5113–5115. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, X.; Bo, M.; Zhang, X.; Liu, X.; Sun, C.Q.; Huang, Y. Number-of-Layer, Pressure, and Temperature Resolved Bond-Phonon-Photon Cooperative Relaxation of Layered Black Phosphorus. J. Raman Spectrosc. 2016, 47, 1304–1309. [Google Scholar] [CrossRef]
- Pauling, L. Atomic Radii and Interatomic Distances in Metals. J. Am. Chem. Soc. 1947, 69, 542–553. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. Krystallbau und Chemische Zusammensetzung. Ber. Dtsch. Chem. Ges. 1927, 60, 1263–1296. [Google Scholar] [CrossRef]
- Kröger, F.; Vink, H.; Seitz, F.; Turnbull, D. Solid State Physics; Academic Press: New York, NY, USA, 1956; Volume 3, p. 307. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Narita, N.; Nagai, S.; Suzuki, S.; Nakao, K. Optimized Geometries and Electronic Structures of Graphyne and Its Family. Phys. Rev. B 1998, 58, 11009. [Google Scholar] [CrossRef]
- Kang, J.; Li, J.; Wu, F.; Li, S.-S.; Xia, J.-B. Elastic, Electronic, and Optical Properties of Two-Dimensional Graphyne Sheet. J. Phys. Chem. C 2011, 115, 20466–20470. [Google Scholar] [CrossRef]








| Stimuli | Aα-GYNRs | Zα-GYNRs | Aβ-GYNRs | Zβ-GYNRs |
|---|---|---|---|---|
| N = 1 | 1.55 | 2.66 | 0.92 | 0.00 |
| N = 2 | 1.29 | 1.72 | 0.54 | 0.00 |
| N = 3 | 1.01 | 1.24 | 0.44 | 0.00 |
| N = 4 | 0.88 | 0.84 | 0.31 | 0.00 |
| N = 5 | 0.76 | 0.73 | 0.17 | 0.00 |
| N = 6 | 0.69 | 0.64 | 0.11 | 0.00 |
| bulk | 0.51 | 0.00 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Bo, M.; Sun, C.Q.; Huang, Y. The Band-Gap Modulation of Graphyne Nanoribbons by Edge Quantum Entrapment. Nanomaterials 2018, 8, 92. https://doi.org/10.3390/nano8020092
Liu Y, Bo M, Sun CQ, Huang Y. The Band-Gap Modulation of Graphyne Nanoribbons by Edge Quantum Entrapment. Nanomaterials. 2018; 8(2):92. https://doi.org/10.3390/nano8020092
Chicago/Turabian StyleLiu, Yonghui, Maolin Bo, Chang Qing Sun, and Yongli Huang. 2018. "The Band-Gap Modulation of Graphyne Nanoribbons by Edge Quantum Entrapment" Nanomaterials 8, no. 2: 92. https://doi.org/10.3390/nano8020092
APA StyleLiu, Y., Bo, M., Sun, C. Q., & Huang, Y. (2018). The Band-Gap Modulation of Graphyne Nanoribbons by Edge Quantum Entrapment. Nanomaterials, 8(2), 92. https://doi.org/10.3390/nano8020092