Nature of Excitons in Bidimensional WSe2 by Hybrid Density Functional Theory Calculations
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Atomic and Electronic Structure of 2D-WSe2 by Hybrid Density Functional Calculations
3.2. Self-Trapped Charge Carriers in WSe2
3.2.1. Self-Trapped Electron
3.2.2. Self-Trapped Hole
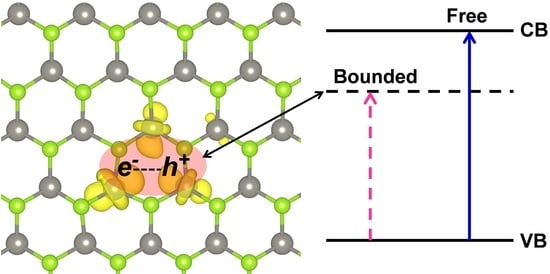
3.3. Self-Trapped Exciton in WSe2
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Wilson, A.D.; Yoffe, J.A. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 1969, 18, 193–335. [Google Scholar] [CrossRef]
- Bromley, R.A.; Murray, R.B.; Yoffe, A.D. The band structures of some transition metal dichalcogenides. III. Group VIA: Trigonal prism materials. J. Phys. C Solid Stat. Phys. 1972, 5, 759. [Google Scholar] [CrossRef]
- Dickinson, R.G.; Pauling, L. The crystal structure of molybdenite. J. Am. Chem. Soc. 1923, 45, 1466–1471. [Google Scholar] [CrossRef]
- Kolobov, A.V.; Tominaga, J. Two-Dimensional Transition Metal Dichalcogenides; Springer: Basel, Switzerland, 2016. [Google Scholar]
- Liu, G.B.; Xiao, D.; Yao, Y.; Xu, X.; Yao, W. Electronic structure and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides. Chem. Soc. Rev. 2015, 44, 2643–2663. [Google Scholar] [CrossRef] [PubMed]
- Chhowalla, M.; Shin, H.S.; Eda, G.; Li, L.; Loh, K.P.; Zhang, H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263–275. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Qiao, X.; Liu, X.; Tan, P.; Zhang, X. Photoluminescence properties and excitation dynamics in monolayer WSe2. Appl. Phys. Lett. 2014, 105, 101901. [Google Scholar] [CrossRef]
- Chernikov, A.; Berkelbach, T.C.; Hill, H.M.; Rigosi, A.; Li, Y.; Aslan, O.B.; Reichman, D.R.; Hybertsen, M.S.; Heinz, T.F. Exciton binding energy and nonhydrogenic rydberg series in monolayer WS2. Phys. Rev. Lett. 2014, 113, 076802. [Google Scholar] [CrossRef] [PubMed]
- Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 2012, 86, 115409. [Google Scholar] [CrossRef]
- Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
- Srivastava, A.; Sidler, M.; Allain, A.V.; Lembke, D.S.; Kis, A.; Imamoglu, A. Optically active quantum dots in monolayer WSe2. Nat. Nanotechnol. 2015, 10, 491–496. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, W.; Zhang, H.; Zhu, G.; Lee, S.; Lin, Z.; Wang, Z.L. Evolution of electronic structure in atomically thin sheets of WS2 and WSe2. ACS Nano 2013, 7, 791–797. [Google Scholar] [CrossRef] [PubMed]
- Ross, J.S.; Klement, P.; Jones, A.M.; Ghimire, N.J.; Yan, J.; Mandrus, D.G.; Taniguchi, T.; Watanabe, K.; Kitamura, K.; Yao, W.; et al. Electrically tunable excitonic light-emitting diodes based on monolayer WSe2 p-n junctions. Nat. Nanotechnol. 2014, 9, 268–272. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Kumar, N.; Zhao, L.; Wang, Z.; Mak, K.F.; Zhao, H.; Shan, J. Tightly Bound Excitons in Monolayer WSe2. Phys. Rev. Lett. 2014, 113, 026803. [Google Scholar] [CrossRef] [PubMed]
- Hanbicki, A.T.; Currie, M.; Kioseoglu, G.; Friedman, A.L.; Jonker, B.T. Measurement of high exciton binding energy in the monolayer transition-metal dichalcogenides WS2 and WSe2. Solid State Commun. 2015, 203, 16–20. [Google Scholar] [CrossRef]
- Kylänpää, I.; Komsa, H.P. Binding energies of exciton complexes in transition metal dichalcogenide monolayers and effect of dielectric environment. Phys. Rev. B 2015, 92, 205418. [Google Scholar] [CrossRef]
- Hsu, W.; Lu, L.; Wang, D.; Huang, J.; Li, M.; Chang, T.; Chou, Y.; Juang, Z.; Jeng, H.; Li, L.; et al. Evidence of indirect gap in monolayer WSe2. Nat. Commun. 2017, 8, 929. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Chen, Y.; Johnson, A.; Li, M.; Li, L.; Mende, P.C.; Feenstra, R.M.; Shih, C. Probing critical point energies of transition metal dichalcogenides: Surprising indirect gap of single layer WSe2. Nano Lett. 2015, 15, 6494–6500. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Wang, Y.; Ni, J.; Shi, L.; Shi, S.; Tang, W. First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M = Mo, Nb, W, Ta; X = S, Se, Te) monolayers. Phys. B 2011, 406, 2254–2260. [Google Scholar] [CrossRef]
- Rasmussen, F.A.; Thygesen, K.S. Computational 2D Materials Database: Electronic Structure of Transition-Metal Dichalcogenides and Oxides. J. Phys. Chem. C 2015, 119, 13169–13183. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, H.L.; Hennig, R.G. Computational Search for Single-Layer Transition-Metal Dichalcogenide Photocatalysts. J. Phys. Chem. C 2013, 117, 20440–20445. [Google Scholar] [CrossRef]
- Tonndorf, P.; Schmidt, R.; Böttger, P.; Zhang, X.; Börner, J.; Liebig, A.; Albrecht, M.; Kloc, C.; Gordan, O.; Zahn, D.R.T.; et al. Photoluminescence emission and raman response of monolayer MoS2, MoSe2 and WSe2. Opt. Express 2013, 21, 4908–4916. [Google Scholar] [CrossRef] [PubMed]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943. [Google Scholar] [CrossRef]
- Anisimov, V.I.; Solovyev, I.V.; Korotin, M.A.; Czyżyk, M.T.; Sawatzky, G.A. Density-functional theory and NiO photoemission spectra. Phys. Rev. B 1993, 48, 16929. [Google Scholar] [CrossRef]
- Liechtenstein, A.I.; Anisimov, V.I.; Zaanen, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. Electron Correlation in Semiconductors and Insulators: Band Gaps and Quasiparticle Energies. Phys. Rev. B Condens. Matter Mater. Phys. 1986, 34, 5390–5413. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997. [Google Scholar] [CrossRef]
- Turkowski, V.; Ud Din, N.; Rahman, T.S. Time-dependent density-functional theory and excitons in bulk and two-dimensional semiconductors. Computation 2017, 5, 39. [Google Scholar] [CrossRef]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601. [Google Scholar] [CrossRef]
- Botti, S.; Schindlmayr, A.; Del Sole, R.; Reining, L. Time-dependent density-functional theory for extended systems. Rep. Prog. Phys. 2007, 70, 357. [Google Scholar] [CrossRef]
- Di Valentin, C.; Selloni, A. Bulk and Surface Polarons in Photoexcited Anatase TiO2. J. Phys. Chem. Lett. 2011, 2, 2223–2228. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207. [Google Scholar] [CrossRef]
- Dovesi, R.; Orlando, R.; Erba, A.; Zicovich-Wilson, C.M.; Civalleri, B.; Casassa, S.; Maschio, L.; Ferrabone, M.; De La Pierre, M.; D’Arco, P.; et al. CRYSTAL14: A Program for the Ab Initio Investigation of Crystalline Solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL14 User’s Manual; University of Torino: Torino, Italy, 2014. [Google Scholar]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A Modular and Open-source Software Project for Quantum Simulations of Materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Hay, P.J.; Wadt, W.R. Ab Initio Effective Core Potentials for Molecular Calculations. Potentials for K to Au including the Outermost Core Orbitals. J. Chem. Phys. 1985, 82, 299. [Google Scholar] [CrossRef]
- Durand, P.H.; Barthelat, J.C. A Theoretical Method to Determine Atomic Pseudopotentials for Electronic Structure Calculations of Molecules and Solids. Theor. Chim. Acta 1975, 38, 283. [Google Scholar] [CrossRef]
- Wang, F.; Di Valentin, C.; Pacchioni, G. Electronic and Structural Properties of WO3: A Systematic Hybrid DFT Study. J. Phys. Chem. C 2011, 115, 8345–8353. [Google Scholar] [CrossRef]
- Heyd, J.; Peralta, J.E.; Scuseriaa, G.E. Energy Band Gaps and Lattice Parameters Evaluated with the Heyd-Scuseria-Ernzerh of Screened Hybrid Functional. J. Chem. Phys. 2005, 123, 174101. [Google Scholar] [CrossRef] [PubMed]
- Pernot, P.; Civalleri, B.; Presti, D.; Savin, A. Prediction Uncertainty of Density Functional Approximations for Properties of Crystals with Cubic Symmetry. J. Phys. Chem. A 2015, 119, 5288–5304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the Exchange Screening Parameter on the Performance of Screened Hybrid Functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 8, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation Energy Formula into a Functional of the Electron-Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic-Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Tanabe, I.; Gomez, M.; Coley, W.C.; Le, D.; Echeverria, E.M.; Stecklein, G.; Kandyba, V.; Balijepalli, S.K.; Klee, V.; Nguyen, A.E.; et al. Band structure characterization of WS2 grown by chemical vapor deposition. Appl. Phys. Lett. 2016, 108, 252103. [Google Scholar] [CrossRef] [Green Version]
- Kozawa, D.; Kumar, R.; Carvalho, A.; Amara, K.K.; Zhao, W.; Wang, S.; Toh, M.; Ribeiro, R.M.; Castro Neto, A.H.; Matsuda, K.; et al. Photocarrier relaxation pathway in two-dimensional semiconducting transition metal dichalcogenides. Nat. Commun. 2014, 5, 4543. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baugher, B.W.H.; Churchill, H.O.H.; Yang, Y.; Jarillo-Herrero, P. Optoelectronic devices based on electrically tunable p–n diodes in a monolayer dichalcogenide. Nat. Nanotechnol. 2014, 9, 262. [Google Scholar] [CrossRef] [PubMed]
- Klots, A.R.; Newaz, A.K.M.; Wang, B.; Prasai, D.; Krzyzanowska, H.; Lin, J.; Caudel, D.; Ghimire, N.J.; Yan, J.; Ivanov, B.L.; et al. Probing excitonic states in suspended two-dimensional semiconductors by photocurrent spectroscopy. Sci. Rep. 2014, 4, 6608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kosmider, K.; Fernandez-Rossier, J. Electronic properties of the MoS2-WS2 heterojunction. Phys. Rev. B 2013, 87, 075451. [Google Scholar] [CrossRef]
- Kormányos, A.; Burkard, G.; Gmitra, M.; Fabian, J.; Zolyomi, V.; Drummond, N.D.; Fal’ko, V. k•p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2015, 2, 022001. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Cheng, Y.C.; Schwingenschlogl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 2011, 84, 153402. [Google Scholar] [CrossRef]
- Wickramaratne, D.; Zahid, F.; Lake, R.K. Electronic and thermoelectric properties of few-layer transition metal dichalcogenides. J. Chem. Phys. 2014, 140, 124710. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuan, H.; Bahramy, M.S.; Morimoto, K.; Wu, S.; Nomura, K.; Yang, B.J.; Shimotani, H.; Suzuki, R.; Toh, M.; Kloc, C.; et al. Zeeman-type spin splitting controlled by an electric field. Nat. Phys. 2013, 9, 563–569. [Google Scholar] [CrossRef]
- Kang, J.; Tongay, S.; Zhou, J.; Li, J.; Wu, J. Band offsets and heterostructures of two-dimensional semiconductors. Appl. Phys. Lett. 2013, 102, 012111. [Google Scholar] [CrossRef]
- Van Ginhoven, R.M.; Jónsson, H.; René Corrales, L. Characterization of Exciton Self-trapping in Amorphous Silica. J. Non-Cryst. Solids 2006, 352, 2589–2595. [Google Scholar] [CrossRef]












| K Point | Main Contribution | Minor Contribution |
|---|---|---|
| KC | W- | Se-px, py |
| KV | W- | Se-px, py |
| QC | W- | W-; Se-px, py, pz |
| ΓV | W- | Se-pz |
| Supercell | Energy Parameters (eV) | Spin Density | |||
|---|---|---|---|---|---|
| ΔEABS | ΔEST | ΔEPL | ΔEDIST | ||
| 4 × 4 | 2.47 | −0.75 | −1.04 | 0.68 | 0.922 0.534 0.534 |
| 5 × 5 | 2.38 | −0.66 | −1.04 | 0.68 | 0.930 0.530 0.530 |
| 6 × 6 | 2.44 | −0.74 | −1.04 | 0.66 | 0.934 0.533 0.533 |
| 8 × 8 | 2.35 | −0.69 | −1.03 | 0.63 | 0.935 0.535 0.535 |
| Functional | Energy Parameters (eV) | |||
|---|---|---|---|---|
| ΔEABS | ΔEST | ΔEPL | ΔEDIST | |
| HSE06/CRY14 | 2.44 | −0.74 | −1.04 | 0.66 |
| B3LYP/CRY14 | 2.38 | −0.81 | −0.90 | 0.67 |
| PBE/CRY14 | 1.91 | −0.17 | −1.17 | 0.57 |
| PBE/QE | 1.71 | −0.19 | −1.30 | 0.22 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Lazzaroni, P.; Di Valentin, C. Nature of Excitons in Bidimensional WSe2 by Hybrid Density Functional Theory Calculations. Nanomaterials 2018, 8, 481. https://doi.org/10.3390/nano8070481
Liu H, Lazzaroni P, Di Valentin C. Nature of Excitons in Bidimensional WSe2 by Hybrid Density Functional Theory Calculations. Nanomaterials. 2018; 8(7):481. https://doi.org/10.3390/nano8070481
Chicago/Turabian StyleLiu, Hongsheng, Paolo Lazzaroni, and Cristiana Di Valentin. 2018. "Nature of Excitons in Bidimensional WSe2 by Hybrid Density Functional Theory Calculations" Nanomaterials 8, no. 7: 481. https://doi.org/10.3390/nano8070481
APA StyleLiu, H., Lazzaroni, P., & Di Valentin, C. (2018). Nature of Excitons in Bidimensional WSe2 by Hybrid Density Functional Theory Calculations. Nanomaterials, 8(7), 481. https://doi.org/10.3390/nano8070481