Effects of Angular Dependency of Particulate Light Scattering Intensity on Determination of Samples with Bimodal Size Distributions Using Dynamic Light Scattering Methods
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
2.2. DLS Measurements and Analysis
2.3. Asymmetric Flow Field-Flow Fractionation with Multi-Angle Light Scattering Measurements
3. Results and Discussion
3.1. DLS Measurements for Single Polystyrene Latex
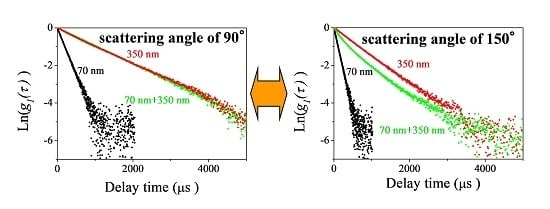
3.2. DLS Measurements for Mixtures of Two Differently Sized Polystyrene Latex
3.3. Determination of The Relative Concentration Ratios of Nanoparticles in Samples
3.4. Asymmetric Flow Field-Flow Fractionation Measurements for Mixtures of Two Differently Sized Polystyrene Latex
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Kaasalainen, M.; Aseyev, V.; Haartman, E.; Karaman, D.S.; Mäkilä, E.; Tenhu, H.; Rosenholm, J.; Salonen, J. Size, stability, and porosity of mesoporous nanoparticles characterized with light scattering. Nanoscale Res. Lett. 2017, 12, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Huang, B.; Zhou, T.; Liu, Y.; Shi, H. Aggregation behavior of engineered nanoparticles and their impact on activated sludge in wastewater treatment. Chemosphere 2015, 119, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Sahle, F.F.; Gerecke, C.; Kleuser, B.; Bodmeier, R. Formulation and comparative in vitro evaluation of various dexamethasone-loaded pH-sensitive polymeric nanoparticles intended for dermal applications. Int. J. Pharm. 2017, 516, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Zheng, T.; Bott, S.; Huo, Q.J. Techniques for accurate sizing of gold nanoparticles using dynamic light scattering with particular application to chemical and biological sensing based on aggregate formation. ACS Appl. Mater. Interfaces 2016, 8, 21585–21594. [Google Scholar] [CrossRef] [PubMed]
- Klitzke, S.; Metreveli, G.; Peters, A.; Schaumann, G.E.; Lang, F. The fate of silver nanoparticles in soil solution—Sorption of solutes and aggregation. Sci. Total Environ. 2014, 535, 54–60. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chen, H.; Du, X.; Wen, D. Photothermal conversion characteristics of gold nanoparticle dispersions. Sol. Energy 2014, 100, 141–147. [Google Scholar] [CrossRef] [Green Version]
- Jing, D.; Hu, Y.; Liu, M.; Wei, J.; Guo, L. Preparation of highly dispersed nanofluid and CFD study of its utilization in a concentrating PV/T system. Sol. Energy 2015, 112, 30–40. [Google Scholar] [CrossRef]
- Deloid, G.; Cohen, J.M.; Pygiotakis, G.; Demokritou, P. Preparation, characterization, and in vitro dosimetry of dispersed, engineered nanomaterials. Nat. Protoc. 2017, 12, 355–371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kato, H.; Nakamura, A.; Shimizu, M.; Banno, H.; Kezuka, Y.; Matsubara, K.; Hosoi, K.; Yoshida, S.; Fujimoto, T. Acceleration of dispersing calcium carbonate particle in aqueousmedia using jet milling method. Colloids Surf. A 2017, 520, 570–579. [Google Scholar] [CrossRef]
- Djurišić, A.B.; Leung, Y.H.; Ng, A.M.C.; Xu, X.Y.; Lee, P.K.H.; Degger, N.; Wu, R.S.S. Toxicity of Metal Oxide Nanoparticles: Mechanisms, Characterization, and Avoiding Experimental Artefacts. Small 2015, 11, 26–44. [Google Scholar] [CrossRef] [PubMed]
- Kato, H.; Suzuki, M.; Fujita, K.; Horie, M.; Endoh, S.; Yoshida, Y.; Iwahashi, H.; Takahashi, K.; Nakamura, A.; Kinugasa, S. Reliable size determination of nanoparticles using dynamic light scattering method for in vitro toxicology assessment. Toxicol. In Vitro 2009, 23, 927–934. [Google Scholar] [CrossRef] [PubMed]
- Berne, B.J.; Pecora, R. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics; Wiley: Hoboken, NJ, USA, 1976. [Google Scholar]
- International Organization for Standardization (ISO). Particle Size Analysis–Dynamic Light Scattering (DLS); ISO 22412; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- Kato, H.; Nakamura, A.; Oouchi, N.; Kinugasa, S. Determination of bimodal size distribution using dynamic light scattering methods in the submicrometer size range. Mater. Express 2016, 6, 175–184. [Google Scholar] [CrossRef]
- Kato, H.; Nakamura, A.; Takahashi, K.; Kinugasa, S. Accurate Size and Size-Distribution Determination of Polystyrene Latex Nanoparticles in Aqueous Medium Using Dynamic Light Scattering and Asymmetrical Flow Field Flow Fractionation with Multi-Angle Light Scattering. Nanomaterials 2012, 2, 15–30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kato, H.; Nakamura, A.; Noda, N. Determination of Size Distribution of Silica Nanoparticles: A Comparison of Scanning Electron Microscopy, Dynamic Light Scattering, and Flow Field-Flow Fractionation with Multiangle Light Scattering Methods. Mater. Express 2014, 4, 144–152. [Google Scholar] [CrossRef]
- Mie, G. Sättigungsstrom und Stromkurve einer schlecht leitenden Flüssigkeit. Ann. Phys. 1908, 331, 597–614. [Google Scholar] [CrossRef]
- Bantle, S.; Schmidt, M.; Burchard, W. Simultaneous static and dynamic light scattering. Macromolecules 1982, 15, 1604–1609. [Google Scholar] [CrossRef]
- Wenzel, M.; Burchard, W.; Schätzel, K. Dynamic light scattering from semidilute cellulose-tri-carbanilate solutions. Polymer 1986, 27, 195–201. [Google Scholar] [CrossRef]
- Miles, R.B.; Lempert, W.R.; Forkey, J.N. Laser rayleigh scattering. Meas. Sci. Technol. 2001, 12, 33–51. [Google Scholar] [CrossRef]
- Schimpf, M.; Caldwell, K.J.C. Giddings Field-Flow Fractionation Handbook; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- International Organization for Standardization (ISO). Nanotechnologies-Analysis of Nano-Objects Using Asymmetrical-Flow and Centrifugal Field-Flow Fractionation; ISO/TS 21362; ISO: Geneva, Switzerland, 2018. [Google Scholar]
- Kato, H.; Nakamura, A.; Banno, H.; Shimizu, M. Separation of different-sized silica nanoparticles using asymmetric flow field-flow fractionation by control of the Debye length of the particles with the addition of electrolyte molecules. Colloids Surf. A 2018, 538, 678–685. [Google Scholar] [CrossRef]











| Sample Name | Official Diameter (a) | Official CV Value (b) |
|---|---|---|
| (nm) | % | |
| W15BG001 | 70 | 6.1 |
| W2KS150 | 156 | 6.3 |
| W2KS200 | 210 | 4.7 |
| W16E303 | 350 | 5.1 |
| W15E182 | 500 | 5.0 |
| Sample Name | Sample | Sample |
|---|---|---|
| Relative Ratio of W15BG001 | Relative Ratio of W2KS150 | |
| 70-150-1 | 2 | 1 |
| 70-150-2 | 1 | 1 |
| 70-150-3 | 1 | 2 |
| 70-210-1 | 2 | 1 |
| 70-210-2 | 1 | 1 |
| 70-210-3 | 1 | 2 |
| 70-350-1 | 2 | 1 |
| 70-350-2 | 1 | 1 |
| 70-350-3 | 1 | 2 |
| 70-500-1 | 2 | 1 |
| 70-500-2 | 1 | 1 |
| 70-500-3 | 1 | 2 |
| Sample Name | Observed Angle (°) | |||
|---|---|---|---|---|
| 60 | 90 | 120 | 150 | |
| 70-350-1 | − | − | 67 ± 6 | 67 ± 3 |
| 70-350-2 | − | − | 50 ± 5 | 50 ± 3 |
| 70-350-3 | − | − | 33 ± 6 | 33 ± 3 |
| 70-500-1 | − | 67 ± 10 | 67 ± 5 | 67 ± 2 |
| 70-500-2 | − | 50 ± 9 | 50 ± 5 | 50 ± 2 |
| 70-500-3 | − | 33 ± 9 | 33 ± 6 | 33 ± 3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kato, H.; Nakamura, A.; Kinugasa, S. Effects of Angular Dependency of Particulate Light Scattering Intensity on Determination of Samples with Bimodal Size Distributions Using Dynamic Light Scattering Methods. Nanomaterials 2018, 8, 708. https://doi.org/10.3390/nano8090708
Kato H, Nakamura A, Kinugasa S. Effects of Angular Dependency of Particulate Light Scattering Intensity on Determination of Samples with Bimodal Size Distributions Using Dynamic Light Scattering Methods. Nanomaterials. 2018; 8(9):708. https://doi.org/10.3390/nano8090708
Chicago/Turabian StyleKato, Haruhisa, Ayako Nakamura, and Shinichi Kinugasa. 2018. "Effects of Angular Dependency of Particulate Light Scattering Intensity on Determination of Samples with Bimodal Size Distributions Using Dynamic Light Scattering Methods" Nanomaterials 8, no. 9: 708. https://doi.org/10.3390/nano8090708
APA StyleKato, H., Nakamura, A., & Kinugasa, S. (2018). Effects of Angular Dependency of Particulate Light Scattering Intensity on Determination of Samples with Bimodal Size Distributions Using Dynamic Light Scattering Methods. Nanomaterials, 8(9), 708. https://doi.org/10.3390/nano8090708