Stability of Coinage Metals Interacting with C60
Abstract
:1. Introduction
2. Computational Methods
3. Results
3.1. Initial Configurations
3.2. Validation of the Pseudopotentials and Basis Sets
3.2.1. Calculation on Band Gap of a C60 Molecule
3.2.2. Calculations of Energy Minimisation on Bulk Cu, Ag and Au
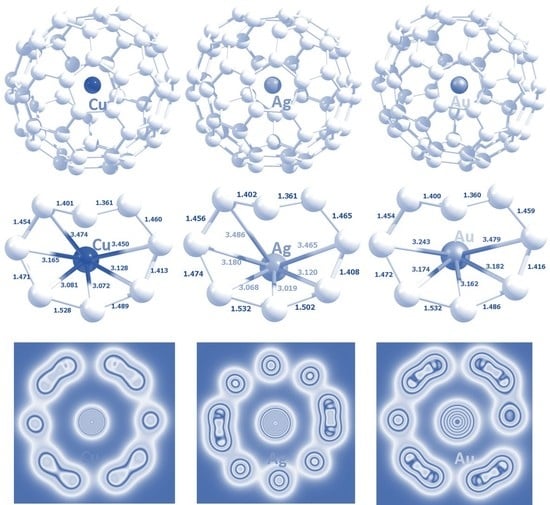
3.3. Encapsulation of Coinage Metals within C60
3.4. Adsorption of Coinage Metals on the Surface of C60
3.5. Defective C60 Structure
3.6. Encapsulation of Metal Atoms within a Defective C60 Molecule
3.7. Adsorption of Metal Atoms on the Surface of Defective C60 Molecule
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kroto, H.W.; Allaf, A.W.; Balm, S.P. C60: Buckminsterfullerene. Chem. Rev. 1991, 91, 1213–1235. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral Fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef]
- Acquah, S.; Penkova, A.V.; Markelov, D.; Semisalova, A.S.; Leonhardt, B.E.; Magi, J.M. Review—The Beautiful Molecule: 30 Years of C60 and Its Derivatives. ECS J. Solid State Sci. Technol. 2017, 6, M3155–M3162. [Google Scholar]
- Bühl, M.; Hirsch, A. Spherical Aromaticity of Fullerenes. Chem. Rev. 2001, 101, 1153–1184. [Google Scholar] [CrossRef] [PubMed]
- Dresselhaus, M.S.; Dresslhaus, G. Fullerenes and Fullerene Derived Solids as Electronic Materials. Annu. Rev. Mater. Sci. 1995, 25, 487–523. [Google Scholar] [CrossRef]
- Bakry, R.; Vallant, R.M.; Najam-ul-Haq, M.; Rainer, M.; Szabo, Z.; Huck, C.W.; Bonn, G.K. Medicinal applications of fullerenes. Int. J. Nanomed. 2007, 2, 639–649. [Google Scholar]
- Goodarzi, S.; Da Ros, T.; Conde, J.; Sefat, F.; Mozafari, M. Fullerene: Biomedical engineers get to revisit an old friend. Mater. Today 2017, 20, 460–480. [Google Scholar] [CrossRef]
- Kroto, H.W. C60: Buckminsterfullerene, The Celestial Sphere that Fell to Earth. Angew. Chem. Int. Ed. Engl. 1992, 31, 111–129. [Google Scholar] [CrossRef]
- He, T.; Gao, G.; Kou, L.; Will, G.; Du, A. Endohedral metallofullerenes (M@C60) as efficient catalysts for highly active hydrogen evolution reaction. J. Catal. 2017, 354, 231–235. [Google Scholar] [CrossRef]
- Mahdy, A.M.E. DFT study of hydrogen storage in Pd-decorated C60 fullerene. Mol. Phys. 2015, 113, 3531–3544. [Google Scholar] [CrossRef]
- Tawfik, S.A.; Cui, X.Y.; Ringer, S.P.; Stampfl, C. Endohedral metallofullerenes, M@C60 (M = Ca, Na, Sr): Selective adsorption and sensing of open-shell NOx gases. Phys. Chem. Chem. Phys. 2016, 18, 21315–21321. [Google Scholar] [CrossRef] [PubMed]
- Klingeler, R.; Kann, G.; Wirth, I.; Eisebitt, S.; Bechthold, P.S.; Neeb, M.; Eberhardt, W. La@C60: A metallic endohedral fullerene. J. Chem. Phys. 2001, 115, 7215–7218. [Google Scholar] [CrossRef]
- Cho, S.C.; Kaneko, T.; Ishida, H.; Hatakeyama, R. Nitrogen-atom endohedral fullerene synthesis with high efficiency by controlling plasma-ion irradiation energy and C60 internal energy. J. Appl. Phys. 2015, 117, 123301. [Google Scholar] [CrossRef]
- Ohtsuki, T.; Masumoto, K.; Ohno, K.; Maruyma, Y.; Kawazoe, Y.; Sueki, K.; Kikuchi, K. Insertion of Be Atoms in C60 Fullerene Cages: Be@C60. Phys. Rev. Lett. 1996, 77, 3522–3524. [Google Scholar] [CrossRef]
- Kuganathan, N.; Green, J.C.; Himmel, H.-J. Dinitrogen fixation and activation by Ti and Zr atoms, clusters and complexes. New J. Chem. 2006, 30, 1253–1262. [Google Scholar] [CrossRef]
- Kyesmen, P.I.; Onoja, A.; Amah, A.N. Fullerenes synthesis by combined resistive heating and arc discharge techniques. Springerplus 2016, 5, 1323. [Google Scholar] [CrossRef]
- Saha, S.K.; Chowdhury, D.P.; Das, S.K.; Guin, R. Encapsulation of radioactive isotopes into C60 fullerene cage by recoil implantation technique. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2006, 243, 277–281. [Google Scholar] [CrossRef]
- Wan, Z.; Christian, J.F.; Anderson, S.L. Collision of Li+ and Na+ with C60: Insertion, fragmentation, and thermionic emission. Phys. Rev. Lett. 1992, 69, 1352–1355. [Google Scholar] [CrossRef]
- Saunders, M.; Cross, R.J.; Jiménez-Vázquez, H.A.; Shimshi, R.; Khong, A. Noble gas atoms inside fullerenes. Science 1996, 271, 1693–1697. [Google Scholar] [CrossRef]
- Braun, T.; Rausch, H. Endohedral incorporation of argon atoms into C60 by neutron irradiation. Chem. Phys. Lett. 1995, 237, 443–447. [Google Scholar] [CrossRef]
- Brocławik, E.; Eilmes, A. Density functional study of endohedral complexes M@C60 (M=Li, Na, K, Be, Mg, Ca, La, B, Al): Electronic properties, ionization potentials, and electron affinities. J. Chem. Phys. 1998, 108, 3498–3503. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Pandey, S.K.; Misra, N. Encapsulation of lawrencium into C60 fullerene: Lr@C60 versus Li@C60. Mater. Chem. Phys. 2016, 177, 437–441. [Google Scholar] [CrossRef]
- Wang, Y.; Tománek, D.; Ruoff, R.S. Stability of M@C60 endohedral complexes. Chem. Phys. Lett. 1993, 208, 79–85. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, X.; Zhao, X. Electronic structures of endohedral N@C60, O@C60 and F@C60. Chem. Phys. Lett. 1999, 312, 85–90. [Google Scholar] [CrossRef]
- Kuganathan, N.; Arya, A.K.; Rushton, M.J.D.; Grimes, R.W. Trapping of volatile fission products by C60. Carbon 2018, 132, 477–485. [Google Scholar] [CrossRef]
- Breton, J.; Gonzalez-Platas, J.; Girardet, C. Endohedral and exohedral adsorption in C60: An analytical model. J. Chem. Phys. 1993, 99, 4036–4040. [Google Scholar] [CrossRef]
- Yekymov, E.; Bounioux, C.; Itzhak-Cohen, R.; Zeiri, L.; Shahnazaryan, E.; Katz, E.A.; Yerushalmi-Rozen, R. All carbon non-covalent exohedral hybrids: C60 aggregates on nanotube networks. J. Energy Chem. 2018, 27, 957–961. [Google Scholar] [CrossRef]
- Nakamura, Y.; Kato, S.-I. Exohedral functionalization of fullerenes and supramolecular chemistry. Chem. Rec. 2011, 11, 77–94. [Google Scholar] [CrossRef]
- Sankar De, D.; Flores-Livas, J.A.; Saha, S.; Genovese, L.; Goedecker, S. Stable structures of exohedrally decorated C60-fullerenes. Carbon 2018, 129, 847–853. [Google Scholar] [CrossRef]
- Özdamar, B.; Boero, M.; Massobrio, C.; Felder-Flesch, D.; Roux, S.L. Exohedral M–C60 and M2–C60 (M = Pt, Pd) systems as tunable-gap building blocks for nanoarchitecture and nanocatalysis. J. Chem. Phys. 2015, 143, 114308. [Google Scholar] [CrossRef]
- Kobayashi, T.; Yokoyama, K. Theoretical study of the adsorption of Cs, Cs+, I, I−, and CsI on C60 fullerene. J. Nucl. Sci. Technol. 2016, 53, 1489–1493. [Google Scholar] [CrossRef]
- Suzumura, J.-i.; Hosoya, N.; Nagao, S.; Mitsui, M.; Nakajima, A. Electronic structures of exohedral lanthanide-C60 clusters. J. Chem. Phys. 2004, 121, 2649–2654. [Google Scholar] [CrossRef] [PubMed]
- Kuganathan, N.; Selvanantharajah, N.; Iyngaran, P.; Abiman, P.; Chroneos, A. Cadmium trapping by C60 and B-, Si-, and N-doped C60. J. Appl. Phys. 2019, 125, 054302. [Google Scholar] [CrossRef]
- Huang, H.; Ata, M.; Yoshimoto, Y. Cu@C60 formation in rf-plasma and ring-current induced magnetism of C60. Chem. Commun. 2004, 10, 1206–1207. [Google Scholar] [CrossRef]
- Narwade, S.S.; Mulik, B.B.; Mali, S.M.; Sathe, B.R. Silver nanoparticles sensitized C60(Ag@C60) as efficient electrocatalysts for hydrazine oxidation: Implication for hydrogen generation reaction. Appl. Surf. Sci. 2017, 396, 939–944. [Google Scholar] [CrossRef]
- Singhal, R.; Sharma, P.; Vishnoi, R.; Avasthi, D.K. Synthesis and characterizations of Au-C60 nanocomposite. J. Alloys Compd. 2017, 696, 9–15. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; p. 994. [Google Scholar]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, J.M. Osmylation of C60: Proof and characterization of the soccer-ball framework. Acc. Chem. Res. 1992, 25, 150–156. [Google Scholar] [CrossRef]
- Goclon, J.; Winkler, K.; Margraf, J.T. Theoretical investigation of interactions between palladium and fullerene in polymer. RSC Adv. 2017, 7, 2202–2210. [Google Scholar] [CrossRef] [Green Version]
- Marini, A.; Onida, G.; Del Sole, R. Quasiparticle Electronic Structure of Copper in the GW Approximation. Phys. Rev. Lett. 2001, 88, 016403. [Google Scholar] [CrossRef] [PubMed]
- Goraus, J.; Ślebarski, A.; Fijałkowski, M. Electronic structure of CeAgGa based on the experimental and model data. Phys. Status Solidi (B) 2011, 248, 2857–2863. [Google Scholar] [CrossRef]
- Haas, P.; Tran, F.; Blaha, P. Calculation of the lattice constant of solids with semilocal functionals. Phys. Rev. B 2009, 79, 085104. [Google Scholar] [CrossRef] [Green Version]
- Janthon, P.; Luo, S.; Kozlov, S.M.; Viñes, F.; Limtrakul, J.; Truhlar, D.G.; Illas, F. Bulk Properties of Transition Metals: A Challenge for the Design of Universal Density Functionals. J. Chem. Theory Comput. 2014, 10, 3832–3839. [Google Scholar] [CrossRef] [Green Version]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Slater, J.C. Atomic Radii in Crystals. J. Chem. Phys. 1964, 41, 3199–3204. [Google Scholar] [CrossRef]
- Clementi, E.; Raimondi, D.L.; Reinhardt, W.P. Atomic Screening Constants from SCF Functions. II. Atoms with 37 to 86 Electrons. J. Chem. Phys. 1967, 47, 1300–1307. [Google Scholar] [CrossRef]
- Zoberbier, T.; Chamberlain, T.W.; Biskupek, J.; Kuganathan, N.; Eyhusen, S.; Bichoutskaia, E.; Kaiser, U.; Khlobystov, A.N. Interactions and Reactions of Transition Metal Clusters with the Interior of Single-Walled Carbon Nanotubes Imaged at the Atomic Scale. J. Am. Chem. Soc. 2012, 134, 3073–3079. [Google Scholar] [CrossRef] [Green Version]
- Tascón, J.M.D.; Bottani, E.J. Nitrogen Physisorption on Defective C60. J. Phys. Chem. B 2002, 106, 9522–9527. [Google Scholar] [CrossRef]
- Bai, H.; Ji, W.; Liu, X.; Wang, L.; Yuan, N.; Ji, Y. Doping the Buckminsterfullerene by Substitution: Density Functional Theory Studies of C59X (X = B, N, Al, Si, P, Ga, Ge, and As). J. Chem. 2013, 2013, 9. [Google Scholar] [CrossRef]
- Kuganathan, N.; Green, J.C. Mercury telluride crystals encapsulated within single walled carbon nanotubes: A density functional study. Int. J. Quantum Chem. 2008, 108, 797–807. [Google Scholar] [CrossRef]
- Kuganathan, N.; Green, J.C. Crystal structure of low-dimensional Cu(i) iodide: DFT prediction of cuprophilic interactions. Chem. Commun. 2008, 21, 2432–2434. [Google Scholar] [CrossRef] [PubMed]
- Bichoutskaia, E.; Liu, Z.; Kuganathan, N.; Faulques, E.; Suenaga, K.; Shannon, I.J.; Sloan, J. High-precision imaging of an encapsulated Lindqvist ion and correlation of its structure and symmetry with quantum chemical calculations. Nanoscale 2012, 4, 1190–1199. [Google Scholar] [CrossRef] [PubMed]









| Parameter | ||||||
|---|---|---|---|---|---|---|
| Lattice Constant (Å) | Cohesive Energy (eV) | |||||
| Cu | Ag | Au | Cu | Ag | Au | |
| Proposed method | 3.57 | 4.09 | 4.12 | 3.99 | 2.97 | 3.63 |
| Experiment | 3.59 [47] | 4.06 [47] | 4.06 [47] | 3.48 [48] | 2.94 [48] | 3.81 [48] |
| Other theory | 3.501–3.686 [48] | 4.046–4.321 [48] | 4.084–4.112 [48] | 2.54–4.42 [48] | 1.87–3.60 [48] | 2.23–3.86 [48] |
| System | Atomic Radius (Å) | Encapsulation Energy (eV) | Bader Charge |e| | Magnetic Moment (µ) | ||||
|---|---|---|---|---|---|---|---|---|
| Empirical [50] | Calculated [51] | DFT | DFT + D | DFT | DFT + D | DFT | DFT + D | |
| Cu@C60 | 1.35 | 1.45 | 0.13 | −0.58 | +0.1675 | +0.1672 | 1.0000 | 1.0000 |
| Ag@C60 | 1.60 | 1.65 | 0.32 | −0.36 | +0.1704 | +0.1701 | 0.9983 | 0.9983 |
| Au@C60 | 1.35 | 1.74 | 0.23 | −0.56 | +0.0956 | +0.0954 | 0.9985 | 0.9985 |
| Initial Configuration | Final Configuration and Relative Adsorption Energies (eV) | ||
|---|---|---|---|
| Cu | Ag | Au | |
| H | C (0.00) | H (0.33) | H (0.67) |
| P | P (0.47) | P (0.30) | P (0.69) |
| 66 | 66 (0.12) | C (0.00) | C (0.00) |
| 65 | 65 (0.02) | 65 (0.07) | C (0.00) |
| C | C (0.00) | C (0.00) | C (0.00) |
| System | Adsorption Energy (eV) | Bader Charge |e| | Magnetic Moment (µ) |
|---|---|---|---|
| Cu_C60 | −0.98 | +0.30 | 0.9711 |
| Ag_C60 | −0.50 | +0.24 | 0.9329 |
| Au_C60 | −0.89 | +0.32 | 0.9778 |
| System | Encapsulation Energy (eV) | Bader Charge |e| | Magnetic Moment (µ) |
|---|---|---|---|
| Cu@C60_defe | −0.56 | +0.27 | 1.000 |
| Ag@C60_defe | −0.43 | +0.49 | 1.000 |
| Au@C60_defe | −0.51 | +0.31 | 1.000 |
| System | Encapsulation Energy (eV) | Bader Charge |e| | Magnetic Moment (µ) |
|---|---|---|---|
| Cu_C60_defe | −0.61 | +0.70 | 0.8896 |
| Ag_C60_defe | −0.41 | +0.62 | 0.9012 |
| Au_C60_defe | −0.48 | +0.51 | 0.9414 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuganathan, N.; Srikaran, R.; Chroneos, A. Stability of Coinage Metals Interacting with C60. Nanomaterials 2019, 9, 1484. https://doi.org/10.3390/nano9101484
Kuganathan N, Srikaran R, Chroneos A. Stability of Coinage Metals Interacting with C60. Nanomaterials. 2019; 9(10):1484. https://doi.org/10.3390/nano9101484
Chicago/Turabian StyleKuganathan, Navaratnarajah, Ratnasothy Srikaran, and Alexander Chroneos. 2019. "Stability of Coinage Metals Interacting with C60" Nanomaterials 9, no. 10: 1484. https://doi.org/10.3390/nano9101484
APA StyleKuganathan, N., Srikaran, R., & Chroneos, A. (2019). Stability of Coinage Metals Interacting with C60. Nanomaterials, 9(10), 1484. https://doi.org/10.3390/nano9101484