Computational Modeling of Tensile Stress Effects on the Structure and Stability of Prototypical Covalent and Layered Materials
Abstract
:1. Introduction
2. Computational Details
2.1. Electronic Structure Calculations
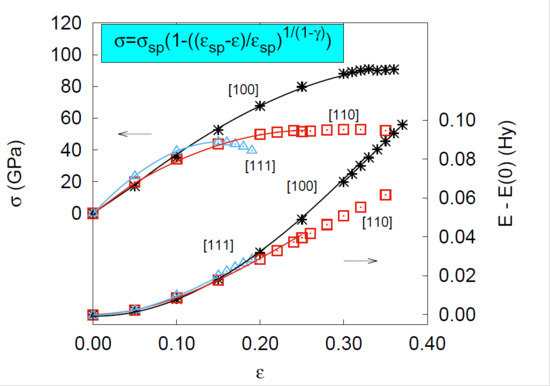
2.2. Spinodal-Like Stress–Strain Equation of State
2.3. Spinodal Equation of State Fittings
3. 3C-SiC, 2H-SiC, Graphite and 2H-MoS: Results and Discussion
3.1. Bulk Properties
3.2. Ideal Strength with and without Transverse Stress
Other Outcomes of the Stress–Strain SEOS: Energetics and Directional Young Moduli
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Asano, K.; Hayashi, T.; Takayama, D.; Sugawara, Y.; Ryu, S.H.; Palmour, J.W. Temperature dependence of On-state characteristics, and Switching characteristics of 5 kV class 4H-SiC SEJFET. IEEE Trans. Ind. Appl. 2005, 125, 147–152. [Google Scholar] [CrossRef] [Green Version]
- Peña-Álvarez, M.; del Corro, E.; Morales-García, Á.; Kavan, L.; Kalbac, M.; Frank, O. Single Layer Molybdenum Disulfide under Direct Out-of-Plane Compression: Low-Stress Band-Gap Engineering. Nano Lett. 2015, 15, 3139–3146. [Google Scholar] [CrossRef] [PubMed]
- Tsai, M.-L.; Su, S.-H.; Chang, J.-K.; Tsai, D.-S.; Chen, C.-H.; Wu, C.-I.; Li, L.-J.; Chen, L.-J.; He, J.-H. Monolayer MoS2 heterojunction solar cells. ACS Nano 2014, 8, 8317–8322. [Google Scholar] [CrossRef] [PubMed]
- Recio, J.M.; Menéndez, J.M.; Otero-de-la-Roza, A. (Eds.) An Introduction to High-Pressure Science and Technology; CRC-Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Radisavljevic, B.; Radenovic, A.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147–150. [Google Scholar] [CrossRef]
- Wang, H.; Yu, L.; Lee, Y.H.; Shi, Y.; Hsu, A.; Chin, M.L.; Li, L.J.; Dubey, M.; Kong, J.; Palacios, T. Integrated circuits based on bilayer MoS2 transistors. Nano Lett. 2012, 12, 4674–4680. [Google Scholar] [CrossRef]
- Fiori, G.; Szafranek, B.N.; Iannaccone, G.; Neumaier, D. Velocity saturation in few-layer MoS2 transistor. Appl. Phys. Lett. 2013, 103, 233509(1)–233509(4). [Google Scholar] [CrossRef]
- Kim, S.; Konar, A.; Hwang, W.S.; Lee, J.H.; Yang, J.; Jung, C.; Kim, H.; Yoo, J.B.; Choi, J.Y. High-mobility and low-power thin-film transistors based on multilayer MoS2 crystals. Nat. Commun. 2012, 3, 1011–1017. [Google Scholar] [CrossRef]
- Bollmann, W.; Spreadborough, J. Action of Graphite as a Lubricant. Nature 1960, 186, 29–30. [Google Scholar] [CrossRef]
- Peelaers, H.; Van de Walle, C.G. Elastic Constants and Pessure-Induced Effects in MoS2. J. Phys. Chem. 2014, 118, 12073–12076. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140A, 1133–1138. [Google Scholar] [CrossRef]
- Argaman, N.; Markov, G. Density functional theory: An introduction. Am. J. Phys. 2000, 68, 69–79. [Google Scholar] [CrossRef] [Green Version]
- Umeno, Y.; Kitamura, T. Ab Initio Simulation on Ideal Shear Strength of Silicon. Mater. Sci. Eng. 2002, 88, 79–84. [Google Scholar] [CrossRef]
- Cerný, M.; Rehák, P.; Umeno, Y.; Pokluda, J. Stability and strength of covalent crystals under uniaxial and triaxial loading from first principles. J. Phys. Condens. Matter 2013, 25, 35401–35408. [Google Scholar] [CrossRef] [PubMed]
- Sesták, P.; Friák, M.; Holec, D.; Vsianská, M.; Sob, M. Strength and brittleness of interfaces in Fe-Al superalloy nanocomposites under multiaxial loading: An ab initio and atomistic study. Nanomaterials 2018, 8, 873. [Google Scholar] [CrossRef]
- Umeno, Y.; Cerný, M. Effect of normal stress on the ideal shear strength in covalent crystals. Phys. Rev. B 2008, 77, 100101–100104. [Google Scholar] [CrossRef]
- Umeno, Y.; Cerný, M. Ideal shear strength under compression and tension in C, Si, Ge, and cubic SiC: An ab initio density functional theory study. J. Phys. Condens. Matter 2011, 23, 385401(1)–385401(7). [Google Scholar] [CrossRef]
- Cerný, M.; Rehák, P.; Pokluda, J. The origin of lattice instability in bcc tungsten under triaxial loading. Philos. Mag. 2017, 97, 2971–2984. [Google Scholar] [CrossRef]
- Baonza, V.G.; Cáceres, M.; Núñez, J. Universal compressibility behavior of dense phases. Phys. Rev. B 1995, 51, 28–37. [Google Scholar] [CrossRef]
- Francisco, E.; Bermejo, M.; García Baonza, V.; Gerward, L.; Recio, J.M. Spinodal equation of state for rutile TiO2. Phys. Rev. B 2003, 67, 064110(1)–064110(8). [Google Scholar] [CrossRef]
- Gonze, X.; Beuken, J.M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties: The ABINIT software project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1786–1799. [Google Scholar] [CrossRef] [PubMed]
- Ambrosetti, A.; Ferri, N.; Di Stasio, R.A., Jr.; Tkatchencko, A. Wavelike charge density fluctuations and van der Waals interactions in the nanoscale. Science 2016, 351, 1171–1176. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Hidden by graphene—Towards effective screening of interface van der Waals interactions vian monolayer coating. Carbon 2018, 139, 486–491. [Google Scholar] [CrossRef]
- Ambrosetti, A.; Silvestrelli, P.L. Faraday-like Screening by Two-Dimensional Nanomaterials: A Scale Dependent Tunable Effect. J. Phys. Chem. Lett. 2019, 10, 2044–2050. [Google Scholar] [CrossRef]
- Trouillier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef]
- Monkhost, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattice; Oxford Clarendon Press: London, UK, 1966. [Google Scholar]
- Zeina, M.J.; Servio, P.; Rey, A.D. Ideal Strength of Methane Hydrate and Ice Ih from First-Principles. Cryst. Growth. Des. 2015, 15, 5301–5309. [Google Scholar]
- Otero de la Roza, A.; Luaña, V. Runwien: A text-based interface for the WIEN package. Comput. Phys. Commun. 2009, 180, 800–812. [Google Scholar] [CrossRef]
- Baonza, V.G.; Taravillo, M.; Cáceres, M.; Núñez, J. Universal features of the equation of state of solids from a pseudospinodal hypothesis. Phys. Rev. B 1996, 53, 5252–5258. [Google Scholar] [CrossRef] [PubMed]
- Taravillo, M.; Baonza, V.G.; Núñez, J.; Cáceres, M. Simple equation of state for solids under compression. Phys. Rev. B 1996, 54, 7034–7045. [Google Scholar] [CrossRef] [PubMed]
- Baonza, V.G.; Cáceres, M.; Núñez, J. High-pressure compressibility behavior of liquids referred to a pseudospinodal curve. Chem. Phys. Lett. 1994, 228, 137–143. [Google Scholar] [CrossRef]
- Baonza, V.G.; Cáceres, M.; Núñez, J. Universal Behavior of Compressed Liquids. J. Chem. Phys. 1994, 19, 4955–4958. [Google Scholar] [CrossRef]
- Ogata, S.; Li, J.; Shibutant, N.; Yip, S. Ideal shear strain of metals and ceramics. Phys. Rev. B 2004, 70, 104104(1)–104104(7). [Google Scholar] [CrossRef]
- Brosh, E.; Makov, G.; Shneck, R.Z. The spinodal constraint on the equation of state of expanded fluids. J. Phys. Condens. Matter 2003, 19, 2991–3001. [Google Scholar] [CrossRef]
- Feldman, J.L. Elastic constants of 2H-MoS2 and 2H-NbSe2 extracted from measured dispersion curves and linear compressibilities. J. Phys. Chem. Solids 1976, 37, 1141–1144. [Google Scholar] [CrossRef]
- Karch, K.; Pavone, P.; Windl, W.; Schuelt, O.; Strauch, D. Ab initio calculation of structural and lattice-dynamical properties of silicon carbide. Phys. Rev. B 1994, 50, 17054–17063. [Google Scholar] [CrossRef]
- Umeno, Y.; Kubo, A.; Nagao, S. Density functional theory calculation of ideal strength of SiC and GaN: Effect of multi-axial stress. Comput. Mater. Sci. 2015, 109, 105–110. [Google Scholar] [CrossRef]
- Ioffeinstitut. 2003. Available online: http://www.ioffe.ru/SVA/NSM (accessed on 18 August 2019).
- Li, Z.; Brandt, R.C. The single-crystal elastic constants of cubic (3C) SiC to 1000 °C. J. Mater. Sci. 1987, 22, 2557–2559. [Google Scholar] [CrossRef]
- Saramasak, K.; Limpijumnong, S.; Lambrecht, W.R.L. First principles calculations of elastic properties under pressure in SiC. Comput. Mater. Sci. 2010, 49, S43–S46. [Google Scholar]
- Villard, P.; Calvert, L.D. Pearson’s Handbook of Crystallographic Data for intermetallic Phases; ASM international: Cleveland, OH, USA, 1991. [Google Scholar]
- Kamitani, K.; Grimsditch, M.; Nipko, J.C.; Loong, C.K.; Okada, M.; Kimura, I. The elastic constants of silicon carbide: A Brillouin-scattering study of 4H and 6H SiC single crystals. J. Appl. Phys. 1997, 82, 3152–3154. [Google Scholar] [CrossRef]
- Liu, F.; Ming, P.; Li, J. Ab initio calculation of ideal strength and phonon instability of graphene under tension. Phys. Rev. B 2007, 76, 064120(1)–064120(7). [Google Scholar] [CrossRef]
- Bosak, A.; Krisch, M.; Mohr, M.; Maultzsch, J.; Thomsen, C. Elasticity of single-crystalline graphite: Inelastic x-ray scattering study. Phys. Rev. B 2007, 75, 153408(1)–153408(4). [Google Scholar] [CrossRef]
- Ooi, N.; Rairkar, A.; Adams, J.B. Density functional study of graphite bulk and surface properties. Carbon 2006, 44, 231–242. [Google Scholar] [CrossRef]
- Mounet, N.; Marzari, N. First-principles determination of the structural, vibrational and thermodynamic properties of diamond, graphite, and derivatives. Phys. Rev. B 2005, 71, 205214(1)–205214(14). [Google Scholar] [CrossRef]
- Alexiev, V.; Prins, R.; Weber, T. Ab initio study of MoS2 and Li adsorbed on the (10-10) face of MoS2. Phys. Chem. Chem. Phys. 2000, 2, 1815–1827. [Google Scholar] [CrossRef]
- Fan, D.; Xu, J.; Ma, N.; Liu, J.; Xie, H. P-V-T Equation of state of molibdenite (MoS2) by a diamond anvil cell and in situ synchrotron angel-dispersive X-ray diffraction. Phys. B 2014, 451, 53–57. [Google Scholar] [CrossRef]
- Li, T. Ideal strength and phonon instability in single-layer MoS2. Phys. Rev. B 2012, 85, 235407(1)–235407(5). [Google Scholar] [CrossRef]
- Li, P.; Jiang, C.; Xu, S.; Zhuang, Y.; Gao, L.; Hu, A.; Wang, H.; Lu, Y. In situ nanomechanical characterization of multi-layer MoS2 membranes: from intraplanar to interplanar fracture. Nanoscale 2017, 9, 9119–9128. [Google Scholar] [CrossRef] [PubMed]
- Abbasi-Pérez, D.; Menéndez, J.M.; Recio, J.M.; Otero-de-la-Roza, A.; del Corro, E.; Taravillo, M.; Baonza, V.G.; Marqués, M. Modeling graphite under stress: Equations of state, vibrational modes, and interlayer friction. Phys. Rev. B 2014, 90, 054105(1)–054105(10). [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals; Oxford University Press: New York, NY, USA, 2004. [Google Scholar]
- Bertolazzi, S.; Brivio, J.; Kis, A. Stretching and Breaking of Ultrathin MoS2. ACS Nano 2011, 5, 9703–9709. [Google Scholar] [CrossRef]
- Lorenz, T.; Teich, D.; Joswig, J.O.; Seifert, G. Theoretical Study of the Mechanical Behavior of Individual TiS2 and MoS2 Nanotubes. J. Phys. Chem. C 2012, 116, 11714–11721. [Google Scholar] [CrossRef]
- Cooper, R.C.; Lee, C.; Marianetti, C.A.; Wei, X.; Hone, J.; Kysar, J.W. Nonlinear elastic behavior of two-dimensional molybdenum disulfide. Phys. Rev. B 2013, 87, 035423-1–035423-11. [Google Scholar] [CrossRef]



| Material | Direction | |||
|---|---|---|---|---|
| 3C-SiC | [100] | 0.29 | 0.35 | 90.5 |
| [110] | 0.49 | 0.30 | 52.3 | |
| [111] | 0.36 | 0.15 | 45.1 | |
| 2H-SiC | [001] | 0.36 | 0.15 | 44.9 |
| [100] | 0.46 | 0.29 | 58.0 | |
| [120] | 0.34 | 0.17 | 50.7 | |
| Graphite | [001] | 0.35 | 0.99 | 0.06 |
| [100] | 0.53 | 0.26 | 85.8 | |
| [120] | 0.37 | 0.11 | 78.3 | |
| 2H-MoS | [001] | 0.39 | 0.05 | 0.07 |
| [100] | 0.38 | 0.27 | 21.4 | |
| [120] | 0.46 | 0.20 | 14.2 |
| This Work | Calculated | Experimental | ||
|---|---|---|---|---|
| 3C-SiC | a(Å) | 4.39 | 4.34 [41], 4.38 [42] | 4.34 [43] |
| (GPa) | 341 | 390 [41], 385 [42] | 352 [44] | |
| (GPa) | 130 | 134 [41], 128 [42] | 140 [44] | |
| (GPa) | 224 | 253 [41], 264 [42] | 233 [44] | |
| (GPa) | 200 | 219, 213 | 211 | |
| 2H-SiC | a(Å) | 3.085 | 3.05 [45], 3.09 [42] | 3.076 [46] |
| c(Å) | 5.060 | 5.00 [45], 5.07 [42] | 5.224 [46] | |
| (GPa) | 528 | 541 [45], 536 [42] | 501 ± 4 [47] | |
| (GPa) | 112 | 117 [45], 78 [42] | 111 ± 5 [47] | |
| (GPa) | 565 | 586 [45], 573 [42] | 553 ± 4 [47] | |
| (GPa) | 52 | 61 [45], 31 [42] | 52 ± 9 [47] | |
| (GPa) | 156 | 162 [45], 164 [42] | 163 ± 4 [47] | |
| (GPa) | 228 | 238, 214 | 220 | |
| Graphite | a(Å) | 2.521 | 2.451 [48] | 2.464 [49] |
| c(Å) | 7.067 | 6.582 [50] | 6.712 [49] | |
| (GPa) | 892 | 1118 [51] | 1109 ± 16 [49] | |
| (GPa) | 163 | 235 [51] | 139 ± 36 [49] | |
| (GPa) | 31 | 29 [51] | 38.7 ± 7 [49] | |
| (GPa) | 5 | 8.5 [51] | 0 ± 3 [49] | |
| (GPa) | 6 | −2.8 [51] | 5 ± 3 [49] | |
| (GPa) | 240 | 307 | 281 | |
| 2H-MoS | a(Å) | 3.19 | 3.16 [52] | 3.163 [53] |
| c(Å) | 12.56 | 12.296 [52] | 12.341 [53] | |
| (GPa) | 220 | 218 [52] | 238 [40] | |
| (GPa) | 45 | 38 [52] | −54 [40] | |
| (GPa) | 40 | 35 [52] | 52 [40] | |
| (GPa) | 16 | 17 [52] | 23 [40] | |
| (GPa) | 26 | 15 [52] | 19 [40] | |
| (GPa) | 75 | 68 | 57 |
| Material | Direction | (0) (GPa) | (kJ/mol) |
|---|---|---|---|
| 3C-SiC | [100] | 396 | 219 |
| [110] | 407 | 110 | |
| [111] | 478 | 50 | |
| 2H-SiC | [001] | 481 | 50 |
| [100] | 437 | 142 | |
| [120] | 450 | 66 | |
| Graphite | [001] | 0.99 | <1 |
| [100] | 746 | 201 | |
| [120] | 746 | 113 | |
| 2H-MoS | [001] | 2.41 | <1 |
| [100] | 150 | 69 | |
| [120] | 140 | 153 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chorfi, H.; Lobato, Á.; Boudjada, F.; Salvadó, M.A.; Franco, R.; Baonza, V.G.; Recio, J.M. Computational Modeling of Tensile Stress Effects on the Structure and Stability of Prototypical Covalent and Layered Materials. Nanomaterials 2019, 9, 1483. https://doi.org/10.3390/nano9101483
Chorfi H, Lobato Á, Boudjada F, Salvadó MA, Franco R, Baonza VG, Recio JM. Computational Modeling of Tensile Stress Effects on the Structure and Stability of Prototypical Covalent and Layered Materials. Nanomaterials. 2019; 9(10):1483. https://doi.org/10.3390/nano9101483
Chicago/Turabian StyleChorfi, Hocine, Álvaro Lobato, Fahima Boudjada, Miguel A. Salvadó, Ruth Franco, Valentín G. Baonza, and J. Manuel Recio. 2019. "Computational Modeling of Tensile Stress Effects on the Structure and Stability of Prototypical Covalent and Layered Materials" Nanomaterials 9, no. 10: 1483. https://doi.org/10.3390/nano9101483
APA StyleChorfi, H., Lobato, Á., Boudjada, F., Salvadó, M. A., Franco, R., Baonza, V. G., & Recio, J. M. (2019). Computational Modeling of Tensile Stress Effects on the Structure and Stability of Prototypical Covalent and Layered Materials. Nanomaterials, 9(10), 1483. https://doi.org/10.3390/nano9101483