1. Introduction
Society is increasingly aware of the usage of sustainable energy sources that protect the environment, such as renewable energy resources, whose viability is demonstrated. At the same time, it is necessary that energy storage devices also meet the same requirements of sustainability and efficiency, making the entire process of generation and consumption of energy as clean as possible. Nanotechnology has become one of the main subjects in science nowadays, offering exciting new possibilities in the field of renewable energy production/conversion and storage. An energy storage device is characterized by two main magnitudes. The first one is the energy density, which gives an account of the total energy that the device could store. The other magnitude refers to the time necessary for the device to store or supply a certain amount of energy to attend to the demand, which is known as power density.
Within storage systems, capacitors are those that have higher power densities, but the lowest energy density. Supercapacitors, apart from maintaining the power density of the usual capacitors, are able to reach higher energy density values of about one or two orders of magnitude above those achieved by usual energy storage devices. Therefore, by improving the energy storage capacity of these capacitors, devices with good performance both in autonomy and power density can be obtained, which present a wide range of applications in industry, electronics, or inclusively in means of transport [
1,
2]. Specifically, supercapacitors have direct application in those electrical systems that demand high power supply in short times, such as the engine of an electric car during vehicle acceleration. Another possible application would be the supply of extra power to the electricity network in specific periods of peak energy demand, which would tackle one of the main disadvantages of renewable energy. In addition, supercapacitors are small gadgets, so it would be possible to introduce this type of device into electronic circuits, causing capacitors to become increasingly smaller and improving their performance due to their high capacitance. Capacitors are usually classified into two types: electrolytic or electrostatic. For the first type, electric charge storage is produced by electrochemical processes. However, the electrolytic acid medium limits the lifespan of these devices as they end up being depleted or even oxidizing the capacitor’s own electrodes, rending it out of service. In addition, these devices have a great disadvantage regarding their ecological footprint, because at the end of their lifetime, they generate non-usable chemical residues. On the other hand, the storage of electrical charge on electrostatic capacitors occurs by the electric polarization of an insulating or dielectric material, when a voltage is applied between the conductive electrodes of the capacitor. From the environmental point of view, their advantages over electrolytic batteries or capacitors are clear: a longer (or even unlimited) lifetime and the non-generation of chemical waste at the end of its working time.
In recent years, several investigations based on nanotechnology have achieved important improvements in energy storage capacity of electrostatic capacitors [
3,
4]. Manufacturing of devices with high storage capacities and energy densities of up to 4 Wh/kg has been demonstrated [
5,
6], while maintaining the high power density characteristic of electrostatic capacitors. This type of device is called a super-electrostatic nanostructured capacitor (super-ENC) [
7]. The use of nanoporous anodic alumina membranes (NAAMs) as a patterned support for the manufacture of super-ENCs that is proposed in this work is a widely contrasted technique that offers good results not only for the manufacturing of electrostatic capacitors [
8], but also for other types of energy storage devices [
9,
10].
Equation (1) summarizes the main factors to be taken into account when evaluating the storage capacity of an electrostatic capacitor, where
C is the capacitance, ε
0 the dielectric permittivity of the vacuum, ε
r the relative permittivity of the dielectric medium of the capacitor, and
d is the thickness of such medium. Despite the apparent simplicity of this expression, it can be considered as an approximation to estimate the order of magnitude for a super-ENC’s capacitance. As shown in Equation (1), the capacitance is enhanced by a larger surface area (
S) of the electrodes. In order to increase the parameter by sizing up the dimensions of the device, NAAMs are used as a substrate, as they offer a high open surface area. By using electrochemical anodization techniques, it is possible to grow hexagonally self-ordered pores whose geometrical parameters can be properly tuned, thus obtaining a highly ordered nanoporous surface with well-defined dimensions, grown on the starting aluminum substrate. The atomic layer deposition (ALD) technique represents an important tool within the nanomaterials additive manufacturing owing to its enhanced possibilities like the fabrication of thin oxide films over micro- or mesoporous surfaces by covering them conformally [
11]. The use of the ALD technique allows one to take advantage of the internal surface inside the NAAM’s pores to deposit the three layers that make up the typical structure of the capacitor, that is, the upper and the lower electrode and, between them, the dielectric material. The goal of ALD employment is to reduce the thickness of the dielectric material (
d) to the order of nanometers, which results in a consequent increase of capacitance (see Equation (1)). This technique allows one to make coatings of oxide materials over porous substrates, achieving the deposition of layers with thicknesses in the range of nanometers on the internal surface of the nanopores [
11,
12]. Through ALD performance, it is possible to guarantee a uniform thickness substrate coating [
13,
14], able to be carried out on porous surfaces with diverse morphologies, whether they are micro-, meso-, or macroporous substrates [
15]. Within the storage of energy, ALD is a widespread technique and has a wide range of applications depending on the substrate on which the ALD is made, from the treatment of porous carbon to form a cathodic material that can be implemented with batteries [
16], to the coating of ZnO nanowires as electrostatic capacitors [
17]. This technique is also used to form supercapacitor devices over multiple substrates. There is a detailed study that applies ALD on NAAMs [
4,
5,
6,
7] in a very similar way to what was conducted in this work, developing new electrostatic supercapacitor devices, in which ALD becomes essential in the conformation of its electrodes and dielectric material. However, its range of application goes further, as ALD has been successfully used in recent years for electrochemical capacitor manufacturing over bundles of carbon nanotubes (CNT) [
18,
19], or TiO
2 nanoparticles [
20]. One of the main advantages provided by ALD is the performance of electrodes with greater mechanical and chemical stability, owing to the deposition of conformal coatings, which are adapted, in many cases, in the form of nanowires [
21,
22].
In this work, the manufacturing process of electrostatic supercapacitors by combining the ALD technique and electrochemical anodization of nanoporous anodic alumina templates as starting substrates is reported. The so-formed electrostatic capacitor structure, which consists of a top electrode, a dielectric material, and finally a bottom electrode, has been reduced to nanoscale dimensions by depositing the required materials over patterned nanoporous anodic alumina membranes using the ALD technique. A thin layer of aluminum-doped zinc oxide, 6 nm in thickness, is used as both the top and bottom electrodes’ material, while two different dielectric materials were tested. On the one hand, a triple-layer made by successive combination of a 3 nm in thickness for each layer of silicon dioxide (SiO2), plus titanium dioxide (TiO2), and silicon dioxide (SiO2) again, forming the three-layered SiO2/TiO2/SiO2 dielectric medium, and on the other hand, a single layer with 9 nm in thickness made of alumina (Al2O3).
Regarding the selection of dielectric materials, two criteria have been taken into account. Firstly, the material needs to have a high relative permittivity in order to increase the capacitance. The second criterion is related to the energy gap between its valence and conduction bands, which should be as high as possible, to avoid leakage currents and to reach the maximum working voltage of the capacitor. Among the different insulating materials characterized in the work of [
23], the one with the highest relative permittivity (TiO
2) and the one with the largest gap (SiO
2) are extracted. Unfortunately, these two properties are opposed, with TiO
2 being the material with the lowest gap, and SiO
2 being the dielectric with the lowest permittivity, as can be seen in
Table 1. For this reason, in this work, the combination of these two materials in a triple layer of SiO
2/TiO
2/SiO
2 dielectric is proposed, in such a way that this new material can provide the high performance of permittivity and insulation that TiO
2 and SiO
2 display by themselves. The electrical behavior of this new multilayered capacitor is compared with the performance of a single layer capacitor, which is conformed by Al
2O
3 as the dielectric layer. This last dielectric is a material whose ALD deposition has been widely characterized [
4,
5,
6,
11,
14,
24,
25], and which also exhibits an intermediate permittivity and band gap values with respect to TiO
2 and SiO
2.
Both oxide materials (Al2O3 and SiO2/TiO2/SiO2) have 9 nm in total thickness and play the role of insulating layers of the capacitors. The electrical properties of these capacitors were tested under different experimental configurations, by measuring characteristic magnitudes such as the impedance and capacitance on the AC and DC frequency regime. In order to give a complete overview on the electrical behavior of these capacitors, breakdown voltage values along with leakage currents are also studied. This demonstrated the ability of using nanostructured materials for designing energy storage supercapacitor devices.
5. Conclusions
This work has faced the development of electrostatic capacitors and its enhanced possibilities by using nanomaterials, in this way covering the full manufacturing and characterization process of these energy storage devices. An innovative fabrication method has been proposed and achieved, based on the successive combination of an ultrathin layered nanomaterial for the conformation of the dielectric medium of the capacitors. Likewise, an experimental procedure has been followed for the complete characterization of these devices, consisting of three phases, from which the intrinsic magnitudes that completely characterize a capacitor can be measured, such as internal resistance, leakage resistance, capacitance, and breakdown voltage. The test of the manufactured devices in a real circuit, including a model to explain their electrical behavior, which is the main novelty of this study, has obtained experimental results confirming the validity of such a model.
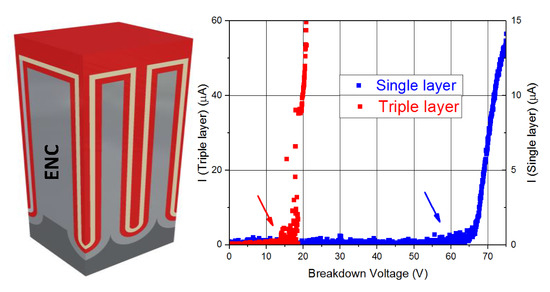
It has been found that the Al2O3 single-dielectric layer capacitors of 9 nm in thickness have been shown to exhibit a better performance than the triple dielectric layer capacitors composed of SiO2/TiO2/SiO2 sheets, each 3 nm in thickness. In particular, single dielectric layer capacitors have less internal resistance (2.3 kΩ), so they are more favorable for storage applications because of a consequent lower power consumption. Al2O3 single-layered capacitors also offer a higher capacitance in dynamic regime (41.6 nF) than those of triple-layered SiO2/TiO2/SiO2. Furthermore, the former display leakage current is lower than 50 nA, so it guarantees that the current losses will be minimal. The main advantage shown by these capacitors is the high value of breakdown voltage (63 V), as a higher working voltage greatly improves the storage capacity of electrical energy of these devices. Only the static regime of capacitance for triple dielectric layer capacitors (93 nF) is higher than that of the single dielectric layer devices (54 nF). However, taking into account all the features in which the Al2O3 capacitors offer better performance, a single property is not enough to affirm that SiO2/TiO2/SiO2 devices have better characteristics.
Nevertheless, the capacitance values derived from our electrostatic supercapacitor prototype are not as high as expected. The values obtained are coherent with the performed analysis, as both the dynamic and the static procedures yield values of the same order of magnitude (nF). However, they are far from the expected capacitance values in the μF range theoretically predicted for these kind of devices, so certain aspects of the manufacture of the supercapacitor devices should be further reconsidered. A feasible explanation on the discrepancies between the expected values of capacities and the experimentally measured ones is that the AZO layer is not properly fulfilling its function as electrode material, for either of two reasons. The first one is that the contact to the AZO layer with silver paint would not be appropriate and thus there is no electron transfer between the AZO layer and the conductive silver paint. The second reason would be that the AZO layer itself is a semiconducting material, and hence it is not able to efficiently conduct the electrical current along the channels of the pores. In addition, the design of the electrical connections of the device becomes critical, because current leakages and short circuits between the electrodes need to be avoided. For example, leakage currents may be decreased in the case of triple layer capacitors, whether or not it can be guaranteed that the electrodes are completely isolated to achieve the most desirable device performance.
There are, therefore, two ways of improving the super-ENCs’ capacitance. On the one hand, the substitution of the AZO layer by using a better conductive material that fits the cylindrical morphology of the pores, such as carbon nanotubes, thus taking advantage of the internal surface of the NAAM to increase the capacitance of the devices. On the other hand, the use of more refined techniques to contact the electrodes, such as wire bonding, would allow precise delimitation of the contact zones, avoiding regions in which short circuits could occur, thus reducing the presence of leakage currents. These advances would significantly improve the performance of the manufactured prototypes that, according to the reported results, could become in very promising energy storage devices. In fact, the super-ENCs are suitable complements for the batteries of electrical systems such as vehicles or electricity supply domestic networks. Besides having a high energy density and faster response under a specific power demand, they also present an environmentally sustainable alternative to the current polluting energy supply systems.